28.3二次函数与实际问题+课件2023-2024学年数学人教版(五四制)九年级上册(18张PPT)
文档属性
| 名称 | 28.3二次函数与实际问题+课件2023-2024学年数学人教版(五四制)九年级上册(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 424.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
28.3二次函数与实际问题
教学目标:
我能利用二次函数的有关知识,解决抛物线型问题.
我能将实际问题转化为二次函数问题,进而建立数学模型,体会数学建模的思想.
从地面竖直向上抛出一小球,小球的高度 h(单位:
m)与小球的运动时间 t(单位:s)之间的关系式是
h= 30t - 5t 2 (0≤t≤6).小球的运动时间是多少时,小
球最高?小球运动中的最大高度是多少?
1.创设情境,引出问题
小球运动的时间是 3 s 时,小球最高.
小球运动中的最大高度是 45 m.
2.结合问题,拓展一般
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
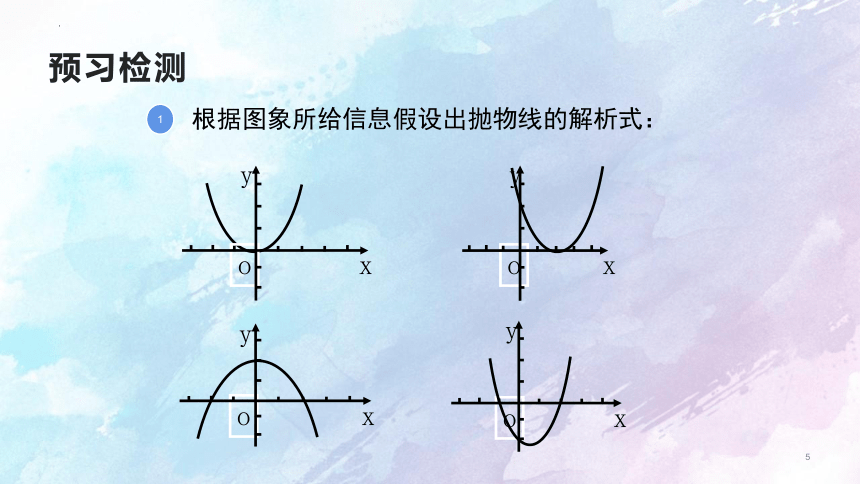
预习检测
5
根据图象所给信息假设出抛物线的解析式:
1
o
x
y
o
x
y
o
x
y
o
x
y
新知探究
6
图中是抛物线型拱桥,当拱顶离水面 2米时,水面宽4米。水面下降1米,水面宽度增加多少?
1
新知探究
7
如何建立直角坐标系?
2
A
B
C
D
E
图中是抛物线型拱桥,当拱顶离水面 2米时,水面宽4米。水面下降1米,水面宽度增加多少?
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
y
y
y
y
o
o
o
o
x
x
x
x
你有其他建立平面直角坐标系的方法吗?
1
3
4
变式探究
9
当拱顶离水面 2米时,水面宽4米。一艘露出水面部分高1米,宽2.6米的小船能否安全从桥下通过?
3
y
x
-2
2
-2
归纳小结
10
解
求
建
得
建立适当的平面直角坐标系.
从已知条件中获得所需条件
利用待定系数法求出解析式.
利用已求的解析式解决问题.
建立二次函数模型解决抛物线型问题的一般步骤:
回归情景
11
方硕跳起投篮,如图2,已知球在A处出手时离地面20/9 m,与篮筐中心C的水平距离是7m,当球运行的水平距离是4 m时,达到最大高度4m(B处),设篮球运行的路线为抛物线.篮筐距地面3m.
问:此球能否投中
4
能力提升
12
y
x
o
3.类比引入,探究问题
整理后得
用总长为 60 m 的篱笆围成矩形场地,矩形面积 S
随矩形一边长 l 的变化而变化.当 l 是多少米时,场地
的面积 S 最大?
解: ,
∴ 当 时,
S 有最大值为 .
当 l 是 15 m 时,场地的面积 S 最大.
(0<l<30).
( )
( )
4.归纳探究,总结方法
2.列出二次函数的解析式,并根据自变量的实际
意义,确定自变量的取值范围.
3.在自变量的取值范围内,求出二次函数的最大
值或最小值.
1.由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
5.课堂练习
为了改善小区环境,某小区决定要在一块一边靠墙
(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿
化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如
下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y
m 2.
(1)求 y 与 x 之间的函数关系
式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件
的绿化带的面积最大?
D
C
B
A
25 m
某农场主计划建一个养鸡场,为节约材料,鸡场一边靠着一堵墙(墙足够长),另三边用40米竹篱笆围成,现有两种方案无法定夺: ①围成一个矩形;②围成一个半圆形.设矩形的面积为 平方米,半圆形的面积为 平方米 ,半径为r米。请你通过计算帮农场主选择一个围成区域最大的方案(π取3)
x
(1) 如何求二次函数的最小(大)值,并利用其
解决实际问题?
(2) 在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
6.课堂小结
再见
28.3二次函数与实际问题
教学目标:
我能利用二次函数的有关知识,解决抛物线型问题.
我能将实际问题转化为二次函数问题,进而建立数学模型,体会数学建模的思想.
从地面竖直向上抛出一小球,小球的高度 h(单位:
m)与小球的运动时间 t(单位:s)之间的关系式是
h= 30t - 5t 2 (0≤t≤6).小球的运动时间是多少时,小
球最高?小球运动中的最大高度是多少?
1.创设情境,引出问题
小球运动的时间是 3 s 时,小球最高.
小球运动中的最大高度是 45 m.
2.结合问题,拓展一般
由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,
当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
如何求出二次函数 y = ax 2 + bx + c 的最小(大)值?
预习检测
5
根据图象所给信息假设出抛物线的解析式:
1
o
x
y
o
x
y
o
x
y
o
x
y
新知探究
6
图中是抛物线型拱桥,当拱顶离水面 2米时,水面宽4米。水面下降1米,水面宽度增加多少?
1
新知探究
7
如何建立直角坐标系?
2
A
B
C
D
E
图中是抛物线型拱桥,当拱顶离水面 2米时,水面宽4米。水面下降1米,水面宽度增加多少?
(0,0)
(4,0)
(2,2)
(-2,-2)
(2,-2)
(0,0)
(-2,0)
(2,0)
(0,2)
(-4,0)
(0,0)
(-2,2)
y
y
y
y
o
o
o
o
x
x
x
x
你有其他建立平面直角坐标系的方法吗?
1
3
4
变式探究
9
当拱顶离水面 2米时,水面宽4米。一艘露出水面部分高1米,宽2.6米的小船能否安全从桥下通过?
3
y
x
-2
2
-2
归纳小结
10
解
求
建
得
建立适当的平面直角坐标系.
从已知条件中获得所需条件
利用待定系数法求出解析式.
利用已求的解析式解决问题.
建立二次函数模型解决抛物线型问题的一般步骤:
回归情景
11
方硕跳起投篮,如图2,已知球在A处出手时离地面20/9 m,与篮筐中心C的水平距离是7m,当球运行的水平距离是4 m时,达到最大高度4m(B处),设篮球运行的路线为抛物线.篮筐距地面3m.
问:此球能否投中
4
能力提升
12
y
x
o
3.类比引入,探究问题
整理后得
用总长为 60 m 的篱笆围成矩形场地,矩形面积 S
随矩形一边长 l 的变化而变化.当 l 是多少米时,场地
的面积 S 最大?
解: ,
∴ 当 时,
S 有最大值为 .
当 l 是 15 m 时,场地的面积 S 最大.
(0<l<30).
( )
( )
4.归纳探究,总结方法
2.列出二次函数的解析式,并根据自变量的实际
意义,确定自变量的取值范围.
3.在自变量的取值范围内,求出二次函数的最大
值或最小值.
1.由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,当
时,二次函数 y = ax 2 + bx + c 有最小(大) 值
5.课堂练习
为了改善小区环境,某小区决定要在一块一边靠墙
(墙长 25 m)的空地上修建一个矩形绿化带 ABCD,绿
化带一边靠墙, 另三边用总长为 40 m 的栅栏围住 (如
下图).设绿化带的 BC 边长为 x m,绿化带的面积为 y
m 2.
(1)求 y 与 x 之间的函数关系
式,并写出自变量 x 的取值范围.
(2)当 x 为何值时,满足条件
的绿化带的面积最大?
D
C
B
A
25 m
某农场主计划建一个养鸡场,为节约材料,鸡场一边靠着一堵墙(墙足够长),另三边用40米竹篱笆围成,现有两种方案无法定夺: ①围成一个矩形;②围成一个半圆形.设矩形的面积为 平方米,半圆形的面积为 平方米 ,半径为r米。请你通过计算帮农场主选择一个围成区域最大的方案(π取3)
x
(1) 如何求二次函数的最小(大)值,并利用其
解决实际问题?
(2) 在解决问题的过程中应注意哪些问题?你学到了哪些思考问题的方法?
6.课堂小结
再见
