13.1轴对称 同步练习(含答案) 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 13.1轴对称 同步练习(含答案) 2023—2024学年人教版数学八年级上册 | 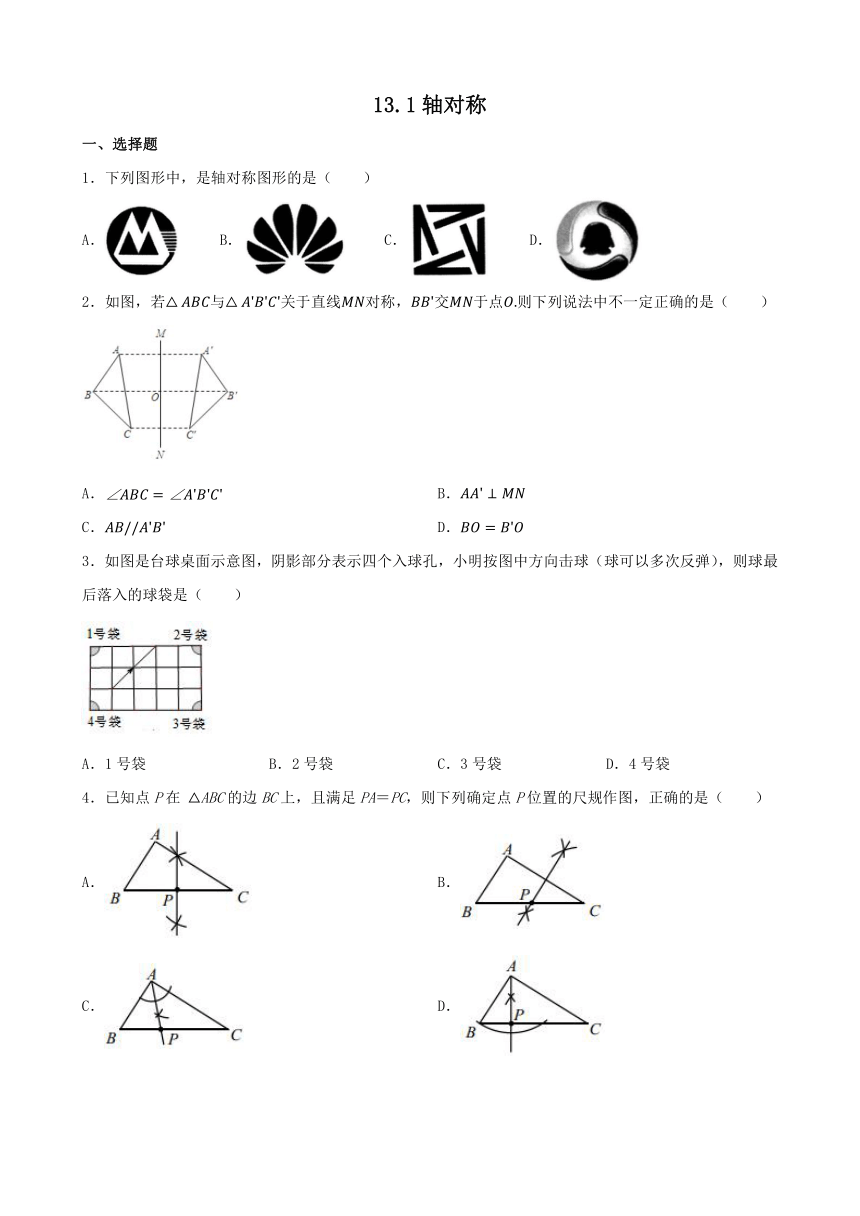 | |
| 格式 | docx | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 12:25:17 | ||
图片预览


文档简介
13.1轴对称
一、选择题
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.如图,若与关于直线对称,交于点则下列说法中不一定正确的是( )
A. B.
C. D.
3.如图是台球桌面示意图,阴影部分表示四个入球孔,小明按图中方向击球(球可以多次反弹),则球最后落入的球袋是( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋
4.已知点P在 ABC的边BC上,且满足PA=PC,则下列确定点P位置的尺规作图,正确的是( )
A. B.
C. D.
5.如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于点M,交OB于点N,若△PMN的周长为10,则P1P2的值是( )
A.6 B.8 C.10 D.12
6.如图,点P在锐角 的内部,连接 , ,点P关于 、 所在直线的对称点分别是 、 ,则 、 两点之间的距离可能是( )
A.8 B.7 C.6 D.5
7.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=6,CF=2,则AC的长度为( )
A.6 B.7 C.8 D.9
8.如图,在中,AE的垂直平分线MN交BE于点C,连接AC.若,,,则的周长等于( )
A.11 B.16 C.17 D.18
二、填空题
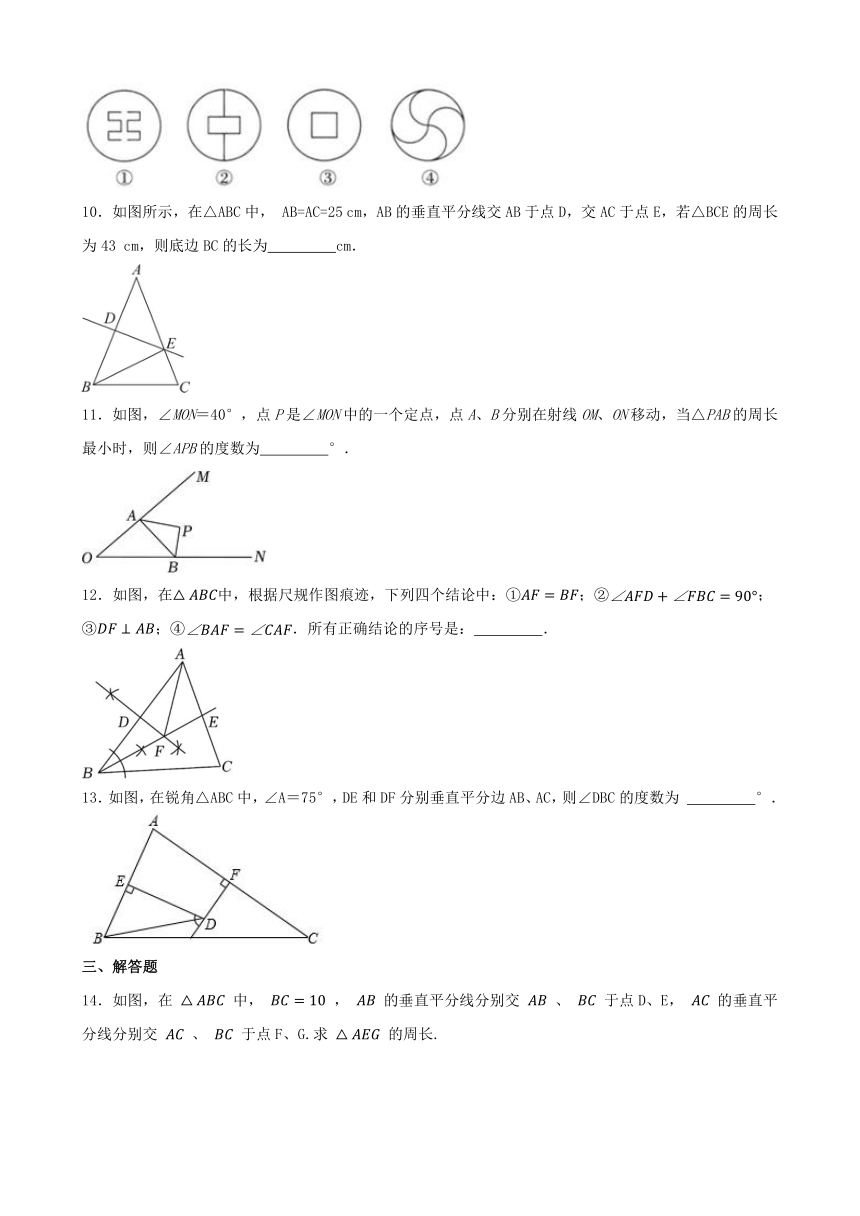
9.如图,是轴对称图形且只有两条对称轴的是 (填序号).
10.如图所示,在△ABC中, AB=AC=25 cm,AB的垂直平分线交AB于点D,交AC于点E,若△BCE的周长为43 cm,则底边BC的长为 cm.
11.如图,∠MON=40°,点P是∠MON中的一个定点,点A、B分别在射线OM、ON移动,当△PAB的周长最小时,则∠APB的度数为 °.
12.如图,在中,根据尺规作图痕迹,下列四个结论中:①;②;③;④.所有正确结论的序号是: .
13.如图,在锐角△ABC中,∠A=75°,DE和DF分别垂直平分边AB、AC,则∠DBC的度数为 °.
三、解答题
14.如图,在 中, , 的垂直平分线分别交 、 于点D、E, 的垂直平分线分别交 、 于点F、G.求 的周长.
15.如图, 在平面直角坐标系中, , , .
(1) 与 关于 轴对称,请画出 ,并写出点 , , 的坐标;
(2)求 的面积.
16.如图,在直角坐标系中,△ABC的三个顶点都在坐标轴上,A,B两点关于y轴对称,点C是y轴正半轴上一个动点,AD是角平分线.
(1)如图1,若∠ACB=90°,直接写出线段AB,CD,AC之间数量关系;
(2)如图2,若AB=AC+BD,求∠ACB的度数.
参考答案
1.B
2.C
3.B
4.B
5.C
6.D
7.C
8.B
9.①②
10.18
11.100
12.①②③
13.15
14.解:∵ 是 的垂直平分线,
∴ ,
∵ 是 的垂直平分线,
∴ ,
∴ 的周长 .
15.(1)解:作 ,
, , ;
(2)解: ,
,
.
16.(1)解:AB=AC+CD;
理由如下:如图1,过D作DM⊥AB于M,
∵A,B两点关于y轴对称,
∴CA=CB,
∵∠ACB=90°,AD平分∠CAB,
∴CD=MD,∠ABC=45°,
∴∠BDM=45°,
∴BM=DM,
∴BM=CD,
在Rt△ADC和Rt△ADM中,
,
∴Rt△ADC≌Rt△ADM(HL),
∴AC=AM,
∴AB=AM+BM=AC+CD,
即AB=AC+CD;
(2)解:设∠ACB=x,则∠CAB=∠CBA=90°﹣ ,
在AB上截取AK=AC,连结DK,
∵AB=AC+BD,
∴BK=BD,
∵AD是角平分线,
∴∠CAD=∠DAB,
在△CAD和△KAD中,
,
∴△CAD≌△KAD(SAS),
∴∠ACD=∠AKD=x,
∴∠BKD=180°﹣x,
∵BK=BD,
∴∠BDK=180°﹣x,
在△BDK中,
180°﹣x+180°﹣x+90°﹣ =180°
∴x=108°,
∴∠ACB=108°.
一、选择题
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.如图,若与关于直线对称,交于点则下列说法中不一定正确的是( )
A. B.
C. D.
3.如图是台球桌面示意图,阴影部分表示四个入球孔,小明按图中方向击球(球可以多次反弹),则球最后落入的球袋是( )
A.1号袋 B.2号袋 C.3号袋 D.4号袋
4.已知点P在 ABC的边BC上,且满足PA=PC,则下列确定点P位置的尺规作图,正确的是( )
A. B.
C. D.
5.如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于点M,交OB于点N,若△PMN的周长为10,则P1P2的值是( )
A.6 B.8 C.10 D.12
6.如图,点P在锐角 的内部,连接 , ,点P关于 、 所在直线的对称点分别是 、 ,则 、 两点之间的距离可能是( )
A.8 B.7 C.6 D.5
7.如图,△ABC中,EF是AB的垂直平分线,与AB交于点D,BF=6,CF=2,则AC的长度为( )
A.6 B.7 C.8 D.9
8.如图,在中,AE的垂直平分线MN交BE于点C,连接AC.若,,,则的周长等于( )
A.11 B.16 C.17 D.18
二、填空题
9.如图,是轴对称图形且只有两条对称轴的是 (填序号).
10.如图所示,在△ABC中, AB=AC=25 cm,AB的垂直平分线交AB于点D,交AC于点E,若△BCE的周长为43 cm,则底边BC的长为 cm.
11.如图,∠MON=40°,点P是∠MON中的一个定点,点A、B分别在射线OM、ON移动,当△PAB的周长最小时,则∠APB的度数为 °.
12.如图,在中,根据尺规作图痕迹,下列四个结论中:①;②;③;④.所有正确结论的序号是: .
13.如图,在锐角△ABC中,∠A=75°,DE和DF分别垂直平分边AB、AC,则∠DBC的度数为 °.
三、解答题
14.如图,在 中, , 的垂直平分线分别交 、 于点D、E, 的垂直平分线分别交 、 于点F、G.求 的周长.
15.如图, 在平面直角坐标系中, , , .
(1) 与 关于 轴对称,请画出 ,并写出点 , , 的坐标;
(2)求 的面积.
16.如图,在直角坐标系中,△ABC的三个顶点都在坐标轴上,A,B两点关于y轴对称,点C是y轴正半轴上一个动点,AD是角平分线.
(1)如图1,若∠ACB=90°,直接写出线段AB,CD,AC之间数量关系;
(2)如图2,若AB=AC+BD,求∠ACB的度数.
参考答案
1.B
2.C
3.B
4.B
5.C
6.D
7.C
8.B
9.①②
10.18
11.100
12.①②③
13.15
14.解:∵ 是 的垂直平分线,
∴ ,
∵ 是 的垂直平分线,
∴ ,
∴ 的周长 .
15.(1)解:作 ,
, , ;
(2)解: ,
,
.
16.(1)解:AB=AC+CD;
理由如下:如图1,过D作DM⊥AB于M,
∵A,B两点关于y轴对称,
∴CA=CB,
∵∠ACB=90°,AD平分∠CAB,
∴CD=MD,∠ABC=45°,
∴∠BDM=45°,
∴BM=DM,
∴BM=CD,
在Rt△ADC和Rt△ADM中,
,
∴Rt△ADC≌Rt△ADM(HL),
∴AC=AM,
∴AB=AM+BM=AC+CD,
即AB=AC+CD;
(2)解:设∠ACB=x,则∠CAB=∠CBA=90°﹣ ,
在AB上截取AK=AC,连结DK,
∵AB=AC+BD,
∴BK=BD,
∵AD是角平分线,
∴∠CAD=∠DAB,
在△CAD和△KAD中,
,
∴△CAD≌△KAD(SAS),
∴∠ACD=∠AKD=x,
∴∠BKD=180°﹣x,
∵BK=BD,
∴∠BDK=180°﹣x,
在△BDK中,
180°﹣x+180°﹣x+90°﹣ =180°
∴x=108°,
∴∠ACB=108°.
