第十一章 三角形 单元练习(含答案) 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 第十一章 三角形 单元练习(含答案) 2023—2024学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 115.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 12:27:56 | ||
图片预览

文档简介
第十一章 三角形
一、选择题
1.下列各组数可作为一个三角形三边长的是( )
A.1,2,4 B.4,5,9 C.4,6,9 D.5,5,11
2.如图,△ABC中,AC边上的高是( )
A.线段CD B.线段AF C.线段BE D.线段CE
3.如图,工人师傅砌门时,常用木条 固定长方形门框 ,使其不变形,这样做的根据是( )
A.两点之间,线段最短 B.直角三角形的两个锐角互余
C.三角形三个内角和等于 D.三角形具有稳定性
4.在 中,若 , ,则 的度数为( )
A.65° B.70° C.75° D.80°
5.一副三角板,按如图所示叠放在一起,则图中∠α的度数为( )
A.10° B.15° C.20° D.25°
6.如图,AD、BE分别是△ABC的角平分线和高线,若∠ABE=26°,则∠CAD的度数为( )
A.32° B.35° C.37° D.64°
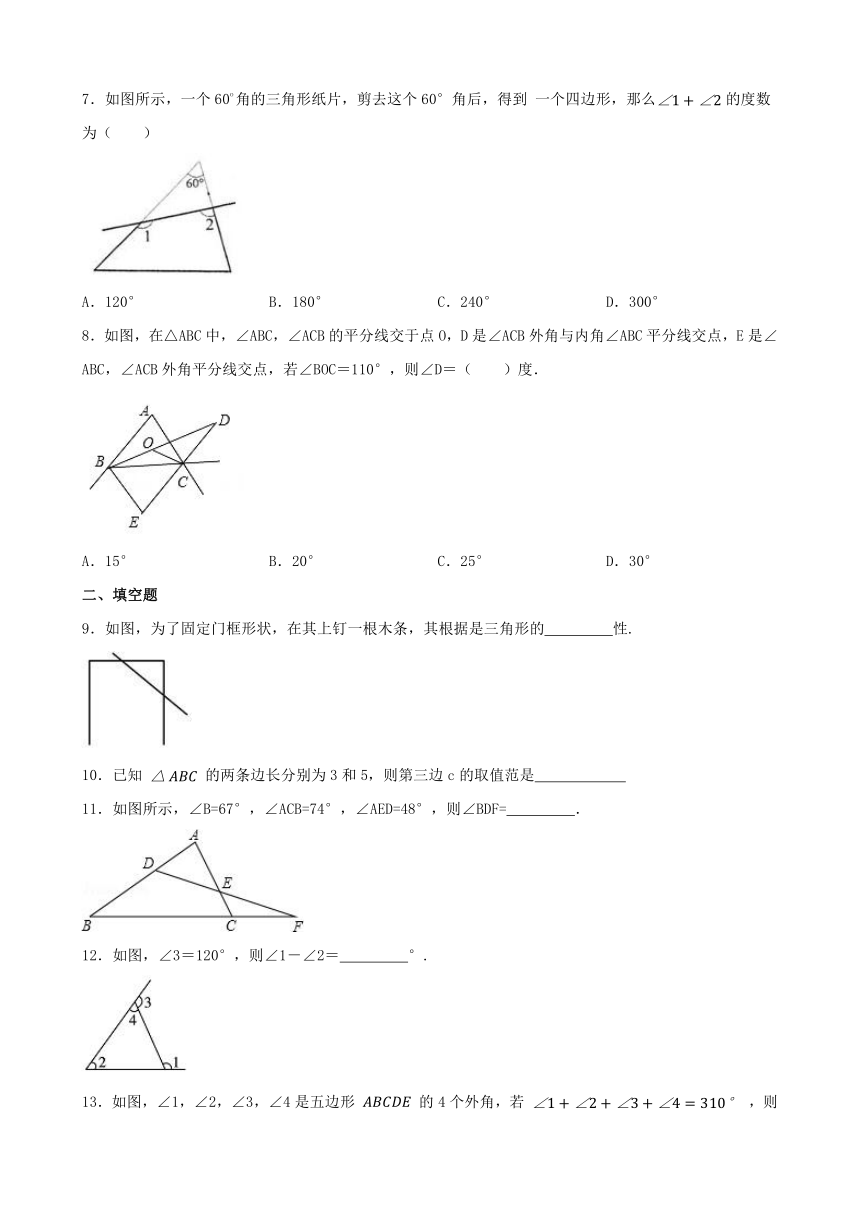
7.如图所示,一个60o角的三角形纸片,剪去这个60°角后,得到 一个四边形,那么的度数为( )
A.120° B.180° C.240° D.300°
8.如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角与内角∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点,若∠BOC=110°,则∠D=( )度.
A.15° B.20° C.25° D.30°
二、填空题
9.如图,为了固定门框形状,在其上钉一根木条,其根据是三角形的 性.
10.已知 的两条边长分别为3和5,则第三边c的取值范是
11.如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF= .
12.如图,∠3=120°,则∠1-∠2= °.
13.如图,∠1,∠2,∠3,∠4是五边形 的4个外角,若 ,则
的度数为 .
三、解答题
14.已知三角形三边长分别为a、b、c,其中a、b满足(a﹣6)2+|b﹣8|=0,求这个三角形最长边c的取值范围.
15.一个多边形的内角和比外角和的 多 ,它是几边形?
16.如图,在△ABC中,∠ABC、∠ACB的平分线BE,CD相交于点F,已知∠ABC=40°,∠A=60°,求∠BFD的度数.
17.如图,在 中, 为 的高, 为 的角平分线, 交 于点G, , ,求 的大小.
18.如图,已知中,是边上的高,平分,与相交于点P,,,求和的度数.
参考答案
1.C
2.C
3.D
4.A
5.B
6.A
7.C
8.B
9.稳定
10.2<c<8
11.87°
12.60
13.130°
14.解:∵(a﹣6)2+|b﹣8|=0,∴a﹣6=0,b﹣8=0,∴a=6,b=8,b﹣a<c<a+b,这个三角形的最长边c,c>b=8,8<c<14
15.解:设这个多边形边数为 ,依题意得:
,
解得: ,
答:它是七边形
16.解:∵∠A=60°
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∵∠ABC,∠ACB的平分线BE,CD相交于点F,
∴∠FBC+∠FCB= ∠ABC+ ∠ACB= (∠ABC+∠ACB)=60°,
∵∠BFD=∠FBC+∠FCB,
∴∠BFD=60°.
17.解: 为 的高,
.
.
在 △ABE 中, .
为 的角平分线,
.
.
18.解:∵是边上的高,
∴,
在中,,
∴,
∵平分,
∴,
∵是的外角,
∴.
一、选择题
1.下列各组数可作为一个三角形三边长的是( )
A.1,2,4 B.4,5,9 C.4,6,9 D.5,5,11
2.如图,△ABC中,AC边上的高是( )
A.线段CD B.线段AF C.线段BE D.线段CE
3.如图,工人师傅砌门时,常用木条 固定长方形门框 ,使其不变形,这样做的根据是( )
A.两点之间,线段最短 B.直角三角形的两个锐角互余
C.三角形三个内角和等于 D.三角形具有稳定性
4.在 中,若 , ,则 的度数为( )
A.65° B.70° C.75° D.80°
5.一副三角板,按如图所示叠放在一起,则图中∠α的度数为( )
A.10° B.15° C.20° D.25°
6.如图,AD、BE分别是△ABC的角平分线和高线,若∠ABE=26°,则∠CAD的度数为( )
A.32° B.35° C.37° D.64°
7.如图所示,一个60o角的三角形纸片,剪去这个60°角后,得到 一个四边形,那么的度数为( )
A.120° B.180° C.240° D.300°
8.如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACB外角与内角∠ABC平分线交点,E是∠ABC,∠ACB外角平分线交点,若∠BOC=110°,则∠D=( )度.
A.15° B.20° C.25° D.30°
二、填空题
9.如图,为了固定门框形状,在其上钉一根木条,其根据是三角形的 性.
10.已知 的两条边长分别为3和5,则第三边c的取值范是
11.如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF= .
12.如图,∠3=120°,则∠1-∠2= °.
13.如图,∠1,∠2,∠3,∠4是五边形 的4个外角,若 ,则
的度数为 .
三、解答题
14.已知三角形三边长分别为a、b、c,其中a、b满足(a﹣6)2+|b﹣8|=0,求这个三角形最长边c的取值范围.
15.一个多边形的内角和比外角和的 多 ,它是几边形?
16.如图,在△ABC中,∠ABC、∠ACB的平分线BE,CD相交于点F,已知∠ABC=40°,∠A=60°,求∠BFD的度数.
17.如图,在 中, 为 的高, 为 的角平分线, 交 于点G, , ,求 的大小.
18.如图,已知中,是边上的高,平分,与相交于点P,,,求和的度数.
参考答案
1.C
2.C
3.D
4.A
5.B
6.A
7.C
8.B
9.稳定
10.2<c<8
11.87°
12.60
13.130°
14.解:∵(a﹣6)2+|b﹣8|=0,∴a﹣6=0,b﹣8=0,∴a=6,b=8,b﹣a<c<a+b,这个三角形的最长边c,c>b=8,8<c<14
15.解:设这个多边形边数为 ,依题意得:
,
解得: ,
答:它是七边形
16.解:∵∠A=60°
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∵∠ABC,∠ACB的平分线BE,CD相交于点F,
∴∠FBC+∠FCB= ∠ABC+ ∠ACB= (∠ABC+∠ACB)=60°,
∵∠BFD=∠FBC+∠FCB,
∴∠BFD=60°.
17.解: 为 的高,
.
.
在 △ABE 中, .
为 的角平分线,
.
.
18.解:∵是边上的高,
∴,
在中,,
∴,
∵平分,
∴,
∵是的外角,
∴.
