北师大版九年级数学上册第6章反比例函数 单元综合练习题(含答案)
文档属性
| 名称 | 北师大版九年级数学上册第6章反比例函数 单元综合练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 462.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 17:10:18 | ||
图片预览

文档简介
北师大版九年级数学上册《第6章反比例函数》单元综合练习题
一.选择题
1.下面四个关系式中,y是x的反比例函数的是( )
A.y=3x B.y=2x2 C.y= D.y=
2.在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
A. B.
C. D.
3.如图,点P(﹣2a,a)是反比例函数y=与⊙O的一个交点,图中阴影部分的面积为10π,则该反比例函数的表达式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
4.对于反比例函数y=﹣的图象,下列说法正确的是( )
A.y随x的增大而增大 B.图象位于第一、三象限
C.图象关于直线y=﹣x对称 D.图象经过点(﹣2,﹣2)
5.已知反比例函数,当x<0时,y随x增大而减小,则a的值可能是( )
A.1 B.2 C.3 D.4
6.设函数y1=,y2=﹣(k>0).当﹣3≤x≤﹣2时,y1的最大值为a,y2的最小值为a+2,则实数a与k的值为( )
A.a=3,k=1 B.a=﹣1,k=﹣1 C.a=3,k=3 D.a=﹣1,k=3
7.如图,点A是函数图象上的任意一点,点B、C在反比例函数的图象上.若AB∥x轴,AC∥y轴,阴影部分的面积为4,则k的值是( )
A.2 B.3 C.4 D.6
8.如图,在反比例函数的图象上,有点P1,P2,P3,P4,…,Pn,…,它们的横坐标依次为1,2,3,4,…,n,…,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,…,Sn,…,则S1+S2+S3+ +S2022的结果为( )
A. B. C. D.
9.如图,在Rt△OAB中,∠OAB=90°,点A在x轴的负半轴上,点B在第二象限,反比例函数y=(x<0)的图象经过OB上一点D,与AB相交于点C,若OD=2BD,△OBC的面积为,则k的值是( )
A.﹣. B.﹣3. C. D.3
10.已知点A(x1,y2),B(x1,y2)都在反比例函数y=的图象上,且x1<x2<0,则y1,y2的大小关系是( )
A.0<y1<y2 B.y1<y2<0 C.0<y2<y1 D.y2<y1<0
11.已知反比例函数的图象上有两点A(2,y1)、B(m,y2),如果y1<y2,则实数m的取值范围是( )
A.m>2 B.m<2 C.0<m<2 D.m<0或m>2
12.已知点(﹣2,a),(2,b),(3,c)在函数y=(k为常数)的图象上,则下列判断正确的是( )
A.a<c<b B.b<a<c C.a<b<c D.c<b<a
二.填空题
13.如图,已知直线y=mx与双曲线y=的一个交点坐标为(3,4),则它们的另一个交点坐标是 .
14.如图,一次函数y=k1x+b与反比例函数y=的图象交于点A,B,其横坐标分别为1,5.则关于x的不等式k1x+b>的解集是 .
15.如图,直线y=﹣x+4与双曲线y=交于A,B两点,若△AOB的面积为4,则k的值为 .
16.如图,过原点且平行于y=3x﹣1的直线与反比例函数y=(k≠0,x>0)的图象相交于点C,过直线OC上的点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AD=2BD,那么点C的坐标为 .
三.解答题
17.已知反比例函数y=(x>0)的图象上有一点A(1,a),点C的坐标为(0,1),将线段AC绕点C按逆时针方向旋转90°,得到线段CB.
(1)求直线AB的解析式.
(2)点P是线段AB上的一点,连接CP,若CP将△ABC的面积分成2:3两部分,求点P的横坐标.
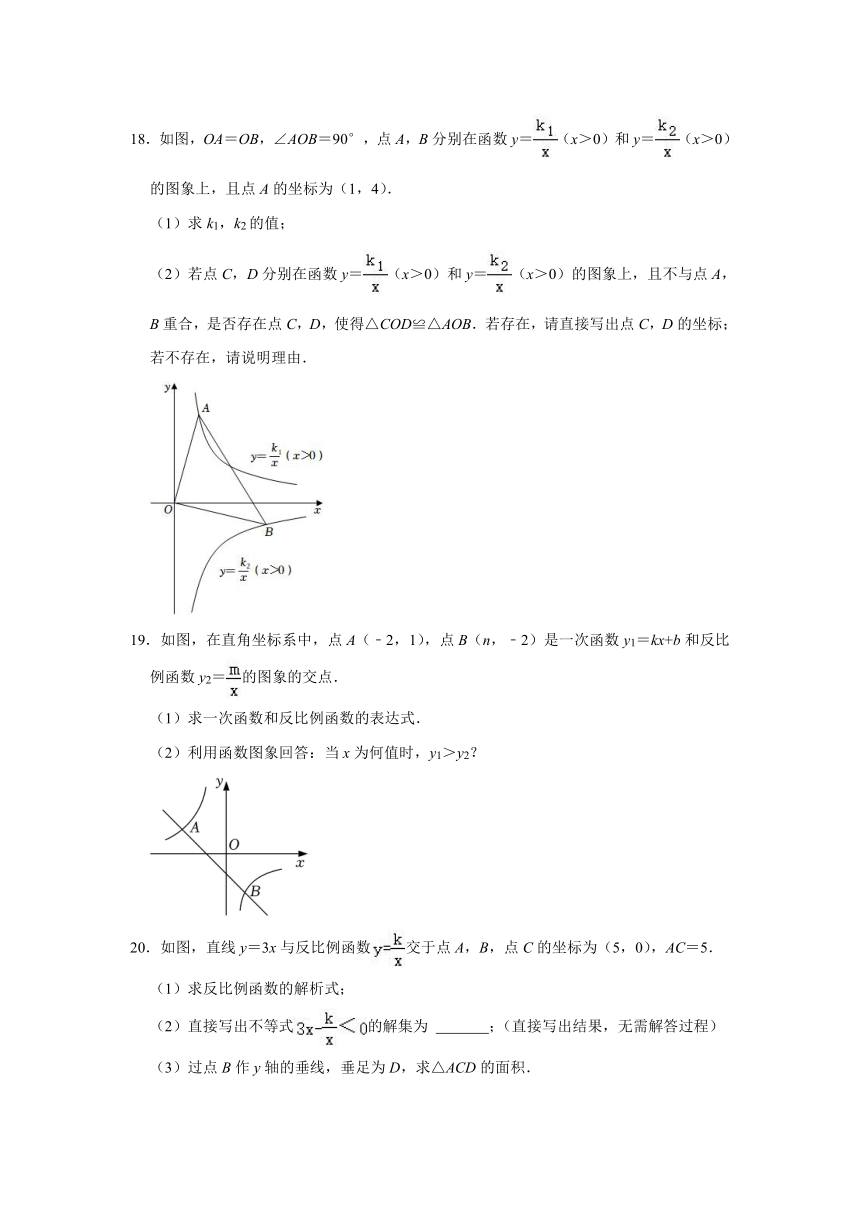
18.如图,OA=OB,∠AOB=90°,点A,B分别在函数y=(x>0)和y=(x>0)的图象上,且点A的坐标为(1,4).
(1)求k1,k2的值;
(2)若点C,D分别在函数y=(x>0)和y=(x>0)的图象上,且不与点A,B重合,是否存在点C,D,使得△COD≌△AOB.若存在,请直接写出点C,D的坐标;若不存在,请说明理由.
19.如图,在直角坐标系中,点A(﹣2,1),点B(n,﹣2)是一次函数y1=kx+b和反比例函数y2=的图象的交点.
(1)求一次函数和反比例函数的表达式.
(2)利用函数图象回答:当x为何值时,y1>y2?
20.如图,直线y=3x与反比例函数交于点A,B,点C的坐标为(5,0),AC=5.
(1)求反比例函数的解析式;
(2)直接写出不等式的解集为 ;(直接写出结果,无需解答过程)
(3)过点B作y轴的垂线,垂足为D,求△ACD的面积.
21.如图,某校科技小组计划利用已有的一堵长为6m的墙,用篱笆围一个面积为30m2的矩形科技园ABCD,设AB的长为x(m),BC的长为y(m).
(1)求y关于x的函数表达式和自变量x的取值范围.
(2)边AD和DC的长都是整数米,若围成矩形科技园ABCD三边的篱笆总长不超过20m,求出满足条件的所有围建方案.
22.A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.
(1)写出v关于t的函数表达式;
(2)若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?
(3)若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.
23.为预防传染病,某校定期对教室进行“药熏消毒”.如图,药物燃烧阶段,室内每立方米空气中的含药量y(毫克)与燃烧时间x(分)成正比例,10分钟时药物燃尽,此时教室内每立方米空气含药量为8毫克.燃尽后y与x成反比例(1)求第5分钟时教室内每立方米空气中的含药量.
(2)画出药物燃尽后y关于x的反比例函数图象;
(3)当每立方米空气中含药量低于1.6毫克时,对人体方能无毒害作用,那么从消毒开始,在哪个时段学生不能停留在教室里?
24.如图,菱形ABCD的顶点A、B分别在y轴与x轴正半轴上,C、D在第一象限,AC∥x轴,反比例函数的图象经过顶点D.
(1)若A(0,2),B(1,0).
①求反比例函数的解析式;
②证明:点C落在反比例函数的图象上;
(2)若,∠ABD=30°,求菱形ABCD的边长.
参考答案
一.选择题
1.解:A、y=3x是一次函数,故此选项不符合题意;
B、y=2x2是二次函数,故此选项不符合题意;
C、y=,符合反比例函数的形式,是反比例函数,故此选项符合题意.
D、y=不符合反比例函数的定义,故此选项不符合题意;
故选:C.
2.解:当k>0时,一次函数y=kx+1经过第一、二、三象限,反比例函数y=位于第一、三象限;
当k<0时,一次函数y=kx+1经过第一、二、四象限,反比例函数y=位于第二、四象限;
故选:D.
3.解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:πr2=10π.
解得:r=2.
∵点P(﹣2a,a)是反比例函数y=(k>0)与⊙O的一个交点.
∴﹣2a2=k且=r.
∴a2=8.
∴k=﹣2×8=﹣16,
则反比例函数的解析式是:y=﹣.
故选:D.
4.解:∵y=﹣,
∴反比例函数图象经过第二,四象限,在每个象限内y随x增大而增大,函数图象关于原点成中心对称,关于直线y=﹣x成轴对称,
故选:C.
5.解:∵反比例函数,当x<0时,y随x增大而减小,
∴2﹣a>0,
解得:a<2,
故a的值可能是1.
故选:A.
6.解:∵k>0,当﹣3≤x≤﹣2时,y1的最大值为a,
∴当x=﹣3时,a=,
∵﹣k<0,y2的最小值为a+2,
x=﹣3时,a+2=,
联立a=与a+2=,
解得a=﹣1,k=3,
故选:D.
7.解:如图,延长CA交x轴于点N,过点B作BM⊥x轴,垂足为M,
∵S阴影部分=S△CON+S矩形ABMN﹣S△BOM,而S△CON=S△BOM=|k|,
∴S阴影部分=S矩形ABMN=4,
设ON=a,
∵点A在反比例函数y=的图象上,
∴AN==BM,
又∵点B在反比例函数y=的图象上,
∴OM=,
∴MN=﹣a,
由S阴影部分=S矩形ABMN=4得,
(﹣a)×=4,
即k﹣2=4,
∴k=6,
故选:D.
8.解:当x=1时,P1的纵坐标为2,
当x=2时,P2的纵坐标1,
当x=3时,P3的纵坐标,
当x=4时,P4的纵坐标,
当x=5时,P5的纵坐标,
…
则S1=1×(2﹣1)=2﹣1;
S2=1×(1﹣)=1﹣;
S3=1×(﹣)=﹣;
S4=1×(﹣)=﹣;
…
Sn=﹣;
S1+S2+S3+…+Sn=2﹣1+1﹣+﹣+﹣+…+﹣=2﹣=.
∴S1+S2+S3+…+S2022==.
故选:D.
9.解:过点D作DE⊥AO于点E,
∵DE⊥AO,∠OAB=90°,
∴AB∥DE,
∴△OED∽△OAB,
∵OD=2BD,
∴,
∵点D和C在反比例函数图象上,
∴△AOC和△DOE的面积为,
∴,
解得:k=﹣3.
故选:B.
10.解:∵反比例函数y=中k=2>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内,y随x的增大而减小.
∵x1<x2<0,
∴A、B都在第三象限,
∴y2<y1<0.
故选:D.
11.解:∵k2>0,
∴反比例函数的图象在一、三象限,且在每个象限y随x的增大而减小,
若点A(2,y1)、B(m,y2)在同一象限,
∵y1<y2,
∴0<m<2,
若点A(2,y1)、B(m,y2)在不同象限,
则y1<y2不成立,
实数m的取值范围是0<m<2.
故选:C.
12.解:∵k2+2>0,
∴函数y=(k为常数)的图象分布在第一、三象限,在每一象限内,y随x的增大而减小,
∵﹣2<0<2<3,
∴b>c>0,a<0,
∴a<c<b.
故选:A.
二.填空题
13.解:因为直线y=mx过原点,双曲线y=的两个分支关于原点对称,
所以其交点坐标关于原点对称,一个交点坐标为(3,4),另一个交点的坐标为(﹣3,﹣4).
故答案是:(﹣3,﹣4).
14.解:如图所示:关于x的不等式k1x+b>的解集是:x<0或1<x<5.
故答案为:x<0或1<x<5.
15.解:∵直线y=﹣x+4与双曲线y=关于直线y=x对称,
∴△AOC≌△BOD,
∵直线y=﹣x+4与x轴相交于C点,与y轴交于D,
∴C(0,4),D(4,0),
∴S△COD==8,
∵△AOB的面积是4,
∴S△AOC=2,
∴×4×xA=2,
解得xA=1,
代入y=﹣x+4得,y=﹣x+4=3,
∴A(1,3),
∵双曲线y=过点A,
∴k=1×3=3,
∴k的值为3,
故答案为:3.
16.解:过原点且平行于y=3x﹣1的直线为y=3x,
∵A(1,3),
∴AB=3,OB=1,
∵AD=2BD,
∴AB=3BD,
∴BD=1,
∴D(1,1)
将D坐标代入反比例解析式得:k=1;
∴反比例函数的解析式为;y=,
由解得:或,
∵x>0,
∴C;
故答案为:.
三.解答题
17.解:(1)作AM⊥y轴于M,BN⊥y轴于N,
∵反比例函数y=(x>0)的图象上有一点A(1,a),
∴a=4,
∴A(1,4),
∵C的坐标为(0,1),将线段AC绕点C按逆时针方向旋转90°,得到线段CB,
∴△ACM≌△CBN(AAS),
∴CN=AM=1,BN=CM=4﹣1=3,
∴B(﹣3,2),
设直线AB 的解析式为y=kx+b,
∴,解得,
∴直线AB为y=x+;
(2)∵点P是线段AB上的一点,CP将△ABC的面积分成2:3两部分,
∴=或=,
∴P的横坐标为﹣或﹣.
18.解:(1)如图1,过点A作AG⊥y轴于G,过点B作BH⊥y轴于H,
∵A(1,4),
∴k1=1×4=4,AG=1,OG=4,
∵∠AOB=∠AOG+∠BOH=∠BOH+∠OBH=90°,
∴∠AOG=∠OBH,
∵OA=OB,∠AGO=∠BHO=90°,
∴△AGO≌△OHB(AAS),
∴OH=AG=1,BH=OG=4,
∴B(4,﹣1),
∴k2=4×(﹣1)=﹣4;
(2)如图2,∵△COD≌△AOB,
∴OA=OB=OC=OD,
∴B与C关于x轴对称,A与D关于x轴对称,
∴C(4,1),D(1,﹣4).
19.解:(1)∵点A(﹣2,1),点B(n,﹣2)是一次函数y1=kx+b和反比例函数y2=的图象的交点.
∴m=(﹣2)×1=﹣2,
∴反比例函数的解析式为y2=﹣,
∴﹣2n=﹣2,解得n=1,
∴B(1,﹣2),
把A(﹣2,1),B(1,﹣2)代入y1=kx+b得
,
解得 ,
∴一次函数的解析式为y1=﹣x﹣1;
(2)观察图象,当0<x<1或x<﹣2时,y1>y2.
20.解:(1)设点A坐标为(m,3m),作AE⊥x轴,则OE=m,AE=3m,
∴CE=5﹣3m,
在Rt△AEC中,AE2+CE2=AC2,
∴(3m)2+(5﹣m)2=52,
解得m=1,
∴A(1,3),
∴k=xy=3,
∴反比例函数解析式为;
(2)由反比例函数的对称性可知B(﹣1,﹣3),
∴不等式的解集为x<﹣1或0<x<1,
故答案为:x<﹣1或0<x<1;
(3)依题意点D坐标为(0,﹣3),
设直线AD的解析式为y=k1x﹣3(k1≠0),
将A点坐标代入得3=k1﹣3,解得k1=6,
∴直线AD的解析式为y=6x﹣3,
令y=0得,
∴,
∴=.
21.解:(1)依题意得:xy=30,
∴y=.
又∵墙长为6m,
∴≤6,
∴x≥5.
∴y关于x的函数表达式为y=(x≥5).
(2)∵x,y均为整数,x≥5,且y=,
∴x可以为5,6,10,15,30.
又∵2x+y≤20,即2x+≤20,
∴x可以为5,6,
∴共有2种围建方案,
方案1:AB的长为5m,BC的长为6m;
方案2:AB的长为6m,BC的长为5m.
22.解:(1)根据题意,路程为400,
设小汽车的行驶时间为t小时,行驶速度为v千米/小时,
则v关于t的函数表达式为v=;
(2)设从A地匀速行驶到B地要t小时,则≤80,
解得:t≥5,
∴他从A地匀速行驶到B地至少要5小时;
(3)∵v≤100,
≤100,
解得:t≥4,
∴某人从A地出发最少用4个小时才能到达B地,
7点至10点40分,是3小时,
∴他不能在10点40分之前到达B地.
23.解:(1)设药物燃烧阶段函数解析式为y=k1x(k1≠0),由题意得:8=10k1,
∴k1=,
∴此阶段函数解析式为y=x(0≤x≤10),
当x=5时,y=4,
故第5分钟时教室内每立方米空气中的含药量为4毫克.
(2)设药物燃烧结束后函数解析式为y=(k2≠0),由题意得:,
∴k2=80,
∴此阶段函数解析式(x≥10),
其图象如下:
(3)当y>1.6时,得,
解得x<2,
当y>1.6时,得,
∵x>0,
∴1.6x<80,
解得x<50.
即从消毒开始2分钟到50分钟之间时学生不能停留在教室里.
24.解:(1)①过点D作y轴垂线交于点F,
∴∠OFD=90°,
∵四边形ABCD为菱形,
∴BE=DE,AE=AC,BD⊥AC,
∴∠AEB=90°,
∵AC∥x轴,
∴∠OAE=90°,
∴∠OAE=∠AEB=∠AOB=90°,
∴四边形AOBE为矩形,
∴AO=BE,
∵A(0,2),B(1,0),
∴AO=BE=DE=2,AE=OB=1,
同理:四边形AEDF为矩形,
∴AF=DE=2,DF=AE=1,
∴D(1,4),
∵点D在反比例函数y=的图象上,
∴反比例函数的解析式为;
②过点C作x轴垂线交于点G,
同①的方法得,四边形AEBO、ACGO为矩形,
∴AO=CG=2,AC=2AE=2,
∴C(2,2),
∵反比例函数的解析式为,
当x=2时,y==2,
∴C落在反比例函数y=的图象上;
(2)四边形ABCD为菱形,
∴BE=DE,AE=AC,BD⊥AC,
∴∠AEB=90°,
设AE=a,
在Rt△ABE中,∠ABD=30°,
∴,AB=2a,
同(1)的方法得,,
∵k=18,
∴反比例函数的解析式为y=,
∵D在反比例函数y=的图象上,
∴,
∴a=3(由于a>0,舍去负值),
∴AB=2a=6,
即菱形ABCD的边长为6.
一.选择题
1.下面四个关系式中,y是x的反比例函数的是( )
A.y=3x B.y=2x2 C.y= D.y=
2.在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
A. B.
C. D.
3.如图,点P(﹣2a,a)是反比例函数y=与⊙O的一个交点,图中阴影部分的面积为10π,则该反比例函数的表达式为( )
A.y=﹣ B.y=﹣ C.y=﹣ D.y=﹣
4.对于反比例函数y=﹣的图象,下列说法正确的是( )
A.y随x的增大而增大 B.图象位于第一、三象限
C.图象关于直线y=﹣x对称 D.图象经过点(﹣2,﹣2)
5.已知反比例函数,当x<0时,y随x增大而减小,则a的值可能是( )
A.1 B.2 C.3 D.4
6.设函数y1=,y2=﹣(k>0).当﹣3≤x≤﹣2时,y1的最大值为a,y2的最小值为a+2,则实数a与k的值为( )
A.a=3,k=1 B.a=﹣1,k=﹣1 C.a=3,k=3 D.a=﹣1,k=3
7.如图,点A是函数图象上的任意一点,点B、C在反比例函数的图象上.若AB∥x轴,AC∥y轴,阴影部分的面积为4,则k的值是( )
A.2 B.3 C.4 D.6
8.如图,在反比例函数的图象上,有点P1,P2,P3,P4,…,Pn,…,它们的横坐标依次为1,2,3,4,…,n,…,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,…,Sn,…,则S1+S2+S3+ +S2022的结果为( )
A. B. C. D.
9.如图,在Rt△OAB中,∠OAB=90°,点A在x轴的负半轴上,点B在第二象限,反比例函数y=(x<0)的图象经过OB上一点D,与AB相交于点C,若OD=2BD,△OBC的面积为,则k的值是( )
A.﹣. B.﹣3. C. D.3
10.已知点A(x1,y2),B(x1,y2)都在反比例函数y=的图象上,且x1<x2<0,则y1,y2的大小关系是( )
A.0<y1<y2 B.y1<y2<0 C.0<y2<y1 D.y2<y1<0
11.已知反比例函数的图象上有两点A(2,y1)、B(m,y2),如果y1<y2,则实数m的取值范围是( )
A.m>2 B.m<2 C.0<m<2 D.m<0或m>2
12.已知点(﹣2,a),(2,b),(3,c)在函数y=(k为常数)的图象上,则下列判断正确的是( )
A.a<c<b B.b<a<c C.a<b<c D.c<b<a
二.填空题
13.如图,已知直线y=mx与双曲线y=的一个交点坐标为(3,4),则它们的另一个交点坐标是 .
14.如图,一次函数y=k1x+b与反比例函数y=的图象交于点A,B,其横坐标分别为1,5.则关于x的不等式k1x+b>的解集是 .
15.如图,直线y=﹣x+4与双曲线y=交于A,B两点,若△AOB的面积为4,则k的值为 .
16.如图,过原点且平行于y=3x﹣1的直线与反比例函数y=(k≠0,x>0)的图象相交于点C,过直线OC上的点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AD=2BD,那么点C的坐标为 .
三.解答题
17.已知反比例函数y=(x>0)的图象上有一点A(1,a),点C的坐标为(0,1),将线段AC绕点C按逆时针方向旋转90°,得到线段CB.
(1)求直线AB的解析式.
(2)点P是线段AB上的一点,连接CP,若CP将△ABC的面积分成2:3两部分,求点P的横坐标.
18.如图,OA=OB,∠AOB=90°,点A,B分别在函数y=(x>0)和y=(x>0)的图象上,且点A的坐标为(1,4).
(1)求k1,k2的值;
(2)若点C,D分别在函数y=(x>0)和y=(x>0)的图象上,且不与点A,B重合,是否存在点C,D,使得△COD≌△AOB.若存在,请直接写出点C,D的坐标;若不存在,请说明理由.
19.如图,在直角坐标系中,点A(﹣2,1),点B(n,﹣2)是一次函数y1=kx+b和反比例函数y2=的图象的交点.
(1)求一次函数和反比例函数的表达式.
(2)利用函数图象回答:当x为何值时,y1>y2?
20.如图,直线y=3x与反比例函数交于点A,B,点C的坐标为(5,0),AC=5.
(1)求反比例函数的解析式;
(2)直接写出不等式的解集为 ;(直接写出结果,无需解答过程)
(3)过点B作y轴的垂线,垂足为D,求△ACD的面积.
21.如图,某校科技小组计划利用已有的一堵长为6m的墙,用篱笆围一个面积为30m2的矩形科技园ABCD,设AB的长为x(m),BC的长为y(m).
(1)求y关于x的函数表达式和自变量x的取值范围.
(2)边AD和DC的长都是整数米,若围成矩形科技园ABCD三边的篱笆总长不超过20m,求出满足条件的所有围建方案.
22.A、B两地相距400千米,某人开车从A地匀速到B地,设小汽车的行驶时间为t小时,行驶速度为v千米/小时,且全程限速,速度不超过100千米/小时.
(1)写出v关于t的函数表达式;
(2)若某人开车的速度不超过每小时80千米,那么他从A地匀速行驶到B地至少要多长时间?
(3)若某人上午7点开车从A地出发,他能否在10点40分之前到达B地?请说明理由.
23.为预防传染病,某校定期对教室进行“药熏消毒”.如图,药物燃烧阶段,室内每立方米空气中的含药量y(毫克)与燃烧时间x(分)成正比例,10分钟时药物燃尽,此时教室内每立方米空气含药量为8毫克.燃尽后y与x成反比例(1)求第5分钟时教室内每立方米空气中的含药量.
(2)画出药物燃尽后y关于x的反比例函数图象;
(3)当每立方米空气中含药量低于1.6毫克时,对人体方能无毒害作用,那么从消毒开始,在哪个时段学生不能停留在教室里?
24.如图,菱形ABCD的顶点A、B分别在y轴与x轴正半轴上,C、D在第一象限,AC∥x轴,反比例函数的图象经过顶点D.
(1)若A(0,2),B(1,0).
①求反比例函数的解析式;
②证明:点C落在反比例函数的图象上;
(2)若,∠ABD=30°,求菱形ABCD的边长.
参考答案
一.选择题
1.解:A、y=3x是一次函数,故此选项不符合题意;
B、y=2x2是二次函数,故此选项不符合题意;
C、y=,符合反比例函数的形式,是反比例函数,故此选项符合题意.
D、y=不符合反比例函数的定义,故此选项不符合题意;
故选:C.
2.解:当k>0时,一次函数y=kx+1经过第一、二、三象限,反比例函数y=位于第一、三象限;
当k<0时,一次函数y=kx+1经过第一、二、四象限,反比例函数y=位于第二、四象限;
故选:D.
3.解:设圆的半径是r,根据圆的对称性以及反比例函数的对称性可得:πr2=10π.
解得:r=2.
∵点P(﹣2a,a)是反比例函数y=(k>0)与⊙O的一个交点.
∴﹣2a2=k且=r.
∴a2=8.
∴k=﹣2×8=﹣16,
则反比例函数的解析式是:y=﹣.
故选:D.
4.解:∵y=﹣,
∴反比例函数图象经过第二,四象限,在每个象限内y随x增大而增大,函数图象关于原点成中心对称,关于直线y=﹣x成轴对称,
故选:C.
5.解:∵反比例函数,当x<0时,y随x增大而减小,
∴2﹣a>0,
解得:a<2,
故a的值可能是1.
故选:A.
6.解:∵k>0,当﹣3≤x≤﹣2时,y1的最大值为a,
∴当x=﹣3时,a=,
∵﹣k<0,y2的最小值为a+2,
x=﹣3时,a+2=,
联立a=与a+2=,
解得a=﹣1,k=3,
故选:D.
7.解:如图,延长CA交x轴于点N,过点B作BM⊥x轴,垂足为M,
∵S阴影部分=S△CON+S矩形ABMN﹣S△BOM,而S△CON=S△BOM=|k|,
∴S阴影部分=S矩形ABMN=4,
设ON=a,
∵点A在反比例函数y=的图象上,
∴AN==BM,
又∵点B在反比例函数y=的图象上,
∴OM=,
∴MN=﹣a,
由S阴影部分=S矩形ABMN=4得,
(﹣a)×=4,
即k﹣2=4,
∴k=6,
故选:D.
8.解:当x=1时,P1的纵坐标为2,
当x=2时,P2的纵坐标1,
当x=3时,P3的纵坐标,
当x=4时,P4的纵坐标,
当x=5时,P5的纵坐标,
…
则S1=1×(2﹣1)=2﹣1;
S2=1×(1﹣)=1﹣;
S3=1×(﹣)=﹣;
S4=1×(﹣)=﹣;
…
Sn=﹣;
S1+S2+S3+…+Sn=2﹣1+1﹣+﹣+﹣+…+﹣=2﹣=.
∴S1+S2+S3+…+S2022==.
故选:D.
9.解:过点D作DE⊥AO于点E,
∵DE⊥AO,∠OAB=90°,
∴AB∥DE,
∴△OED∽△OAB,
∵OD=2BD,
∴,
∵点D和C在反比例函数图象上,
∴△AOC和△DOE的面积为,
∴,
解得:k=﹣3.
故选:B.
10.解:∵反比例函数y=中k=2>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内,y随x的增大而减小.
∵x1<x2<0,
∴A、B都在第三象限,
∴y2<y1<0.
故选:D.
11.解:∵k2>0,
∴反比例函数的图象在一、三象限,且在每个象限y随x的增大而减小,
若点A(2,y1)、B(m,y2)在同一象限,
∵y1<y2,
∴0<m<2,
若点A(2,y1)、B(m,y2)在不同象限,
则y1<y2不成立,
实数m的取值范围是0<m<2.
故选:C.
12.解:∵k2+2>0,
∴函数y=(k为常数)的图象分布在第一、三象限,在每一象限内,y随x的增大而减小,
∵﹣2<0<2<3,
∴b>c>0,a<0,
∴a<c<b.
故选:A.
二.填空题
13.解:因为直线y=mx过原点,双曲线y=的两个分支关于原点对称,
所以其交点坐标关于原点对称,一个交点坐标为(3,4),另一个交点的坐标为(﹣3,﹣4).
故答案是:(﹣3,﹣4).
14.解:如图所示:关于x的不等式k1x+b>的解集是:x<0或1<x<5.
故答案为:x<0或1<x<5.
15.解:∵直线y=﹣x+4与双曲线y=关于直线y=x对称,
∴△AOC≌△BOD,
∵直线y=﹣x+4与x轴相交于C点,与y轴交于D,
∴C(0,4),D(4,0),
∴S△COD==8,
∵△AOB的面积是4,
∴S△AOC=2,
∴×4×xA=2,
解得xA=1,
代入y=﹣x+4得,y=﹣x+4=3,
∴A(1,3),
∵双曲线y=过点A,
∴k=1×3=3,
∴k的值为3,
故答案为:3.
16.解:过原点且平行于y=3x﹣1的直线为y=3x,
∵A(1,3),
∴AB=3,OB=1,
∵AD=2BD,
∴AB=3BD,
∴BD=1,
∴D(1,1)
将D坐标代入反比例解析式得:k=1;
∴反比例函数的解析式为;y=,
由解得:或,
∵x>0,
∴C;
故答案为:.
三.解答题
17.解:(1)作AM⊥y轴于M,BN⊥y轴于N,
∵反比例函数y=(x>0)的图象上有一点A(1,a),
∴a=4,
∴A(1,4),
∵C的坐标为(0,1),将线段AC绕点C按逆时针方向旋转90°,得到线段CB,
∴△ACM≌△CBN(AAS),
∴CN=AM=1,BN=CM=4﹣1=3,
∴B(﹣3,2),
设直线AB 的解析式为y=kx+b,
∴,解得,
∴直线AB为y=x+;
(2)∵点P是线段AB上的一点,CP将△ABC的面积分成2:3两部分,
∴=或=,
∴P的横坐标为﹣或﹣.
18.解:(1)如图1,过点A作AG⊥y轴于G,过点B作BH⊥y轴于H,
∵A(1,4),
∴k1=1×4=4,AG=1,OG=4,
∵∠AOB=∠AOG+∠BOH=∠BOH+∠OBH=90°,
∴∠AOG=∠OBH,
∵OA=OB,∠AGO=∠BHO=90°,
∴△AGO≌△OHB(AAS),
∴OH=AG=1,BH=OG=4,
∴B(4,﹣1),
∴k2=4×(﹣1)=﹣4;
(2)如图2,∵△COD≌△AOB,
∴OA=OB=OC=OD,
∴B与C关于x轴对称,A与D关于x轴对称,
∴C(4,1),D(1,﹣4).
19.解:(1)∵点A(﹣2,1),点B(n,﹣2)是一次函数y1=kx+b和反比例函数y2=的图象的交点.
∴m=(﹣2)×1=﹣2,
∴反比例函数的解析式为y2=﹣,
∴﹣2n=﹣2,解得n=1,
∴B(1,﹣2),
把A(﹣2,1),B(1,﹣2)代入y1=kx+b得
,
解得 ,
∴一次函数的解析式为y1=﹣x﹣1;
(2)观察图象,当0<x<1或x<﹣2时,y1>y2.
20.解:(1)设点A坐标为(m,3m),作AE⊥x轴,则OE=m,AE=3m,
∴CE=5﹣3m,
在Rt△AEC中,AE2+CE2=AC2,
∴(3m)2+(5﹣m)2=52,
解得m=1,
∴A(1,3),
∴k=xy=3,
∴反比例函数解析式为;
(2)由反比例函数的对称性可知B(﹣1,﹣3),
∴不等式的解集为x<﹣1或0<x<1,
故答案为:x<﹣1或0<x<1;
(3)依题意点D坐标为(0,﹣3),
设直线AD的解析式为y=k1x﹣3(k1≠0),
将A点坐标代入得3=k1﹣3,解得k1=6,
∴直线AD的解析式为y=6x﹣3,
令y=0得,
∴,
∴=.
21.解:(1)依题意得:xy=30,
∴y=.
又∵墙长为6m,
∴≤6,
∴x≥5.
∴y关于x的函数表达式为y=(x≥5).
(2)∵x,y均为整数,x≥5,且y=,
∴x可以为5,6,10,15,30.
又∵2x+y≤20,即2x+≤20,
∴x可以为5,6,
∴共有2种围建方案,
方案1:AB的长为5m,BC的长为6m;
方案2:AB的长为6m,BC的长为5m.
22.解:(1)根据题意,路程为400,
设小汽车的行驶时间为t小时,行驶速度为v千米/小时,
则v关于t的函数表达式为v=;
(2)设从A地匀速行驶到B地要t小时,则≤80,
解得:t≥5,
∴他从A地匀速行驶到B地至少要5小时;
(3)∵v≤100,
≤100,
解得:t≥4,
∴某人从A地出发最少用4个小时才能到达B地,
7点至10点40分,是3小时,
∴他不能在10点40分之前到达B地.
23.解:(1)设药物燃烧阶段函数解析式为y=k1x(k1≠0),由题意得:8=10k1,
∴k1=,
∴此阶段函数解析式为y=x(0≤x≤10),
当x=5时,y=4,
故第5分钟时教室内每立方米空气中的含药量为4毫克.
(2)设药物燃烧结束后函数解析式为y=(k2≠0),由题意得:,
∴k2=80,
∴此阶段函数解析式(x≥10),
其图象如下:
(3)当y>1.6时,得,
解得x<2,
当y>1.6时,得,
∵x>0,
∴1.6x<80,
解得x<50.
即从消毒开始2分钟到50分钟之间时学生不能停留在教室里.
24.解:(1)①过点D作y轴垂线交于点F,
∴∠OFD=90°,
∵四边形ABCD为菱形,
∴BE=DE,AE=AC,BD⊥AC,
∴∠AEB=90°,
∵AC∥x轴,
∴∠OAE=90°,
∴∠OAE=∠AEB=∠AOB=90°,
∴四边形AOBE为矩形,
∴AO=BE,
∵A(0,2),B(1,0),
∴AO=BE=DE=2,AE=OB=1,
同理:四边形AEDF为矩形,
∴AF=DE=2,DF=AE=1,
∴D(1,4),
∵点D在反比例函数y=的图象上,
∴反比例函数的解析式为;
②过点C作x轴垂线交于点G,
同①的方法得,四边形AEBO、ACGO为矩形,
∴AO=CG=2,AC=2AE=2,
∴C(2,2),
∵反比例函数的解析式为,
当x=2时,y==2,
∴C落在反比例函数y=的图象上;
(2)四边形ABCD为菱形,
∴BE=DE,AE=AC,BD⊥AC,
∴∠AEB=90°,
设AE=a,
在Rt△ABE中,∠ABD=30°,
∴,AB=2a,
同(1)的方法得,,
∵k=18,
∴反比例函数的解析式为y=,
∵D在反比例函数y=的图象上,
∴,
∴a=3(由于a>0,舍去负值),
∴AB=2a=6,
即菱形ABCD的边长为6.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
