1.2.1(2)充要条件课件第2课时-2023-2024学年高一上学期数学北师大版(2019)必修第一册(共26张PPT)
文档属性
| 名称 | 1.2.1(2)充要条件课件第2课时-2023-2024学年高一上学期数学北师大版(2019)必修第一册(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 08:14:35 | ||
图片预览








文档简介
§2 常用逻辑用语
1.2.1 充要条件
2.充分条件,必要条件的判断步骤
①分清命题的条件和结论,转化为命题的基本结构:“若p,则q”形式;
②判断命题“若p,则q”的真假;
③根据定义得出结论,在“若p,则q”是真命题的前提下,
称q是p的必要条件,也称p是q的充分条件
④除了用判断命题的真假判断充分条件之外,还可以用集合关系来判断必要条件
【1】 p?q
?
【2】 p是q的充分条件
【3】 q的充分条件是p
【4】 q是p的必要条件
【5】 p的必要条件是q
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 命题真假
“若p,则q”是真命题
“若p,则q”是假命题
推出关系
p__q
p___q
条件关系
p是q的____条件
q是p的____条件
p不是q的____条件
q不是p的____条件
1.必要条件与充分条件的定义
?
?
3. 从集合角度判定逻辑关系: 对于命题“若p,则q”,
设集合A={x|x满足条件p},B={x|x满足条件q},
若A?B,则p?q, p是q的充分条件,q是p的必要条件
若A?B,则p是q的充分条件,
q是p的必要条件
若B?A,则p是q的必要条件,
则q是p的充分条件
若A=B,则p,q互为充要条件
若A B,且B A,
则p是q的既不充分又不必要条件
从集合的角度可知,
小范围? 大范围 , 所以说
“小范围”是“大范围”的充分条件, “大范围”的充分条件是“小范围”
也可以说
“大范围”是“小范围”的必要条件, “小范围”的必要条件是“大范围”
p?q,且q?p
?
p?q,且q?p
?
p?q,且q?p
?
p?q,且q?p
?
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分也不必要条件
3.充分条件 必要条件分类
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 结论
p是q的充分不必要条件
p是q的必要不充分条件
p与q互为充要条件
p是q的既不充分也不必要条件
p,q的关系
?????????,且?????????
?????????,且?????????
?????????
?????????,且?????????
集合
?????????
?????????
????=????
A B且B A
4.充分条件 必要条件传递性
例:若p是r的充分不必要条件,r是q的必要条件,
r是s的充分条件,q是s的必要条件,则q是p的什么条件?
传递性: ??“?”和“?”都具有传递性,即
①如果p?q,q?s,则p?s; ②如果p?q,q?s,则p?s;
若问题中出现若干个条件和结论,应先根据条件画出相应的“推式图”,
再根据图中推式的传递性进行判断
?
????
?
????
?
????
?
????
?
?
?
?
?
?
?
?
?
?
?
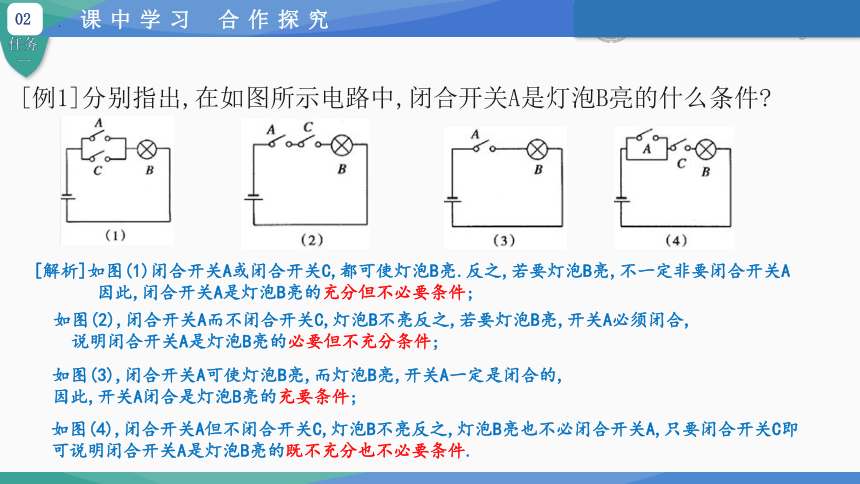
[例1]分别指出,在如图所示电路中,闭合开关A是灯泡B亮的什么条件?
[解析]如图(1)闭合开关A或闭合开关C,都可使灯泡B亮.反之,若要灯泡B亮,不一定非要闭合开关A
因此,闭合开关A是灯泡B亮的充分但不必要条件;
如图(2),闭合开关A而不闭合开关C,灯泡B不亮反之,若要灯泡B亮,开关A必须闭合,
说明闭合开关A是灯泡B亮的必要但不充分条件;
如图(3),闭合开关A可使灯泡B亮,而灯泡B亮,开关A一定是闭合的,
因此,开关A闭合是灯泡B亮的充要条件;
如图(4),闭合开关A但不闭合开关C,灯泡B不亮反之,灯泡B亮也不必闭合开关A,只要闭合开关C即 可说明闭合开关A是灯泡B亮的既不充分也不必要条件.
【课堂评价1】.用“充分不必要”“必要不充分”充要”“既不充分也不必要”填空
(1) “x=1”是“ |x|=1”的 条件.
(2)“×≠1是“|x|≠1”的 条件
(3)“x ≠ 1是“x2+2x?3 ≠ 0”的 条件
(4)“个位数字是5的自然数”是“这个自然数能被5整除”的 条件
(5)“x>1”是“ x2>1”的 条件.
(6)“x>1”是“ x3>1”的 条件.
(7)“x>1”是“ 1????<1”的 条件.
(8)“x<1”是“ 1????>1”的 条件.
?
充分不必要
必要不充分
必要不充分
充分不必要
充分不必要
充要
充分不必要
既不充分也不必要
课中学习 合作探究
02
【课堂评价】 :p是r的充分不必要条件,r是q的必要条件,
r是s的充分条件,q是s的必要条件,则下列命题,
正确的序号有 .
① p是q的充要条件
② p是q的充分条件而不是必要条件;
③ r是q的必要而不是充分条件;
④p是s的必要条件而不是充分条件
⑤r是s的充分条件而不是必要条件
⑥r是p的必要条件而不是充分条件
????
?
????
?
????
?
????
?
?
?
?
?
?
?
?
?
?
?
② ⑥
问题1:请用充分条件或必要条件的语言表述勾股定理及其逆定理
勾股定理 如果一个三角形为直角三角形
那么它的两直角边的平方和等于斜边的平方
勾股定理的逆定理 如果一个三角形的一边的平方等于其他两边的平方和
那么这条边所对的角是直角
在勾股定理中,
“两直角边的平方和等于斜边的平方”是“三角形为直角三角形”的必要条件;
“三角形为直角三角形”是“两直角边的平方和等于斜边的平方”的充分条件
勾股定理刻画了直角形的性质定理
在勾股定理的逆定理中,
“三角形的一个角是直角”是“三角形的直角所对的边的平方等于其他两边的平方和”的必要条件;
“三角形的一边的平方等于其他两边的平方和”是“这条边所对的角是直角”的充分条件
勾股定理的逆定理刻画了直角形的判定定理定理
问题2:请同学们对直角三角形下一个定义,思考:数学定义体现了怎样的逻辑关系
(1)有一个角是直角的三角形称为直角三角形
(2)三角形的一边的平方等于其他两边的平方和的三角形称为直角三角形
(3)三角形一边上的中线等于该边长的一半的三角形称为直角三角形
……
问题3:请问下列两种说法一样吗?
(1) 有一个角是直角的三角形称为直角三角形
(2) 有一个角是直角的三角形是直角三角形
不一样,(1)是直角三角形的定义;(2)是直角三角形的判定定理
数学定义给出了数学对象成立的充要条件,它是从充分性和必要性两个方面刻画数学对象的,
它既是这个数学对象的判定定理又是性质定理.
问题4:数学定义与判定定理、性质定理的区别和联系是什么
【注意】p是q的充要条件也可以说成:
①p和q是等价的
②p成立当且仅当q成立
③q成立当且仅当p成立
一般地,如果p?q,且q?p那么称p是q的充分且必要条件,
简称p是q的充要条件,记作?????????,
p是q的充要条件也常常说成
“p成立当且仅当q成立”,或“p与q等价”
当p是q的充要条件时,q也是p的充要条件
?
我们常用“当且仅当”来表达充要条件.
p是q的充要条件也可以说成:q成立当且仅当p成立.
例3.设n∈N+,一元二次方程x2-4x+n=0有整数根的充要条件是n= .
3或4
解析 由Δ=16-4n≥0,得n≤4,又n∈N+,则n=1,2,3,4.
当n=1,2时,方程没有整数根;
当n=3时,方程有整数根1,3,
当n=4时,方程有整数根2.
综上可知,n=3或4.
析:先探求一元二次方程x2-4x+n=0有根的条件,即先寻找必要条件,然后在必要条件的范围内,通过检验,寻找使之成立的所有的充分条件,即从充分性和必要性两方面找出充要条件
解:方程????^????+(?????????????)????+????^????=????有两个正实数根等价于?=(2?????1)^2?4????^2≥0????1+????2=?(2?????1)>0????1????2=????^2>0解得
????≤????????且????≠0以上每一步都是等价的,因此他的充要条件????≤????????且????≠0
?
【课堂评价4】 已知方程x2+(2k-1)x+k2=0,求使方程有两个正实数根的充要条件.
【课堂评价】
例4 (1)已知a>0,设p:-a≤x≤3a, q:- 2 ≤ x ≤ 6,
若p是q的充分不必要条件,则实数a的取值范围是( )
(2)已知a>0,设p:-a≤x≤3a, q:- 3 ≤ x ≤ 6,
若p是q的充分不必要条件,则实数a的取值范围是( )
(3)已知a>0,设p:-a≤x≤3a, q:- 2 ≤ x ≤ 6,
若p是q的必要不充分条件,则实数a的取值范围是( )
A.(2,+∞) B. [2 ,+∞) C.(0,2) D.(0,2]
?
(2) ?????,3???? ? ?3,6
?
(3)?2,6??????,3????
?
C
D
A
析(1) ?????,3???? ? ?2,6
?
【课堂评价1】 关于x的方程ax2+2x+1=0至少有一个负实根的充要条件是( )
A.0答案 C
解析(排除法)当a=1时,方程有负实根x=-1;当a=0时,方程有负实根x=?12,排除A、B、D,
?
解法2(讨论法) ①当a=0时,x=?12,符合题意.
②当a≠0时,显然方程没有零根.
若方程有两个异号实根,则a<0.
若方程有两个负的实根,则必须满足?=4?4????≥0?2????<01????>0解得0综上,若方程至少有一个负的实根,则a≤1.
反之,若a≤1,则方程至少有一个负的实根,
所以关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件是a≤1.
?
1.填空:
(1)“一元二次方程????2+????????+1=0有实数根”的充要条件是 ;
(2)“一元二次方程???????????????????1=0有一个正实数根和一个负实数根”的
一个充分条件但不是必要条件的是 ;
(3)“一元二次方程????2+????????+1=0有两个不相等的正实数根”的充要条件是 ;
?
1.(1)?∞,?2∪2,+∞;(2)????=?12(答案不唯一);(3)?∞,?2
?
P22习B组1巩固练习
写出今天学习内容的思维导图
01
完成本节对应的巩固训练(课代表收齐后上交)
完成课本第 页习题(明天课堂检查)
02
03
学习本节课后,你会 吗?
01
在课堂上你积极吗?
在这节课上你的学习目标完成了吗?
你对本堂课重难点掌握了吗?
02
03
04
05
在本节课上你掌握了哪些知识点和题型?
P15练习1、2巩固复习
练习1. 用必要条件、充分条件的语言表述下面的性质:
(1)若A=Φ,则A?B;
(2)正方形的对角线互相垂直且相等;
(3)两条直线被第三条直线所截,如果两条直线平行,那么同位角相等
2.判断下列各组中,是否有?????????或?????????成立,并用充分条件必要条件的语言表述:
(1) ????:????2=????2,????:????=????;
(2) ????:????=????,????≠0,????:????????=????????;
(3) p:能被5整除的整数, q:整数的个位数字为5;
(4) p:两个三角形全等,q:两个三角形的面积相等
?
析(1)A=Φ是A?B的充分不必要条件; A?B是A=Φ的必要不充分条件;
?
(2)一个四边形是正方形是它的对角线互相垂直且相等的充分不必要条件;
四边形的对角线互相垂直且相等是四边形是正方形的必要不充分条件;
(3)两条直线被第三条直线所截, 两条直线平行是同位角相等的充要条件
(1)p?????,??????????, p是????的必要不充分条件
?
(2)?????????,??????????, 即????????? ,p是????的充要条件
?
(3)p?????,??????????, p是????的必要不充分条件
?
(4)????????? ?????????, p是????的充分不必要条件
?
例2用充分条件必要条件的语言表述下面的命题
(1)若a=-b,则|a|=|b|
(2)若点C是线段AB的中点则AC=BC;
(3)当ac<0时,一元二次方程ax2+bx+c=0有两个不相等的实数根解
(1)“a=-b”是“|a|=b|”的充分不必要条件;
(2)“点C是线段AB的中点”是“AC=BC“的充分不必要条件;
(3)“ac<0”是“一元二次方程ax2+bx+c=0有两个不相等的实数根”的充分不必要条件
P16例2巩固复习
1.下列各题中试判断p是q的什么条件。
(1)????:????????=????????????????≠0,????:????2=????????;
(2)对于反比例函数????=????????,????>0,????>0,?q:y值随x值的增大而减小;
(3)p:函数的图象关于y轴对称,q:函数????=????2。
2.用充分条件或必要条件的语言表述下面的定理
(1)在一个平面内,垂直于同一条直线的两条直线平行;
(2) 若a>b, c<0 ,则 ac(3)一组对边平行且相等的四边形是平行四边形;
(4)如果????1,????2是一元二次方程????????2+????????+????=0(????≠0)的两个实数根,那么????1+????2=?????????。
?
(1)????????? ?????????, p是????的充分不必要条件
?
(2)?????????,??????????, 即????????? ,p是????的充要条件
?
(3)p?????,??????????, p是????的必要不充分条件
?
(1)在一个平面内,
“两条直线垂直于同一条直线”
是“这两条直线平行"的充要条件;
(2)“a>b, c<0”是“ac(3)“四边形的一组对边平行且相等”是“四边形是平行四边形”的充要条件
(4)已知方程????????2+????????+????=0(????≠0),则“????1,????2是方程的两个实数根”是“????1+????2=?????????”的充分不必要条件
?
P16练习1、2巩固复习
例3在下列各题中,试判断是p是q的什么条件
(1)p:A?B, q:A∩B=A;
(2)p:a=b,q:|a|=|bl;
(3)p:四边形的对角线相等,q:四边形是平行四边形
?
(1)?????????,??????????, 即????????? ,p是????的充要条件
?
(2)????????? ?????????, p是????的充分不必要条件
?
(3)p?????,??????????, p是????的即不充分又不必要条件
?
P17例3巩固复习
1.用“充分条件”“必要条件”或“充要条件”填空:
(1)“????∈N”是“????∈Q”的 。
(2)“????=2”是“????2?3????+2=0”的 。
(3) “????>2”是“????>3”的 。
(4)“????????>0”是“????????>0”的 。
2.下列各题中,试判断p是q的什么条件。
(1)????:1????<1,????:????>1;
(2)?????:四边形的对角线相等,????:四边形是矩形;
(3)?????:一元二次函数????=????????2+????(????≠0),?????:一元二次函数的图象关于y轴对称。
3.已知集合????=????|????=2????,????∈Z,????=????|????=4????+2,????∈Z,设????:????∈????,????:????∈????,试判断p是q的什么条件,q是p的什么条件。
?
(3)????????? ?????????, p是????的充分不必要条件
?
(1)p?????,??????????, p是????的必要不充分条件
?
(2) 充分不必要条件;
(1) 的充分不必要条件
必要不充分条件
充要条件
(2)p?????,??????????, p是????的必要不充分条件
?
3. p?????,??????????, p是????的必要不充分条件,????是p的充分不必要条件
?
P18练习1、2、3巩固复习
1.请在“充分条件”“必要条件”“充要条件”“既不是充分条件也不是必要条件"中选择一个最恰当的,填空:
(1)当?????????时,“????∈????”是“????∈????”的 ;
(2)“????是偶数,?????是偶数”是“???????? 是偶数”的 ;
(3)“?????????”是“????∪????=????” 的 ;
(4)“????????>0”是“????>0,且????>0”的 ;
(5“整数????能被3整除"是“整数????能被6整除”的 ;
(6)“????-2=0”是“(???? +2)(????? -2)=0”的 ;
(7)“????=?”是“????∩????=?”的 ;
(8)“????=????”是“????2+????2≥2????????”的 。
2.判断下列说法是否正确:
(1) “????∈N”是“????∈Z”的充分条件;
(2)“????b=0”是“a2+b2=0”的充要条件:
(3)“两个三角形全等”是“两个三角形相似”的充分条件;
(4)“两个三角形中有两边及其中一边的对角分别相等”是“两个三角形全等”的充要条件。
?
充分不必要条件;
充分不必要条件
必要不充分条件
充要条件
必要不充分条件
充分不必要条件;
充分不必要条件;
充分不必要条件;
正确
正确
错误,必要条件
错误,必要条件
P22习A组1、2巩固复习
例1 .设集合A={1,????2,-2} ,集合B={2,4},则“????=2”是“????∩????=4”的( )条件.
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
?
【解】若a=2,则A={1,4,-2},A∩B=4,满足充分条件要求;
?
若A∩B=4,则????2=4,解得a=2或a=?2?,不满足必要条件要求;
?
所以“????=2”是“????∩????=4”的充分不必要条件,选A
?
A
已知集合M={x|x<-3或x>5},P={x|(x-a)·(x-8)≤0} ,
则M∩P={x|5-3
5
1.2.1 充要条件
2.充分条件,必要条件的判断步骤
①分清命题的条件和结论,转化为命题的基本结构:“若p,则q”形式;
②判断命题“若p,则q”的真假;
③根据定义得出结论,在“若p,则q”是真命题的前提下,
称q是p的必要条件,也称p是q的充分条件
④除了用判断命题的真假判断充分条件之外,还可以用集合关系来判断必要条件
【1】 p?q
?
【2】 p是q的充分条件
【3】 q的充分条件是p
【4】 q是p的必要条件
【5】 p的必要条件是q
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 命题真假
“若p,则q”是真命题
“若p,则q”是假命题
推出关系
p__q
p___q
条件关系
p是q的____条件
q是p的____条件
p不是q的____条件
q不是p的____条件
1.必要条件与充分条件的定义
?
?
3. 从集合角度判定逻辑关系: 对于命题“若p,则q”,
设集合A={x|x满足条件p},B={x|x满足条件q},
若A?B,则p?q, p是q的充分条件,q是p的必要条件
若A?B,则p是q的充分条件,
q是p的必要条件
若B?A,则p是q的必要条件,
则q是p的充分条件
若A=B,则p,q互为充要条件
若A B,且B A,
则p是q的既不充分又不必要条件
从集合的角度可知,
小范围? 大范围 , 所以说
“小范围”是“大范围”的充分条件, “大范围”的充分条件是“小范围”
也可以说
“大范围”是“小范围”的必要条件, “小范围”的必要条件是“大范围”
p?q,且q?p
?
p?q,且q?p
?
p?q,且q?p
?
p?q,且q?p
?
p是q的充分不必要条件
p是q的必要不充分条件
p是q的充要条件
p是q的既不充分也不必要条件
3.充分条件 必要条件分类
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 结论
p是q的充分不必要条件
p是q的必要不充分条件
p与q互为充要条件
p是q的既不充分也不必要条件
p,q的关系
?????????,且?????????
?????????,且?????????
?????????
?????????,且?????????
集合
?????????
?????????
????=????
A B且B A
4.充分条件 必要条件传递性
例:若p是r的充分不必要条件,r是q的必要条件,
r是s的充分条件,q是s的必要条件,则q是p的什么条件?
传递性: ??“?”和“?”都具有传递性,即
①如果p?q,q?s,则p?s; ②如果p?q,q?s,则p?s;
若问题中出现若干个条件和结论,应先根据条件画出相应的“推式图”,
再根据图中推式的传递性进行判断
?
????
?
????
?
????
?
????
?
?
?
?
?
?
?
?
?
?
?
[例1]分别指出,在如图所示电路中,闭合开关A是灯泡B亮的什么条件?
[解析]如图(1)闭合开关A或闭合开关C,都可使灯泡B亮.反之,若要灯泡B亮,不一定非要闭合开关A
因此,闭合开关A是灯泡B亮的充分但不必要条件;
如图(2),闭合开关A而不闭合开关C,灯泡B不亮反之,若要灯泡B亮,开关A必须闭合,
说明闭合开关A是灯泡B亮的必要但不充分条件;
如图(3),闭合开关A可使灯泡B亮,而灯泡B亮,开关A一定是闭合的,
因此,开关A闭合是灯泡B亮的充要条件;
如图(4),闭合开关A但不闭合开关C,灯泡B不亮反之,灯泡B亮也不必闭合开关A,只要闭合开关C即 可说明闭合开关A是灯泡B亮的既不充分也不必要条件.
【课堂评价1】.用“充分不必要”“必要不充分”充要”“既不充分也不必要”填空
(1) “x=1”是“ |x|=1”的 条件.
(2)“×≠1是“|x|≠1”的 条件
(3)“x ≠ 1是“x2+2x?3 ≠ 0”的 条件
(4)“个位数字是5的自然数”是“这个自然数能被5整除”的 条件
(5)“x>1”是“ x2>1”的 条件.
(6)“x>1”是“ x3>1”的 条件.
(7)“x>1”是“ 1????<1”的 条件.
(8)“x<1”是“ 1????>1”的 条件.
?
充分不必要
必要不充分
必要不充分
充分不必要
充分不必要
充要
充分不必要
既不充分也不必要
课中学习 合作探究
02
【课堂评价】 :p是r的充分不必要条件,r是q的必要条件,
r是s的充分条件,q是s的必要条件,则下列命题,
正确的序号有 .
① p是q的充要条件
② p是q的充分条件而不是必要条件;
③ r是q的必要而不是充分条件;
④p是s的必要条件而不是充分条件
⑤r是s的充分条件而不是必要条件
⑥r是p的必要条件而不是充分条件
????
?
????
?
????
?
????
?
?
?
?
?
?
?
?
?
?
?
② ⑥
问题1:请用充分条件或必要条件的语言表述勾股定理及其逆定理
勾股定理 如果一个三角形为直角三角形
那么它的两直角边的平方和等于斜边的平方
勾股定理的逆定理 如果一个三角形的一边的平方等于其他两边的平方和
那么这条边所对的角是直角
在勾股定理中,
“两直角边的平方和等于斜边的平方”是“三角形为直角三角形”的必要条件;
“三角形为直角三角形”是“两直角边的平方和等于斜边的平方”的充分条件
勾股定理刻画了直角形的性质定理
在勾股定理的逆定理中,
“三角形的一个角是直角”是“三角形的直角所对的边的平方等于其他两边的平方和”的必要条件;
“三角形的一边的平方等于其他两边的平方和”是“这条边所对的角是直角”的充分条件
勾股定理的逆定理刻画了直角形的判定定理定理
问题2:请同学们对直角三角形下一个定义,思考:数学定义体现了怎样的逻辑关系
(1)有一个角是直角的三角形称为直角三角形
(2)三角形的一边的平方等于其他两边的平方和的三角形称为直角三角形
(3)三角形一边上的中线等于该边长的一半的三角形称为直角三角形
……
问题3:请问下列两种说法一样吗?
(1) 有一个角是直角的三角形称为直角三角形
(2) 有一个角是直角的三角形是直角三角形
不一样,(1)是直角三角形的定义;(2)是直角三角形的判定定理
数学定义给出了数学对象成立的充要条件,它是从充分性和必要性两个方面刻画数学对象的,
它既是这个数学对象的判定定理又是性质定理.
问题4:数学定义与判定定理、性质定理的区别和联系是什么
【注意】p是q的充要条件也可以说成:
①p和q是等价的
②p成立当且仅当q成立
③q成立当且仅当p成立
一般地,如果p?q,且q?p那么称p是q的充分且必要条件,
简称p是q的充要条件,记作?????????,
p是q的充要条件也常常说成
“p成立当且仅当q成立”,或“p与q等价”
当p是q的充要条件时,q也是p的充要条件
?
我们常用“当且仅当”来表达充要条件.
p是q的充要条件也可以说成:q成立当且仅当p成立.
例3.设n∈N+,一元二次方程x2-4x+n=0有整数根的充要条件是n= .
3或4
解析 由Δ=16-4n≥0,得n≤4,又n∈N+,则n=1,2,3,4.
当n=1,2时,方程没有整数根;
当n=3时,方程有整数根1,3,
当n=4时,方程有整数根2.
综上可知,n=3或4.
析:先探求一元二次方程x2-4x+n=0有根的条件,即先寻找必要条件,然后在必要条件的范围内,通过检验,寻找使之成立的所有的充分条件,即从充分性和必要性两方面找出充要条件
解:方程????^????+(?????????????)????+????^????=????有两个正实数根等价于?=(2?????1)^2?4????^2≥0????1+????2=?(2?????1)>0????1????2=????^2>0解得
????≤????????且????≠0以上每一步都是等价的,因此他的充要条件????≤????????且????≠0
?
【课堂评价4】 已知方程x2+(2k-1)x+k2=0,求使方程有两个正实数根的充要条件.
【课堂评价】
例4 (1)已知a>0,设p:-a≤x≤3a, q:- 2 ≤ x ≤ 6,
若p是q的充分不必要条件,则实数a的取值范围是( )
(2)已知a>0,设p:-a≤x≤3a, q:- 3 ≤ x ≤ 6,
若p是q的充分不必要条件,则实数a的取值范围是( )
(3)已知a>0,设p:-a≤x≤3a, q:- 2 ≤ x ≤ 6,
若p是q的必要不充分条件,则实数a的取值范围是( )
A.(2,+∞) B. [2 ,+∞) C.(0,2) D.(0,2]
?
(2) ?????,3???? ? ?3,6
?
(3)?2,6??????,3????
?
C
D
A
析(1) ?????,3???? ? ?2,6
?
【课堂评价1】 关于x的方程ax2+2x+1=0至少有一个负实根的充要条件是( )
A.0
解析(排除法)当a=1时,方程有负实根x=-1;当a=0时,方程有负实根x=?12,排除A、B、D,
?
解法2(讨论法) ①当a=0时,x=?12,符合题意.
②当a≠0时,显然方程没有零根.
若方程有两个异号实根,则a<0.
若方程有两个负的实根,则必须满足?=4?4????≥0?2????<01????>0解得0
反之,若a≤1,则方程至少有一个负的实根,
所以关于x的方程ax2+2x+1=0至少有一个负的实根的充要条件是a≤1.
?
1.填空:
(1)“一元二次方程????2+????????+1=0有实数根”的充要条件是 ;
(2)“一元二次方程???????????????????1=0有一个正实数根和一个负实数根”的
一个充分条件但不是必要条件的是 ;
(3)“一元二次方程????2+????????+1=0有两个不相等的正实数根”的充要条件是 ;
?
1.(1)?∞,?2∪2,+∞;(2)????=?12(答案不唯一);(3)?∞,?2
?
P22习B组1巩固练习
写出今天学习内容的思维导图
01
完成本节对应的巩固训练(课代表收齐后上交)
完成课本第 页习题(明天课堂检查)
02
03
学习本节课后,你会 吗?
01
在课堂上你积极吗?
在这节课上你的学习目标完成了吗?
你对本堂课重难点掌握了吗?
02
03
04
05
在本节课上你掌握了哪些知识点和题型?
P15练习1、2巩固复习
练习1. 用必要条件、充分条件的语言表述下面的性质:
(1)若A=Φ,则A?B;
(2)正方形的对角线互相垂直且相等;
(3)两条直线被第三条直线所截,如果两条直线平行,那么同位角相等
2.判断下列各组中,是否有?????????或?????????成立,并用充分条件必要条件的语言表述:
(1) ????:????2=????2,????:????=????;
(2) ????:????=????,????≠0,????:????????=????????;
(3) p:能被5整除的整数, q:整数的个位数字为5;
(4) p:两个三角形全等,q:两个三角形的面积相等
?
析(1)A=Φ是A?B的充分不必要条件; A?B是A=Φ的必要不充分条件;
?
(2)一个四边形是正方形是它的对角线互相垂直且相等的充分不必要条件;
四边形的对角线互相垂直且相等是四边形是正方形的必要不充分条件;
(3)两条直线被第三条直线所截, 两条直线平行是同位角相等的充要条件
(1)p?????,??????????, p是????的必要不充分条件
?
(2)?????????,??????????, 即????????? ,p是????的充要条件
?
(3)p?????,??????????, p是????的必要不充分条件
?
(4)????????? ?????????, p是????的充分不必要条件
?
例2用充分条件必要条件的语言表述下面的命题
(1)若a=-b,则|a|=|b|
(2)若点C是线段AB的中点则AC=BC;
(3)当ac<0时,一元二次方程ax2+bx+c=0有两个不相等的实数根解
(1)“a=-b”是“|a|=b|”的充分不必要条件;
(2)“点C是线段AB的中点”是“AC=BC“的充分不必要条件;
(3)“ac<0”是“一元二次方程ax2+bx+c=0有两个不相等的实数根”的充分不必要条件
P16例2巩固复习
1.下列各题中试判断p是q的什么条件。
(1)????:????????=????????????????≠0,????:????2=????????;
(2)对于反比例函数????=????????,????>0,????>0,?q:y值随x值的增大而减小;
(3)p:函数的图象关于y轴对称,q:函数????=????2。
2.用充分条件或必要条件的语言表述下面的定理
(1)在一个平面内,垂直于同一条直线的两条直线平行;
(2) 若a>b, c<0 ,则 ac
(4)如果????1,????2是一元二次方程????????2+????????+????=0(????≠0)的两个实数根,那么????1+????2=?????????。
?
(1)????????? ?????????, p是????的充分不必要条件
?
(2)?????????,??????????, 即????????? ,p是????的充要条件
?
(3)p?????,??????????, p是????的必要不充分条件
?
(1)在一个平面内,
“两条直线垂直于同一条直线”
是“这两条直线平行"的充要条件;
(2)“a>b, c<0”是“ac
(4)已知方程????????2+????????+????=0(????≠0),则“????1,????2是方程的两个实数根”是“????1+????2=?????????”的充分不必要条件
?
P16练习1、2巩固复习
例3在下列各题中,试判断是p是q的什么条件
(1)p:A?B, q:A∩B=A;
(2)p:a=b,q:|a|=|bl;
(3)p:四边形的对角线相等,q:四边形是平行四边形
?
(1)?????????,??????????, 即????????? ,p是????的充要条件
?
(2)????????? ?????????, p是????的充分不必要条件
?
(3)p?????,??????????, p是????的即不充分又不必要条件
?
P17例3巩固复习
1.用“充分条件”“必要条件”或“充要条件”填空:
(1)“????∈N”是“????∈Q”的 。
(2)“????=2”是“????2?3????+2=0”的 。
(3) “????>2”是“????>3”的 。
(4)“????????>0”是“????????>0”的 。
2.下列各题中,试判断p是q的什么条件。
(1)????:1????<1,????:????>1;
(2)?????:四边形的对角线相等,????:四边形是矩形;
(3)?????:一元二次函数????=????????2+????(????≠0),?????:一元二次函数的图象关于y轴对称。
3.已知集合????=????|????=2????,????∈Z,????=????|????=4????+2,????∈Z,设????:????∈????,????:????∈????,试判断p是q的什么条件,q是p的什么条件。
?
(3)????????? ?????????, p是????的充分不必要条件
?
(1)p?????,??????????, p是????的必要不充分条件
?
(2) 充分不必要条件;
(1) 的充分不必要条件
必要不充分条件
充要条件
(2)p?????,??????????, p是????的必要不充分条件
?
3. p?????,??????????, p是????的必要不充分条件,????是p的充分不必要条件
?
P18练习1、2、3巩固复习
1.请在“充分条件”“必要条件”“充要条件”“既不是充分条件也不是必要条件"中选择一个最恰当的,填空:
(1)当?????????时,“????∈????”是“????∈????”的 ;
(2)“????是偶数,?????是偶数”是“???????? 是偶数”的 ;
(3)“?????????”是“????∪????=????” 的 ;
(4)“????????>0”是“????>0,且????>0”的 ;
(5“整数????能被3整除"是“整数????能被6整除”的 ;
(6)“????-2=0”是“(???? +2)(????? -2)=0”的 ;
(7)“????=?”是“????∩????=?”的 ;
(8)“????=????”是“????2+????2≥2????????”的 。
2.判断下列说法是否正确:
(1) “????∈N”是“????∈Z”的充分条件;
(2)“????b=0”是“a2+b2=0”的充要条件:
(3)“两个三角形全等”是“两个三角形相似”的充分条件;
(4)“两个三角形中有两边及其中一边的对角分别相等”是“两个三角形全等”的充要条件。
?
充分不必要条件;
充分不必要条件
必要不充分条件
充要条件
必要不充分条件
充分不必要条件;
充分不必要条件;
充分不必要条件;
正确
正确
错误,必要条件
错误,必要条件
P22习A组1、2巩固复习
例1 .设集合A={1,????2,-2} ,集合B={2,4},则“????=2”是“????∩????=4”的( )条件.
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
?
【解】若a=2,则A={1,4,-2},A∩B=4,满足充分条件要求;
?
若A∩B=4,则????2=4,解得a=2或a=?2?,不满足必要条件要求;
?
所以“????=2”是“????∩????=4”的充分不必要条件,选A
?
A
已知集合M={x|x<-3或x>5},P={x|(x-a)·(x-8)≤0} ,
则M∩P={x|5
5
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
