人教版 八下 第十七章 第一节 勾股定理 教学设计
文档属性
| 名称 | 人教版 八下 第十七章 第一节 勾股定理 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 816.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 10:14:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
《勾股定理》教学设计
授课类型 新授课 教材课本 人民教育出版社八年级下册数学
授课年级 初二 授课内容 第十七章 第一节 《勾股定理》
目录
课标解读
教材分析
学情分析
教学目标
教学重难点
教学方法
教学过程
课标解读
课标要求是探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题。本节课重点落实在“勾股定理”这个知识点。
行为动词是“探索”和“运用”,要求学生能够独立或合作探究出勾股定理的证明过程,发现直角三角形的三边的数量关系,并能运用适当的方法解决实际问题。
行为水平是学习本节课内容后,学生应达到理解勾股定理的概念,体会勾股定理再发现过程,能够运用勾股定理解决一些简单的实际问题。
因此,根据课标的要求,本节课借助课件,几何画板等,引导学生发现勾股定理,掌握证明勾股定理的方法,能够运用勾股定理解决一些生活实际问题。
教材分析
本节课的内容主要是探究勾股定理,并且进行简单的利用,在本节课之前,已经安排了三角形三边关系、完全平方公式、直角三角形、二次根式等的运算。本课也是学生今后学习勾股逆定理、四边形及其他相关内容的基础。
学情分析
基础知识:学生已经学习了三角形三边关系并且通过对直角三角形、等腰三角形有关的知识积累,已经具有了研究特殊三角形的方法和初步的经验。
认知水平与能力:八年级的学生模仿力较强,思维多依赖具体直观的形象,对几何证明的内容有一定的难度。
教学目标
理解和掌握勾股定理的内容
经历勾股定理的探究过程,理解勾股定理的证明方法。
运用勾股定理解决一些实际问题
教学重难点
重点:勾股定理的探索过程及应用
难点:勾股定理的证明
教学方法
启发讲授
引导发现
探究讨论
教学过程
环节一:课堂导入,激发兴趣
教师活动 学生活动 设计意图
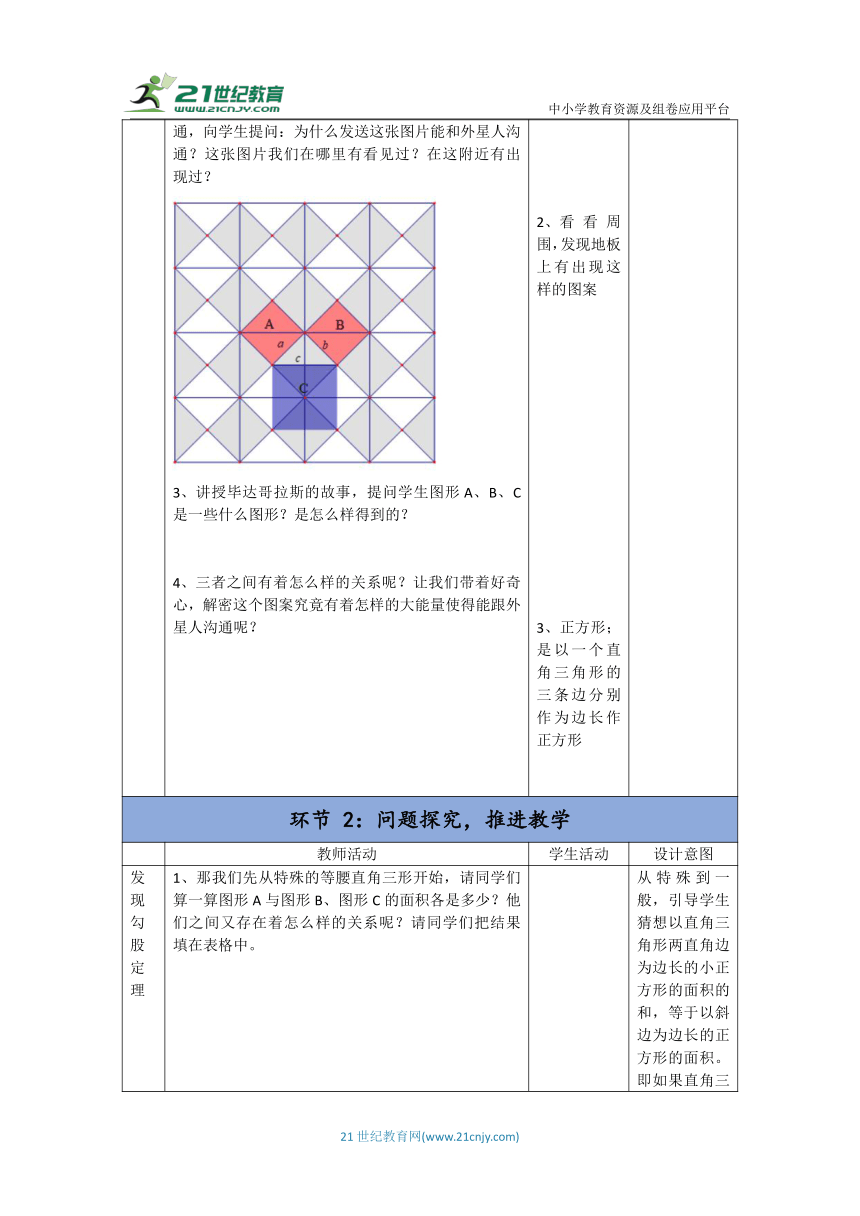
创建情景 1、向学生展示浩瀚无边的宇宙,并提问:在这浩瀚无边的宇宙中,如果有外星人的存在,我们怎么样才能跟他们沟通得上呢? 提出向太空发出这样的图片就能够和外星人沟通,向学生提问:为什么发送这张图片能和外星人沟通?这张图片我们在哪里有看见过?在这附近有出现过? 讲授毕达哥拉斯的故事,提问学生图形A、B、C是一些什么图形?是怎么样得到的? 三者之间有着怎么样的关系呢?让我们带着好奇心,解密这个图案究竟有着怎样的大能量使得能跟外星人沟通呢? 观察图片,思考有什么办法能够和外星人沟通。 看看周围,发现地板上有出现这样的图案 正方形;是以一个直角三角形的三条边分别作为边长作正方形 设置悬念,引入情境,激发学生的学习兴趣。
环节 2:问题探究,推进教学
教师活动 学生活动 设计意图
发现勾股定理 1、那我们先从特殊的等腰直角三形开始,请同学们算一算图形A与图形B、图形C的面积各是多少?他们之间又存在着怎么样的关系呢?请同学们把结果填在表格中。 提问:图形A 和图形B的面积怎么算呢? 提问:那正方形C又怎么算?能直接利用边长乘边长的公式算吗?如果不能,我们应该怎么算? 补充:除了能用补的方法,还可以用分割法,即将一个正方形分割成四个直角三角形,从而算出正方形的面积。 提问:说出表格中的答案。 那我们一起来看看如果在一般直角形中,三个正方形的面积又有着怎么样的关系呢?利用刚刚提到的方法,算一算以下左图以及右图的正方形的面积,并将答案填入下表格中 请同学们仔细观察我们刚刚算出来的两份表格,有没有发现了什么?A的面积、B的面积和C的面积之间存在着什么关系? 那正方形A、正方形B与正方形C是怎么来的? 所以我们猜想以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积。 即如果直角三角形的两直角边长分别为a,b,斜边长为c,用数学语言表示就是 利用正方形面积公式=边长乘边长,能够算出正方形A和正方形B 不能,可以将正方形补充成一个大的正方形,减去空白的地方,从而算出正方形C的面积。 5、说出表格中的答案 6、观察左右两图的形状,并计算其面积,将结果填入表格中。 由一个直角三角形以其三条边为边长向外做的正方形。 从特殊到一般,引导学生猜想以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积。即如果直角三角形的两直角边长分别为a,b,斜边长为c,那么
证明勾股定理 上面我们只是简单的猜想一下,并不是严谨的证明,那接下来我们运用严谨的数学方法对我们的猜想进行证明。 现在桌面上有四个一模一样的直角三角形,我们假设两直角边分别为a,b,斜边为c,请同学们计算一下四个直角三角形的面积之和为多少? 请同学们利用这四个直角三角形拼接成一个大的正方形(用几何画板演示) 那这个大的正方形的边长是多少呢?面积又是多少? 拼接前与拼接后的面积会不一样吗?如果一样,我们能得到什么样式子呢? 即如果直角三角形的两直角边长分别为a,b,斜边长为c,用数学语言表示就是。即我们的猜想是正确的,我们称这个命题为勾股定理。 1、4ab 拼接成一个大的正方形 这个大的正方形的边长是c;面积是 一样的, 利用几何画板的演示,以及面积相等证明勾股定理的存在。
例题讲解 给出一个直角形的其中两条边的边长,求另外一条的边长。 提升到日常生活情境中,利用勾股定理解决日常生活问题。 (问题串: ①这块木板能不能横着或者竖着通过这个门框呀?为什么?那能用怎么样的形式使得木板通过门框呢? ②怎么样才能判定这块木板能够斜着的通过这个门框呢? ③门框内最大长度是哪一条边?这个长度怎么求?) 利用勾股定理,算出答案。 回答问题串,利用勾股定理求得门框内最大的长度,并将其与木板的最短的边最对比,从而得出结果,解决实际问题。 由易到难的设置题目,使学生体会到勾股定理在题目中、在生活中的使用,知道在什么的情况下会使用勾股定理。
环节3:课堂小结
教师活动 学生活动 设计意图
小结 以提问的形式,检测学生对本节课的知识点是否掌握好,是否真正理解到勾股定理的概念。 跟着老师总结回顾本节课所学知识,自我检查对本节课的知识掌握程度 回顾本节课所学知识,建立明确的知识框架,有助于学生理解与掌握,加深学生的印象。
21世纪教育网(www.21cnjy.com)
《勾股定理》教学设计
授课类型 新授课 教材课本 人民教育出版社八年级下册数学
授课年级 初二 授课内容 第十七章 第一节 《勾股定理》
目录
课标解读
教材分析
学情分析
教学目标
教学重难点
教学方法
教学过程
课标解读
课标要求是探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题。本节课重点落实在“勾股定理”这个知识点。
行为动词是“探索”和“运用”,要求学生能够独立或合作探究出勾股定理的证明过程,发现直角三角形的三边的数量关系,并能运用适当的方法解决实际问题。
行为水平是学习本节课内容后,学生应达到理解勾股定理的概念,体会勾股定理再发现过程,能够运用勾股定理解决一些简单的实际问题。
因此,根据课标的要求,本节课借助课件,几何画板等,引导学生发现勾股定理,掌握证明勾股定理的方法,能够运用勾股定理解决一些生活实际问题。
教材分析
本节课的内容主要是探究勾股定理,并且进行简单的利用,在本节课之前,已经安排了三角形三边关系、完全平方公式、直角三角形、二次根式等的运算。本课也是学生今后学习勾股逆定理、四边形及其他相关内容的基础。
学情分析
基础知识:学生已经学习了三角形三边关系并且通过对直角三角形、等腰三角形有关的知识积累,已经具有了研究特殊三角形的方法和初步的经验。
认知水平与能力:八年级的学生模仿力较强,思维多依赖具体直观的形象,对几何证明的内容有一定的难度。
教学目标
理解和掌握勾股定理的内容
经历勾股定理的探究过程,理解勾股定理的证明方法。
运用勾股定理解决一些实际问题
教学重难点
重点:勾股定理的探索过程及应用
难点:勾股定理的证明
教学方法
启发讲授
引导发现
探究讨论
教学过程
环节一:课堂导入,激发兴趣
教师活动 学生活动 设计意图
创建情景 1、向学生展示浩瀚无边的宇宙,并提问:在这浩瀚无边的宇宙中,如果有外星人的存在,我们怎么样才能跟他们沟通得上呢? 提出向太空发出这样的图片就能够和外星人沟通,向学生提问:为什么发送这张图片能和外星人沟通?这张图片我们在哪里有看见过?在这附近有出现过? 讲授毕达哥拉斯的故事,提问学生图形A、B、C是一些什么图形?是怎么样得到的? 三者之间有着怎么样的关系呢?让我们带着好奇心,解密这个图案究竟有着怎样的大能量使得能跟外星人沟通呢? 观察图片,思考有什么办法能够和外星人沟通。 看看周围,发现地板上有出现这样的图案 正方形;是以一个直角三角形的三条边分别作为边长作正方形 设置悬念,引入情境,激发学生的学习兴趣。
环节 2:问题探究,推进教学
教师活动 学生活动 设计意图
发现勾股定理 1、那我们先从特殊的等腰直角三形开始,请同学们算一算图形A与图形B、图形C的面积各是多少?他们之间又存在着怎么样的关系呢?请同学们把结果填在表格中。 提问:图形A 和图形B的面积怎么算呢? 提问:那正方形C又怎么算?能直接利用边长乘边长的公式算吗?如果不能,我们应该怎么算? 补充:除了能用补的方法,还可以用分割法,即将一个正方形分割成四个直角三角形,从而算出正方形的面积。 提问:说出表格中的答案。 那我们一起来看看如果在一般直角形中,三个正方形的面积又有着怎么样的关系呢?利用刚刚提到的方法,算一算以下左图以及右图的正方形的面积,并将答案填入下表格中 请同学们仔细观察我们刚刚算出来的两份表格,有没有发现了什么?A的面积、B的面积和C的面积之间存在着什么关系? 那正方形A、正方形B与正方形C是怎么来的? 所以我们猜想以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积。 即如果直角三角形的两直角边长分别为a,b,斜边长为c,用数学语言表示就是 利用正方形面积公式=边长乘边长,能够算出正方形A和正方形B 不能,可以将正方形补充成一个大的正方形,减去空白的地方,从而算出正方形C的面积。 5、说出表格中的答案 6、观察左右两图的形状,并计算其面积,将结果填入表格中。 由一个直角三角形以其三条边为边长向外做的正方形。 从特殊到一般,引导学生猜想以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积。即如果直角三角形的两直角边长分别为a,b,斜边长为c,那么
证明勾股定理 上面我们只是简单的猜想一下,并不是严谨的证明,那接下来我们运用严谨的数学方法对我们的猜想进行证明。 现在桌面上有四个一模一样的直角三角形,我们假设两直角边分别为a,b,斜边为c,请同学们计算一下四个直角三角形的面积之和为多少? 请同学们利用这四个直角三角形拼接成一个大的正方形(用几何画板演示) 那这个大的正方形的边长是多少呢?面积又是多少? 拼接前与拼接后的面积会不一样吗?如果一样,我们能得到什么样式子呢? 即如果直角三角形的两直角边长分别为a,b,斜边长为c,用数学语言表示就是。即我们的猜想是正确的,我们称这个命题为勾股定理。 1、4ab 拼接成一个大的正方形 这个大的正方形的边长是c;面积是 一样的, 利用几何画板的演示,以及面积相等证明勾股定理的存在。
例题讲解 给出一个直角形的其中两条边的边长,求另外一条的边长。 提升到日常生活情境中,利用勾股定理解决日常生活问题。 (问题串: ①这块木板能不能横着或者竖着通过这个门框呀?为什么?那能用怎么样的形式使得木板通过门框呢? ②怎么样才能判定这块木板能够斜着的通过这个门框呢? ③门框内最大长度是哪一条边?这个长度怎么求?) 利用勾股定理,算出答案。 回答问题串,利用勾股定理求得门框内最大的长度,并将其与木板的最短的边最对比,从而得出结果,解决实际问题。 由易到难的设置题目,使学生体会到勾股定理在题目中、在生活中的使用,知道在什么的情况下会使用勾股定理。
环节3:课堂小结
教师活动 学生活动 设计意图
小结 以提问的形式,检测学生对本节课的知识点是否掌握好,是否真正理解到勾股定理的概念。 跟着老师总结回顾本节课所学知识,自我检查对本节课的知识掌握程度 回顾本节课所学知识,建立明确的知识框架,有助于学生理解与掌握,加深学生的印象。
21世纪教育网(www.21cnjy.com)
