思维拓展:圆综合-数学六年级上册北师大版(含答案)
文档属性
| 名称 | 思维拓展:圆综合-数学六年级上册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 19:48:56 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
思维拓展:圆综合-数学六年级上册北师大版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共18分)
1.大圆的半径等于小圆的直径,大圆面积是小圆面积的( )倍。
A.2 B.4 C.8 D.16
2.如图中阴影部分的面积是9平方厘米,图中圆环的面积是( )平方厘米。
A.18.84 B.56.52 C.81 D.28.26
3.外圆半径为R,内圆半径为r的一个圆环的面积等于( )。
A.π(R -r ) B.π(R-r) C.2πR-2πr D.π(R+r)
4.比较下列图形中的阴影部分,下面说法正确的是( )。
A.甲图阴影部分面积大。 B.乙图阴影部分面积大。
C.一样大 D.无法比较
5.如图中,阴影部分面积是空白部分面积的( )。
A. B. C. D.
6.如图,把正方形桌面的四边撑起,就成了一张圆面桌子。经过测量,圆面桌子的面积是π平方米,那么正方形桌面的面积为( )平方米。
A.1 B.2 C.π D.π
二、填空题
7.2020年9月28日山西省鼓乐大赛决赛在新绛举行,工人师傅要用镀锌管和喷绘布制作一面鼓面直径为4m的大鼓模型。要在一张长方形喷绘布上裁出这样的两个鼓面,长方形喷绘布的长至少是( )米,宽至少是( )米。每个鼓面的面积是( )平方米。
8.时针长3cm,分针长6cm,经过三小时后,时针针尖走了( )cm,时针扫过的面积是( )。分针针尖走了( )cm,分针扫过的面积是( )。
9.从下面的长方形纸上剪一个面积最大的圆,这个圆的面积是( )cm2。
10.某钟表的分针长8厘米,时针长6厘米。从中午12时到下午3时,分针针尖走过了( )厘米,时针扫过的面积是( )平方厘米。
11.一张圆片对折3次后得到一个扇形,它的面积是圆片面积的( ),圆心角是( )。
12.如图,甲、乙两只蚂蚁分别从A、B两点出发,沿半圆爬到C、D处,它们爬过的路程相差( )厘米。
三、判断题
13.如果大圆周长是小圆周长的4倍,那么小圆面积是大圆面积的。( )
14.大小两个不同的圆,它们的圆周率也不同。( )
15.画圆时,如果圆规两脚之间的距离是2厘米,这个圆的周长和面积一样大。( )
16.如果一个圆的周长是2πr厘米,那么半圆的周长是πr厘米。( )
17.一个圆的半径变为原来的,它的周长和面积也都变为原来的。( )
四、图形计算
18.求下列阴影部分的面积。
五、解答题
19.小亮骑一辆自行车,如果车轮的外直径是0.6m,车轮每分钟转动120圈,那么5分钟可以行多少米?
20.爷爷家新买了一张折叠餐桌,收起来是一个正方形,展开后是一个直径为1.2米的圆(如图所示),桌面可以收起来的部分的面积是多少平方米?(结果保留两位小数)
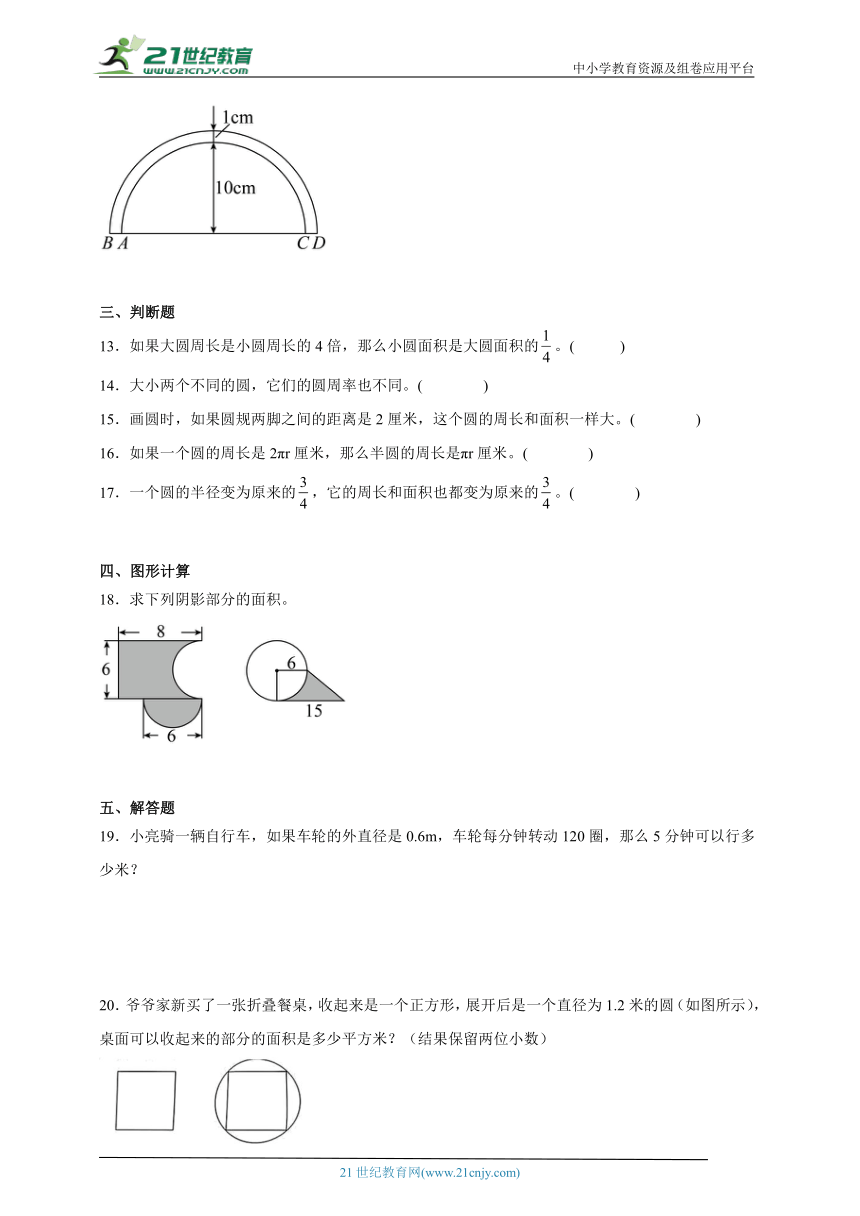
21.张红同学计划用12.56米长的篱笆靠墙围一个半圆形的兔舍(靠墙一边不围篱笆),这个半圆形兔舍的面积是多少?
22.如下图是公园中的一个花瓣形状的门洞,这个门洞的四周是4个直径相等的半圆。这个门洞的面积是多少平方米?
23.下图中圆的周长是62.8厘米,圆的面积正好与长方形的面积相等,你能求出图中阴影部分的面积吗?
24.如图,把4个半径为5厘米的圆柱形塑料管用绳子捆扎在一起。
(1)一根塑料管的横截面(如图中阴影部分)面积是多少?
(2)图中的线段的长度相当于圆的( ),曲线b的长度是( )厘米。打结部分绳长25厘米,那么捆扎这4个塑料管需用多少厘米的绳子?
参考答案:
1.B
【分析】假设小圆的半径是1,则小圆的直径:1×2=2,则大圆的半径是2,根据圆的面积公式:π×半径2,分别求出大圆和小圆的面积,用大圆面积除以小圆面积即可。
【详解】假设小圆的半径是1,则大圆的半径:1×2=2
小圆面积:π×1×1=π
大圆面积:2×2×π=4π
4π÷π=4
故答案选:B
【点睛】本题主要考查圆的面积公式,熟练掌握圆的面积公式并灵活运用。
2.D
【分析】如图所示,设大圆半径为R,小圆的半径为r,则图中大正方形边长为R,小正方形的边长为r,则阴影部分的面积=R2-r2,根据圆环面积=π(R2-r2),据此解答即可。
【详解】设大圆半径为R,小圆半径为r。
则阴影部分的面积=R2-r2=9平方厘米。
3.14×(R2-r2)
=3.14×9
=28.26(平方厘米)
即圆环面积是28.26平方厘米。
故答案为:D
【点睛】解答此题的关键:用大圆和小圆的半径表示出阴影部分的面积,进而求出圆环面积。
3.A
【分析】根据圆环面积=外圆面积-内圆面积,即可解答。
【详解】圆环面积=πR -πr =π(R -r )。
故答案为:A
【点睛】本题考查圆环的面积,根据公式解答。
4.C
【分析】根据题意可知,甲图的阴影部分的面积是边长为10的正方形面积减去4个半径是(10÷4)圆的面积;乙图是一个边长是10的正方形面积减去半径为(10÷2)的圆的面积;根据正方形面积公式:边长×边长;圆的面积公式:π×半径2,代入数据,求出阴影部分的面积,再进行比较,即可解答。
【详解】甲图阴影部分面积:
10×10-3.14×(10÷4)2×4
=100-3.14×6.25×4
=100-19.625×4
=100-78.5
=21.5
乙图阴影部分面积:
10×10-3.14×(10÷2)2
=100-3.14×25
=100-78.5
=21.5
21.5=21.5
甲图阴影部分面积和乙图阴影部分面积一样大。
故答案选:C
【点睛】本题考查正方形面积公式、圆的面积公式的应用,关键是熟记公式。
5.B
【分析】观察图形可知,阴影部分半圆的半径是空白半圆半径的一半,设阴影部分半圆的半径为1,则空白半圆的半径为1×2=2,根据圆的面积公式:π×半径2,求出阴影部分半圆的面积和空白半圆的面积,再用阴影部分面积除以空白半圆面积,即可解答。
【详解】设阴影部分半圆的半径为1,则空白半圆半径为:1×2=2
阴影部分半圆面积:π×12×=π
空白半圆面积:π×(1×2)2×
=π×4×
=2π
π÷2π=×=
阴影部分的面积是空白部分面积的。
故答案选:B
【点睛】本题考查圆的面积公式的应用,关键是熟记公式,以及求一个数占另一个数的几分之几。
6.B
【分析】
观察图可知,正方形的面积等于两个等腰直角三角形面积组成,三角形的斜边是圆的直径,斜边对应的高是圆的半径,根据三角形的面积=底×高÷2,半径表示为r,一个等腰直角三角形的面积可表示为2r×r÷2,也就是r2,2个等腰直角三角形的面积则表示为2r2;根据圆面积公式:S=πr2,用π÷π即可求出r2是多少,再乘2即可求出正方形的面积。
【详解】如图:
要使正方形的面积最大,正方形的对角线为圆的直径,
设圆的半径为r,圆的面积为πr2,正方形的面积为:2r2
π×r2=π
解:r2=π÷π
r2=1
所以正方形的面积为:2×1=2(平方米)
正方形的面积是2平方米。
故答案为:B
【点睛】本题主要考查了正方形和圆的关系,熟记相关公式是解答本题的关键。
7. 8 4 12.56
【分析】根据题意可知,长方形喷绘布的长是圆的直径的2倍,宽是圆的直径,根据圆的面积S=πr2求出圆的面积。
【详解】长方形喷绘布的长至少是4×2=8米,宽至少是4米。
每个鼓面的面积:
3.14×(4÷2)2
= 3.14×4
=12.56(平方米)
【点睛】重点考查了圆的面积的实际应用,计算时要认真。
8. 4.71 7.065cm2 113.04 339.12cm2
【分析】经过三小时,时针针尖走了3÷12=圆的周长,时针扫过的面积是圆的面积。又因时针长3厘米,即时针所经过的圆的半径是3厘米,从而利用圆的周长、面积公式解答即可;经过三小时,分针转了三圈,又因分针长6厘米,即分针所经过的圆的半径是6厘米,从而利用圆的周长、面积公式求解即可。
【详解】3.14×3×2×(3÷12)
=18.84×
=4.71(厘米)
3.14×32×
=28.26×
=7.065(平方厘米)
3.14×6×2×3
=3.14×36
=113.04(厘米)
3.14×62×3
=3.14×36×3
=113.04×3
=339.12(平方厘米)
【点睛】本题主要考查圆的周长、面积公式的实际应用,解题时要明确经过三小时,时针旋转圆,分针旋转3圈。
9.50.24
【分析】根据题意,长方形内画最大的圆,圆的直径等于长方形的宽;根据圆的面积公式:π×半径2,代入数据,即可解答。
【详解】3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(cm2)
【点睛】本题考查圆的面积公式的应用;关键明确长方形内画最大的圆,圆的直径等于长方形的宽。
10. 150.72 28.26
【分析】从中午12时到下午3时,分针旋转了3圈,时针旋转了3大格,旋转一大格是30°,由此可知时针旋转了3×30°=90°,根据圆的周长C=πd,圆的面积S=πr2,解答即可。
【详解】3.14×(2×8)×3
=3.14×16×3
=50.24×3
=150.72(厘米)
分针针尖走过了150.72厘米。
3.14×62×
=113.04×
=28.26(平方厘米)
时针扫过的面积是28.26平方厘米。
【点睛】此题考查了圆的周长和面积的相关计算,掌握公式并能灵活运用是解题关键。
11. 45°
【分析】根据题意,一张圆片对折3次,就是把这根圆片平均分成8份,求一份占圆片的几分之几,把圆片的面积看作单位“1”,用1÷8,即可;圆心角是360°,再用圆心角360°×一个扇形占圆片面积的分率,即可解答。
【详解】1÷8=
360°×=45°
【点睛】利用分数的意义以及求一个数的几分之几是多少。
12.3.14
【分析】蚂蚁走过的路程刚好是圆周长的一半,圆的周长=2πr,则周长的一半=πr,代入不同的半径,求出两个路程的长度作差即可。
【详解】大半径:10+1=11(厘米)
3.14×11-3.14×10
=34.54-31.4
=3.14(厘米)
它们爬过的路程相差3.14厘米。
【点睛】此题主要考查圆的周长公式,熟练掌握它的公式并灵活运用。
13.×
【分析】圆的周长=2π×半径,如果大圆的周长是小圆周长的4倍,则大圆的半径就是小圆半径的4倍。设小圆半径为r,则大圆半径为4r,根据圆的面积公式:π×半径2,即可解答。
【详解】大圆周长是小圆周长的4倍,则大圆半径是小圆半径的4倍。
设:小圆半径为r,则大圆半径为4r。
小圆面积为:πr2
大圆面积为:π×(4r)2=16πr2
πr2÷16πr2=
大圆周长是小圆周长的4倍,那么小圆面积是大圆面积的。
故答案为:×
【点睛】本题考查圆的周长公式、面积公式的应用,关键是熟记公式,灵活运用。
14.×
【分析】任意一个圆的周长与它的直径的比值都是一个固定的数,我们把它叫做圆周率,据此解答即可。
【详解】根据圆周率的含义可知:大小两个圆,它们的圆周率都相等,故本题说法错误。
【点睛】此题考查对圆周率的认识,圆周率是一个固定不变的数。
15.×
【分析】半径决定圆的大小,画圆时,圆规两脚之间的距离等于所画圆的半径。根据题意,圆的周长单位是厘米,面积单位是平方厘米,长度单位和面积单位是无法比较大小的,据此判断即可。
【详解】由题意可知:圆规两脚之间的距离是2厘米,即半径是2厘米,所画的圆周长单位是厘米,面积单位是平方厘米,周长和面积不能比较大小。原题说法错误。
故答案为:×
【点睛】解答此题的关键是确定:长度单位和面积单位是无法比较大小的。
16.×
【分析】半圆的周长=圆周长的一半+直径,据此判断。
【详解】如果一个圆的周长是2πr厘米,那么半圆的周长是2πr÷2+2r=πr+2r厘米。原题说法错误。
故答案为:×
【点睛】此题考查了圆周长的相关知识,注意半圆的周长记得加一个直径的长度。
17.×
【分析】圆的周长=2πr,圆的面积=πr2 ,圆的半径变为原来的,圆的周长也变为原来的,圆的面积则会缩小到原来的的平方。由此即可解答。
【详解】一个圆的半径缩小到原来的,它的周长也缩小到原来的,面积缩小到原来的
故答案为:×。
【点睛】此题考查了圆的半径与周长、面积的关系,理解掌握公式是解答的关键。
18.48;34.74
【分析】第一个图形将扇形通过顺时针旋转,可得阴影部分的面积相当于一个长方形的面积,长是8,宽是6,根据长方形的面积=长×宽,代入数据解答。
第二个图形的阴影面积=梯形的面积-扇形的面积,梯形的上底是6、下底是15、高是6,根据梯形的面积=(上底+下底)×高÷2,代入数据即可求出梯形的面积,扇形的面积相当于半径是6的圆面积的,根据圆面积公式:S=πr2以及分数乘法的意义,用3.14×62×即可求出扇形的面积,进而用减法求出阴影部分的面积。
【详解】8×6=48
第一个阴影部分的面积是48;
(6+15)×6÷2
=21×6÷2
=63
3.14×62×
=3.14×36×
=28.26
63-28.26=34.74
阴影部分的面积是34.74。
19.1130.4米
【分析】车轮转一圈的长度就是车轮的周长,根据圆的周长=πd求出车轮转一圈的长度,再乘每分钟转的圈数求出车轮1分钟前进的速度,最后乘时间5分钟即可求出路程。
【详解】0.6×3.14×120×5
=1.884×120×5
=226.08×5
=1130.4(米)
答:5分钟可以行1130.4米。
【点睛】本题考查圆的周长的应用,要理解车轮转一圈的长度就是车轮的周长。
20.0.41平方米
【分析】桌面可以收起来的部分的面积=圆的面积-正方形的面积;圆的面积=πr2,圆的直径刚好是正方形的对角线,正方形的面积=对角线×对角线÷2,直接代入数据计算即可。
【详解】圆的面积:
3.14×(1.2÷2)2
=3.14×0.62
=3.14×0.36
=1.1306(平方米)
正方形的面积:
1.2×1.2÷2
=1.44÷2
=0.72(平方米)
收起来的面积:
1.1306-0.72=0.4106≈0.41(平方米)
答:桌面可以收起来的部分的面积是0.41平方米。
【点睛】此题主要考查圆的面积公式,掌握正方形面积的求法也是解题的关键。
21.25.12平方米
【分析】观察题意可知,篱笆的长度相当于圆周长的一半,根据圆周长公式:C=2πr,用2×12.56÷2÷3.14即可求出半径,也就是4米,再根据圆面积公式:S=πr2,用3.14×42÷2即可求出半圆的面积。
【详解】2×12.56÷2÷3.14=4(米)
3.14×42÷2
=3.14×16÷2
=25.12(平方米)
答:这个半圆形兔舍的面积是25.12平方米。
【点睛】本题考查了圆周长公式、圆面积公式的灵活应用,要熟练掌握相关公式。。
22.10.28平方米
【分析】由图可知,门洞的面积=直径是2米的圆的面积×2+边长是2米的正方形的面积;根据圆的半径:r=d÷2,圆的面积:S=π,正方形的面积:S=a×a;据此代入数据解答。
【详解】由分析得:
=3.14×1×2+4
=6.28+4
=10.28(平方米)
答:这个门洞的面积是10.28平方米。
【点睛】此题主要考查组合图形的面积,关键是把不规则图形转化成规则图形,利用规则图形的面积公式计算。
23.235.5平方厘米
【分析】通过分析图形可知,阴影部分的面积=长方形面积-圆面积,因此先利用圆的周长公式:求出圆的半径,然后通过圆的面积公式:求出圆的面积,已知圆的面积=长方形面积,由此即可解答。
【详解】圆的半径:62.8÷3.14÷2
=20÷2
=10(厘米)
长方形面积=圆的面积=3.14×10=314(平方厘米)
314-314÷4
=314-78.5
=235.5(平方厘米)
答:阴影部分的面积是235.5平方厘米。
【点睛】此题主要考查了学生对圆的周长和面积公式的理解与灵活应用解题能力。
24.(1)78.5平方厘米;(2)直径;7.85;96.4厘米
【分析】(1)一根塑料管的横截面面积是半径为5cm的圆的面积,然后再根据圆的面积公式S=πr2进行解答。
(2)图中的线段的长度相当于圆的直径,曲线b的长度相当于半径为5cm的圆的周长;捆扎这4个塑料管的绳子长度=半径为5cm的圆的周长+圆的直径×4+打结部分绳长;然后再根据圆的周长公式C=2πr,d=2r进行解答。
【详解】(1)3.14×52
=3.14×25
=78.5(平方厘米)
答:一根塑料管的横截面(如图中阴影部分)面积是78.5平方厘米。
(2)2×3.14×5×
=6.28×5×
=31.4×
=7.85(厘米)
即图中的线段的长度相当于圆的直径,曲线b的长度是7.85厘米。
2×3.14×5+2×5×4+25
=6.28×5+10×4+25
=31.4+40+25
=71.4+25
=96.4(厘米)
答:那么捆扎这4个塑料管需用96.4厘米的绳子。
【点睛】考查了圆的面积公式和周长公式的运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:圆综合-数学六年级上册北师大版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共18分)
1.大圆的半径等于小圆的直径,大圆面积是小圆面积的( )倍。
A.2 B.4 C.8 D.16
2.如图中阴影部分的面积是9平方厘米,图中圆环的面积是( )平方厘米。
A.18.84 B.56.52 C.81 D.28.26
3.外圆半径为R,内圆半径为r的一个圆环的面积等于( )。
A.π(R -r ) B.π(R-r) C.2πR-2πr D.π(R+r)
4.比较下列图形中的阴影部分,下面说法正确的是( )。
A.甲图阴影部分面积大。 B.乙图阴影部分面积大。
C.一样大 D.无法比较
5.如图中,阴影部分面积是空白部分面积的( )。
A. B. C. D.
6.如图,把正方形桌面的四边撑起,就成了一张圆面桌子。经过测量,圆面桌子的面积是π平方米,那么正方形桌面的面积为( )平方米。
A.1 B.2 C.π D.π
二、填空题
7.2020年9月28日山西省鼓乐大赛决赛在新绛举行,工人师傅要用镀锌管和喷绘布制作一面鼓面直径为4m的大鼓模型。要在一张长方形喷绘布上裁出这样的两个鼓面,长方形喷绘布的长至少是( )米,宽至少是( )米。每个鼓面的面积是( )平方米。
8.时针长3cm,分针长6cm,经过三小时后,时针针尖走了( )cm,时针扫过的面积是( )。分针针尖走了( )cm,分针扫过的面积是( )。
9.从下面的长方形纸上剪一个面积最大的圆,这个圆的面积是( )cm2。
10.某钟表的分针长8厘米,时针长6厘米。从中午12时到下午3时,分针针尖走过了( )厘米,时针扫过的面积是( )平方厘米。
11.一张圆片对折3次后得到一个扇形,它的面积是圆片面积的( ),圆心角是( )。
12.如图,甲、乙两只蚂蚁分别从A、B两点出发,沿半圆爬到C、D处,它们爬过的路程相差( )厘米。
三、判断题
13.如果大圆周长是小圆周长的4倍,那么小圆面积是大圆面积的。( )
14.大小两个不同的圆,它们的圆周率也不同。( )
15.画圆时,如果圆规两脚之间的距离是2厘米,这个圆的周长和面积一样大。( )
16.如果一个圆的周长是2πr厘米,那么半圆的周长是πr厘米。( )
17.一个圆的半径变为原来的,它的周长和面积也都变为原来的。( )
四、图形计算
18.求下列阴影部分的面积。
五、解答题
19.小亮骑一辆自行车,如果车轮的外直径是0.6m,车轮每分钟转动120圈,那么5分钟可以行多少米?
20.爷爷家新买了一张折叠餐桌,收起来是一个正方形,展开后是一个直径为1.2米的圆(如图所示),桌面可以收起来的部分的面积是多少平方米?(结果保留两位小数)
21.张红同学计划用12.56米长的篱笆靠墙围一个半圆形的兔舍(靠墙一边不围篱笆),这个半圆形兔舍的面积是多少?
22.如下图是公园中的一个花瓣形状的门洞,这个门洞的四周是4个直径相等的半圆。这个门洞的面积是多少平方米?
23.下图中圆的周长是62.8厘米,圆的面积正好与长方形的面积相等,你能求出图中阴影部分的面积吗?
24.如图,把4个半径为5厘米的圆柱形塑料管用绳子捆扎在一起。
(1)一根塑料管的横截面(如图中阴影部分)面积是多少?
(2)图中的线段的长度相当于圆的( ),曲线b的长度是( )厘米。打结部分绳长25厘米,那么捆扎这4个塑料管需用多少厘米的绳子?
参考答案:
1.B
【分析】假设小圆的半径是1,则小圆的直径:1×2=2,则大圆的半径是2,根据圆的面积公式:π×半径2,分别求出大圆和小圆的面积,用大圆面积除以小圆面积即可。
【详解】假设小圆的半径是1,则大圆的半径:1×2=2
小圆面积:π×1×1=π
大圆面积:2×2×π=4π
4π÷π=4
故答案选:B
【点睛】本题主要考查圆的面积公式,熟练掌握圆的面积公式并灵活运用。
2.D
【分析】如图所示,设大圆半径为R,小圆的半径为r,则图中大正方形边长为R,小正方形的边长为r,则阴影部分的面积=R2-r2,根据圆环面积=π(R2-r2),据此解答即可。
【详解】设大圆半径为R,小圆半径为r。
则阴影部分的面积=R2-r2=9平方厘米。
3.14×(R2-r2)
=3.14×9
=28.26(平方厘米)
即圆环面积是28.26平方厘米。
故答案为:D
【点睛】解答此题的关键:用大圆和小圆的半径表示出阴影部分的面积,进而求出圆环面积。
3.A
【分析】根据圆环面积=外圆面积-内圆面积,即可解答。
【详解】圆环面积=πR -πr =π(R -r )。
故答案为:A
【点睛】本题考查圆环的面积,根据公式解答。
4.C
【分析】根据题意可知,甲图的阴影部分的面积是边长为10的正方形面积减去4个半径是(10÷4)圆的面积;乙图是一个边长是10的正方形面积减去半径为(10÷2)的圆的面积;根据正方形面积公式:边长×边长;圆的面积公式:π×半径2,代入数据,求出阴影部分的面积,再进行比较,即可解答。
【详解】甲图阴影部分面积:
10×10-3.14×(10÷4)2×4
=100-3.14×6.25×4
=100-19.625×4
=100-78.5
=21.5
乙图阴影部分面积:
10×10-3.14×(10÷2)2
=100-3.14×25
=100-78.5
=21.5
21.5=21.5
甲图阴影部分面积和乙图阴影部分面积一样大。
故答案选:C
【点睛】本题考查正方形面积公式、圆的面积公式的应用,关键是熟记公式。
5.B
【分析】观察图形可知,阴影部分半圆的半径是空白半圆半径的一半,设阴影部分半圆的半径为1,则空白半圆的半径为1×2=2,根据圆的面积公式:π×半径2,求出阴影部分半圆的面积和空白半圆的面积,再用阴影部分面积除以空白半圆面积,即可解答。
【详解】设阴影部分半圆的半径为1,则空白半圆半径为:1×2=2
阴影部分半圆面积:π×12×=π
空白半圆面积:π×(1×2)2×
=π×4×
=2π
π÷2π=×=
阴影部分的面积是空白部分面积的。
故答案选:B
【点睛】本题考查圆的面积公式的应用,关键是熟记公式,以及求一个数占另一个数的几分之几。
6.B
【分析】
观察图可知,正方形的面积等于两个等腰直角三角形面积组成,三角形的斜边是圆的直径,斜边对应的高是圆的半径,根据三角形的面积=底×高÷2,半径表示为r,一个等腰直角三角形的面积可表示为2r×r÷2,也就是r2,2个等腰直角三角形的面积则表示为2r2;根据圆面积公式:S=πr2,用π÷π即可求出r2是多少,再乘2即可求出正方形的面积。
【详解】如图:
要使正方形的面积最大,正方形的对角线为圆的直径,
设圆的半径为r,圆的面积为πr2,正方形的面积为:2r2
π×r2=π
解:r2=π÷π
r2=1
所以正方形的面积为:2×1=2(平方米)
正方形的面积是2平方米。
故答案为:B
【点睛】本题主要考查了正方形和圆的关系,熟记相关公式是解答本题的关键。
7. 8 4 12.56
【分析】根据题意可知,长方形喷绘布的长是圆的直径的2倍,宽是圆的直径,根据圆的面积S=πr2求出圆的面积。
【详解】长方形喷绘布的长至少是4×2=8米,宽至少是4米。
每个鼓面的面积:
3.14×(4÷2)2
= 3.14×4
=12.56(平方米)
【点睛】重点考查了圆的面积的实际应用,计算时要认真。
8. 4.71 7.065cm2 113.04 339.12cm2
【分析】经过三小时,时针针尖走了3÷12=圆的周长,时针扫过的面积是圆的面积。又因时针长3厘米,即时针所经过的圆的半径是3厘米,从而利用圆的周长、面积公式解答即可;经过三小时,分针转了三圈,又因分针长6厘米,即分针所经过的圆的半径是6厘米,从而利用圆的周长、面积公式求解即可。
【详解】3.14×3×2×(3÷12)
=18.84×
=4.71(厘米)
3.14×32×
=28.26×
=7.065(平方厘米)
3.14×6×2×3
=3.14×36
=113.04(厘米)
3.14×62×3
=3.14×36×3
=113.04×3
=339.12(平方厘米)
【点睛】本题主要考查圆的周长、面积公式的实际应用,解题时要明确经过三小时,时针旋转圆,分针旋转3圈。
9.50.24
【分析】根据题意,长方形内画最大的圆,圆的直径等于长方形的宽;根据圆的面积公式:π×半径2,代入数据,即可解答。
【详解】3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24(cm2)
【点睛】本题考查圆的面积公式的应用;关键明确长方形内画最大的圆,圆的直径等于长方形的宽。
10. 150.72 28.26
【分析】从中午12时到下午3时,分针旋转了3圈,时针旋转了3大格,旋转一大格是30°,由此可知时针旋转了3×30°=90°,根据圆的周长C=πd,圆的面积S=πr2,解答即可。
【详解】3.14×(2×8)×3
=3.14×16×3
=50.24×3
=150.72(厘米)
分针针尖走过了150.72厘米。
3.14×62×
=113.04×
=28.26(平方厘米)
时针扫过的面积是28.26平方厘米。
【点睛】此题考查了圆的周长和面积的相关计算,掌握公式并能灵活运用是解题关键。
11. 45°
【分析】根据题意,一张圆片对折3次,就是把这根圆片平均分成8份,求一份占圆片的几分之几,把圆片的面积看作单位“1”,用1÷8,即可;圆心角是360°,再用圆心角360°×一个扇形占圆片面积的分率,即可解答。
【详解】1÷8=
360°×=45°
【点睛】利用分数的意义以及求一个数的几分之几是多少。
12.3.14
【分析】蚂蚁走过的路程刚好是圆周长的一半,圆的周长=2πr,则周长的一半=πr,代入不同的半径,求出两个路程的长度作差即可。
【详解】大半径:10+1=11(厘米)
3.14×11-3.14×10
=34.54-31.4
=3.14(厘米)
它们爬过的路程相差3.14厘米。
【点睛】此题主要考查圆的周长公式,熟练掌握它的公式并灵活运用。
13.×
【分析】圆的周长=2π×半径,如果大圆的周长是小圆周长的4倍,则大圆的半径就是小圆半径的4倍。设小圆半径为r,则大圆半径为4r,根据圆的面积公式:π×半径2,即可解答。
【详解】大圆周长是小圆周长的4倍,则大圆半径是小圆半径的4倍。
设:小圆半径为r,则大圆半径为4r。
小圆面积为:πr2
大圆面积为:π×(4r)2=16πr2
πr2÷16πr2=
大圆周长是小圆周长的4倍,那么小圆面积是大圆面积的。
故答案为:×
【点睛】本题考查圆的周长公式、面积公式的应用,关键是熟记公式,灵活运用。
14.×
【分析】任意一个圆的周长与它的直径的比值都是一个固定的数,我们把它叫做圆周率,据此解答即可。
【详解】根据圆周率的含义可知:大小两个圆,它们的圆周率都相等,故本题说法错误。
【点睛】此题考查对圆周率的认识,圆周率是一个固定不变的数。
15.×
【分析】半径决定圆的大小,画圆时,圆规两脚之间的距离等于所画圆的半径。根据题意,圆的周长单位是厘米,面积单位是平方厘米,长度单位和面积单位是无法比较大小的,据此判断即可。
【详解】由题意可知:圆规两脚之间的距离是2厘米,即半径是2厘米,所画的圆周长单位是厘米,面积单位是平方厘米,周长和面积不能比较大小。原题说法错误。
故答案为:×
【点睛】解答此题的关键是确定:长度单位和面积单位是无法比较大小的。
16.×
【分析】半圆的周长=圆周长的一半+直径,据此判断。
【详解】如果一个圆的周长是2πr厘米,那么半圆的周长是2πr÷2+2r=πr+2r厘米。原题说法错误。
故答案为:×
【点睛】此题考查了圆周长的相关知识,注意半圆的周长记得加一个直径的长度。
17.×
【分析】圆的周长=2πr,圆的面积=πr2 ,圆的半径变为原来的,圆的周长也变为原来的,圆的面积则会缩小到原来的的平方。由此即可解答。
【详解】一个圆的半径缩小到原来的,它的周长也缩小到原来的,面积缩小到原来的
故答案为:×。
【点睛】此题考查了圆的半径与周长、面积的关系,理解掌握公式是解答的关键。
18.48;34.74
【分析】第一个图形将扇形通过顺时针旋转,可得阴影部分的面积相当于一个长方形的面积,长是8,宽是6,根据长方形的面积=长×宽,代入数据解答。
第二个图形的阴影面积=梯形的面积-扇形的面积,梯形的上底是6、下底是15、高是6,根据梯形的面积=(上底+下底)×高÷2,代入数据即可求出梯形的面积,扇形的面积相当于半径是6的圆面积的,根据圆面积公式:S=πr2以及分数乘法的意义,用3.14×62×即可求出扇形的面积,进而用减法求出阴影部分的面积。
【详解】8×6=48
第一个阴影部分的面积是48;
(6+15)×6÷2
=21×6÷2
=63
3.14×62×
=3.14×36×
=28.26
63-28.26=34.74
阴影部分的面积是34.74。
19.1130.4米
【分析】车轮转一圈的长度就是车轮的周长,根据圆的周长=πd求出车轮转一圈的长度,再乘每分钟转的圈数求出车轮1分钟前进的速度,最后乘时间5分钟即可求出路程。
【详解】0.6×3.14×120×5
=1.884×120×5
=226.08×5
=1130.4(米)
答:5分钟可以行1130.4米。
【点睛】本题考查圆的周长的应用,要理解车轮转一圈的长度就是车轮的周长。
20.0.41平方米
【分析】桌面可以收起来的部分的面积=圆的面积-正方形的面积;圆的面积=πr2,圆的直径刚好是正方形的对角线,正方形的面积=对角线×对角线÷2,直接代入数据计算即可。
【详解】圆的面积:
3.14×(1.2÷2)2
=3.14×0.62
=3.14×0.36
=1.1306(平方米)
正方形的面积:
1.2×1.2÷2
=1.44÷2
=0.72(平方米)
收起来的面积:
1.1306-0.72=0.4106≈0.41(平方米)
答:桌面可以收起来的部分的面积是0.41平方米。
【点睛】此题主要考查圆的面积公式,掌握正方形面积的求法也是解题的关键。
21.25.12平方米
【分析】观察题意可知,篱笆的长度相当于圆周长的一半,根据圆周长公式:C=2πr,用2×12.56÷2÷3.14即可求出半径,也就是4米,再根据圆面积公式:S=πr2,用3.14×42÷2即可求出半圆的面积。
【详解】2×12.56÷2÷3.14=4(米)
3.14×42÷2
=3.14×16÷2
=25.12(平方米)
答:这个半圆形兔舍的面积是25.12平方米。
【点睛】本题考查了圆周长公式、圆面积公式的灵活应用,要熟练掌握相关公式。。
22.10.28平方米
【分析】由图可知,门洞的面积=直径是2米的圆的面积×2+边长是2米的正方形的面积;根据圆的半径:r=d÷2,圆的面积:S=π,正方形的面积:S=a×a;据此代入数据解答。
【详解】由分析得:
=3.14×1×2+4
=6.28+4
=10.28(平方米)
答:这个门洞的面积是10.28平方米。
【点睛】此题主要考查组合图形的面积,关键是把不规则图形转化成规则图形,利用规则图形的面积公式计算。
23.235.5平方厘米
【分析】通过分析图形可知,阴影部分的面积=长方形面积-圆面积,因此先利用圆的周长公式:求出圆的半径,然后通过圆的面积公式:求出圆的面积,已知圆的面积=长方形面积,由此即可解答。
【详解】圆的半径:62.8÷3.14÷2
=20÷2
=10(厘米)
长方形面积=圆的面积=3.14×10=314(平方厘米)
314-314÷4
=314-78.5
=235.5(平方厘米)
答:阴影部分的面积是235.5平方厘米。
【点睛】此题主要考查了学生对圆的周长和面积公式的理解与灵活应用解题能力。
24.(1)78.5平方厘米;(2)直径;7.85;96.4厘米
【分析】(1)一根塑料管的横截面面积是半径为5cm的圆的面积,然后再根据圆的面积公式S=πr2进行解答。
(2)图中的线段的长度相当于圆的直径,曲线b的长度相当于半径为5cm的圆的周长;捆扎这4个塑料管的绳子长度=半径为5cm的圆的周长+圆的直径×4+打结部分绳长;然后再根据圆的周长公式C=2πr,d=2r进行解答。
【详解】(1)3.14×52
=3.14×25
=78.5(平方厘米)
答:一根塑料管的横截面(如图中阴影部分)面积是78.5平方厘米。
(2)2×3.14×5×
=6.28×5×
=31.4×
=7.85(厘米)
即图中的线段的长度相当于圆的直径,曲线b的长度是7.85厘米。
2×3.14×5+2×5×4+25
=6.28×5+10×4+25
=31.4+40+25
=71.4+25
=96.4(厘米)
答:那么捆扎这4个塑料管需用96.4厘米的绳子。
【点睛】考查了圆的面积公式和周长公式的运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
