苏教版五年级上册第二单元多边形的面积综合测试卷(含答案)
文档属性
| 名称 | 苏教版五年级上册第二单元多边形的面积综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 14:14:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
苏教版五年级上册第二单元多边形的面积综合测试卷(含答案)
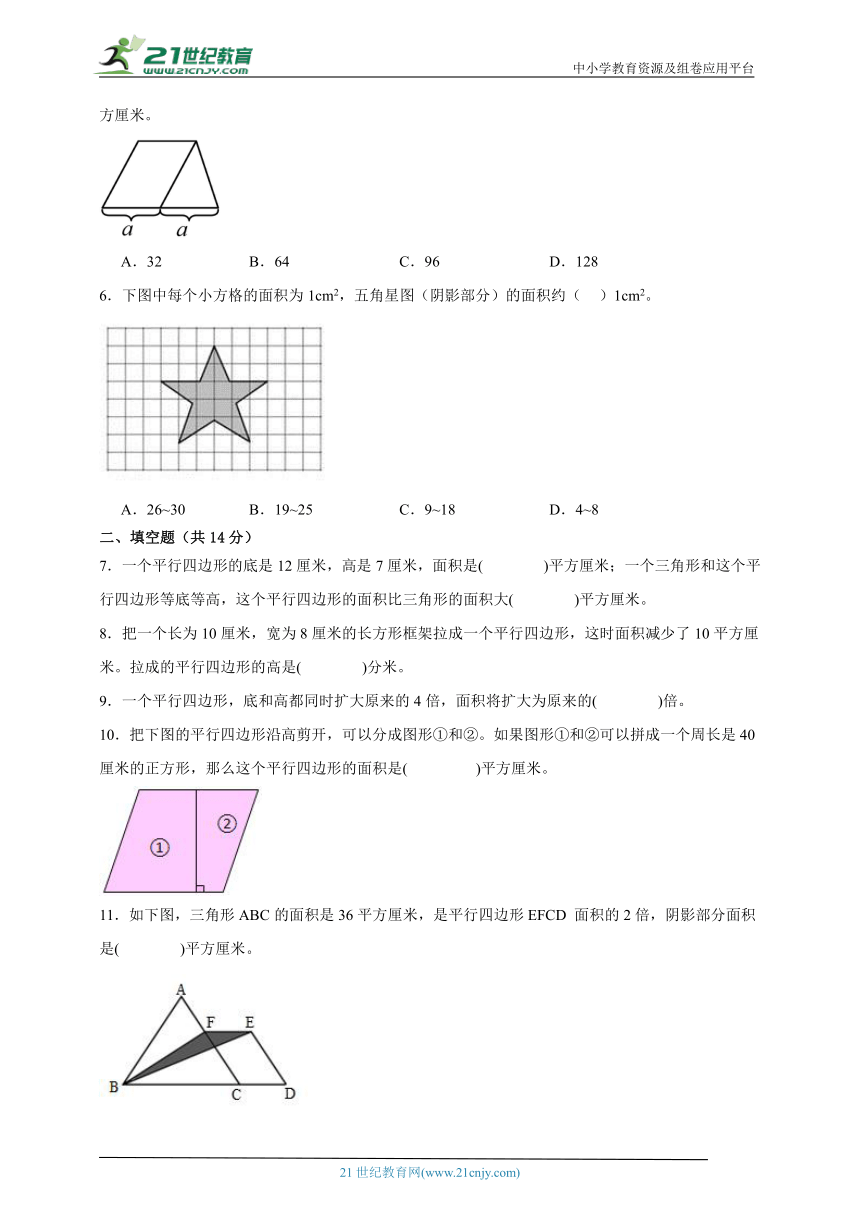
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共18分)
1.如图,三个图形A、B、C的面积,按从小到大排列是( )。
A. B.
C. D.
2.一个平行四边形与一个三角形面积相等,底也相等。如果平行四边形的高是6厘米,那么三角形的高是( )厘米。
A.3 B.6 C.9 D.12
3.下图中,点是正方形的边上的三等分点,那么三角形的面积是( )平方厘米。
A.3 B.6 C.9 D.18
4.一个三角形和一个平行四边形的面积相等,底也相等,如果三角形的高是6厘米,那么平行四边形的高是( )厘米。
A.24 B.12 C.6 D.3
5.如图,梯形被分为平行四边形和三角形,三角形的面积是32平方厘米,梯形的面积是( )平方厘米。
A.32 B.64 C.96 D.128
6.下图中每个小方格的面积为1cm2,五角星图(阴影部分)的面积约( )1cm2。
A.26~30 B.19~25 C.9~18 D.4~8
二、填空题(共14分)
7.一个平行四边形的底是12厘米,高是7厘米,面积是( )平方厘米;一个三角形和这个平行四边形等底等高,这个平行四边形的面积比三角形的面积大( )平方厘米。
8.把一个长为10厘米,宽为8厘米的长方形框架拉成一个平行四边形,这时面积减少了10平方厘米。拉成的平行四边形的高是( )分米。
9.一个平行四边形,底和高都同时扩大原来的4倍,面积将扩大为原来的( )倍。
10.把下图的平行四边形沿高剪开,可以分成图形①和②。如果图形①和②可以拼成一个周长是40厘米的正方形,那么这个平行四边形的面积是( )平方厘米。
11.如下图,三角形ABC的面积是36平方厘米,是平行四边形EFCD 面积的2倍,阴影部分面积是( )平方厘米。
12.一个梯形的上底和下底的平均长度是50厘米,高是3厘米,面积是( )平方厘米。
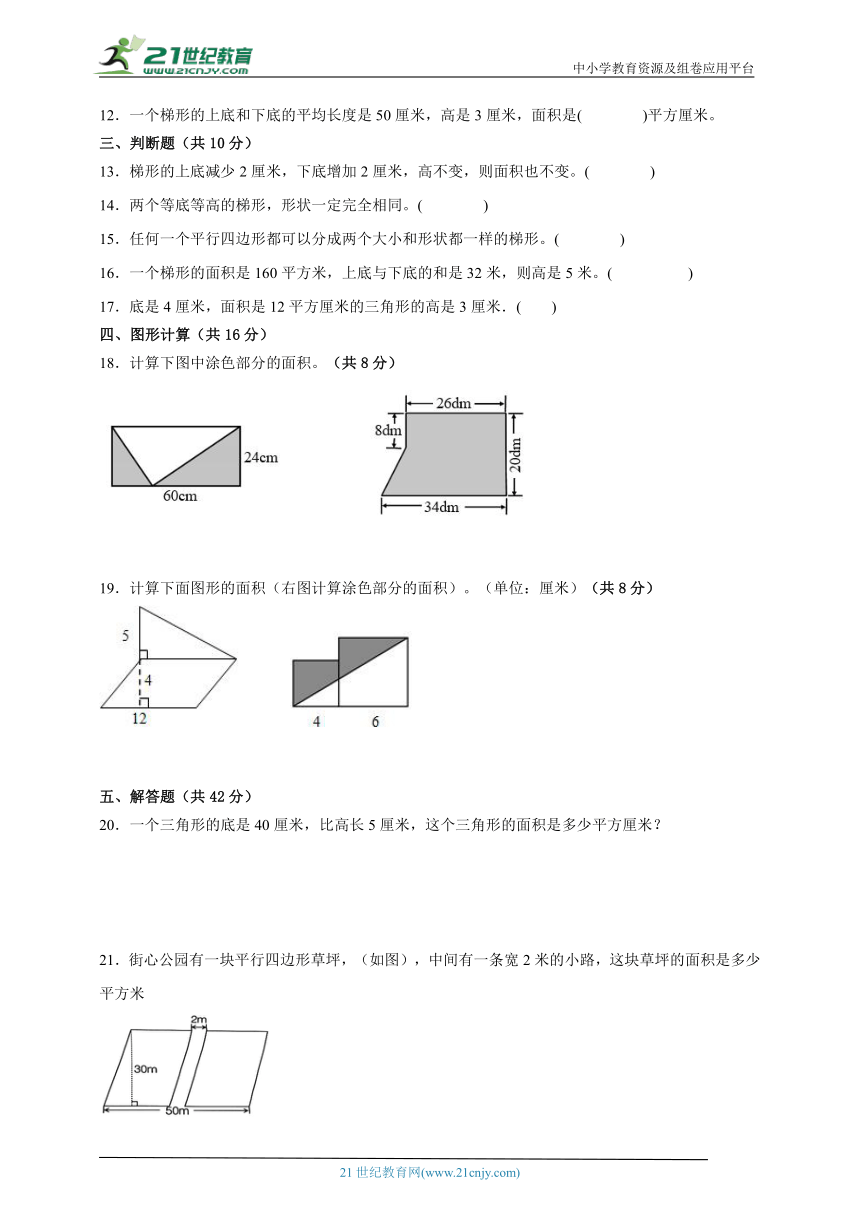
三、判断题(共10分)
13.梯形的上底减少2厘米,下底增加2厘米,高不变,则面积也不变。( )
14.两个等底等高的梯形,形状一定完全相同。( )
15.任何一个平行四边形都可以分成两个大小和形状都一样的梯形。( )
16.一个梯形的面积是160平方米,上底与下底的和是32米,则高是5米。( )
17.底是4厘米,面积是12平方厘米的三角形的高是3厘米.( )
四、图形计算(共16分)
18.计算下图中涂色部分的面积。(共8分)
19.计算下面图形的面积(右图计算涂色部分的面积)。(单位:厘米)(共8分)
五、解答题(共42分)
20.一个三角形的底是40厘米,比高长5厘米,这个三角形的面积是多少平方厘米?
21.街心公园有一块平行四边形草坪,(如图),中间有一条宽2米的小路,这块草坪的面积是多少平方米
22.如图,刘奶奶把一块梯形菜地分成两部分,分别用来种土豆和茄子,已知种茄子的面积是180平方米,那么种土豆的面积是多少平方米?
23.如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度.
24.把一张长方形纸折叠成一个梯形,如图所示。(单位:厘米)
(1)原来长方形的长是多少厘米?
(2)现在梯形面积是多少平方厘米?
25.
(1)图中阴影部分图形的面积是( )平方厘米。
(2)在图中分别画一个与阴影部分图形面积相等的平行四边形和三角形。
参考答案:
1.C
【分析】设三个图形A、B、C的高都是h,根据梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,平行四边形的面积=底×高,代入计算进而比较面积的大小。
【详解】设三个图形A、B、C的高都是h。
图形A:(4+6)h÷2=5h;
图形B:11h÷2=5.5h;
图形C:6h;
所以按照从小到大排列是。
故选择:C
【点睛】此题考查了多边形的面积计算,需掌握其计算公式并能灵活运用。
2.D
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2。面积和底相等的三角形和平行四边形,三角形的高是平行四边形高的2倍。据此计算。
【详解】6×2=12(厘米)
故答案为:D
【点睛】灵活运用平行四边形和三角形的面积公式是解题的关键。
3.B
【解析】略
4.D
【分析】三角形的面积=底×高÷2,平行四边形的面积=底×高;若面积相等,底也相等,则三角形的高是平行四边形高的2倍;据此解答。
【详解】面积相等,底也相等,则三角形的高是平行四边形高的2倍,所以平行四边形的高为:6÷2=3(厘米)
故答案为:D
【点睛】本题主要考查三角形、平行四边形面积公式的灵活运用。
5.C
【分析】根据图可知,三角形的底和平行四边形的底是相同的,高也是相同的,根据平行四边形的面积公式:底×高;三角形的面积公式:底×高÷2,由此即可知道等底等高的平行四边形的面积是三角形面积的2倍,则平行四边形的面积是:32×2=64(平方厘米),再加上三角形的面积即可求出梯形的面积。
【详解】32×2+32
=64+32
=96(平方厘米)
所以梯形的面积是96平方厘米。
故答案为:C
【点睛】本题主要考查平行四边形和三角形的面积公式,熟练掌握它们的面积公式并灵活运用。
6.C
【分析】首先把图形用方格划分,注意每一部分估算取整(其中不足1格的按照半格计算),最后合并即可得出答案。
【详解】有4个整格子,16个半方格,大约有12个方格,因为每个小方格的面积是1cm2,因此面积为12cm2。
故答案为:C
【点睛】解决此题的关键是利用割补法,把不规则的图形拼为规则的图形,进一步估算面积即可。
7. 84 42
【分析】根据平行四边形的面积公式:S=ah,据此求出它的面积;一个三角形和这个平行四边形等底等高,则三角形的面积是平行四边形的面积的一半,然后用平行四边形的面积减去三角形的面积。
【详解】12×7=84(平方厘米)
84÷2=42(平方厘米)
84-42=42(平方厘米)
则一个平行四边形的底是12厘米,高是7厘米,面积是84平方厘米;一个三角形和这个平行四边形等底等高,这个平行四边形的面积比三角形的面积大42平方厘米。
【点睛】本题考查三角形和平行四边形的面积,熟记公式是解题的关键。
8.0.7或0.875
【分析】根据长方形面积计算公式,求出这个长方形的面积,减去10平方厘米,也就是拉成的平行四边形的面积,根据平行四边形面积计算公式可知,平行四边形的高等于面积除以底,据此解题即可,注意平行四边形的每条边都可以看作它的底。
【详解】10×8=80(平方厘米)
(80-10)÷10
=70÷10
=7(厘米)
(80-10)÷8
=70÷8
=8.75(厘米)
7厘米=0.7分米
8.75厘米=0.875分米
所以,拉成的平行四边形的高是0.7分米或0.875分米。
【点睛】本题的关键根据对应的底不同分情况讨论高,注意单位换算。
9.16
【分析】根据平行四边形的面积S=ah,底和高同时扩大到原来的4倍后,表示出底和高扩大后平行四边形的面积,再除以原来平行四边形的面积即可。
【详解】由分析可知,扩大后的面积为4a×4h=16 ah,16ah÷ah=16,面积将扩大为原来的16倍。
【点睛】此题主要考查平行四边形面积的变化规律,明确面积扩大的倍数是底和高扩大倍数的积。
10.100
【解析】略
11.9
【分析】根据题意可知,三角形ABC的面积是平行四边形EFCD面积的2倍,用三角形ABC的面积÷2,求出平行四边形EFCD的面积;阴影部分是三角形,与平行四边形EFCD是等底等高,所以阴影部分面积是平行四边形EFCD面积的一半,据此解答。
【详解】36÷2÷2
=18÷2
=9(平方厘米)
如下图,三角形ABC的面积是36平方厘米,是平行四边形EFCD 面积的2倍,阴影部分面积是9平方厘米。
【点睛】解答本题的关键明确阴影部分面积与平行四边形EFCD面积之间的关系。
12.150
【分析】根据平均数的意义可知,(上底+下底)÷2为50厘米,再根据梯形的面积=(上底+下底)×高÷2,用50×3即可求出梯形的面积。
【详解】50×3=150(平方厘米)
一个梯形的上底和下底的平均长度是50厘米,高是3厘米,面积是150平方厘米。
【点睛】本题主要考查了梯形面积公式的灵活应用,要熟练掌握相关公式。
13.√
【分析】梯形面积=(上底+下底)×高÷2,结合面积公式进行判断即可。也可以举例用实际数据计算来加以判断。
【详解】上底和下底都变化了,但上底与下底的和没有变,高也没有变,面积也就不变。
故答案为:√
【点睛】本题考查梯形面积公式的掌握情况,结合公式就能做出正确判断。
14.×
【详解】两个等底等高的梯形是底和高完全相等,但由于底的位置不同,会导致对角线的长度不一样,因此其形状不一定完全相同。但是它们的面积是相等的。原题说法错误。
故答案为:×。
15.√
【分析】根据平行四边形的两组对边分别平行且相等的特性,梯形只有一组对边平行的特征,可解答此题。
【详解】根据以上分析,画图如下:
所以一个平行四边形用一条线段可以将它分成两个完全一样的梯形,此说法是正确的。
故答案为:√。
【点睛】清楚掌握平行四边形和梯形的特征是解决本题的关键。
16.×
【分析】由题可知,梯形的面积是160平方米,上底与下底的和是32米。由梯形面积=(上底+下底)×高÷2。据此可解。
【详解】160×2÷32
=320÷32
=10(米)
即梯形的高为10米。
故答案为:×。
【点睛】此题考查的是梯形的面积公式,能熟练掌握并应用是解题的关键。
17.×
【解析】略
18.720cm2;568dm2
【分析】根据对上左图的观察,其涂色部分面积等于一个长方形面积减去一个白色三角形面积,根据长方形面积公式:长方形面积=长×高,三角形面积=底×高÷2,代入数据求解即可;
根据对上右图的观察,这个组合图形由上半部分的一个长方形,和下半部分的一个梯形组成,根据长方形面积公式:长方形面积=长×高,梯形面积=(上底+下底)×高÷2,代入数据求解即可。
【详解】上左图涂色面积:
60×24-60×24÷2
=1440-1440÷2
=1440-720
=720(cm2)
上右图涂色面积:
8×26+(26+34)×(20-8)÷2
=208+60×12÷2
=208+720÷2
=208+360
=568(dm2)
19.78平方厘米;22平方厘米
【分析】第一个图形的面积=底是12厘米,高是4厘米的平行四边形面积+底是12厘米,高是5厘米的三角形面积;根据平行四边形面积公式:底×高;三角形面积公式:底×高÷2,代入数据,即可解答;
第二个图形阴影部分面积=边长是4厘米正方形面积+边长是6厘米的正方形面积-底是6厘米,高是(4+6)厘米的三角形面积;根据正方形面积公式:边长×边长;三角形面积公司:底×高÷2,代入数据,即可解答。
【详解】12×4+12×5÷2
=48+60÷2
=48+30
=78(平方厘米)
4×4+6×6-6×(6+4)÷2
=16+36-6×10÷2
=52-60÷2
=52-30
=22(平方厘米)
20.35厘米 700平方厘米
【详解】40-5=35(厘米)
40×35÷2=700(平方厘米)
21.1440平方米
【分析】草坪的面积等于底是50米,高是30米的平行四边形面积减去底是2米,高是30米的平行四边形面积;根据平行四边形面积公式:面积=底×高,代入数据,即可解答。
【详解】50×30-2×30
=1500-60
=1440(平方米)
答:这块草坪的面积是1440平方米。
【点睛】明确小路的面积是平行四边形的面积是解答本题的关键。
22.60平方米
【分析】根据平行四边形的面积公式,用种茄子的面积÷平行四边形的边长,求出平行四边形的高(梯形的高),再将三角形的底和高带入三角形的面积公式即可。
【详解】180÷12×8÷2
=15×8÷2
=120÷2
=60(平方米)
答:种土豆的面积是60平方米。
【点睛】本题考查平行四边形、三角形面积公式的应用,求出梯形的高是解题的关键。
23.36.5厘米
【详解】试题分析:由“阴影部分的面积比三角形EFH的面积大120cm2”可知:平行四边形的面积比三角形ABE的面积大120平方厘米,利用平行四边形和三角形的面积公式即可求解.
解:80×HB﹣80×70÷2=120,
80HB﹣2800=120,
80HB=2920,
HB=36.5,
答:HB的长度是36.5厘米.
点评:解答此题的关键是明白:平行四边形的面积比三角形ABE的面积大120平方厘米.
24.(1)21厘米
(2)120平方厘米
【分析】(1)通过观察图形可知,原来长方形的长是(6+9+6)厘米,据此解答。
(2)图形的上底是9厘米,下底等于长方形的长,高等于长方形的宽,根据梯形的面积公式:S=(a+b)×h÷2,把数据代入公式解答。
【详解】(1)6+9+6=21(厘米)
答:原来长方形的长是21厘米。
(2)(9+21)×8÷2
=30×8÷2
=240÷2
=120(平方厘米)
答:现在梯形的面积是120平方厘米。
【点睛】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
25.(1)16
(2)见详解
【分析】(1)由图意可知,图中阴影部分图形是一个梯形,上底是2cm,下底是6cm,高是4cm,梯形的面积=(上底+下底)×高÷2;据此解答;
(2)根据梯形面积16平方厘米、平行四边形的面积计算公式“S=ah”,只要所画的平行四边形的底和高的积等于16即可;根据三角形的面积公式“S=ah”,只要画出的三角形底为所画平行四边形的2倍,高相等或高为所画平行四边形的2倍,底相等,面积就是相等。
【详解】(1)(2+6)×4÷2
=8×4÷2
=16(平方厘米)
(2)根据分析画图如下:
【点睛】此题考查的是梯形的面积以及根据面积画平行四形、三角形,所画图形答案不唯一,只要面积符合题意即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
苏教版五年级上册第二单元多边形的面积综合测试卷(含答案)
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共18分)
1.如图,三个图形A、B、C的面积,按从小到大排列是( )。
A. B.
C. D.
2.一个平行四边形与一个三角形面积相等,底也相等。如果平行四边形的高是6厘米,那么三角形的高是( )厘米。
A.3 B.6 C.9 D.12
3.下图中,点是正方形的边上的三等分点,那么三角形的面积是( )平方厘米。
A.3 B.6 C.9 D.18
4.一个三角形和一个平行四边形的面积相等,底也相等,如果三角形的高是6厘米,那么平行四边形的高是( )厘米。
A.24 B.12 C.6 D.3
5.如图,梯形被分为平行四边形和三角形,三角形的面积是32平方厘米,梯形的面积是( )平方厘米。
A.32 B.64 C.96 D.128
6.下图中每个小方格的面积为1cm2,五角星图(阴影部分)的面积约( )1cm2。
A.26~30 B.19~25 C.9~18 D.4~8
二、填空题(共14分)
7.一个平行四边形的底是12厘米,高是7厘米,面积是( )平方厘米;一个三角形和这个平行四边形等底等高,这个平行四边形的面积比三角形的面积大( )平方厘米。
8.把一个长为10厘米,宽为8厘米的长方形框架拉成一个平行四边形,这时面积减少了10平方厘米。拉成的平行四边形的高是( )分米。
9.一个平行四边形,底和高都同时扩大原来的4倍,面积将扩大为原来的( )倍。
10.把下图的平行四边形沿高剪开,可以分成图形①和②。如果图形①和②可以拼成一个周长是40厘米的正方形,那么这个平行四边形的面积是( )平方厘米。
11.如下图,三角形ABC的面积是36平方厘米,是平行四边形EFCD 面积的2倍,阴影部分面积是( )平方厘米。
12.一个梯形的上底和下底的平均长度是50厘米,高是3厘米,面积是( )平方厘米。
三、判断题(共10分)
13.梯形的上底减少2厘米,下底增加2厘米,高不变,则面积也不变。( )
14.两个等底等高的梯形,形状一定完全相同。( )
15.任何一个平行四边形都可以分成两个大小和形状都一样的梯形。( )
16.一个梯形的面积是160平方米,上底与下底的和是32米,则高是5米。( )
17.底是4厘米,面积是12平方厘米的三角形的高是3厘米.( )
四、图形计算(共16分)
18.计算下图中涂色部分的面积。(共8分)
19.计算下面图形的面积(右图计算涂色部分的面积)。(单位:厘米)(共8分)
五、解答题(共42分)
20.一个三角形的底是40厘米,比高长5厘米,这个三角形的面积是多少平方厘米?
21.街心公园有一块平行四边形草坪,(如图),中间有一条宽2米的小路,这块草坪的面积是多少平方米
22.如图,刘奶奶把一块梯形菜地分成两部分,分别用来种土豆和茄子,已知种茄子的面积是180平方米,那么种土豆的面积是多少平方米?
23.如图,平行四边形ABCD,△EBA是直角三角形,AB=80cm,EB=70cm.已知阴影部分的面积比三角形EFH的面积大120cm2.求HB的长度.
24.把一张长方形纸折叠成一个梯形,如图所示。(单位:厘米)
(1)原来长方形的长是多少厘米?
(2)现在梯形面积是多少平方厘米?
25.
(1)图中阴影部分图形的面积是( )平方厘米。
(2)在图中分别画一个与阴影部分图形面积相等的平行四边形和三角形。
参考答案:
1.C
【分析】设三个图形A、B、C的高都是h,根据梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,平行四边形的面积=底×高,代入计算进而比较面积的大小。
【详解】设三个图形A、B、C的高都是h。
图形A:(4+6)h÷2=5h;
图形B:11h÷2=5.5h;
图形C:6h;
所以按照从小到大排列是。
故选择:C
【点睛】此题考查了多边形的面积计算,需掌握其计算公式并能灵活运用。
2.D
【分析】平行四边形的面积=底×高,三角形的面积=底×高÷2。面积和底相等的三角形和平行四边形,三角形的高是平行四边形高的2倍。据此计算。
【详解】6×2=12(厘米)
故答案为:D
【点睛】灵活运用平行四边形和三角形的面积公式是解题的关键。
3.B
【解析】略
4.D
【分析】三角形的面积=底×高÷2,平行四边形的面积=底×高;若面积相等,底也相等,则三角形的高是平行四边形高的2倍;据此解答。
【详解】面积相等,底也相等,则三角形的高是平行四边形高的2倍,所以平行四边形的高为:6÷2=3(厘米)
故答案为:D
【点睛】本题主要考查三角形、平行四边形面积公式的灵活运用。
5.C
【分析】根据图可知,三角形的底和平行四边形的底是相同的,高也是相同的,根据平行四边形的面积公式:底×高;三角形的面积公式:底×高÷2,由此即可知道等底等高的平行四边形的面积是三角形面积的2倍,则平行四边形的面积是:32×2=64(平方厘米),再加上三角形的面积即可求出梯形的面积。
【详解】32×2+32
=64+32
=96(平方厘米)
所以梯形的面积是96平方厘米。
故答案为:C
【点睛】本题主要考查平行四边形和三角形的面积公式,熟练掌握它们的面积公式并灵活运用。
6.C
【分析】首先把图形用方格划分,注意每一部分估算取整(其中不足1格的按照半格计算),最后合并即可得出答案。
【详解】有4个整格子,16个半方格,大约有12个方格,因为每个小方格的面积是1cm2,因此面积为12cm2。
故答案为:C
【点睛】解决此题的关键是利用割补法,把不规则的图形拼为规则的图形,进一步估算面积即可。
7. 84 42
【分析】根据平行四边形的面积公式:S=ah,据此求出它的面积;一个三角形和这个平行四边形等底等高,则三角形的面积是平行四边形的面积的一半,然后用平行四边形的面积减去三角形的面积。
【详解】12×7=84(平方厘米)
84÷2=42(平方厘米)
84-42=42(平方厘米)
则一个平行四边形的底是12厘米,高是7厘米,面积是84平方厘米;一个三角形和这个平行四边形等底等高,这个平行四边形的面积比三角形的面积大42平方厘米。
【点睛】本题考查三角形和平行四边形的面积,熟记公式是解题的关键。
8.0.7或0.875
【分析】根据长方形面积计算公式,求出这个长方形的面积,减去10平方厘米,也就是拉成的平行四边形的面积,根据平行四边形面积计算公式可知,平行四边形的高等于面积除以底,据此解题即可,注意平行四边形的每条边都可以看作它的底。
【详解】10×8=80(平方厘米)
(80-10)÷10
=70÷10
=7(厘米)
(80-10)÷8
=70÷8
=8.75(厘米)
7厘米=0.7分米
8.75厘米=0.875分米
所以,拉成的平行四边形的高是0.7分米或0.875分米。
【点睛】本题的关键根据对应的底不同分情况讨论高,注意单位换算。
9.16
【分析】根据平行四边形的面积S=ah,底和高同时扩大到原来的4倍后,表示出底和高扩大后平行四边形的面积,再除以原来平行四边形的面积即可。
【详解】由分析可知,扩大后的面积为4a×4h=16 ah,16ah÷ah=16,面积将扩大为原来的16倍。
【点睛】此题主要考查平行四边形面积的变化规律,明确面积扩大的倍数是底和高扩大倍数的积。
10.100
【解析】略
11.9
【分析】根据题意可知,三角形ABC的面积是平行四边形EFCD面积的2倍,用三角形ABC的面积÷2,求出平行四边形EFCD的面积;阴影部分是三角形,与平行四边形EFCD是等底等高,所以阴影部分面积是平行四边形EFCD面积的一半,据此解答。
【详解】36÷2÷2
=18÷2
=9(平方厘米)
如下图,三角形ABC的面积是36平方厘米,是平行四边形EFCD 面积的2倍,阴影部分面积是9平方厘米。
【点睛】解答本题的关键明确阴影部分面积与平行四边形EFCD面积之间的关系。
12.150
【分析】根据平均数的意义可知,(上底+下底)÷2为50厘米,再根据梯形的面积=(上底+下底)×高÷2,用50×3即可求出梯形的面积。
【详解】50×3=150(平方厘米)
一个梯形的上底和下底的平均长度是50厘米,高是3厘米,面积是150平方厘米。
【点睛】本题主要考查了梯形面积公式的灵活应用,要熟练掌握相关公式。
13.√
【分析】梯形面积=(上底+下底)×高÷2,结合面积公式进行判断即可。也可以举例用实际数据计算来加以判断。
【详解】上底和下底都变化了,但上底与下底的和没有变,高也没有变,面积也就不变。
故答案为:√
【点睛】本题考查梯形面积公式的掌握情况,结合公式就能做出正确判断。
14.×
【详解】两个等底等高的梯形是底和高完全相等,但由于底的位置不同,会导致对角线的长度不一样,因此其形状不一定完全相同。但是它们的面积是相等的。原题说法错误。
故答案为:×。
15.√
【分析】根据平行四边形的两组对边分别平行且相等的特性,梯形只有一组对边平行的特征,可解答此题。
【详解】根据以上分析,画图如下:
所以一个平行四边形用一条线段可以将它分成两个完全一样的梯形,此说法是正确的。
故答案为:√。
【点睛】清楚掌握平行四边形和梯形的特征是解决本题的关键。
16.×
【分析】由题可知,梯形的面积是160平方米,上底与下底的和是32米。由梯形面积=(上底+下底)×高÷2。据此可解。
【详解】160×2÷32
=320÷32
=10(米)
即梯形的高为10米。
故答案为:×。
【点睛】此题考查的是梯形的面积公式,能熟练掌握并应用是解题的关键。
17.×
【解析】略
18.720cm2;568dm2
【分析】根据对上左图的观察,其涂色部分面积等于一个长方形面积减去一个白色三角形面积,根据长方形面积公式:长方形面积=长×高,三角形面积=底×高÷2,代入数据求解即可;
根据对上右图的观察,这个组合图形由上半部分的一个长方形,和下半部分的一个梯形组成,根据长方形面积公式:长方形面积=长×高,梯形面积=(上底+下底)×高÷2,代入数据求解即可。
【详解】上左图涂色面积:
60×24-60×24÷2
=1440-1440÷2
=1440-720
=720(cm2)
上右图涂色面积:
8×26+(26+34)×(20-8)÷2
=208+60×12÷2
=208+720÷2
=208+360
=568(dm2)
19.78平方厘米;22平方厘米
【分析】第一个图形的面积=底是12厘米,高是4厘米的平行四边形面积+底是12厘米,高是5厘米的三角形面积;根据平行四边形面积公式:底×高;三角形面积公式:底×高÷2,代入数据,即可解答;
第二个图形阴影部分面积=边长是4厘米正方形面积+边长是6厘米的正方形面积-底是6厘米,高是(4+6)厘米的三角形面积;根据正方形面积公式:边长×边长;三角形面积公司:底×高÷2,代入数据,即可解答。
【详解】12×4+12×5÷2
=48+60÷2
=48+30
=78(平方厘米)
4×4+6×6-6×(6+4)÷2
=16+36-6×10÷2
=52-60÷2
=52-30
=22(平方厘米)
20.35厘米 700平方厘米
【详解】40-5=35(厘米)
40×35÷2=700(平方厘米)
21.1440平方米
【分析】草坪的面积等于底是50米,高是30米的平行四边形面积减去底是2米,高是30米的平行四边形面积;根据平行四边形面积公式:面积=底×高,代入数据,即可解答。
【详解】50×30-2×30
=1500-60
=1440(平方米)
答:这块草坪的面积是1440平方米。
【点睛】明确小路的面积是平行四边形的面积是解答本题的关键。
22.60平方米
【分析】根据平行四边形的面积公式,用种茄子的面积÷平行四边形的边长,求出平行四边形的高(梯形的高),再将三角形的底和高带入三角形的面积公式即可。
【详解】180÷12×8÷2
=15×8÷2
=120÷2
=60(平方米)
答:种土豆的面积是60平方米。
【点睛】本题考查平行四边形、三角形面积公式的应用,求出梯形的高是解题的关键。
23.36.5厘米
【详解】试题分析:由“阴影部分的面积比三角形EFH的面积大120cm2”可知:平行四边形的面积比三角形ABE的面积大120平方厘米,利用平行四边形和三角形的面积公式即可求解.
解:80×HB﹣80×70÷2=120,
80HB﹣2800=120,
80HB=2920,
HB=36.5,
答:HB的长度是36.5厘米.
点评:解答此题的关键是明白:平行四边形的面积比三角形ABE的面积大120平方厘米.
24.(1)21厘米
(2)120平方厘米
【分析】(1)通过观察图形可知,原来长方形的长是(6+9+6)厘米,据此解答。
(2)图形的上底是9厘米,下底等于长方形的长,高等于长方形的宽,根据梯形的面积公式:S=(a+b)×h÷2,把数据代入公式解答。
【详解】(1)6+9+6=21(厘米)
答:原来长方形的长是21厘米。
(2)(9+21)×8÷2
=30×8÷2
=240÷2
=120(平方厘米)
答:现在梯形的面积是120平方厘米。
【点睛】此题主要考查梯形面积公式的灵活运用,关键是熟记公式。
25.(1)16
(2)见详解
【分析】(1)由图意可知,图中阴影部分图形是一个梯形,上底是2cm,下底是6cm,高是4cm,梯形的面积=(上底+下底)×高÷2;据此解答;
(2)根据梯形面积16平方厘米、平行四边形的面积计算公式“S=ah”,只要所画的平行四边形的底和高的积等于16即可;根据三角形的面积公式“S=ah”,只要画出的三角形底为所画平行四边形的2倍,高相等或高为所画平行四边形的2倍,底相等,面积就是相等。
【详解】(1)(2+6)×4÷2
=8×4÷2
=16(平方厘米)
(2)根据分析画图如下:
【点睛】此题考查的是梯形的面积以及根据面积画平行四形、三角形,所画图形答案不唯一,只要面积符合题意即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
