思维拓展:数与形-数学六年级上册人教版(含答案)
文档属性
| 名称 | 思维拓展:数与形-数学六年级上册人教版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 19:55:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
思维拓展:数与形-数学六年级上册人教版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共18分)
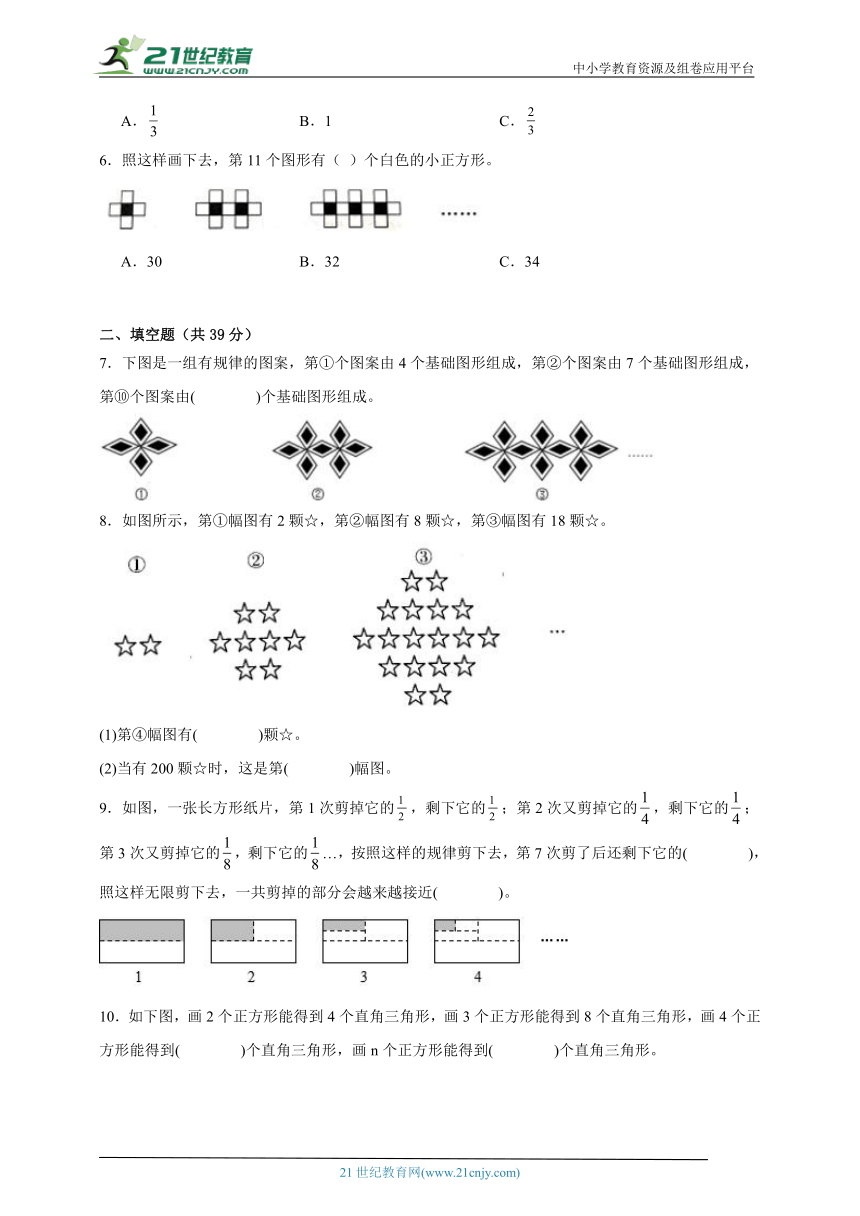
1.把同样的小棒按下面的方式摆放,第9个图形需要( )根小棒。
A.24 B.27 C.30
2.如图,连续摆n个正六边形要( )根小棒。
A.6n+1 B.6(n-1) C.5n+1
3.如图,用同样的小棒去摆,第n个图形需要小棒的根数是( )。
A.3n B.2n+1 C.3n-1
4.第四幅图形最外圈(阴影部分)有( )个“●”。
A.36 B.25 C.20
5.如下图所示,照这样的规律算下去,算式的结果是( )。
A. B.1 C.
6.照这样画下去,第11个图形有( )个白色的小正方形。
A.30 B.32 C.34
二、填空题(共39分)
7.下图是一组有规律的图案,第①个图案由4个基础图形组成,第②个图案由7个基础图形组成,第⑩个图案由( )个基础图形组成。
8.如图所示,第①幅图有2颗☆,第②幅图有8颗☆,第③幅图有18颗☆。
(1)第④幅图有( )颗☆。
(2)当有200颗☆时,这是第( )幅图。
9.如图,一张长方形纸片,第1次剪掉它的,剩下它的;第2次又剪掉它的,剩下它的;第3次又剪掉它的,剩下它的…,按照这样的规律剪下去,第7次剪了后还剩下它的( ),照这样无限剪下去,一共剪掉的部分会越来越接近( )。
10.如下图,画2个正方形能得到4个直角三角形,画3个正方形能得到8个直角三角形,画4个正方形能得到( )个直角三角形,画n个正方形能得到( )个直角三角形。
11.用火柴棒摆出图形。摆第1个图形要4根火柴棒。那么摆第15个图形要( )根火柴棒。
12.( )。
13.用同样大小的黑色五角星按如图的方式摆图案,按照这样的规律摆下去,摆第6个图案需要( )个黑色五角星,摆第10个图案需要( )个黑色五角星。
14.如图所示,如果继续画下去,第5幅图中有( )个点,第( )幅图中有127个点。
三、解答题(20-22每题6分,其余每题5分,共43分)
15.你能利用下面的图发现这一公式吗?利用你所学的面积计算的知识,探索一下.
16.数一数.
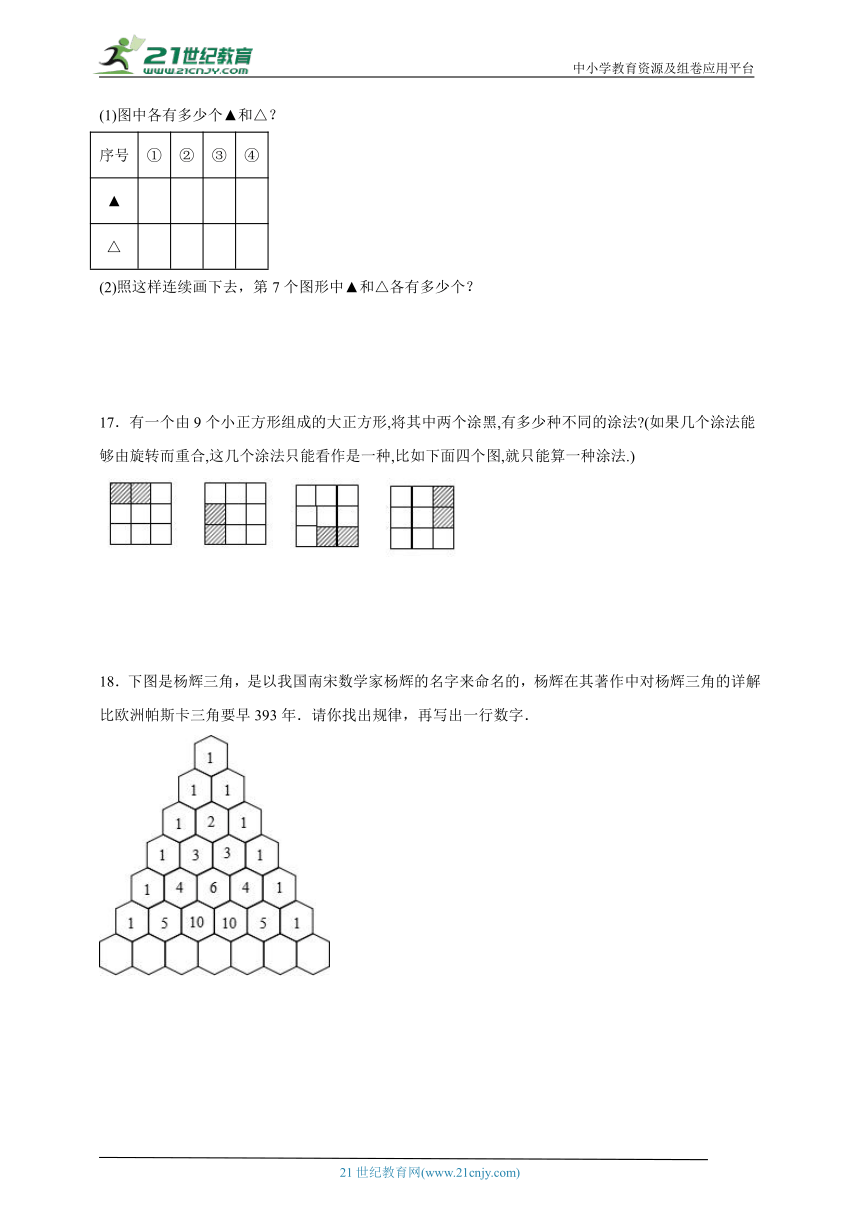
(1)图中各有多少个▲和△?
序号 ① ② ③ ④
▲
△
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
17.有一个由9个小正方形组成的大正方形,将其中两个涂黑,有多少种不同的涂法 (如果几个涂法能够由旋转而重合,这几个涂法只能看作是一种,比如下面四个图,就只能算一种涂法.)
18.下图是杨辉三角,是以我国南宋数学家杨辉的名字来命名的,杨辉在其著作中对杨辉三角的详解比欧洲帕斯卡三角要早393年.请你找出规律,再写出一行数字.
19.将一张正三角形的纸按下图形状折叠,展开后沿折痕剪开就剪出四个正三角形,我们把这称为第一次操作;再拿出其中一个正三角形,将它同样也剪成四个正三角形,我们称为第二次操作;再拿出其中一个正三角形,将它同样也剪成四个正三角形,我们称为第三次操作…
(1)根据操作的情况把下表填完整.
操作的次数 最初 第一次 第二次 第三次 第四次
共有正三角形的个数 1 4 7
(2)如果这个操作可以一直继续下去,那么第m次操作后,一共有多少个正三角形 第几次操作后,一共剪出了40个正三角形
20.在六一联欢晚会上,有一个“亲子互动”节目,用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律摆下去.
(1)摆4条“金鱼”需要多少根火柴棒?
(2)用122根火柴棒可以摆多少条“金鱼”?
21.仔细研究下面表示数的方法。
代表1 代表2 代表3 代表4
根据上面表示数的方法,
(1)下图代表( )。
(2)请在右图画圈表示18。
22.已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如上图所示)。
(1)当n = 5时,共向外作出了多少个小等边三角形?
(2)当n = k时,共向外作出了多少 个小等边三角形?(用含k的式子表示)
参考答案:
1.C
【分析】①图的小棒根数是(3+3)根,②图的小棒根数是(3+3+3)根,③图是(3+3+3+3)根,发现每一个图的小棒数都比前一个图的小棒数多3,所以第n个图需要的小棒数是(3+3n)根,代入n=9,即可求出第9个图上需要的小棒数量。
【详解】根据分析可得:第n个图需要的小棒数是(3+3n)根。
当n=9时,
即第9个图小棒数=3+3×9
=3+27
=30(根)
故答案为:C
【点睛】本题关键是找到规律,考查了学生仔细观察,善于发现的良好品质。
2.C
【分析】由图可知,摆l个正六边形需要6根小棒,摆2个正六边形需要(6+5)根小棒,摆3个正六边形需要(6+5+5)根,每增加一个正六边形就增加5根小棒,摆n个正六边形需要6+5(n-1)根小棒,据此解答。
【详解】分析可知,摆n个正六边形需要小棒的根数:
6+5(n-1)
=6+5n-5
=(5n+1)根
故答案为:C
【点睛】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键。
3.B
【分析】根据上图意可知,第一个图形用3根小棒,第二个图形用5根小棒,第三个图形用7根小棒,第四个图形用9根小棒…第n个图形需要小棒的根数是2n+1。
【详解】由分析得,
发现:每增加一个三角形就增加2根小棒,所以第n个图形需要小棒的根数是2n+1。
故选:B
【点睛】此题考查的是找规律,解答此题关键是正确找出规律并用规律解决问题。
4.C
【分析】根据题意可知,每增加一个图就增加4个“●”,据此可知,第四幅图形最外圈(阴影部分)有20个“●”。
【详解】第四幅图形最外圈(阴影部分)有20个“●”;
故答案为:C。
【点睛】根据题图找到规律是解答本题的关键。
5.C
【分析】在算式中,将提出来,将其转化为×(1++++……),再根据拆项公式=-拆项后通过加减相互抵消即可简算,然后根据分母越大分数值越小即可确定这个算式的和越接近几。
【详解】
=×(1++++……)
=×(1+1-+-+-+……)
=×2
=
故答案为:C
【点睛】解答本题的关键是提出,并灵活利用拆项公式进行简算。
6.C
【解析】略
7.31
【分析】由观察图片可见,后一个图案比前一个图案多3个基础图形;
第一个图案有基础图形的个数为:4个,
第二个图案有基础图形的个数为:
4+3×1
=4+3
=7(个)
第三个图案有基础图形的个数为:
4+3×2
=4+6
=10(个)
……
第n个图案有基础图形的个数为:
4+3(n-1)
=4+3n-3
=3n+1(个)
所以求第10个图案有几个基础图形,即n=10,代入式子即可。
【详解】由分析可得:
第n个图案有基础图形的个数为3n+1
当n=10时,式子为:
3×10+1
=30+1
=31(个)
【点睛】解决本题的关键通过观察给出的图片,找出图片之间和基础图形之间的关系,得出规律,再根据规律去解决问题。
8.(1)32
(2)⑩
【分析】第①幅图中☆的颗数表示成;第②幅图中☆的颗数表示成2+4+2=2×4=2×22;第③幅图中☆的颗数表示成2+4+6+4+2=2×9=2×32;……;由此可得。第④幅图中☆的颗数是2×42=32(颗);当有200颗☆时,200÷2=100(颗),100=10×10,故第⑩幅图中有200颗☆。
【详解】(1)2×42=32(颗)
(2)200÷2=100(颗),100=10×10
【点睛】本题主要考查学生的推理能力,关键要发现其中的规律。
9. 1
【分析】把整个图形看作单位“1”,每次剪掉部分和剩下部分相同,第1次剩下,第2次剩下,第3次剩下,第4次剩下…依次类推,第n次剪完之后还剩下它的,把n=7代入含有字母的式子求出结果;由图可知,每次剩下的部分越来越小,越来越接近0,把每次剪掉的部分相加求和,结果越来越接近1,据此解答。
【详解】分析可知,第n次剪完之后还剩下它的。
当n=7时。
=
=
=
++++…+
=1-
≈1-0
=1
所以,按照这样的规律剪下去,第7次剪了后还剩下它的,照这样无限剪下去,一共剪掉的部分会越来越接近1。
【点睛】本题主要考查应用数形结合的思想解决问题,理解一共剪掉的部分等于整体与最后一次剪掉部分的差是解答题目的关键。
10. 12 4n-4
【分析】由图可知,第1个图形有1个正方形,0个直角三角形;第2个图形有2个正方形,(4×1)个直角三角形;第3个图形有3个正方形,(4×2)个直角三角形;第4个图形有4个正方形,(4×3)个直角三角形……以此类推,每增加一个正方形就增加4个直角三角形,那么第n个图形有n个正方形,4×(n-1)个直角三角形,据此解答。
【详解】分析可知,n个正方形可以得到直角三角形的个数为:4×(n-1)
=(4n-4)个
当n=4时。
4n-4
=4×4-4
=16-4
=12(个)
所以,画4个正方形能得到12个直角三角形,画n个正方形能得到(4n-4)个直角三角形。
【点睛】找出正方形个数和直角三角形个数的变化规律是解答题目的关键。
11.46
【分析】根据火柴棒的摆设规律可知,多摆一个正方形就需要加三根火柴棒。
第1个图形需要4根火柴棒;
第2个图形需要4+3×1=4+3=7(根)火柴棒;
第3个图形需要4+3×2=4+6=10(根)火柴棒;
摆n个图形需要4+3×(n 1)(根)火柴棒;
据此,将当n=15,代入上式,计算出数量即可,据此解答。
【详解】根据火柴棒的摆设规律可知:
多摆一个正方形就需要加三根火柴棒,那么第15个图形所需要的火柴即需要:
4+3×(15-1)
=4+3×14
=4+42
=46(根)
【点睛】解答此题的关键,根据给出火柴的摆放,找到后面火柴摆放的规律。
12.0
【分析】观察算式可知,先求括号里面加法,则的值无限接近1,根据极限思想,括号里面的值等于1,据此解答即可。
【详解】
=1-1
=0
【点睛】本题考查极限思想,明确极限思想的运用是解题的关键。
13. 10 16
【分析】把图案标上序号,如下:
1 2 3 4 5 ……
图案 ……
第1行 个数 1 1 2 2 3 ……
第2行 个数 1 2 2 3 3 ……
第3行 个数 1 1 2 2 3 ……
观察图形发现:
(1)第奇数个图案的每行黑色五角星的个数是一样多的,每行有:个黑色五角星,3行则有:个黑色五角星;
(2)第偶数个图案的第一、三行的黑色五角星一样多,这两行共有n个黑色五角星,第二行共有()个,那么一共的个数是:n+=;因为第6个图案和第10个图案都是偶数,将数据代入,计算出结果即可。
【详解】根据分析,第奇数个图案黑色五角星的个数为:;第偶数个图案黑色五角星的个数为:;
当n=6时,(个);
当n=10时,(个);
【点睛】此题考查了数与形的知识,关键能够观察图案每行的数量变化找出规律再解答。
14. 25 22
【分析】第1幅图有1个点,1=6×1-5;
第2幅图有7个点,7=6×2-5;
第3幅图有13个点,13=6×3-5;
……
第n幅图有(6n-5)个点;
据此规律解答。
【详解】规律:第n幅图有(6n-5)个点。
(1)当n=5时
6n-5
=6×5-5
=30-5
=25(个)
第5幅图中有25个点;
(2)6n-5=127
解:6n-5+5=127+5
6n=132
6n÷6=132÷6
n=22
第22幅图中有127个点。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
15.从图中可以看出:
=
=
【解析】略
16.(1)1,3,6,10
3,6,10,15
(2)▲有28个,△有36个
【详解】(1)填表如下:
序号 ① ② ③ ④
▲ 1 3 6 10
△ 3 6 10 15
(2)1+2+3+4+…+7=28(个)
1+2+3+4+…+8=36(个)
答:第7个图形中▲有28个,△有36个.
17.10种
【详解】分类计算如下:当涂黑的两个方格占两角时,有2种涂法;当占两边时,也有2种涂法,当占一边一角时,有4种涂法;当占一角一中心时,有1种涂法;当占一边一中心时,也有1种涂法.
合计共有2+2+4+1+1=10(种)涂法.
18.1,6,15,20,15,6,1
【解析】略
19.(1)
操作的次数 最初 第一次 第二次 第三次 第四次
共有正三角形的个数 1 4 7 10 13
(2)13次 40个
【分析】从表格中的数据,不难发现:多剪一次,多3个正三角形.继而即可求出剪m次后正三角形的个数.
【详解】(1)由图可知没剪的时候,有一个正三角形,以后每剪一次就多出3个正三角形,所以第m次操作后,总的正三角形的个数为3m+1.第三次操作后,正三角形有:3×3+1=10(个),第四次操作后,正三角形有:3×4+1=13(个),由此可以将上表补充完整,如下:
操作的次数 最初 第一次 第二次 第三次 第四次
共有正三角形的个数 1 4 7 10 13
(2)第m次操作后,一共有3m+1个正三角形.当3m+1=40时,3m=39,m=13
答:第13次操作后,一共剪出了40个正三角形.
20.(1)26根
(2)20条
【详解】摆1条“金鱼”需要火柴棒:8根;
摆2条“金鱼”需要火柴棒:8+6=14(根);
摆3条“金鱼”需要火柴棒:8+6+6=20(根);
……
摆n条“金鱼”需要火柴棒:8+6(n﹣1)=(6n+2)根.
(1)摆4条“金鱼”需要火柴棒:
4×6+2
=24+2
=26(根)
答:摆4条“金鱼”需要26根火柴棒.
(2)6n+2=122
6n=120
n=20
答:用122根火柴棒可以摆20条“金鱼”.
21.(1)13
(2)
【分析】通过观察表示数的方法,可以看出图示是用2进制的方式表示出来的,即满2向前进1,按照从右到左的顺序,第几个格的圆就表示2的几减1次方,据此解答。
【详解】(1)由图可知,圆分别在第1、3、4格,所以这个数是20+22+23=13;图中表示的数是13。
(2)24=16,18=24+2,所以圆在第5格和第2个,画图如下:
【点睛】仔细观察图,找出其中规律是解题关键。
22.(1)9
(2)3(k-2)
【解析】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
思维拓展:数与形-数学六年级上册人教版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共18分)
1.把同样的小棒按下面的方式摆放,第9个图形需要( )根小棒。
A.24 B.27 C.30
2.如图,连续摆n个正六边形要( )根小棒。
A.6n+1 B.6(n-1) C.5n+1
3.如图,用同样的小棒去摆,第n个图形需要小棒的根数是( )。
A.3n B.2n+1 C.3n-1
4.第四幅图形最外圈(阴影部分)有( )个“●”。
A.36 B.25 C.20
5.如下图所示,照这样的规律算下去,算式的结果是( )。
A. B.1 C.
6.照这样画下去,第11个图形有( )个白色的小正方形。
A.30 B.32 C.34
二、填空题(共39分)
7.下图是一组有规律的图案,第①个图案由4个基础图形组成,第②个图案由7个基础图形组成,第⑩个图案由( )个基础图形组成。
8.如图所示,第①幅图有2颗☆,第②幅图有8颗☆,第③幅图有18颗☆。
(1)第④幅图有( )颗☆。
(2)当有200颗☆时,这是第( )幅图。
9.如图,一张长方形纸片,第1次剪掉它的,剩下它的;第2次又剪掉它的,剩下它的;第3次又剪掉它的,剩下它的…,按照这样的规律剪下去,第7次剪了后还剩下它的( ),照这样无限剪下去,一共剪掉的部分会越来越接近( )。
10.如下图,画2个正方形能得到4个直角三角形,画3个正方形能得到8个直角三角形,画4个正方形能得到( )个直角三角形,画n个正方形能得到( )个直角三角形。
11.用火柴棒摆出图形。摆第1个图形要4根火柴棒。那么摆第15个图形要( )根火柴棒。
12.( )。
13.用同样大小的黑色五角星按如图的方式摆图案,按照这样的规律摆下去,摆第6个图案需要( )个黑色五角星,摆第10个图案需要( )个黑色五角星。
14.如图所示,如果继续画下去,第5幅图中有( )个点,第( )幅图中有127个点。
三、解答题(20-22每题6分,其余每题5分,共43分)
15.你能利用下面的图发现这一公式吗?利用你所学的面积计算的知识,探索一下.
16.数一数.
(1)图中各有多少个▲和△?
序号 ① ② ③ ④
▲
△
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
17.有一个由9个小正方形组成的大正方形,将其中两个涂黑,有多少种不同的涂法 (如果几个涂法能够由旋转而重合,这几个涂法只能看作是一种,比如下面四个图,就只能算一种涂法.)
18.下图是杨辉三角,是以我国南宋数学家杨辉的名字来命名的,杨辉在其著作中对杨辉三角的详解比欧洲帕斯卡三角要早393年.请你找出规律,再写出一行数字.
19.将一张正三角形的纸按下图形状折叠,展开后沿折痕剪开就剪出四个正三角形,我们把这称为第一次操作;再拿出其中一个正三角形,将它同样也剪成四个正三角形,我们称为第二次操作;再拿出其中一个正三角形,将它同样也剪成四个正三角形,我们称为第三次操作…
(1)根据操作的情况把下表填完整.
操作的次数 最初 第一次 第二次 第三次 第四次
共有正三角形的个数 1 4 7
(2)如果这个操作可以一直继续下去,那么第m次操作后,一共有多少个正三角形 第几次操作后,一共剪出了40个正三角形
20.在六一联欢晚会上,有一个“亲子互动”节目,用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律摆下去.
(1)摆4条“金鱼”需要多少根火柴棒?
(2)用122根火柴棒可以摆多少条“金鱼”?
21.仔细研究下面表示数的方法。
代表1 代表2 代表3 代表4
根据上面表示数的方法,
(1)下图代表( )。
(2)请在右图画圈表示18。
22.已知一个面积为S的等边三角形,现将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如上图所示)。
(1)当n = 5时,共向外作出了多少个小等边三角形?
(2)当n = k时,共向外作出了多少 个小等边三角形?(用含k的式子表示)
参考答案:
1.C
【分析】①图的小棒根数是(3+3)根,②图的小棒根数是(3+3+3)根,③图是(3+3+3+3)根,发现每一个图的小棒数都比前一个图的小棒数多3,所以第n个图需要的小棒数是(3+3n)根,代入n=9,即可求出第9个图上需要的小棒数量。
【详解】根据分析可得:第n个图需要的小棒数是(3+3n)根。
当n=9时,
即第9个图小棒数=3+3×9
=3+27
=30(根)
故答案为:C
【点睛】本题关键是找到规律,考查了学生仔细观察,善于发现的良好品质。
2.C
【分析】由图可知,摆l个正六边形需要6根小棒,摆2个正六边形需要(6+5)根小棒,摆3个正六边形需要(6+5+5)根,每增加一个正六边形就增加5根小棒,摆n个正六边形需要6+5(n-1)根小棒,据此解答。
【详解】分析可知,摆n个正六边形需要小棒的根数:
6+5(n-1)
=6+5n-5
=(5n+1)根
故答案为:C
【点睛】根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键。
3.B
【分析】根据上图意可知,第一个图形用3根小棒,第二个图形用5根小棒,第三个图形用7根小棒,第四个图形用9根小棒…第n个图形需要小棒的根数是2n+1。
【详解】由分析得,
发现:每增加一个三角形就增加2根小棒,所以第n个图形需要小棒的根数是2n+1。
故选:B
【点睛】此题考查的是找规律,解答此题关键是正确找出规律并用规律解决问题。
4.C
【分析】根据题意可知,每增加一个图就增加4个“●”,据此可知,第四幅图形最外圈(阴影部分)有20个“●”。
【详解】第四幅图形最外圈(阴影部分)有20个“●”;
故答案为:C。
【点睛】根据题图找到规律是解答本题的关键。
5.C
【分析】在算式中,将提出来,将其转化为×(1++++……),再根据拆项公式=-拆项后通过加减相互抵消即可简算,然后根据分母越大分数值越小即可确定这个算式的和越接近几。
【详解】
=×(1++++……)
=×(1+1-+-+-+……)
=×2
=
故答案为:C
【点睛】解答本题的关键是提出,并灵活利用拆项公式进行简算。
6.C
【解析】略
7.31
【分析】由观察图片可见,后一个图案比前一个图案多3个基础图形;
第一个图案有基础图形的个数为:4个,
第二个图案有基础图形的个数为:
4+3×1
=4+3
=7(个)
第三个图案有基础图形的个数为:
4+3×2
=4+6
=10(个)
……
第n个图案有基础图形的个数为:
4+3(n-1)
=4+3n-3
=3n+1(个)
所以求第10个图案有几个基础图形,即n=10,代入式子即可。
【详解】由分析可得:
第n个图案有基础图形的个数为3n+1
当n=10时,式子为:
3×10+1
=30+1
=31(个)
【点睛】解决本题的关键通过观察给出的图片,找出图片之间和基础图形之间的关系,得出规律,再根据规律去解决问题。
8.(1)32
(2)⑩
【分析】第①幅图中☆的颗数表示成;第②幅图中☆的颗数表示成2+4+2=2×4=2×22;第③幅图中☆的颗数表示成2+4+6+4+2=2×9=2×32;……;由此可得。第④幅图中☆的颗数是2×42=32(颗);当有200颗☆时,200÷2=100(颗),100=10×10,故第⑩幅图中有200颗☆。
【详解】(1)2×42=32(颗)
(2)200÷2=100(颗),100=10×10
【点睛】本题主要考查学生的推理能力,关键要发现其中的规律。
9. 1
【分析】把整个图形看作单位“1”,每次剪掉部分和剩下部分相同,第1次剩下,第2次剩下,第3次剩下,第4次剩下…依次类推,第n次剪完之后还剩下它的,把n=7代入含有字母的式子求出结果;由图可知,每次剩下的部分越来越小,越来越接近0,把每次剪掉的部分相加求和,结果越来越接近1,据此解答。
【详解】分析可知,第n次剪完之后还剩下它的。
当n=7时。
=
=
=
++++…+
=1-
≈1-0
=1
所以,按照这样的规律剪下去,第7次剪了后还剩下它的,照这样无限剪下去,一共剪掉的部分会越来越接近1。
【点睛】本题主要考查应用数形结合的思想解决问题,理解一共剪掉的部分等于整体与最后一次剪掉部分的差是解答题目的关键。
10. 12 4n-4
【分析】由图可知,第1个图形有1个正方形,0个直角三角形;第2个图形有2个正方形,(4×1)个直角三角形;第3个图形有3个正方形,(4×2)个直角三角形;第4个图形有4个正方形,(4×3)个直角三角形……以此类推,每增加一个正方形就增加4个直角三角形,那么第n个图形有n个正方形,4×(n-1)个直角三角形,据此解答。
【详解】分析可知,n个正方形可以得到直角三角形的个数为:4×(n-1)
=(4n-4)个
当n=4时。
4n-4
=4×4-4
=16-4
=12(个)
所以,画4个正方形能得到12个直角三角形,画n个正方形能得到(4n-4)个直角三角形。
【点睛】找出正方形个数和直角三角形个数的变化规律是解答题目的关键。
11.46
【分析】根据火柴棒的摆设规律可知,多摆一个正方形就需要加三根火柴棒。
第1个图形需要4根火柴棒;
第2个图形需要4+3×1=4+3=7(根)火柴棒;
第3个图形需要4+3×2=4+6=10(根)火柴棒;
摆n个图形需要4+3×(n 1)(根)火柴棒;
据此,将当n=15,代入上式,计算出数量即可,据此解答。
【详解】根据火柴棒的摆设规律可知:
多摆一个正方形就需要加三根火柴棒,那么第15个图形所需要的火柴即需要:
4+3×(15-1)
=4+3×14
=4+42
=46(根)
【点睛】解答此题的关键,根据给出火柴的摆放,找到后面火柴摆放的规律。
12.0
【分析】观察算式可知,先求括号里面加法,则的值无限接近1,根据极限思想,括号里面的值等于1,据此解答即可。
【详解】
=1-1
=0
【点睛】本题考查极限思想,明确极限思想的运用是解题的关键。
13. 10 16
【分析】把图案标上序号,如下:
1 2 3 4 5 ……
图案 ……
第1行 个数 1 1 2 2 3 ……
第2行 个数 1 2 2 3 3 ……
第3行 个数 1 1 2 2 3 ……
观察图形发现:
(1)第奇数个图案的每行黑色五角星的个数是一样多的,每行有:个黑色五角星,3行则有:个黑色五角星;
(2)第偶数个图案的第一、三行的黑色五角星一样多,这两行共有n个黑色五角星,第二行共有()个,那么一共的个数是:n+=;因为第6个图案和第10个图案都是偶数,将数据代入,计算出结果即可。
【详解】根据分析,第奇数个图案黑色五角星的个数为:;第偶数个图案黑色五角星的个数为:;
当n=6时,(个);
当n=10时,(个);
【点睛】此题考查了数与形的知识,关键能够观察图案每行的数量变化找出规律再解答。
14. 25 22
【分析】第1幅图有1个点,1=6×1-5;
第2幅图有7个点,7=6×2-5;
第3幅图有13个点,13=6×3-5;
……
第n幅图有(6n-5)个点;
据此规律解答。
【详解】规律:第n幅图有(6n-5)个点。
(1)当n=5时
6n-5
=6×5-5
=30-5
=25(个)
第5幅图中有25个点;
(2)6n-5=127
解:6n-5+5=127+5
6n=132
6n÷6=132÷6
n=22
第22幅图中有127个点。
【点睛】通过数与形的结合,从已知的图形或数据中找到规律,并按规律解题。
15.从图中可以看出:
=
=
【解析】略
16.(1)1,3,6,10
3,6,10,15
(2)▲有28个,△有36个
【详解】(1)填表如下:
序号 ① ② ③ ④
▲ 1 3 6 10
△ 3 6 10 15
(2)1+2+3+4+…+7=28(个)
1+2+3+4+…+8=36(个)
答:第7个图形中▲有28个,△有36个.
17.10种
【详解】分类计算如下:当涂黑的两个方格占两角时,有2种涂法;当占两边时,也有2种涂法,当占一边一角时,有4种涂法;当占一角一中心时,有1种涂法;当占一边一中心时,也有1种涂法.
合计共有2+2+4+1+1=10(种)涂法.
18.1,6,15,20,15,6,1
【解析】略
19.(1)
操作的次数 最初 第一次 第二次 第三次 第四次
共有正三角形的个数 1 4 7 10 13
(2)13次 40个
【分析】从表格中的数据,不难发现:多剪一次,多3个正三角形.继而即可求出剪m次后正三角形的个数.
【详解】(1)由图可知没剪的时候,有一个正三角形,以后每剪一次就多出3个正三角形,所以第m次操作后,总的正三角形的个数为3m+1.第三次操作后,正三角形有:3×3+1=10(个),第四次操作后,正三角形有:3×4+1=13(个),由此可以将上表补充完整,如下:
操作的次数 最初 第一次 第二次 第三次 第四次
共有正三角形的个数 1 4 7 10 13
(2)第m次操作后,一共有3m+1个正三角形.当3m+1=40时,3m=39,m=13
答:第13次操作后,一共剪出了40个正三角形.
20.(1)26根
(2)20条
【详解】摆1条“金鱼”需要火柴棒:8根;
摆2条“金鱼”需要火柴棒:8+6=14(根);
摆3条“金鱼”需要火柴棒:8+6+6=20(根);
……
摆n条“金鱼”需要火柴棒:8+6(n﹣1)=(6n+2)根.
(1)摆4条“金鱼”需要火柴棒:
4×6+2
=24+2
=26(根)
答:摆4条“金鱼”需要26根火柴棒.
(2)6n+2=122
6n=120
n=20
答:用122根火柴棒可以摆20条“金鱼”.
21.(1)13
(2)
【分析】通过观察表示数的方法,可以看出图示是用2进制的方式表示出来的,即满2向前进1,按照从右到左的顺序,第几个格的圆就表示2的几减1次方,据此解答。
【详解】(1)由图可知,圆分别在第1、3、4格,所以这个数是20+22+23=13;图中表示的数是13。
(2)24=16,18=24+2,所以圆在第5格和第2个,画图如下:
【点睛】仔细观察图,找出其中规律是解题关键。
22.(1)9
(2)3(k-2)
【解析】略
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
