七年级数学下册(湘教版):4.3平行线的性质(共32张PPT)
文档属性
| 名称 | 七年级数学下册(湘教版):4.3平行线的性质(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-13 00:00:00 | ||
图片预览










文档简介
课件32张PPT。4.3 平行线的性质?1.用平行线的性质进行简单的推理和计算.(重点)
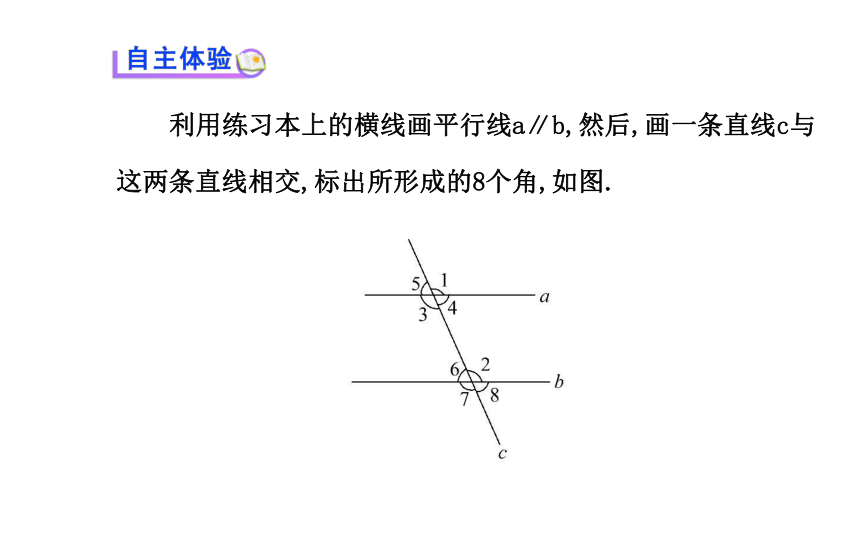
2.掌握平行线的性质及其综合运用.(重点、难点) 利用练习本上的横线画平行线a∥b,然后,画一条直线c与这两条直线相交,标出所形成的8个角,如图.度量这些角的度数,把结果填入表内:【思考】1.在这些角中,∠1和∠2是什么角?这两个角有怎样的数量关系?其他具有这种位置关系的角是否也有这样的数量关系?
提示:同位角 相等 是
2.两条平行线a,b被直线c所截的内错角有什么关系?为什么?
提示:相等.因为a∥b,所以∠1=∠2.
又∠1=∠3,所以∠2=∠3.
又因为∠2+∠6=180°,∠3+∠4=180°,
所以∠4=∠6.3.两条平行线a,b被直线c所截,同旁内角有什么关系?为什么?
提示:互补.因为a∥b,所以∠2=∠3.
又∠3+∠4=180°,所以∠2+∠4=180°.
又因为∠2+∠6=180°,
所以∠3+∠6=180°.【总结】平行线的性质:
(1)两直线平行,同位角_____.
(2)两直线平行,内错角_____.
(3)两直线平行,同旁内角_____.相等相等互补 (打“√”或“×”)
(1)两条直线被第三条直线所截,同位角一定相等.( )
(2)两条平行直线被第三条直线所截,同旁内角互补.( )
(3)两条平行直线被第三条直线所截,一对内错角的平分线互相
平行.( )
(4)从两直线平行得到角的数量关系,是平行线的性质.( )×√√√知识点 1 平行线的性质?
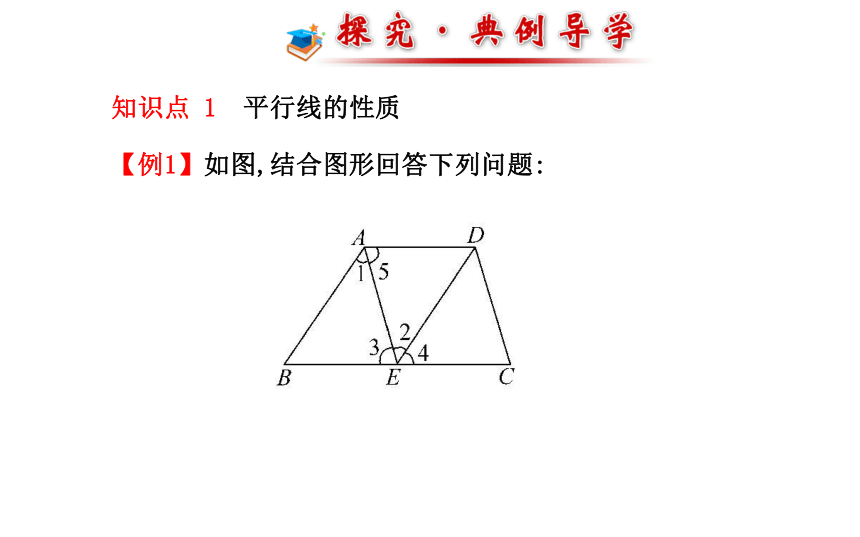
【例1】如图,结合图形回答下列问题:(1)如果AB∥DE,可判断∠1和∠2有何关系,根据是什么?
(2)如果AE∥DC,可判断∠3和∠C有何关系,根据是什么?
(3)如果AD∥BE,可判断∠5与∠3有何关系,根据是什么?
(4)如果AB∥DE,可判断∠B与∠BED有何关系,根据是什么?【思路点拨】两平行直线的位置→两角的位置→平行线性质→两角数量关系→写根据.
【自主解答】(1)∠1=∠2,根据:两直线平行,内错角相等.
(2)∠3=∠C,根据:两直线平行,同位角相等.
(3)∠5=∠3,根据:两直线平行,内错角相等.
(4)∠B+∠BED =180°,根据:两直线平行,同旁内角互补.【总结提升】平行线性质的直接应用的关键和方法
1.关键:判断出所确定两个角的位置关系,然后确定两角相等或互补.
2.方法:两平行线是被截线,两角公共边(在同一直线上的边)是截线,依此可确定两个角的位置关系.知识点 2 平行线性质的综合应用?
【例2】(2013·盐城中考)如图,直线a∥b,∠1=120°,∠2=40°,则∠3等
于( )
A.60° B.70°
C.80° D.90°【思路点拨】先由对顶角相等,求出∠3的内错角,再由平行线的性质求出∠3.
【自主解答】选C.如图,由对顶角相等得∠2+∠4=∠1=120°,又∠2=40°,所以∠4=80°,由a∥b得,
∠3=∠4=80°.【总结提升】平行线性质的间接应用的几种类型
1.求相关角的余角或补角.
2.与角平分线有关的计算.
3.添加辅助线构造平行线,求相关角的度数.题组一:平行线的性质
1.(2013·晋江中考)如图,已知直线a∥b,直线c与a,b分别交点于A,B,∠1=50°,则∠2=( )
A.40° B.50° C.100° D.130°
【解析】选B.根据两直线平行同位角相等,得到∠2=∠1=50°.2.(2013·衡阳中考)如图,AB∥CD,如果
∠B=20°,那么∠C为( )
A.40° B.20°
C.60° D.70°
【解析】选B.根据两直线平行,内错角相等可以得到∠C=20°.3.(2013·湖州中考)如图,已知直线a,b被直线c所截,a∥b,
∠1=60°,则∠2的度数为( )
A.30° B.60° C.120° D.150°
【解析】选C.如图,因为a∥b,所以∠1+∠3=180°,所以∠3=120°,所以∠2=∠3=120°.4.如图,AB∥CD,∠DCE=80°,则∠BEF=( )
A.120° B.110° C.100° D.80°
【解析】选C.因为AB∥CD,所以∠DCE+∠BEF=180°,因为∠DCE=80°,所以∠BEF=180°-80°=100°.5.两条平行线被第三条直线所截,如果一对同旁内角的度数之比为3∶7,那么这两个角的度数分别是( )
A.30°,70° B.60°,140°
C.54°,126° D.64°,116°
【解析】选C.设这两个角分别是3x°和7x°,由两直线平行同旁内角互补,得3x+7x=180,x=18,所以3×18°=54°,7×18°
=126°.6.如图所示,AB∥DE,DF∥BC,∠1=62°.求∠2,∠3的度数.
【解析】因为DF∥BC,∠1=62°,所以∠2=180°-∠1=180°-62°=118°(两直线平行,同旁内角互补).
因为AB∥DE,
所以∠3=∠2=118°(两直线平行,同位角相等).题组二:平行线性质的综合应用
1.(2013·白银中考)如图,把一块含有
45°的直角三角板的两个顶点放在直
尺的对边上.如果∠1=20°,那么∠2
的度数是( )
A.15° B.20° C.25° D.30°
【解析】选C.由直尺的两边沿平行可知,
∠3=∠1=20°.又∠2+∠3=45°,所以
∠2=25°.2.(2013·枣庄中考)如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
A.140° B.60° C.50° D.40°
【解析】选D.因为∠CDE=140°,所以∠CDA=40°,又因为AB∥CD,所以∠A=∠CDA=40°.3.如图,已知AB∥CD,则图中与
∠1互补的角有( )
A.2个 B.3个
C.4个 D.5个
【解析】选A.因为AB∥CD,所以∠1+∠AEF=180°,又因为∠1+∠EFD=180°.所以图中与∠1互补的角有2个.4.如图,已知直线AB∥CD,BE平分∠ABC,交CD
于点D,∠CDE=150°,则∠C的度数为( )
A.150° B.130°
C.120° D.100°
【解析】选C.因为∠EDC=150°,所以∠CDB=30°.因为AB∥CD,
所以∠ABD=∠CDB=30°.因为BE平分∠ABC,所以∠ABD=∠CBD=
30°.
所以∠ABC=60°,又AB∥CD,所以∠C=180°-∠ABC=120°.5.如图,已知a∥b,∠1=45°,则∠2= .
【解析】如图,因为a∥b,所以∠3=∠1=45°,因为∠3+∠2=
180°,所以∠2=135°.
答案:135°6.如图,FE∥ON,OE平分∠MON,∠FEO=28°,则∠MFE=_____度.
【解析】因为FE∥ON,所以∠NOE=∠FEO=28°.因为OE平分∠MON,所以∠MON=56°.又因为FE∥ON,所以∠MFE=∠MON=56°.
答案:567.如图所示,小张从家(图中A处)出发,向南
偏东40°的方向走到学校(图中B处),再从
学校出发,向北偏西75°的方向走到小明
家(图中C处),试问∠ABC为多少度?
【解析】由题意,得DB∥AE,
所以∠DBA=∠EAB=40°,
又因为∠CBD=75°,
所以∠ABC=∠CBD-∠DBA=75°-40°=35°.【想一想错在哪?】珠江流域某江段江水流向经过B,C,D三点
拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE= 度.提示:没有根据平行线的性质解答.
2.掌握平行线的性质及其综合运用.(重点、难点) 利用练习本上的横线画平行线a∥b,然后,画一条直线c与这两条直线相交,标出所形成的8个角,如图.度量这些角的度数,把结果填入表内:【思考】1.在这些角中,∠1和∠2是什么角?这两个角有怎样的数量关系?其他具有这种位置关系的角是否也有这样的数量关系?
提示:同位角 相等 是
2.两条平行线a,b被直线c所截的内错角有什么关系?为什么?
提示:相等.因为a∥b,所以∠1=∠2.
又∠1=∠3,所以∠2=∠3.
又因为∠2+∠6=180°,∠3+∠4=180°,
所以∠4=∠6.3.两条平行线a,b被直线c所截,同旁内角有什么关系?为什么?
提示:互补.因为a∥b,所以∠2=∠3.
又∠3+∠4=180°,所以∠2+∠4=180°.
又因为∠2+∠6=180°,
所以∠3+∠6=180°.【总结】平行线的性质:
(1)两直线平行,同位角_____.
(2)两直线平行,内错角_____.
(3)两直线平行,同旁内角_____.相等相等互补 (打“√”或“×”)
(1)两条直线被第三条直线所截,同位角一定相等.( )
(2)两条平行直线被第三条直线所截,同旁内角互补.( )
(3)两条平行直线被第三条直线所截,一对内错角的平分线互相
平行.( )
(4)从两直线平行得到角的数量关系,是平行线的性质.( )×√√√知识点 1 平行线的性质?
【例1】如图,结合图形回答下列问题:(1)如果AB∥DE,可判断∠1和∠2有何关系,根据是什么?
(2)如果AE∥DC,可判断∠3和∠C有何关系,根据是什么?
(3)如果AD∥BE,可判断∠5与∠3有何关系,根据是什么?
(4)如果AB∥DE,可判断∠B与∠BED有何关系,根据是什么?【思路点拨】两平行直线的位置→两角的位置→平行线性质→两角数量关系→写根据.
【自主解答】(1)∠1=∠2,根据:两直线平行,内错角相等.
(2)∠3=∠C,根据:两直线平行,同位角相等.
(3)∠5=∠3,根据:两直线平行,内错角相等.
(4)∠B+∠BED =180°,根据:两直线平行,同旁内角互补.【总结提升】平行线性质的直接应用的关键和方法
1.关键:判断出所确定两个角的位置关系,然后确定两角相等或互补.
2.方法:两平行线是被截线,两角公共边(在同一直线上的边)是截线,依此可确定两个角的位置关系.知识点 2 平行线性质的综合应用?
【例2】(2013·盐城中考)如图,直线a∥b,∠1=120°,∠2=40°,则∠3等
于( )
A.60° B.70°
C.80° D.90°【思路点拨】先由对顶角相等,求出∠3的内错角,再由平行线的性质求出∠3.
【自主解答】选C.如图,由对顶角相等得∠2+∠4=∠1=120°,又∠2=40°,所以∠4=80°,由a∥b得,
∠3=∠4=80°.【总结提升】平行线性质的间接应用的几种类型
1.求相关角的余角或补角.
2.与角平分线有关的计算.
3.添加辅助线构造平行线,求相关角的度数.题组一:平行线的性质
1.(2013·晋江中考)如图,已知直线a∥b,直线c与a,b分别交点于A,B,∠1=50°,则∠2=( )
A.40° B.50° C.100° D.130°
【解析】选B.根据两直线平行同位角相等,得到∠2=∠1=50°.2.(2013·衡阳中考)如图,AB∥CD,如果
∠B=20°,那么∠C为( )
A.40° B.20°
C.60° D.70°
【解析】选B.根据两直线平行,内错角相等可以得到∠C=20°.3.(2013·湖州中考)如图,已知直线a,b被直线c所截,a∥b,
∠1=60°,则∠2的度数为( )
A.30° B.60° C.120° D.150°
【解析】选C.如图,因为a∥b,所以∠1+∠3=180°,所以∠3=120°,所以∠2=∠3=120°.4.如图,AB∥CD,∠DCE=80°,则∠BEF=( )
A.120° B.110° C.100° D.80°
【解析】选C.因为AB∥CD,所以∠DCE+∠BEF=180°,因为∠DCE=80°,所以∠BEF=180°-80°=100°.5.两条平行线被第三条直线所截,如果一对同旁内角的度数之比为3∶7,那么这两个角的度数分别是( )
A.30°,70° B.60°,140°
C.54°,126° D.64°,116°
【解析】选C.设这两个角分别是3x°和7x°,由两直线平行同旁内角互补,得3x+7x=180,x=18,所以3×18°=54°,7×18°
=126°.6.如图所示,AB∥DE,DF∥BC,∠1=62°.求∠2,∠3的度数.
【解析】因为DF∥BC,∠1=62°,所以∠2=180°-∠1=180°-62°=118°(两直线平行,同旁内角互补).
因为AB∥DE,
所以∠3=∠2=118°(两直线平行,同位角相等).题组二:平行线性质的综合应用
1.(2013·白银中考)如图,把一块含有
45°的直角三角板的两个顶点放在直
尺的对边上.如果∠1=20°,那么∠2
的度数是( )
A.15° B.20° C.25° D.30°
【解析】选C.由直尺的两边沿平行可知,
∠3=∠1=20°.又∠2+∠3=45°,所以
∠2=25°.2.(2013·枣庄中考)如图,AB∥CD,∠CDE=140°,则∠A的度数为( )
A.140° B.60° C.50° D.40°
【解析】选D.因为∠CDE=140°,所以∠CDA=40°,又因为AB∥CD,所以∠A=∠CDA=40°.3.如图,已知AB∥CD,则图中与
∠1互补的角有( )
A.2个 B.3个
C.4个 D.5个
【解析】选A.因为AB∥CD,所以∠1+∠AEF=180°,又因为∠1+∠EFD=180°.所以图中与∠1互补的角有2个.4.如图,已知直线AB∥CD,BE平分∠ABC,交CD
于点D,∠CDE=150°,则∠C的度数为( )
A.150° B.130°
C.120° D.100°
【解析】选C.因为∠EDC=150°,所以∠CDB=30°.因为AB∥CD,
所以∠ABD=∠CDB=30°.因为BE平分∠ABC,所以∠ABD=∠CBD=
30°.
所以∠ABC=60°,又AB∥CD,所以∠C=180°-∠ABC=120°.5.如图,已知a∥b,∠1=45°,则∠2= .
【解析】如图,因为a∥b,所以∠3=∠1=45°,因为∠3+∠2=
180°,所以∠2=135°.
答案:135°6.如图,FE∥ON,OE平分∠MON,∠FEO=28°,则∠MFE=_____度.
【解析】因为FE∥ON,所以∠NOE=∠FEO=28°.因为OE平分∠MON,所以∠MON=56°.又因为FE∥ON,所以∠MFE=∠MON=56°.
答案:567.如图所示,小张从家(图中A处)出发,向南
偏东40°的方向走到学校(图中B处),再从
学校出发,向北偏西75°的方向走到小明
家(图中C处),试问∠ABC为多少度?
【解析】由题意,得DB∥AE,
所以∠DBA=∠EAB=40°,
又因为∠CBD=75°,
所以∠ABC=∠CBD-∠DBA=75°-40°=35°.【想一想错在哪?】珠江流域某江段江水流向经过B,C,D三点
拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE= 度.提示:没有根据平行线的性质解答.
