七年级数学下册(湘教版):4.5垂线(共37张PPT)
文档属性
| 名称 | 七年级数学下册(湘教版):4.5垂线(共37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-13 22:02:09 | ||
图片预览









文档简介
课件37张PPT。4.5 垂 线?1.垂线的概念、性质.(重点)
2.垂线的性质及应用.(重点、难点)一、垂直的定义
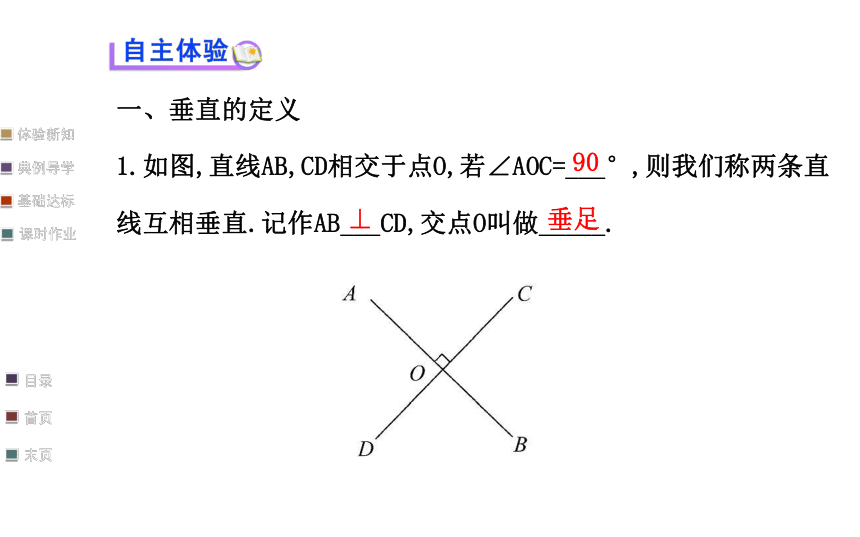
1.如图,直线AB,CD相交于点O,若∠AOC=___°,则我们称两条直
线互相垂直.记作AB___CD,交点O叫做_____.90⊥垂足2.(1)应用格式:
因为∠AOC= _____,
所以AB⊥CD(垂直的定义).
(2)反之,如果AB⊥CD,那么∠AOC= _____.90°90°二、垂线的画法及性质
【思考】1.画已知直线l的垂线能画几条?
提示:无数条.
2.在平面内,过直线l上的一点A画直线l的垂线,这样的垂线能画
___条.
3.在平面内,过直线l外的一点B画直线l的垂线,这样的垂线能画
___条.一一4.量一量,比一比.
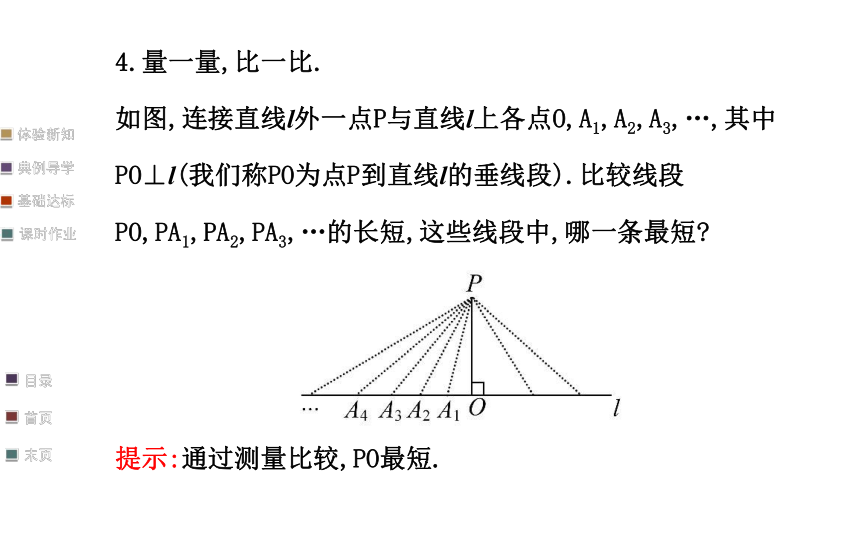
如图,连接直线l外一点P与直线l上各点O,A1,A2,A3,…,其中PO⊥l(我们称PO为点P到直线l的垂线段).比较线段PO,PA1,PA2,PA3,…的长短,这些线段中,哪一条最短?
提示:通过测量比较,PO最短.【总结】1.在同一平面内,过一点_________一条直线与已知直
线垂直.
2.直线外一点与直线上各点连接的所有线段中,_______最短.
简单地说成:_______最短.有且只有垂线段垂线段三、点到直线的距离
从直线外一点到这条直线的_______的长度.垂线段 (打“√”或“×”)
(1)点到直线的距离是点到直线的垂线段.( )
(2)一条直线只有一条垂线.( )
(3)同一平面内,一条直线不可能与两条相交直线都垂直.( )
(4)垂线段最短.( )
(5)两条直线互相垂直,则这两条直线所形成的四个角都是直角.
( )××√√√知识点 1 垂直的定义及应用?
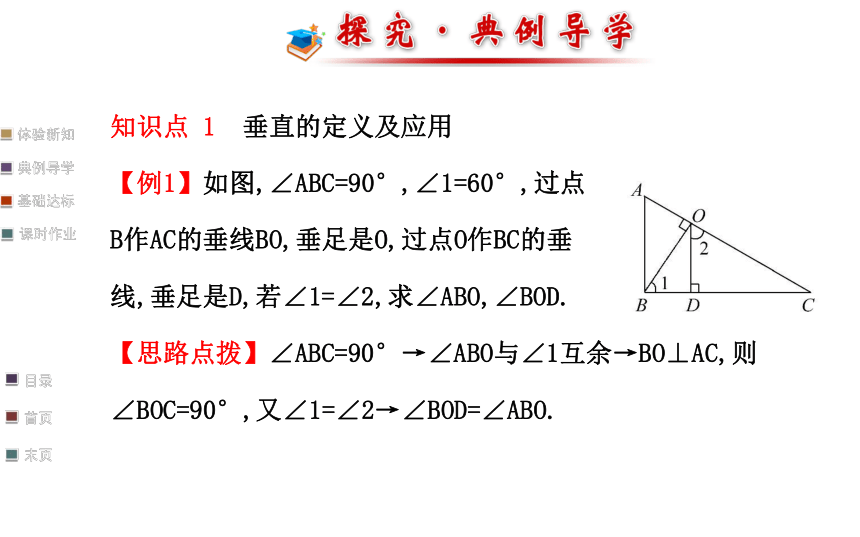
【例1】如图,∠ABC=90°,∠1=60°,过点
B作AC的垂线BO,垂足是O,过点O作BC的垂
线,垂足是D,若∠1=∠2,求∠ABO,∠BOD.
【思路点拨】∠ABC=90°→∠ABO与∠1互余→BO⊥AC,则∠BOC=90°,又∠1=∠2→∠BOD=∠ABO.【自主解答】因为∠ABC=90°,∠1=60°,
所以∠ABO=30°.
因为BO⊥AC于O点,所以∠BOC=90°,
又因为∠2=∠1,所以∠BOD=∠ABO=30°.
【总结提升】垂直的定义的双重性
垂直的定义既是性质又是判定:一是可以由垂直关系得到角的数量关系;二是根据角的数量关系判定角的边所在直线的位置关系.知识点 2 垂线的画法及性质的应用?
【例2】如图,点A表示小明家,点B表示小明外婆家,若小明先去外婆家拿渔具,然后再去河边钓鱼,怎样走路最短,请画出行走路径,并说明理由.【解题探究】
1.小明的行走路径分哪几步?
提示:小明家→外婆家→河边.
2.小明从家去外婆家,转化为数学问题即两点之间的问题,应怎样走最近?理由是什么?
提示:最短路径是线段AB,理由是两点之间线段最短.3.小明从外婆家去河边,转化为数学问题即点到直线的距离的问题,应怎样走最近?理由是什么?
提示:最短路径是过点B作河岸的垂线,点B和垂足间的线段最短,理由是垂线段最短.
如图【总结提升】垂线画法三字诀
1.一靠:靠已知直线,使三角尺的一条直角边与已知直线重合.
2.二移:沿已知直线移动三角尺,使另一条直角边过已知的定点.
3.三画:画已知直线的垂线.题组一:垂直的定义及应用
1.下列时刻中,时针与分针互相垂直的是( )
A.2点20分 B.3点整
C.12点10分 D.5点40分
【解析】选B.在钟表的表面上,相邻数字(如1和2)与表中心连线的夹角为30°,而3点整时,时针指向3,分针指向12,故在3点整时时针与分针的夹角为直角.2.如图,直线AB,CD相交于点O,OE⊥AB于O,∠COE=55°,则∠BOD的度数是( )
A.40° B.45° C.30° D.35°
【解析】选D.因为OE⊥AB,∠COE=55°,所以∠AOC=90°-∠COE=35°;因为∠BOD与∠AOC是对顶角,所以∠BOD=∠AOC=35°.3.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余
C.互补 D.互为对顶角【解析】选B.因为∠2=∠COE(对顶角相等),
又因为AB⊥CD,所以∠1+∠COE=90°,
所以∠1+∠2=90°,所以两角互余.4.如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1=27°,则∠2= ,∠FOB= .
【解析】因为AB⊥CD,所以∠AOD=∠BOD=90°,
所以∠2=90°-∠1=63°,∠FOB=∠1+∠BOD=117°.
答案:63° 117°5.如图,∠ABD=90°,直线 ⊥直线 ,垂足为 ,在平面内,过D点有且只有 条直线
与直线AC垂直.
【解析】根据垂线的性质可知,直线AC⊥直线BD,垂足为B,在平面内,过D点有且只有1条直线DB与直线AC垂直.
答案:AC BD B 1 DB6.如图,直线AB,CD相交于点O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC,∠BOF的度数.【解析】因为OE⊥CD于点O,∠1=50°,
所以∠AOD=90°-∠1=40°,
因为∠BOC与∠AOD是对顶角,
所以∠BOC=∠AOD=40°.
因为OD平分∠AOF,
所以∠DOF=∠AOD=40°,
所以∠BOF=180°-∠DOA-∠DOF
=180°-40°-40°=100°.7.如图,AB,CD相交于O点,若∠EOD=40°,
∠BOC=130°,猜想射线OE与直线AB的位
置关系,并说明理由.
【解析】OE⊥AB.理由如下:
因为∠BOC=130°(已知),
所以∠AOD=∠BOC=130°(对顶角相等),
所以∠AOE=∠AOD-∠EOD=130°-40°=90°.
所以OE⊥AB.题组二:垂线的画法及性质的应用
1.如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是( )
A.2.5 B.3 C.4 D.5
【解析】选A.因为AC是BC上的垂线段,所以点A到BC的最短距离是3,故不可能是2.5.2.下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
【解析】选A.点P到直线MN的距离应是垂线段PQ的长度,PQ⊥MN,故选A.3.画一条线段的垂线,垂足在( )
A.线段上 B.线段的端点处
C.线段的延长线上 D.以上都有可能
【解析】选D.线段的垂线有无数条,过一点画线段的垂线,垂足可以在线段上,在线段的端点处,在线段的延长线上,故选D.4.如图,从书店到公路最近的是 号路线,数学道理是 .
【解析】①号路线最近,理由是垂线段最短.
答案:① 垂线段最短5.如图是小亮同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 的长度.
【解析】因为身体在沙坑上所有接触的点中,距离起跳线最近的点到起跳线的距离作为跳远成绩,所以他的跳远成绩是线段BN的长度.
答案:BN6.如图所示,AB是一条河流,要铺设管道将河水引到C,D两个用水点,现有两种铺设管道的方案.
方案一:分别过C,D作AB的垂线,垂足分别为E,F,沿CE,DF铺设管道;
方案二:连结CD交AB于点P,沿PC,PD铺设管道.
这两种铺设管道的方案哪一种更节省材料?为什么?【解析】按方案一铺设管道更节省材料.理由如下:因为CE⊥AB,
DF⊥AB,而AB与CD不垂直,所以根据“垂线段最短”,可知CEDF(2)两点确定一条直线
(3)连接直线外一点与直线上各点的所有线段中,垂线段最短【想一想错在哪?】如图所示,AD⊥BD,BC⊥CD,AB=5cm,BC
=3cm,则BD的长度的取值范围是( )
A.大于3cm B.小于5cm
C.大于3cm或小于5cm D.大于3cm且小于5cm提示:分析问题不全面!
2.垂线的性质及应用.(重点、难点)一、垂直的定义
1.如图,直线AB,CD相交于点O,若∠AOC=___°,则我们称两条直
线互相垂直.记作AB___CD,交点O叫做_____.90⊥垂足2.(1)应用格式:
因为∠AOC= _____,
所以AB⊥CD(垂直的定义).
(2)反之,如果AB⊥CD,那么∠AOC= _____.90°90°二、垂线的画法及性质
【思考】1.画已知直线l的垂线能画几条?
提示:无数条.
2.在平面内,过直线l上的一点A画直线l的垂线,这样的垂线能画
___条.
3.在平面内,过直线l外的一点B画直线l的垂线,这样的垂线能画
___条.一一4.量一量,比一比.
如图,连接直线l外一点P与直线l上各点O,A1,A2,A3,…,其中PO⊥l(我们称PO为点P到直线l的垂线段).比较线段PO,PA1,PA2,PA3,…的长短,这些线段中,哪一条最短?
提示:通过测量比较,PO最短.【总结】1.在同一平面内,过一点_________一条直线与已知直
线垂直.
2.直线外一点与直线上各点连接的所有线段中,_______最短.
简单地说成:_______最短.有且只有垂线段垂线段三、点到直线的距离
从直线外一点到这条直线的_______的长度.垂线段 (打“√”或“×”)
(1)点到直线的距离是点到直线的垂线段.( )
(2)一条直线只有一条垂线.( )
(3)同一平面内,一条直线不可能与两条相交直线都垂直.( )
(4)垂线段最短.( )
(5)两条直线互相垂直,则这两条直线所形成的四个角都是直角.
( )××√√√知识点 1 垂直的定义及应用?
【例1】如图,∠ABC=90°,∠1=60°,过点
B作AC的垂线BO,垂足是O,过点O作BC的垂
线,垂足是D,若∠1=∠2,求∠ABO,∠BOD.
【思路点拨】∠ABC=90°→∠ABO与∠1互余→BO⊥AC,则∠BOC=90°,又∠1=∠2→∠BOD=∠ABO.【自主解答】因为∠ABC=90°,∠1=60°,
所以∠ABO=30°.
因为BO⊥AC于O点,所以∠BOC=90°,
又因为∠2=∠1,所以∠BOD=∠ABO=30°.
【总结提升】垂直的定义的双重性
垂直的定义既是性质又是判定:一是可以由垂直关系得到角的数量关系;二是根据角的数量关系判定角的边所在直线的位置关系.知识点 2 垂线的画法及性质的应用?
【例2】如图,点A表示小明家,点B表示小明外婆家,若小明先去外婆家拿渔具,然后再去河边钓鱼,怎样走路最短,请画出行走路径,并说明理由.【解题探究】
1.小明的行走路径分哪几步?
提示:小明家→外婆家→河边.
2.小明从家去外婆家,转化为数学问题即两点之间的问题,应怎样走最近?理由是什么?
提示:最短路径是线段AB,理由是两点之间线段最短.3.小明从外婆家去河边,转化为数学问题即点到直线的距离的问题,应怎样走最近?理由是什么?
提示:最短路径是过点B作河岸的垂线,点B和垂足间的线段最短,理由是垂线段最短.
如图【总结提升】垂线画法三字诀
1.一靠:靠已知直线,使三角尺的一条直角边与已知直线重合.
2.二移:沿已知直线移动三角尺,使另一条直角边过已知的定点.
3.三画:画已知直线的垂线.题组一:垂直的定义及应用
1.下列时刻中,时针与分针互相垂直的是( )
A.2点20分 B.3点整
C.12点10分 D.5点40分
【解析】选B.在钟表的表面上,相邻数字(如1和2)与表中心连线的夹角为30°,而3点整时,时针指向3,分针指向12,故在3点整时时针与分针的夹角为直角.2.如图,直线AB,CD相交于点O,OE⊥AB于O,∠COE=55°,则∠BOD的度数是( )
A.40° B.45° C.30° D.35°
【解析】选D.因为OE⊥AB,∠COE=55°,所以∠AOC=90°-∠COE=35°;因为∠BOD与∠AOC是对顶角,所以∠BOD=∠AOC=35°.3.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余
C.互补 D.互为对顶角【解析】选B.因为∠2=∠COE(对顶角相等),
又因为AB⊥CD,所以∠1+∠COE=90°,
所以∠1+∠2=90°,所以两角互余.4.如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1=27°,则∠2= ,∠FOB= .
【解析】因为AB⊥CD,所以∠AOD=∠BOD=90°,
所以∠2=90°-∠1=63°,∠FOB=∠1+∠BOD=117°.
答案:63° 117°5.如图,∠ABD=90°,直线 ⊥直线 ,垂足为 ,在平面内,过D点有且只有 条直线
与直线AC垂直.
【解析】根据垂线的性质可知,直线AC⊥直线BD,垂足为B,在平面内,过D点有且只有1条直线DB与直线AC垂直.
答案:AC BD B 1 DB6.如图,直线AB,CD相交于点O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC,∠BOF的度数.【解析】因为OE⊥CD于点O,∠1=50°,
所以∠AOD=90°-∠1=40°,
因为∠BOC与∠AOD是对顶角,
所以∠BOC=∠AOD=40°.
因为OD平分∠AOF,
所以∠DOF=∠AOD=40°,
所以∠BOF=180°-∠DOA-∠DOF
=180°-40°-40°=100°.7.如图,AB,CD相交于O点,若∠EOD=40°,
∠BOC=130°,猜想射线OE与直线AB的位
置关系,并说明理由.
【解析】OE⊥AB.理由如下:
因为∠BOC=130°(已知),
所以∠AOD=∠BOC=130°(对顶角相等),
所以∠AOE=∠AOD-∠EOD=130°-40°=90°.
所以OE⊥AB.题组二:垂线的画法及性质的应用
1.如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是( )
A.2.5 B.3 C.4 D.5
【解析】选A.因为AC是BC上的垂线段,所以点A到BC的最短距离是3,故不可能是2.5.2.下列图形中,线段PQ的长表示点P到直线MN的距离的是( )
【解析】选A.点P到直线MN的距离应是垂线段PQ的长度,PQ⊥MN,故选A.3.画一条线段的垂线,垂足在( )
A.线段上 B.线段的端点处
C.线段的延长线上 D.以上都有可能
【解析】选D.线段的垂线有无数条,过一点画线段的垂线,垂足可以在线段上,在线段的端点处,在线段的延长线上,故选D.4.如图,从书店到公路最近的是 号路线,数学道理是 .
【解析】①号路线最近,理由是垂线段最短.
答案:① 垂线段最短5.如图是小亮同学在体育课上跳远后留下的脚印,他的跳远成绩是线段 的长度.
【解析】因为身体在沙坑上所有接触的点中,距离起跳线最近的点到起跳线的距离作为跳远成绩,所以他的跳远成绩是线段BN的长度.
答案:BN6.如图所示,AB是一条河流,要铺设管道将河水引到C,D两个用水点,现有两种铺设管道的方案.
方案一:分别过C,D作AB的垂线,垂足分别为E,F,沿CE,DF铺设管道;
方案二:连结CD交AB于点P,沿PC,PD铺设管道.
这两种铺设管道的方案哪一种更节省材料?为什么?【解析】按方案一铺设管道更节省材料.理由如下:因为CE⊥AB,
DF⊥AB,而AB与CD不垂直,所以根据“垂线段最短”,可知CE
(3)连接直线外一点与直线上各点的所有线段中,垂线段最短【想一想错在哪?】如图所示,AD⊥BD,BC⊥CD,AB=5cm,BC
=3cm,则BD的长度的取值范围是( )
A.大于3cm B.小于5cm
C.大于3cm或小于5cm D.大于3cm且小于5cm提示:分析问题不全面!
