中考数学思维方法讲义:第2讲 证明--四边形专题(含答案)
文档属性
| 名称 | 中考数学思维方法讲义:第2讲 证明--四边形专题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 224.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-27 08:01:11 | ||
图片预览



文档简介
§第2讲 证明(四边形专题)
【学习目标】
1、牢记四边形的有关性质及其判定;
2、运用四边形的性质及判定进行有关计算与证明;
3、数学思想方法的合理运用。
【考点透视】
1.平行四边形的性质及判定方法。 2.矩形的性质及判定方法。
3.菱形的性质及判定方法。 4.正方形的性质及判定方法。
5.梯形的概念及判定方法。 6.梯形问题的转化。
【数学思想方法】
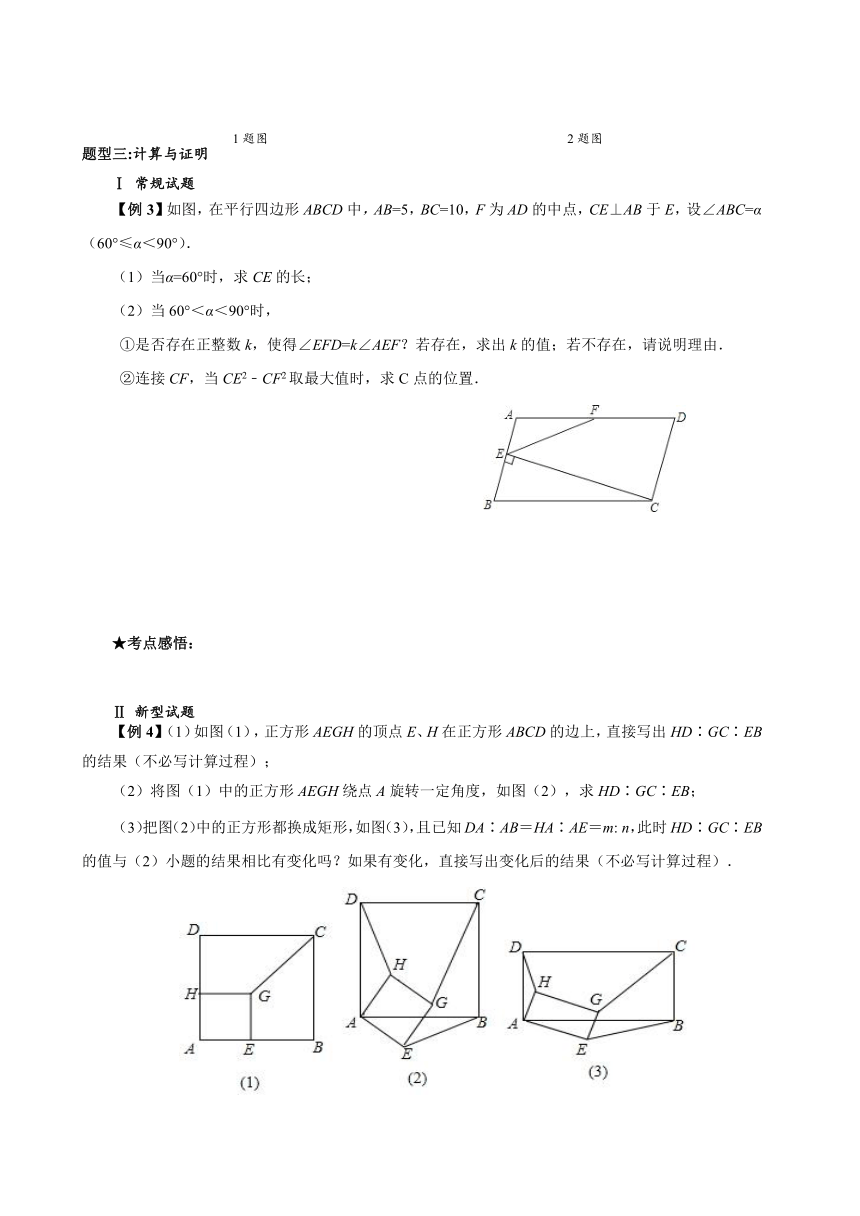
§Ⅰ梯形的常见辅助线的添加方法:
通过添加辅助线,把梯形转化成平行四边形和三角形.(作高、平移腰、延腰、平移对角线、等积变化)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
§Ⅱ一招制胜——图形分离法
【精彩知识】
题型一: 选择题
【例1】如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则阴影部分的面积是( )
A. B.2 C.3 D.
★考点感悟:
●变式练习:
1、如图,菱形ABCD中,AB=2,∠A ( http: / / www.21cnjy.com )=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
A. 1 B. C. 2 D.+1
2、如图,梯形ABCD中,AB∥CD,点 ( http: / / www.21cnjy.com )E、F、G分别是BD、AC、DC的中点.已知两底差是6,两腰和是12,则△EFG的周长是( )
A.8 B.9 C.10 D.12
3、在面积为15的平行四边 ( http: / / www.21cnjy.com )形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A.11+ B.11-
C.11+或11- D.11-或1+
题型二:填空题
【例2】如图,菱形ABCD中,AB=A ( http: / / www.21cnjy.com )C,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH,④AD 2=OD·DH中,正确的结论是 .
●变式练习:
1. 如图,线段AC=n+1(其中 ( http: / / www.21cnjy.com )n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为Sn.当n≥2时,Sn﹣Sn﹣1= .
2、如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2= 。
1题图 2题图
题型三:计算与证明
Ⅰ 常规试题
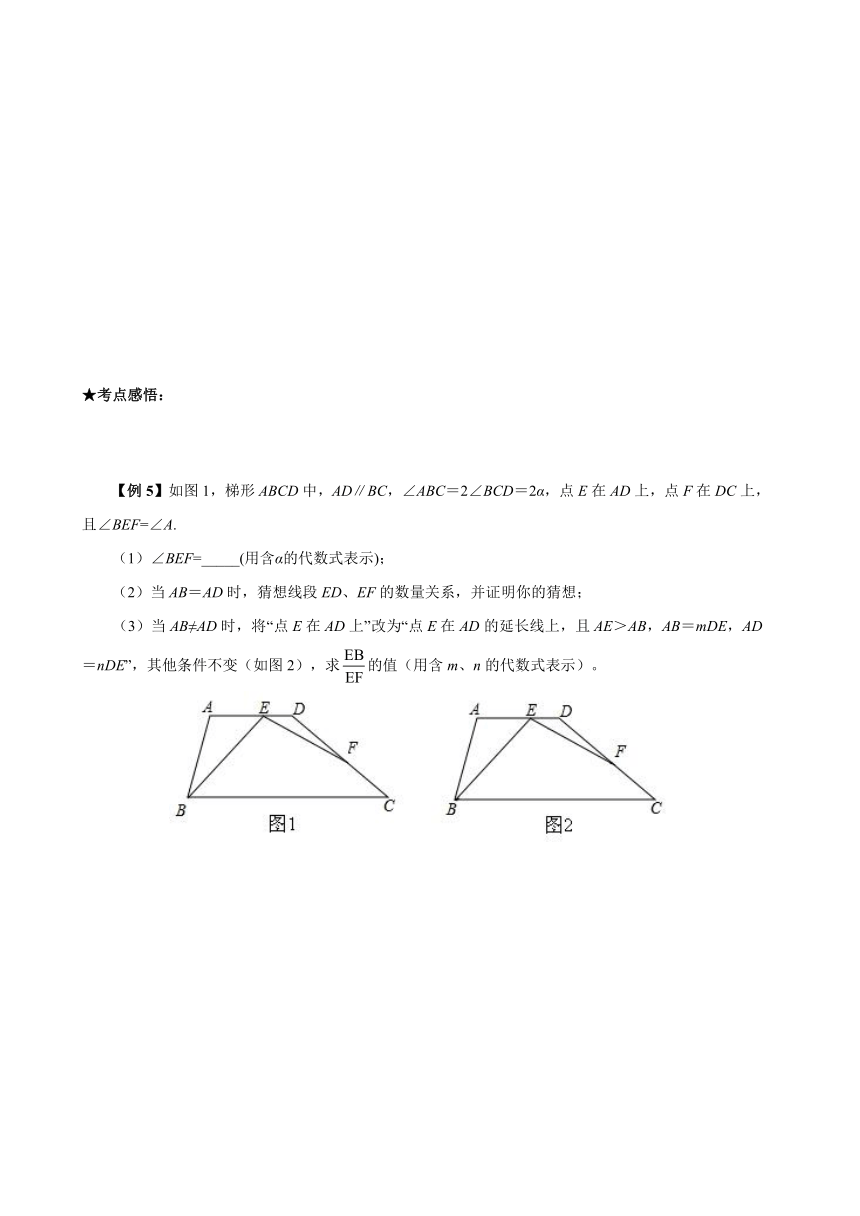
【例3】如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2﹣CF2取最大值时,求C点的位置.
★考点感悟:
Ⅱ 新型试题
【例4】(1)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD∶GC∶EB的结果(不必写计算过程);
(2)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD∶GC∶EB;
(3)把图(2)中的正方形都换成矩形,如图( ( http: / / www.21cnjy.com )3),且已知DA∶AB=HA∶AE=m: n,此时HD∶GC∶EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).
( http: / / www.21cnjy.com )
★考点感悟:
【例5】如图1,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点E在AD上,点F在DC上,且∠BEF=∠A.
(1)∠BEF=_____(用含α的代数式表示);
(2)当AB=AD时,猜想线段ED、EF的数量关系,并证明你的猜想;
(3)当AB≠AD时,将“点E在AD上”改为“点E在AD的延长线上,且AE>AB,AB=mDE,AD=nDE”,其他条件不变(如图2),求的值(用含m、n的代数式表示)。
( http: / / www.21cnjy.com )
★考点感悟:
【例6】如图,在矩形OAB ( http: / / www.21cnjy.com )C中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发 ( http: / / www.21cnjy.com ),沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物 ( http: / / www.21cnjy.com )线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
★考点感悟:
【课后测试】
1、如图,四边形ABCD中,∠BAD= ( http: / / www.21cnjy.com )120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
A. 130° B. 120° C. 110° D. 100°
2、如图,在直角梯形ABCD中,A ( http: / / www.21cnjy.com )D//BC,∠C=90°,AD=5,BC=9, 以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )
A.10 B.11 C.12 D.13
3、如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(1)求证:△BDG∽△DEG;
(2)若EG BG=4,求BE的长.
4、如图,梯形ABCD中,AD∥BC,∠ ( http: / / www.21cnjy.com )DCB=45°,CD =2,BD⊥CD .过点C作CE⊥AB于E,对角线BD于F.点G为BC中点,连结EG、AF.
(1)求EG的长;
(2)求证:CF =AB +AF.
5、如图1,在菱形ABCD中,AC=2,BD=2 3 ,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角 ( http: / / www.21cnjy.com )板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
( http: / / www.21cnjy.com )
部分答案与提示:
【例1】如图,设BF、CE相交于点M,
∵菱形ABCD和菱形ECGF的边长分别为2和3,
∴△BCM∽△BGF,∴,即。
解得CM=1.2。∴DM=2﹣1.2=0.8。
∵∠A=120°,∴∠ABC=180°﹣120°=60°。
∴菱形ABCD边CD上的高为2sin60°=2×,
菱形ECGF边CE上的高为3sin60°=3×。
∴阴影部分面积=S△BDM+S△DFM=×0.8×+×0.8×。故选A。
【例3】解:(1)∵α=60°,BC=10,∴sinα=,即sin60°=,解得CE=。
(2)①存在k=3,使得∠EFD=k∠AEF。理由如下:
连接CF并延长交BA的延长线于点G,
∵F为AD的中点,∴AF=FD。
在平行四边形ABCD中,AB∥CD,∴∠G=∠DCF。
在△AFG和△CFD中,
∵∠G=∠DCF, ∠G=∠DCF,AF=FD,
∴△AFG≌△CFD(AAS)。∴CF=GF,AG=CD。
∵CE⊥AB,∴EF=GF。∴∠AEF=∠G。
∵AB=5,BC=10,点F是AD的中点,∴AG=5,AF=AD=BC=5。∴AG=AF。
∴∠AFG=∠G。
在△AFG中,∠EFC=∠AEF+∠G=2∠AEF,
又∵∠CFD=∠AFG,∴∠CFD=∠AEF。
∴∠EFD=∠EFC+∠CFD=2∠AEF+∠AEF=3∠AEF,
因此,存在正整数k=3,使得∠EFD=3∠AEF。
②设BE=x,∵AG=CD=AB=5,∴EG=AE+AG=5﹣x+5=10﹣x,
在Rt△BCE中,CE2=BC2﹣BE2=100﹣x2。
在Rt△CEG中,CG2=EG2+CE2=(10﹣x)2+100﹣x2=200﹣20x。
∵CF=GF(①中已证),∴CF2=(CG)2=CG2=(200﹣20x)=50﹣5x。
∴CE2﹣CF2=100﹣x2﹣50+5x=﹣x2+5x+50=﹣(x﹣)2+50+。
∴当x=,即点E是AB的中点时,CE2﹣CF2取最大值。
【例4】解:(1)HD:GC:EB=1: :1。
(2)连接AG、AC,
∵△ADC和△AHG都是等腰直角三角形,
∴AD:AC=AH:AG=1:,∠DAC=∠HAG=45°。
∴∠DAH=∠CAG。∴△DAH∽△CAG。
∴HD:GC=AD:AC=1:。
∵∠DAB=∠HAE=90°,∴∠DAH=∠BAE。
又∵AD=AB,AH=AE,∴△DAH≌△BAE(SAS)。∴HD=EB。
∴HD:GC:EB=1::1。
(3)有变化,HD:GC:EB=。
【考点】正方形的性质,等腰直角三角形的判定和性质,相似三角形的判定和性质,全等三角形的判定和性质,勾股定理。
【分析】(1)连接AG,
∵正方形AEGH的顶点E、H在正方形ABCD的边上,
∴∠GAE=∠CAB=45°,AE=AH,AB=AD。
∴A,G,C共线,AB-AE=AD-AH,∴HD=BE。
∵
∴GC=AC-AG=AB-AE= (AB-AE)= BE。
∴HD:GC:EB=1::1。
(2)连接AG、AC,由△ADC和△A ( http: / / www.21cnjy.com )HG都是等腰直角三角形,易证得△DAH∽△CAG与△DAH≌△BAE,利用相似三角形的对应边成比例与正方形的性质,即可求得HD:GC:EB的值。
(3)连接AG、AC,
∵矩形AEGH的顶点E、H在矩形ABCD的边上,
DA:AB=HA:AE=m:n,
∴∠ADC=∠AHG=90°,∴△ADC∽△AHG。
∴AD:AC=AH:AG=,∠DAC=∠HAG。
∴∠DAH=∠CAG。∴△DAH∽△CAG。
∴HD:GC=AD:AC=。
∵∠DAB=∠HAE=90°,∴∠DAH=∠BAE。
∵DA:AB=HA:AE=m:n,∴△ADH∽△ABE。∴DH:BE=AD:AB=m:n。
∴HD:GC:EB=。
【例5】解:(1)180°-2α。
(2)EB=EF。证明如下:
连接BD交EF于点O,连接BF。
∵AD∥BC,∴∠A=180°-∠ABC=180°-2α,
∠ADC=180°-∠C=180°-α。
∵AB=AD,∴∠ADB=(180°-∠A)=α。
∴∠BDC=∠ADC-∠ADB=180°-2α。
由(1)得:∠BEF=180°-2α=∠BDC。
又∵∠EOB=∠DOF,∴△EOB∽△DOF。∴,即。
∵∠EOD=∠BOF,∴△EOD∽△BOF。∴∠EFB=∠EDO=α。
∴∠EBF=180°-∠BEF-∠EFB=α=∠EFB。∴EB=EF。
(3) 延长AB至G,使AG=AE,连接BE,GE,
则∠G=∠AEG=。
∵AD∥BC,
∴∠EDF=∠C=α,∠GBC=∠A,∠DEB=∠EBC。
∴∠EDF=∠G。
∵∠BEF=∠A,∴∠BEF=∠GBC。
∴∠GBC+∠EBC=∠DEB+∠BEF,即∠EBG=∠FED。
∴△DEF∽△GBE。∴。
∵AB=mDE,AD=nDE,∴AG=AE=(n+1)DE。
∴BG=AG-AB=(n+1)DE-mDE=(n+1-m)DE。
∴。
【考点】梯形的性质,平行线的性质,相似三角形的判定和性质,等腰三角形的性质。
【分析】(1)由梯形ABCD中 ( http: / / www.21cnjy.com ),AD∥BC,∠ABC=2∠BCD=2α,根据平行线的性质,易求得∠A的度数,又由∠BEF=∠A,即可求得∠BEF的度数:
∵梯形ABCD中,AD∥BC,∴∠A+∠ABC=180°。∴∠A=180°-∠ABC=180°-2α。
又∵∠BEF=∠A,∴∠BEF=∠A=180°-2α。
(2)连接BD交EF于点O,连接BF,由AB=AD,易证得△EOB∽△DOF,根据相似三角形的对应边成比例,可得 ,从而可证得△EOD∽△BOF,又由相似三角形的对应角相等,易得∠EBF=∠EFB=α,即可得EB=EF。
(3)延长AB至G,使AG=AE,连接BE,GE,易证得△DEF∽△GBE,然后由相似三角形的对应边成比例,即可求得 的值。解析:延长DF,BA交于G,可证△CEM≌△CFM, △CDF≌△BGF,通过线段的简单运算,即可求得。
【例6】【解析】(1)根据折叠前后的相 ( http: / / www.21cnjy.com )等线段,先在Rt△OEC中求出OE长,再在Rt△ADE中运用勾股定理构建方程求AD.然后将O,D,C三点的坐标代入抛物线y=ax2+bx+c求出a,b,c即可.(2)分别用含t的代数式表示CQ和CP的长,再利用相似三角形产生的相似比构建含t的方程,解之即得.(3)从两定点C,E形成的边CE为平行四边形的边和对角线两个角度分析求解.
【答案】解:(1)∵四边形ABCO为矩形,
∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10.
由题意得,△BDC≌△EDC.
∴∠B=∠DEC=90°,EC=BC=10,ED=BD.
由勾股定理易得EO=6.
∴AE=10-6=4.
设AD=x,则BD=DE=8-x,由勾股定理,得x2+42=(8-x)2.
解之得,x=3,∴AD=3.
∵抛物线y=ax2+bx+c过点O(0,0),∴c=0.
∵抛物线y=ax2+bx+c过点D(3,10),C(8,0),
∴解之得
∴抛物线的解析式为:y=-x2+x.
(2)∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,
∴∠DEA=∠OCE.
由(1)可得AD=3,AE=4,DE=5.
而CQ=t,EP=2t,PC=10-2t.
当∠PQC=∠DAE=90°时,△ADE∽△QPC,
∴=,即=,解得t=.
当∠QPC=∠DAE=90°时,△ADE∽△PQC,
∴=,即=,解得t=.
∴当t=或时,以P,Q,C为顶点的三角形与△ADE相似.
(3)存在.M1(-4,-32),N1(4,-38).
M2(12,-32),N2(4,-26).
M3(4,),N3(4,-).
5、解:(1)∵四边形ABCD是菱形,∴△AOB为直角三角形,且OA=AC=1,OB=BD= 3。
在Rt△AOB中,由勾股定理得:AB=。
(2)①△AEF是等边三角形。理由如下:
∵由(1)知,菱形边长为2,AC=2,∴△ABC与△ACD均为等边三角形。
∴∠BAC=∠BAE+∠CAE=60°。
又∠EAF=∠CAF+∠CAE=60°,∴∠BAE=∠CAF。
在△ABE与△ACF中,∵∠BAE=∠CAF ,AB=AC=2 ,∠EBA=∠FCA=60°,
∴△ABE≌△ACF(ASA)。∴AE=AF。∴△AEF是等腰三角形。
又∵∠EAF=60°,∴△AEF是等边三角形。
②BC=2,E为四等分点,且BE>CE,∴CE=,BE=。
由①知△ABE≌△ACF,∴CF=BE=。
∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°(三角形内角和定理),
∠AEG=∠FCG=60°(等边三角形内角),∠EGA=∠CGF(对顶角),
∴∠EAC=∠GFC。
在△CAE与△CFG中,∵ ∠EAC=∠GFC ,∠ACE=∠FCG=60°,
∴△CAE∽△CFG 。∴,即。解得:CG=。
【考点】旋转的性质,菱形的性质,相似三角形的判定和性质,全等三角形的判定和性质,等边三角形的判定和性质,勾股定理。
【分析】(1)根据菱形的性质,确定△AOB为直角三角形,然后利用勾股定理求出边AB的长度。
(2)①确定一对全等三角形△ABE≌△ACF,得到AE=AF,再根据已知条件∠EAF=60°,可以判定△AEF是等边三角形。
②确定一对相似三角形△CAE∽△CFG,由对应边的比例关系求出CG的长度。
【学习目标】
1、牢记四边形的有关性质及其判定;
2、运用四边形的性质及判定进行有关计算与证明;
3、数学思想方法的合理运用。
【考点透视】
1.平行四边形的性质及判定方法。 2.矩形的性质及判定方法。
3.菱形的性质及判定方法。 4.正方形的性质及判定方法。
5.梯形的概念及判定方法。 6.梯形问题的转化。
【数学思想方法】
§Ⅰ梯形的常见辅助线的添加方法:
通过添加辅助线,把梯形转化成平行四边形和三角形.(作高、平移腰、延腰、平移对角线、等积变化)
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
§Ⅱ一招制胜——图形分离法
【精彩知识】
题型一: 选择题
【例1】如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则阴影部分的面积是( )
A. B.2 C.3 D.
★考点感悟:
●变式练习:
1、如图,菱形ABCD中,AB=2,∠A ( http: / / www.21cnjy.com )=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
A. 1 B. C. 2 D.+1
2、如图,梯形ABCD中,AB∥CD,点 ( http: / / www.21cnjy.com )E、F、G分别是BD、AC、DC的中点.已知两底差是6,两腰和是12,则△EFG的周长是( )
A.8 B.9 C.10 D.12
3、在面积为15的平行四边 ( http: / / www.21cnjy.com )形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )
A.11+ B.11-
C.11+或11- D.11-或1+
题型二:填空题
【例2】如图,菱形ABCD中,AB=A ( http: / / www.21cnjy.com )C,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH,④AD 2=OD·DH中,正确的结论是 .
●变式练习:
1. 如图,线段AC=n+1(其中 ( http: / / www.21cnjy.com )n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为Sn.当n≥2时,Sn﹣Sn﹣1= .
2、如图,在四边形ABCD中,AC=BD=6,E、F、G、H分别是AB、BC、CD、DA的中点,则EG2+FH2= 。
1题图 2题图
题型三:计算与证明
Ⅰ 常规试题
【例3】如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2﹣CF2取最大值时,求C点的位置.
★考点感悟:
Ⅱ 新型试题
【例4】(1)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD∶GC∶EB的结果(不必写计算过程);
(2)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD∶GC∶EB;
(3)把图(2)中的正方形都换成矩形,如图( ( http: / / www.21cnjy.com )3),且已知DA∶AB=HA∶AE=m: n,此时HD∶GC∶EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).
( http: / / www.21cnjy.com )
★考点感悟:
【例5】如图1,梯形ABCD中,AD∥BC,∠ABC=2∠BCD=2α,点E在AD上,点F在DC上,且∠BEF=∠A.
(1)∠BEF=_____(用含α的代数式表示);
(2)当AB=AD时,猜想线段ED、EF的数量关系,并证明你的猜想;
(3)当AB≠AD时,将“点E在AD上”改为“点E在AD的延长线上,且AE>AB,AB=mDE,AD=nDE”,其他条件不变(如图2),求的值(用含m、n的代数式表示)。
( http: / / www.21cnjy.com )
★考点感悟:
【例6】如图,在矩形OAB ( http: / / www.21cnjy.com )C中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发 ( http: / / www.21cnjy.com ),沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与△ADE相似?
(3)点N在抛物线对称轴上,点M在抛物 ( http: / / www.21cnjy.com )线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
★考点感悟:
【课后测试】
1、如图,四边形ABCD中,∠BAD= ( http: / / www.21cnjy.com )120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
A. 130° B. 120° C. 110° D. 100°
2、如图,在直角梯形ABCD中,A ( http: / / www.21cnjy.com )D//BC,∠C=90°,AD=5,BC=9, 以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )
A.10 B.11 C.12 D.13
3、如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(1)求证:△BDG∽△DEG;
(2)若EG BG=4,求BE的长.
4、如图,梯形ABCD中,AD∥BC,∠ ( http: / / www.21cnjy.com )DCB=45°,CD =2,BD⊥CD .过点C作CE⊥AB于E,对角线BD于F.点G为BC中点,连结EG、AF.
(1)求EG的长;
(2)求证:CF =AB +AF.
5、如图1,在菱形ABCD中,AC=2,BD=2 3 ,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角 ( http: / / www.21cnjy.com )板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
( http: / / www.21cnjy.com )
部分答案与提示:
【例1】如图,设BF、CE相交于点M,
∵菱形ABCD和菱形ECGF的边长分别为2和3,
∴△BCM∽△BGF,∴,即。
解得CM=1.2。∴DM=2﹣1.2=0.8。
∵∠A=120°,∴∠ABC=180°﹣120°=60°。
∴菱形ABCD边CD上的高为2sin60°=2×,
菱形ECGF边CE上的高为3sin60°=3×。
∴阴影部分面积=S△BDM+S△DFM=×0.8×+×0.8×。故选A。
【例3】解:(1)∵α=60°,BC=10,∴sinα=,即sin60°=,解得CE=。
(2)①存在k=3,使得∠EFD=k∠AEF。理由如下:
连接CF并延长交BA的延长线于点G,
∵F为AD的中点,∴AF=FD。
在平行四边形ABCD中,AB∥CD,∴∠G=∠DCF。
在△AFG和△CFD中,
∵∠G=∠DCF, ∠G=∠DCF,AF=FD,
∴△AFG≌△CFD(AAS)。∴CF=GF,AG=CD。
∵CE⊥AB,∴EF=GF。∴∠AEF=∠G。
∵AB=5,BC=10,点F是AD的中点,∴AG=5,AF=AD=BC=5。∴AG=AF。
∴∠AFG=∠G。
在△AFG中,∠EFC=∠AEF+∠G=2∠AEF,
又∵∠CFD=∠AFG,∴∠CFD=∠AEF。
∴∠EFD=∠EFC+∠CFD=2∠AEF+∠AEF=3∠AEF,
因此,存在正整数k=3,使得∠EFD=3∠AEF。
②设BE=x,∵AG=CD=AB=5,∴EG=AE+AG=5﹣x+5=10﹣x,
在Rt△BCE中,CE2=BC2﹣BE2=100﹣x2。
在Rt△CEG中,CG2=EG2+CE2=(10﹣x)2+100﹣x2=200﹣20x。
∵CF=GF(①中已证),∴CF2=(CG)2=CG2=(200﹣20x)=50﹣5x。
∴CE2﹣CF2=100﹣x2﹣50+5x=﹣x2+5x+50=﹣(x﹣)2+50+。
∴当x=,即点E是AB的中点时,CE2﹣CF2取最大值。
【例4】解:(1)HD:GC:EB=1: :1。
(2)连接AG、AC,
∵△ADC和△AHG都是等腰直角三角形,
∴AD:AC=AH:AG=1:,∠DAC=∠HAG=45°。
∴∠DAH=∠CAG。∴△DAH∽△CAG。
∴HD:GC=AD:AC=1:。
∵∠DAB=∠HAE=90°,∴∠DAH=∠BAE。
又∵AD=AB,AH=AE,∴△DAH≌△BAE(SAS)。∴HD=EB。
∴HD:GC:EB=1::1。
(3)有变化,HD:GC:EB=。
【考点】正方形的性质,等腰直角三角形的判定和性质,相似三角形的判定和性质,全等三角形的判定和性质,勾股定理。
【分析】(1)连接AG,
∵正方形AEGH的顶点E、H在正方形ABCD的边上,
∴∠GAE=∠CAB=45°,AE=AH,AB=AD。
∴A,G,C共线,AB-AE=AD-AH,∴HD=BE。
∵
∴GC=AC-AG=AB-AE= (AB-AE)= BE。
∴HD:GC:EB=1::1。
(2)连接AG、AC,由△ADC和△A ( http: / / www.21cnjy.com )HG都是等腰直角三角形,易证得△DAH∽△CAG与△DAH≌△BAE,利用相似三角形的对应边成比例与正方形的性质,即可求得HD:GC:EB的值。
(3)连接AG、AC,
∵矩形AEGH的顶点E、H在矩形ABCD的边上,
DA:AB=HA:AE=m:n,
∴∠ADC=∠AHG=90°,∴△ADC∽△AHG。
∴AD:AC=AH:AG=,∠DAC=∠HAG。
∴∠DAH=∠CAG。∴△DAH∽△CAG。
∴HD:GC=AD:AC=。
∵∠DAB=∠HAE=90°,∴∠DAH=∠BAE。
∵DA:AB=HA:AE=m:n,∴△ADH∽△ABE。∴DH:BE=AD:AB=m:n。
∴HD:GC:EB=。
【例5】解:(1)180°-2α。
(2)EB=EF。证明如下:
连接BD交EF于点O,连接BF。
∵AD∥BC,∴∠A=180°-∠ABC=180°-2α,
∠ADC=180°-∠C=180°-α。
∵AB=AD,∴∠ADB=(180°-∠A)=α。
∴∠BDC=∠ADC-∠ADB=180°-2α。
由(1)得:∠BEF=180°-2α=∠BDC。
又∵∠EOB=∠DOF,∴△EOB∽△DOF。∴,即。
∵∠EOD=∠BOF,∴△EOD∽△BOF。∴∠EFB=∠EDO=α。
∴∠EBF=180°-∠BEF-∠EFB=α=∠EFB。∴EB=EF。
(3) 延长AB至G,使AG=AE,连接BE,GE,
则∠G=∠AEG=。
∵AD∥BC,
∴∠EDF=∠C=α,∠GBC=∠A,∠DEB=∠EBC。
∴∠EDF=∠G。
∵∠BEF=∠A,∴∠BEF=∠GBC。
∴∠GBC+∠EBC=∠DEB+∠BEF,即∠EBG=∠FED。
∴△DEF∽△GBE。∴。
∵AB=mDE,AD=nDE,∴AG=AE=(n+1)DE。
∴BG=AG-AB=(n+1)DE-mDE=(n+1-m)DE。
∴。
【考点】梯形的性质,平行线的性质,相似三角形的判定和性质,等腰三角形的性质。
【分析】(1)由梯形ABCD中 ( http: / / www.21cnjy.com ),AD∥BC,∠ABC=2∠BCD=2α,根据平行线的性质,易求得∠A的度数,又由∠BEF=∠A,即可求得∠BEF的度数:
∵梯形ABCD中,AD∥BC,∴∠A+∠ABC=180°。∴∠A=180°-∠ABC=180°-2α。
又∵∠BEF=∠A,∴∠BEF=∠A=180°-2α。
(2)连接BD交EF于点O,连接BF,由AB=AD,易证得△EOB∽△DOF,根据相似三角形的对应边成比例,可得 ,从而可证得△EOD∽△BOF,又由相似三角形的对应角相等,易得∠EBF=∠EFB=α,即可得EB=EF。
(3)延长AB至G,使AG=AE,连接BE,GE,易证得△DEF∽△GBE,然后由相似三角形的对应边成比例,即可求得 的值。解析:延长DF,BA交于G,可证△CEM≌△CFM, △CDF≌△BGF,通过线段的简单运算,即可求得。
【例6】【解析】(1)根据折叠前后的相 ( http: / / www.21cnjy.com )等线段,先在Rt△OEC中求出OE长,再在Rt△ADE中运用勾股定理构建方程求AD.然后将O,D,C三点的坐标代入抛物线y=ax2+bx+c求出a,b,c即可.(2)分别用含t的代数式表示CQ和CP的长,再利用相似三角形产生的相似比构建含t的方程,解之即得.(3)从两定点C,E形成的边CE为平行四边形的边和对角线两个角度分析求解.
【答案】解:(1)∵四边形ABCO为矩形,
∴∠OAB=∠AOC=∠B=90°,AB=CO=8,AO=BC=10.
由题意得,△BDC≌△EDC.
∴∠B=∠DEC=90°,EC=BC=10,ED=BD.
由勾股定理易得EO=6.
∴AE=10-6=4.
设AD=x,则BD=DE=8-x,由勾股定理,得x2+42=(8-x)2.
解之得,x=3,∴AD=3.
∵抛物线y=ax2+bx+c过点O(0,0),∴c=0.
∵抛物线y=ax2+bx+c过点D(3,10),C(8,0),
∴解之得
∴抛物线的解析式为:y=-x2+x.
(2)∵∠DEA+∠OEC=90°,∠OCE+∠OEC=90°,
∴∠DEA=∠OCE.
由(1)可得AD=3,AE=4,DE=5.
而CQ=t,EP=2t,PC=10-2t.
当∠PQC=∠DAE=90°时,△ADE∽△QPC,
∴=,即=,解得t=.
当∠QPC=∠DAE=90°时,△ADE∽△PQC,
∴=,即=,解得t=.
∴当t=或时,以P,Q,C为顶点的三角形与△ADE相似.
(3)存在.M1(-4,-32),N1(4,-38).
M2(12,-32),N2(4,-26).
M3(4,),N3(4,-).
5、解:(1)∵四边形ABCD是菱形,∴△AOB为直角三角形,且OA=AC=1,OB=BD= 3。
在Rt△AOB中,由勾股定理得:AB=。
(2)①△AEF是等边三角形。理由如下:
∵由(1)知,菱形边长为2,AC=2,∴△ABC与△ACD均为等边三角形。
∴∠BAC=∠BAE+∠CAE=60°。
又∠EAF=∠CAF+∠CAE=60°,∴∠BAE=∠CAF。
在△ABE与△ACF中,∵∠BAE=∠CAF ,AB=AC=2 ,∠EBA=∠FCA=60°,
∴△ABE≌△ACF(ASA)。∴AE=AF。∴△AEF是等腰三角形。
又∵∠EAF=60°,∴△AEF是等边三角形。
②BC=2,E为四等分点,且BE>CE,∴CE=,BE=。
由①知△ABE≌△ACF,∴CF=BE=。
∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°(三角形内角和定理),
∠AEG=∠FCG=60°(等边三角形内角),∠EGA=∠CGF(对顶角),
∴∠EAC=∠GFC。
在△CAE与△CFG中,∵ ∠EAC=∠GFC ,∠ACE=∠FCG=60°,
∴△CAE∽△CFG 。∴,即。解得:CG=。
【考点】旋转的性质,菱形的性质,相似三角形的判定和性质,全等三角形的判定和性质,等边三角形的判定和性质,勾股定理。
【分析】(1)根据菱形的性质,确定△AOB为直角三角形,然后利用勾股定理求出边AB的长度。
(2)①确定一对全等三角形△ABE≌△ACF,得到AE=AF,再根据已知条件∠EAF=60°,可以判定△AEF是等边三角形。
②确定一对相似三角形△CAE∽△CFG,由对应边的比例关系求出CG的长度。
同课章节目录
