第六章 反比例函数 章末复习(共30张PPT)-2023-2024学年九年级数学上册同步精品课堂(北师大版)
文档属性
| 名称 | 第六章 反比例函数 章末复习(共30张PPT)-2023-2024学年九年级数学上册同步精品课堂(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 21:16:40 | ||
图片预览










文档简介
(共30张PPT)
章末讲义
第六章 反比例函数
有关概念
一般地,形如y= (k为常数,且k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.
【注意】
1)自变量x的取值范围是所有非零实数.
2)等价变形( k≠0 ):
y= y=kx-1 k=xy(x≠0) y是x的反比例函数
有关方法
利用待定系数法求反比例函数解析式的具体方法:
①设出含有待定系数的反比例函数解析式,
②将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程;
③解方程,求出待定系数;
④写出反比例函数解析式.
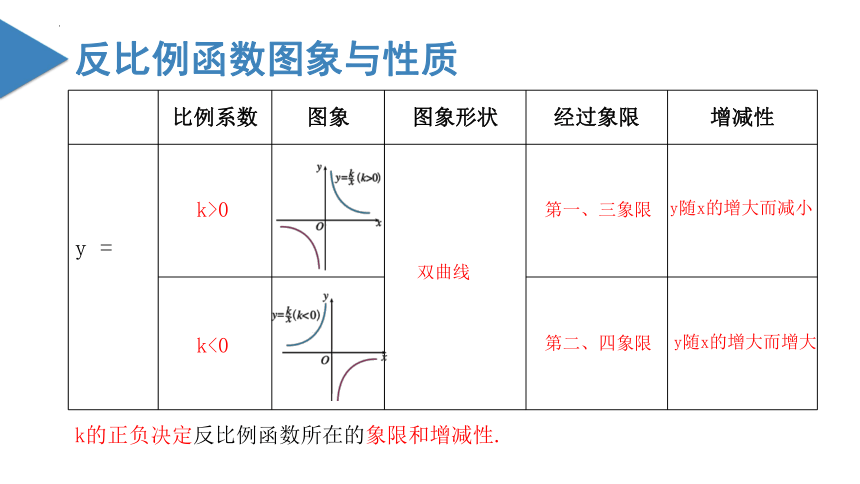
反比例函数图象与性质
比例系数 图象 图象形状 经过象限 增减性
y =
k>0
k<0
双曲线
第一、三象限
第二、四象限
y随x的增大而减小
y随x的增大而增大
k的正负决定反比例函数所在的象限和增减性.
解题技巧
在反比例函数的图象上任取一点,分别作坐标轴的垂线(或平行线),
1)与坐标轴所围成的矩形的面积S矩形= |k|.
2)与坐标轴所围成的三角形的面积S三角形= |k|.
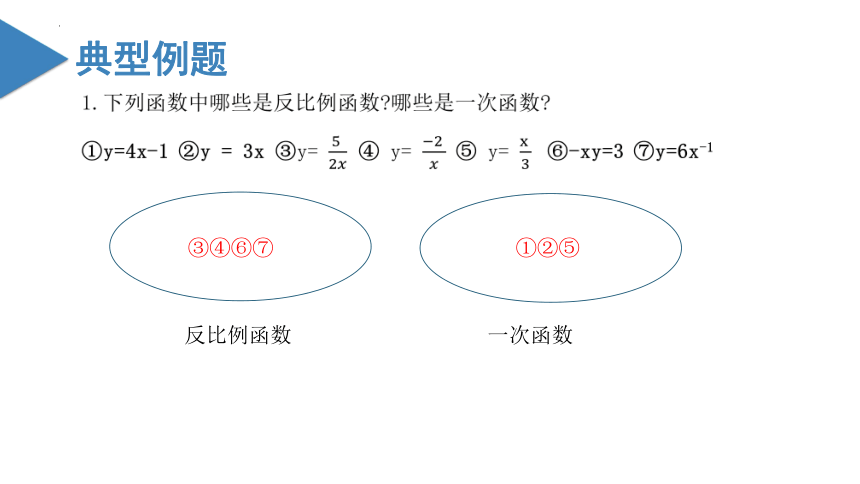
1.下列函数中哪些是反比例函数 哪些是一次函数
①y=4x-1 ②y = 3x ③y= ④ y= ⑤ y= ⑥-xy=3 ⑦y=6x-1
反比例函数
一次函数
①②⑤
③④⑥⑦
2.下列函数中,是的反比例函数的有( )个.
①;②;③;④;⑤;⑥.
A.2 B.3 C.4 D.5
1.如果函数反比例函数,那么的值是( )
A.2 B.-1 C.1 D.0
2.当m取何值时,是关于x的反比例函数?
【详解】∵是关于x的反比例函数,
∴,解得,
∴,
3. 已知是关于的反比例函数,则( )
A. B. C. D.为一切实数
4. 若函数y=(m﹣1)x|m|﹣2是反比例函数,则m的值是( )
A.m=﹣1 B.m=1
C.m=﹣1或m=1 D.m=﹣2或m=2
【详解】解:由题意得:,解得m=-1,故选:A.
解由题意得: 解得
(2)∵反比例函数 当
∴点不在这个函数图象上.
5.函数y=(m﹣1)是反比例函数
1)求m的值
2)判断点(,2)是否在这个函数的图象上.
1.已知反比例函数,则它的图象经过点( )
A. B. C. D.
2.下列四个点,在反比例函数图象上的是( )
A. B. C. D.
1. 若反比例函数y= 的图象经过点(2,-1),则该反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
2.已知函数是反比例函数,则此反比例函数的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、四象限 D.第二、三象限
【详解】根据已知条件,得即
∴函数解析式为
∴此反比例函数的图象在第一、三象限,故答案为A.
3. 已知反比例函数的图象经过点,则这个函数的图象位于( )
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
1.比例函数的图象在二、四象限,则的值可以是( )
A.-1 B.2 C.1 D.0
2.如果反比例函数(a是常数)的图象在第一、三象限,那么a的取值范围是( )
A.a<0 B.a>0 C.a<2 D.a>2
1.若反比例函数y=的图象在其所在的每一象限内,y随x的增大而减小,则k的取值范围是( )
A.k<-2 B.k>-2 C.k<2 D.k>2
2.反比例函数的图象,当x>0时,y随x的值增大而增大,则k的取值范围是( )
A.k<2 B.k≤2 C.k>2 D.k≥2
1.反比例函数y=- 的图象大致是( )
y
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
1.反比例函数y= 的图象大致是( )
y
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
1. 在同一平面直角坐标系中,函数()与的图象可能是( )
2.(2020·青海·中考真题)若,则正比例函数=y=ax与反比例函数在同一平面直角坐标系中的大致图像可能是( )
1.如图,两个反比例函数y和y在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
A.1 B.2 C.4 D.无法计算
【详解】∵PA⊥x轴于点A,交C2于点B,
∴S△POA4=2,S△BOA2=1,
∴S△POB=2﹣1=1.故选:A.
求阴影部分面积的方法:
当它无法直接求出时,一般都采用“转化”的方法,将它转化为易求图形面积的和或差来进行计算.如本例就是将阴影部分面积转化为两个与比例系数相关的特殊三角形的面积的差来求,要注意转化思想和作差法的运用.
2.如图,在函数(x>0)的图象上有三点A,B,C过这三点分别向x轴、y 轴作垂线,过每一点所作的两条垂线与x轴、 y轴围成的矩形的面积分别为SA ,SB,SC,则 ( )
A. SA >SB>SC B. SAC. SA =SB=SC D. SAC
3. 如图,A、B两点在双曲线y= 上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )
A.3 B.4 C.5 D.6
【详解】∵点A、B是双曲线y= 上的点,分别经过A、B两点向x轴、y轴作垂线段,
则根据反比例函数的图象的性质得两个矩形的面积都等于|k|=4,
∴S1+S2=4+4-1×2=6.故选D.
1.如图所示,P是反比例函数y=的图象上一点,过点P作 PB⊥x 轴于点B,点A在y轴上,△ABP的面积为 2,则k的值为___________
O
B
A
P
x
y
4
2.如图,直y=mx与双曲线交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是( )
A.1 B.m﹣1 C.2 D.m
【详解】解:由图象上的点A、B、M构成的三角形由△AMO和△BMO的组成,
点A与点B关于原点中心对称,
∴点A,B的纵横坐标的绝对值相等,
∴△AMO和△BMO的面积相等,且为,
∴点A的横纵坐标的乘积绝对值为1,
又因为点A在第一象限内,
所以可知反比例函数的系数k为1.
故选A.
1.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当R=6Ω时,
2.古希腊学者阿基米德发现了著名的“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂.几位同学玩撬石头游戏,已知阻力(石头重量)和阻力臂分别为1600N和0.5m,小明最多能使出500N的力量,若要撬动这块大石头,他该选择撬棍的动力臂( )
A.至多为 B.至少为 C.至多为 D.至少为
【详解】解:由题意可得:1600×0.5=Fl,则F与l的函数表达式为:F=;
当动力F=500N时,500=,解得l==1.6,
故选:B.
3.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图像,其中BC段是双曲线(k≠0)的一部分,则当x = 16时,大棚内的温度约为( )
A.18℃ B.15.5℃ C.13.5℃ D.12℃
【详解】解:∵点B(12,18)在双曲线上,∴,
解得:k=216.当x=16时,y==13.5,
所以当x=16时,大棚内的温度约为13.5℃.故选:C.
4.青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差 小时.
【详解】解:设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,
把点代入得:,解得:,
∴设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,
当时,(小时),
当时,(小时),
(小时),
故答案为:.
5.如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的总蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
(1)设V=.∵点(12,4000)在此函数图象上,∴蓄水量为12×4000=48000m3;
(2)∵点(12,4000)在此函数图象上,∴4000=,k=48000,
∴此函数的解析式V=;
(3)∵当t=6时,V==8000m3;∴每小时的排水量应该是8000m3.
6.我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
(1)把B(12,20)代入中得:k=12×20=240;
(2)设AD的解析式为:y=mx+n.把(0,10)、(2,20)代入y=mx+n中得:
,解得:,
∴AD的解析式为:y=5x+10.当y=15时,15=5x+10,x=1,15=,x==16,∴16﹣1=15.
答:恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有15小时.
章末讲义
第六章 反比例函数
有关概念
一般地,形如y= (k为常数,且k≠0)的函数,叫做反比例函数,其中x是自变量,y是函数.
【注意】
1)自变量x的取值范围是所有非零实数.
2)等价变形( k≠0 ):
y= y=kx-1 k=xy(x≠0) y是x的反比例函数
有关方法
利用待定系数法求反比例函数解析式的具体方法:
①设出含有待定系数的反比例函数解析式,
②将已知条件(自变量与函数的对应值)代入解析式,得到关于待定系数的方程;
③解方程,求出待定系数;
④写出反比例函数解析式.
反比例函数图象与性质
比例系数 图象 图象形状 经过象限 增减性
y =
k>0
k<0
双曲线
第一、三象限
第二、四象限
y随x的增大而减小
y随x的增大而增大
k的正负决定反比例函数所在的象限和增减性.
解题技巧
在反比例函数的图象上任取一点,分别作坐标轴的垂线(或平行线),
1)与坐标轴所围成的矩形的面积S矩形= |k|.
2)与坐标轴所围成的三角形的面积S三角形= |k|.
1.下列函数中哪些是反比例函数 哪些是一次函数
①y=4x-1 ②y = 3x ③y= ④ y= ⑤ y= ⑥-xy=3 ⑦y=6x-1
反比例函数
一次函数
①②⑤
③④⑥⑦
2.下列函数中,是的反比例函数的有( )个.
①;②;③;④;⑤;⑥.
A.2 B.3 C.4 D.5
1.如果函数反比例函数,那么的值是( )
A.2 B.-1 C.1 D.0
2.当m取何值时,是关于x的反比例函数?
【详解】∵是关于x的反比例函数,
∴,解得,
∴,
3. 已知是关于的反比例函数,则( )
A. B. C. D.为一切实数
4. 若函数y=(m﹣1)x|m|﹣2是反比例函数,则m的值是( )
A.m=﹣1 B.m=1
C.m=﹣1或m=1 D.m=﹣2或m=2
【详解】解:由题意得:,解得m=-1,故选:A.
解由题意得: 解得
(2)∵反比例函数 当
∴点不在这个函数图象上.
5.函数y=(m﹣1)是反比例函数
1)求m的值
2)判断点(,2)是否在这个函数的图象上.
1.已知反比例函数,则它的图象经过点( )
A. B. C. D.
2.下列四个点,在反比例函数图象上的是( )
A. B. C. D.
1. 若反比例函数y= 的图象经过点(2,-1),则该反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、三象限 D.第二、四象限
2.已知函数是反比例函数,则此反比例函数的图象在( )
A.第一、三象限 B.第二、四象限
C.第一、四象限 D.第二、三象限
【详解】根据已知条件,得即
∴函数解析式为
∴此反比例函数的图象在第一、三象限,故答案为A.
3. 已知反比例函数的图象经过点,则这个函数的图象位于( )
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
1.比例函数的图象在二、四象限,则的值可以是( )
A.-1 B.2 C.1 D.0
2.如果反比例函数(a是常数)的图象在第一、三象限,那么a的取值范围是( )
A.a<0 B.a>0 C.a<2 D.a>2
1.若反比例函数y=的图象在其所在的每一象限内,y随x的增大而减小,则k的取值范围是( )
A.k<-2 B.k>-2 C.k<2 D.k>2
2.反比例函数的图象,当x>0时,y随x的值增大而增大,则k的取值范围是( )
A.k<2 B.k≤2 C.k>2 D.k≥2
1.反比例函数y=- 的图象大致是( )
y
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
1.反比例函数y= 的图象大致是( )
y
A.
x
y
o
B.
x
o
D.
x
y
o
C.
x
y
o
1. 在同一平面直角坐标系中,函数()与的图象可能是( )
2.(2020·青海·中考真题)若,则正比例函数=y=ax与反比例函数在同一平面直角坐标系中的大致图像可能是( )
1.如图,两个反比例函数y和y在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为( )
A.1 B.2 C.4 D.无法计算
【详解】∵PA⊥x轴于点A,交C2于点B,
∴S△POA4=2,S△BOA2=1,
∴S△POB=2﹣1=1.故选:A.
求阴影部分面积的方法:
当它无法直接求出时,一般都采用“转化”的方法,将它转化为易求图形面积的和或差来进行计算.如本例就是将阴影部分面积转化为两个与比例系数相关的特殊三角形的面积的差来求,要注意转化思想和作差法的运用.
2.如图,在函数(x>0)的图象上有三点A,B,C过这三点分别向x轴、y 轴作垂线,过每一点所作的两条垂线与x轴、 y轴围成的矩形的面积分别为SA ,SB,SC,则 ( )
A. SA >SB>SC B. SA
3. 如图,A、B两点在双曲线y= 上,分别经过A、B两点向轴作垂线段,已知S阴影=1,则S1+S2=( )
A.3 B.4 C.5 D.6
【详解】∵点A、B是双曲线y= 上的点,分别经过A、B两点向x轴、y轴作垂线段,
则根据反比例函数的图象的性质得两个矩形的面积都等于|k|=4,
∴S1+S2=4+4-1×2=6.故选D.
1.如图所示,P是反比例函数y=的图象上一点,过点P作 PB⊥x 轴于点B,点A在y轴上,△ABP的面积为 2,则k的值为___________
O
B
A
P
x
y
4
2.如图,直y=mx与双曲线交于点A,B.过点A作AM⊥x轴,垂足为点M,连接BM.若S△ABM=1,则k的值是( )
A.1 B.m﹣1 C.2 D.m
【详解】解:由图象上的点A、B、M构成的三角形由△AMO和△BMO的组成,
点A与点B关于原点中心对称,
∴点A,B的纵横坐标的绝对值相等,
∴△AMO和△BMO的面积相等,且为,
∴点A的横纵坐标的乘积绝对值为1,
又因为点A在第一象限内,
所以可知反比例函数的系数k为1.
故选A.
1.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:)是反比例函数关系,它的图象如图所示.下列说法正确的是( )
A.函数解析式为 B.蓄电池的电压是18V
C.当时, D.当R=6Ω时,
2.古希腊学者阿基米德发现了著名的“杠杆原理”:杠杆平衡时,阻力×阻力臂=动力×动力臂.几位同学玩撬石头游戏,已知阻力(石头重量)和阻力臂分别为1600N和0.5m,小明最多能使出500N的力量,若要撬动这块大石头,他该选择撬棍的动力臂( )
A.至多为 B.至少为 C.至多为 D.至少为
【详解】解:由题意可得:1600×0.5=Fl,则F与l的函数表达式为:F=;
当动力F=500N时,500=,解得l==1.6,
故选:B.
3.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图像,其中BC段是双曲线(k≠0)的一部分,则当x = 16时,大棚内的温度约为( )
A.18℃ B.15.5℃ C.13.5℃ D.12℃
【详解】解:∵点B(12,18)在双曲线上,∴,
解得:k=216.当x=16时,y==13.5,
所以当x=16时,大棚内的温度约为13.5℃.故选:C.
4.青藏铁路是当今世界上海拔最高、线路最长的高原铁路,因路况、季节、天气等原因行车的平均速度在(千米/小时)之间变化,铁路运行全程所需要的时间(小时)与运行的平均速度(千米/小时)满足如图所示的函数关系,列车运行的平均速度最大和列车运行的平均速度最小时全程所用时间相差 小时.
【详解】解:设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,
把点代入得:,解得:,
∴设铁路运行全程所需要的时间与运行的平均速度之间的表达式为,
当时,(小时),
当时,(小时),
(小时),
故答案为:.
5.如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
(1)请你根据图象提供的信息求出此蓄水池的总蓄水量;
(2)写出此函数的解析式;
(3)若要6 h排完水池中的水,那么每小时的排水量应该是多少?
(1)设V=.∵点(12,4000)在此函数图象上,∴蓄水量为12×4000=48000m3;
(2)∵点(12,4000)在此函数图象上,∴4000=,k=48000,
∴此函数的解析式V=;
(3)∵当t=6时,V==8000m3;∴每小时的排水量应该是8000m3.
6.我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?
(1)把B(12,20)代入中得:k=12×20=240;
(2)设AD的解析式为:y=mx+n.把(0,10)、(2,20)代入y=mx+n中得:
,解得:,
∴AD的解析式为:y=5x+10.当y=15时,15=5x+10,x=1,15=,x==16,∴16﹣1=15.
答:恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有15小时.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
