4.3 实数(第2课时) 课件(共28张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版)
文档属性
| 名称 | 4.3 实数(第2课时) 课件(共28张PPT)-2023-2024学年八年级数学上册同步精品课堂(苏科版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 21:17:43 | ||
图片预览








文档简介
第4章 · 平方根
4.3 实数(2)
第2课时 实数的运算
学习目标
1. 会在实数范围内求绝对值、相反数、与倒数;
2. 能熟练进行实数的运算;
3. 能用不同方法比较实数大小,理解估算的意义.
知识回顾
把下列各数填入相应的圈内:
3.1415926?,????????,?????????????,0.2121121112?,????????,0.030303?,?????????,???????????????? .
?
有理数
无理数
?
?
?
?
先化简,后判断
3.1415926?,
?
????????,
?
?????????????,
?
0.2121121112?,
?
????????,
?
0.030303?,
?
?????????
?
????????????????
?
知识回顾
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名 称
定 义
性 质
求 法
绝对值
相反数
倒 数
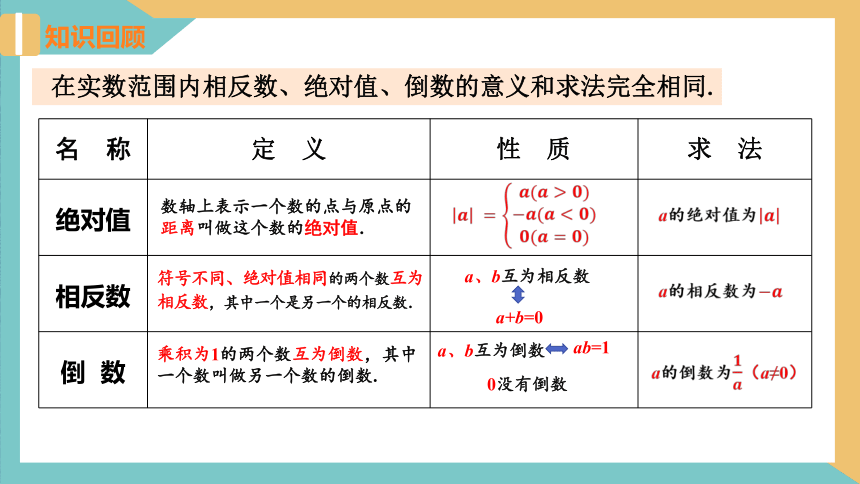
数轴上表示一个数的点与原点的距离叫做这个数的绝对值.
?????=????(????>????)?????(?????
a的绝对值为????
?
在有理数范围内,绝对值、相反数、倒数的意义是什么?
符号不同、绝对值相同的两个数互为相反数,其中一个是另一个的相反数.
a、b互为相反数
a+b=0
a的相反数为?????
?
乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数.
a、b互为倒数
ab=1
0没有倒数
a的倒数为????????(a≠0)
?
在实数范围内相反数、绝对值、倒数的意义和求法完全相同.
例1 求下列各数的相反数、倒数和绝对值.
(1)??????; (2) ????????; (3)????????; (4)?????????
?
例题讲解
解:(1)?????的相反数是????,倒数是?????????,绝对值是????.
(2) ????????的相反数是?????????,倒数是?????????,绝对值是?????????.
(3)∵????????=2,∴????????的相反数是-2,倒数是????????,绝对值是2.
(4)?????????的相反数是?(?????????)=?????????,倒数是?????????????,绝对值是?????????.
?
对于和、差形式的实数,写它的相反数时,要先添加括号,再在括号前面添加负号.
例2 计算下列各题:
例题讲解
(1) ?????(??????????)????+?????????;
?
(????)原式=?????????+????????
=????????????;
?
解:
(????)|??????????|?(?????)????????????????+????????.
?
(????)原式=???????????????+????
=?????.?
?
在实数范围内运算性质及运算律仍然适用.
例题讲解
例3 用计算器计算:
(1)????+π;
?
(2)3×??????????????;
?
(3)????????+?????(????+????????).
?
无理数与无理数的和、差、积、商不都是无理数.
无理数与有理数的积、商也不都是无理数.
讨论与交流
先通过估算比较下列各数的大小,再通过计算器验证.
(1)????与2.5;
?
(2) ?????????????与0.5.
?
小组讨论是否有其它的比较方法.
方法1:∵(????)2=5,2.52=6.25,5<6.25,
?
若a>0,b>0,且a2>b2,则a>b
?
∴????<2.5.
?
方法2:∵2.32=5.29,
∴????<2.3<2.5.
?
方法3:在数轴是表示????、2.5的电的位置,比较大小.
?
讨论与交流
(1)????与2.5;
?
(2) ?????????????与0.5.
?
解:∵0.5=????????=????????-????????,?????????????=????????-????????,且????????>????????,
∴????????-????????>????????-????????.
∴?????????????>0.5.
?
讨论与交流
方法总结
比较两个数大小的常用方法:
(1)作差比较法:若a-b>0,则a>b;若a-b=0,则a=b;若a-b<0,则a(2)作商比较法:对于两个正数a、b,若????????=1,则a=b;若????????>1,则a>b;若????????<1,则a(3)被开方数比较法:若两个数的被开方数相同,通过被开方数比较实数的大小.
(4)估算比较法:取近似值来比较.
(5)媒介比较法:若a<b,b<c,则a<c;
(6)比较两数的平方或立方.
(7)数轴比较法.
?
1.比较????与????的大小.
?
解:方法1:通过估算,比较大小:
方法2: ∵(????)2=3,(????)2=7,3<7,
?
∵?????<2,????>2,
?
∴????<????.
?
∴????<????.
?
方法3:利用数轴比较大小.
新知巩固
2.比较3与????的大小.
?
解:方法1: ∵32=9,(????)2=7,9>7,
?
∴????>????.
?
方法2: ∵3= ?????,9>7,
?
∴????>????.
?
即????>????.
?
新知巩固
3.比较????????、????、2的大小.
?
解:∵?????????<????????<????????,
?
∴????<????????<????,
?
∵?????<????<????,
?
∴ ????<????<????,
?
∴????????<????<????.
?
新知巩固
新知巩固
4.比较?????????与?????.????????????????的大小.
?
????????输入时依次按键:
?
9
2ndF
3
=
第二功能键
方根运算键
注意:利用计算器先求出两个无理数的近似值,再比较大小,这也是比较两个无理数大小的一种方法.
拓展延伸
例4 下列整数中,与??????????????????最接近的是(?? ??)
A. ???? B. ???? C. ???? D. ????
?
解:∵????????∴????∴?????∴????故选:????.
?
C
拓展延伸
变式1:估计 ?????????+1的值在(??? ?)
?
A. 2和3之间 B. 3和4之间 C. 4和5之间 D. 5和6之间
解:∵????????=????,????????=????????,所以????∴?????
C
变式2:已知x是整数,当|x-30|取最小值时,x的值是_____.
解:∵?????????∴????∵????.????????=????????.????????,
∴?????????∴与?????????最接近的整数是????,
∴当|??????????????|取最小值时,????的值是????.
?
5
拓展延伸
变式3:已知??????????????的整数????,小数部分????,则?????????????=_________.
?
解:∵?????∴?????∴?????????∴????=????,????=???????????????????=??????????????.
∴?????????????=????×?????(??????????????)=?????????+?????????
=?????????.
?
???????
?
课堂小结
实数运算
在实数范围内求绝对值、相反数、与倒数
实数的加、减、乘、除、乘方、开方运算
用不同方法比较实数大小
1.下列实数中,最大的实数是 ( )
A. -π B. -2 C.?????? D. -1
?
当堂检测
D
3.估计????+1的值在 ( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
?
2.下列无理数,与????最接近的是(?? ??)
A. ???? B. ???? C. ???????? D. ????????
?
C
A
当堂检测
4.下列各式正确的是( )
A. ?????????=±9 B. |3.14-π|=π-3.14
C. (????????)3=???? D. ?????- ?????= ????
?
B
5.下列各组数中,互为相反数的一组是( )
A.-|-2|与?????????? B.-4与-(?????)?????
C.-????????与????????? D.-2与-(?????)????
?
C
当堂检测
6.已知????+?????????的小数部分为????,??????????????的小数部分为????,则????+????= ______ .
?
1
7.定义新运算“☆”:????☆????=?????????+????,则????☆(????☆????)=______.
?
解:∵????☆????=?????×????+????=?????????=????;
∴????☆(????☆????)=????☆????=?????×????+????=????.
?
3
当堂检测
8.求下列各数的相反数、倒数和绝对值:
(1)-????????;(2)????????;(3)0.16.
?
解:(1)-????????的相反数是????????,倒数是-????????,绝对值是????????.
(2)????????的相反数是-4,倒数是????????,绝对值是4.
(3)0.16的相反数是-0.16,倒数是????????????,绝对值是0.16.
?
当堂检测
9. 比较下列各组数的大小:
(????)?????????与?????????;
?
解:(????)∵(?????????)????=????????,
(?????????)????=????????,
而????????>????????,
∴?????????>?????????;
?
(????)∵(??????????)????=????,
??????????=????,
而????>????,
即???????????
(????)??????????与??????;
?
当堂检测
9. 比较下列各组数的大小:
(????)?????与?????+?????;
?
(????)∵(?????)????=????,
(?????+?????)????=????+?????????,
而????∴??????
(????)∵????∴????∴????.????∴??????????????>????.????.?
?
(????)??????????????与????.????.
?
当堂检测
(2) (?????)????+?????????+|1?????|.
?
10.计算:
原式=3-2-(1-????)=????.
?
(1)(-10)×(??????????)-?????????+20220;
?
解:原式=5-4+1=2.
(????)(?????????)????+(?????????)?????+|??????????????|??????????.
?
原式=?????????+????????????????????????
=?????+?????.?
?
当堂检测
11.实数????,????互为相反数,????,????互为倒数,????的绝对值为????,求代数式?????????+?????+????+?????????????????????????的值.
?
解:由题意知????+????=????,??????=????,????=±????,
原式=?(±????)????+?????+?????????????????×????
=????+?????????
=????.?
?
当堂检测
12.如图,一只蚂蚁从点????沿数轴向右直爬????个单位到达点????,点????表示??????,设点????所表示的数为????.
(????)求????的值;
(????)求|?????????|+(?????????)????的值.
?
解:(????)由题意可得????=??????????;
?
(????)∵????=??????????,
∴|?????????|+(?????????)????=|???????????????|+(???????????????)????
=|??????????|+(??????)????
=??????????+????
=?????+????.
4.3 实数(2)
第2课时 实数的运算
学习目标
1. 会在实数范围内求绝对值、相反数、与倒数;
2. 能熟练进行实数的运算;
3. 能用不同方法比较实数大小,理解估算的意义.
知识回顾
把下列各数填入相应的圈内:
3.1415926?,????????,?????????????,0.2121121112?,????????,0.030303?,?????????,???????????????? .
?
有理数
无理数
?
?
?
?
先化简,后判断
3.1415926?,
?
????????,
?
?????????????,
?
0.2121121112?,
?
????????,
?
0.030303?,
?
?????????
?
????????????????
?
知识回顾
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}名 称
定 义
性 质
求 法
绝对值
相反数
倒 数
数轴上表示一个数的点与原点的距离叫做这个数的绝对值.
?????=????(????>????)?????(?????
a的绝对值为????
?
在有理数范围内,绝对值、相反数、倒数的意义是什么?
符号不同、绝对值相同的两个数互为相反数,其中一个是另一个的相反数.
a、b互为相反数
a+b=0
a的相反数为?????
?
乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数.
a、b互为倒数
ab=1
0没有倒数
a的倒数为????????(a≠0)
?
在实数范围内相反数、绝对值、倒数的意义和求法完全相同.
例1 求下列各数的相反数、倒数和绝对值.
(1)??????; (2) ????????; (3)????????; (4)?????????
?
例题讲解
解:(1)?????的相反数是????,倒数是?????????,绝对值是????.
(2) ????????的相反数是?????????,倒数是?????????,绝对值是?????????.
(3)∵????????=2,∴????????的相反数是-2,倒数是????????,绝对值是2.
(4)?????????的相反数是?(?????????)=?????????,倒数是?????????????,绝对值是?????????.
?
对于和、差形式的实数,写它的相反数时,要先添加括号,再在括号前面添加负号.
例2 计算下列各题:
例题讲解
(1) ?????(??????????)????+?????????;
?
(????)原式=?????????+????????
=????????????;
?
解:
(????)|??????????|?(?????)????????????????+????????.
?
(????)原式=???????????????+????
=?????.?
?
在实数范围内运算性质及运算律仍然适用.
例题讲解
例3 用计算器计算:
(1)????+π;
?
(2)3×??????????????;
?
(3)????????+?????(????+????????).
?
无理数与无理数的和、差、积、商不都是无理数.
无理数与有理数的积、商也不都是无理数.
讨论与交流
先通过估算比较下列各数的大小,再通过计算器验证.
(1)????与2.5;
?
(2) ?????????????与0.5.
?
小组讨论是否有其它的比较方法.
方法1:∵(????)2=5,2.52=6.25,5<6.25,
?
若a>0,b>0,且a2>b2,则a>b
?
∴????<2.5.
?
方法2:∵2.32=5.29,
∴????<2.3<2.5.
?
方法3:在数轴是表示????、2.5的电的位置,比较大小.
?
讨论与交流
(1)????与2.5;
?
(2) ?????????????与0.5.
?
解:∵0.5=????????=????????-????????,?????????????=????????-????????,且????????>????????,
∴????????-????????>????????-????????.
∴?????????????>0.5.
?
讨论与交流
方法总结
比较两个数大小的常用方法:
(1)作差比较法:若a-b>0,则a>b;若a-b=0,则a=b;若a-b<0,则a
(4)估算比较法:取近似值来比较.
(5)媒介比较法:若a<b,b<c,则a<c;
(6)比较两数的平方或立方.
(7)数轴比较法.
?
1.比较????与????的大小.
?
解:方法1:通过估算,比较大小:
方法2: ∵(????)2=3,(????)2=7,3<7,
?
∵?????<2,????>2,
?
∴????<????.
?
∴????<????.
?
方法3:利用数轴比较大小.
新知巩固
2.比较3与????的大小.
?
解:方法1: ∵32=9,(????)2=7,9>7,
?
∴????>????.
?
方法2: ∵3= ?????,9>7,
?
∴????>????.
?
即????>????.
?
新知巩固
3.比较????????、????、2的大小.
?
解:∵?????????<????????<????????,
?
∴????<????????<????,
?
∵?????<????<????,
?
∴ ????<????<????,
?
∴????????<????<????.
?
新知巩固
新知巩固
4.比较?????????与?????.????????????????的大小.
?
????????输入时依次按键:
?
9
2ndF
3
=
第二功能键
方根运算键
注意:利用计算器先求出两个无理数的近似值,再比较大小,这也是比较两个无理数大小的一种方法.
拓展延伸
例4 下列整数中,与??????????????????最接近的是(?? ??)
A. ???? B. ???? C. ???? D. ????
?
解:∵????????∴????∴?????∴????故选:????.
?
C
拓展延伸
变式1:估计 ?????????+1的值在(??? ?)
?
A. 2和3之间 B. 3和4之间 C. 4和5之间 D. 5和6之间
解:∵????????=????,????????=????????,所以????∴?????
C
变式2:已知x是整数,当|x-30|取最小值时,x的值是_____.
解:∵?????????∴????∵????.????????=????????.????????,
∴?????????∴与?????????最接近的整数是????,
∴当|??????????????|取最小值时,????的值是????.
?
5
拓展延伸
变式3:已知??????????????的整数????,小数部分????,则?????????????=_________.
?
解:∵?????∴?????∴?????????∴????=????,????=???????????????????=??????????????.
∴?????????????=????×?????(??????????????)=?????????+?????????
=?????????.
?
???????
?
课堂小结
实数运算
在实数范围内求绝对值、相反数、与倒数
实数的加、减、乘、除、乘方、开方运算
用不同方法比较实数大小
1.下列实数中,最大的实数是 ( )
A. -π B. -2 C.?????? D. -1
?
当堂检测
D
3.估计????+1的值在 ( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
?
2.下列无理数,与????最接近的是(?? ??)
A. ???? B. ???? C. ???????? D. ????????
?
C
A
当堂检测
4.下列各式正确的是( )
A. ?????????=±9 B. |3.14-π|=π-3.14
C. (????????)3=???? D. ?????- ?????= ????
?
B
5.下列各组数中,互为相反数的一组是( )
A.-|-2|与?????????? B.-4与-(?????)?????
C.-????????与????????? D.-2与-(?????)????
?
C
当堂检测
6.已知????+?????????的小数部分为????,??????????????的小数部分为????,则????+????= ______ .
?
1
7.定义新运算“☆”:????☆????=?????????+????,则????☆(????☆????)=______.
?
解:∵????☆????=?????×????+????=?????????=????;
∴????☆(????☆????)=????☆????=?????×????+????=????.
?
3
当堂检测
8.求下列各数的相反数、倒数和绝对值:
(1)-????????;(2)????????;(3)0.16.
?
解:(1)-????????的相反数是????????,倒数是-????????,绝对值是????????.
(2)????????的相反数是-4,倒数是????????,绝对值是4.
(3)0.16的相反数是-0.16,倒数是????????????,绝对值是0.16.
?
当堂检测
9. 比较下列各组数的大小:
(????)?????????与?????????;
?
解:(????)∵(?????????)????=????????,
(?????????)????=????????,
而????????>????????,
∴?????????>?????????;
?
(????)∵(??????????)????=????,
??????????=????,
而????>????,
即???????????
(????)??????????与??????;
?
当堂检测
9. 比较下列各组数的大小:
(????)?????与?????+?????;
?
(????)∵(?????)????=????,
(?????+?????)????=????+?????????,
而????∴??????
(????)∵????∴????∴????.????∴??????????????>????.????.?
?
(????)??????????????与????.????.
?
当堂检测
(2) (?????)????+?????????+|1?????|.
?
10.计算:
原式=3-2-(1-????)=????.
?
(1)(-10)×(??????????)-?????????+20220;
?
解:原式=5-4+1=2.
(????)(?????????)????+(?????????)?????+|??????????????|??????????.
?
原式=?????????+????????????????????????
=?????+?????.?
?
当堂检测
11.实数????,????互为相反数,????,????互为倒数,????的绝对值为????,求代数式?????????+?????+????+?????????????????????????的值.
?
解:由题意知????+????=????,??????=????,????=±????,
原式=?(±????)????+?????+?????????????????×????
=????+?????????
=????.?
?
当堂检测
12.如图,一只蚂蚁从点????沿数轴向右直爬????个单位到达点????,点????表示??????,设点????所表示的数为????.
(????)求????的值;
(????)求|?????????|+(?????????)????的值.
?
解:(????)由题意可得????=??????????;
?
(????)∵????=??????????,
∴|?????????|+(?????????)????=|???????????????|+(???????????????)????
=|??????????|+(??????)????
=??????????+????
=?????+????.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
