第二十二章二次函数 单元练习(含答案) 2023-—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十二章二次函数 单元练习(含答案) 2023-—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 372.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-02 22:43:07 | ||
图片预览

文档简介
第二十二章二次函数 单元练习 2023-2024学年人教版数学九年级上册
姓名 班级 学号 成绩
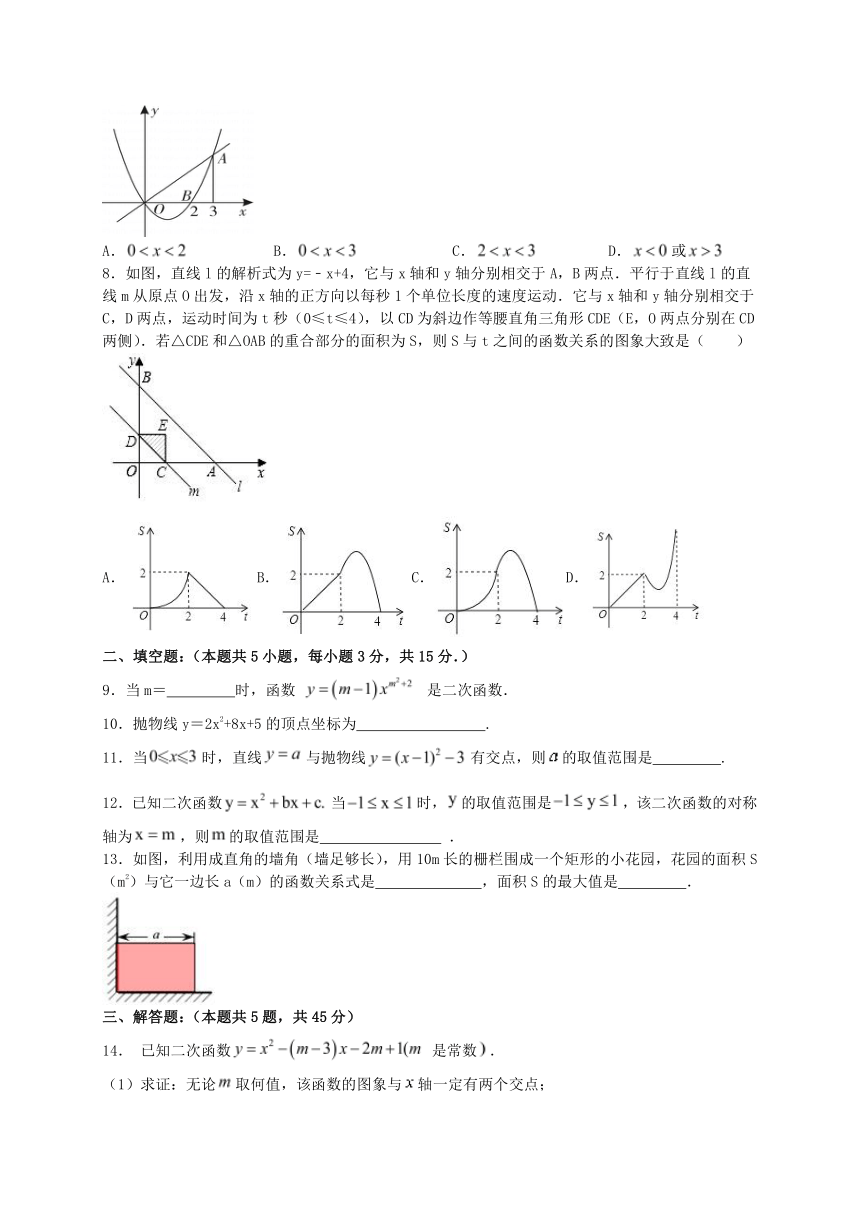
一、选择题:(本题共8小题,每小题5分,共40分.)
1.将方程转化为的形式,则的值为( )
A. B. C. D.
2.将抛物线的图象向右平移个单位,再向下平移个单位,所得图象的解析式为,则( )
A. B. C. D.
3.如图在同一个坐标系中函数和的图象可能的是( )
A.B.C.D.
4.若点,点,点在二次函数的图象上,则,,的大小关系是( )
A. B. C. D.
5.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1 B. 1.5 C.2 D.3
6.抛物线(其中,是常数)过点,且抛物线的对称轴与线段有交点,点的坐标为,点的坐标为,则的值不可能是( ).
A.9 B.11 C.13 D.15
7.如图所示,已知二次函数的图象与正比例函数的图象交于点,与轴交于点.若,则的取值范围是( ).
A. B. C. D.或
8.如图,直线l的解析式为y=﹣x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是( )
A.B.C.D.
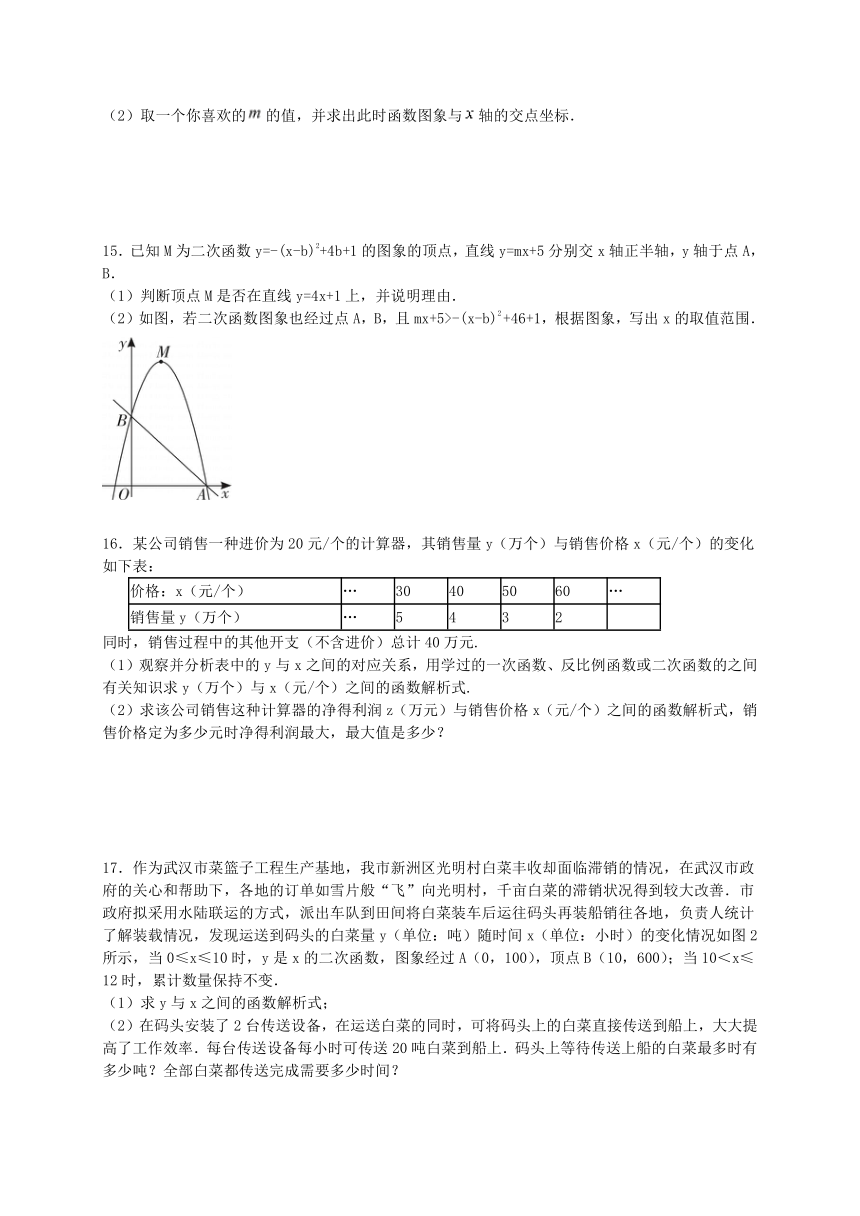
二、填空题:(本题共5小题,每小题3分,共15分.)
9.当m= 时,函数 是二次函数.
10.抛物线y=2x2+8x+5的顶点坐标为 .
11.当时,直线与抛物线有交点,则的取值范围是 .
12.已知二次函数当时,的取值范围是,该二次函数的对称轴为,则的取值范围是 .
13.如图,利用成直角的墙角(墙足够长),用10m长的栅栏围成一个矩形的小花园,花园的面积S(m2)与它一边长a(m)的函数关系式是 ,面积S的最大值是 .
三、解答题:(本题共5题,共45分)
14. 已知二次函数是常数.
(1)求证:无论取何值,该函数的图象与轴一定有两个交点;
(2)取一个你喜欢的的值,并求出此时函数图象与轴的交点坐标.
15.已知M为二次函数y=-(x-b)2+4b+1的图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
(1)判断顶点M是否在直线y=4x+1上,并说明理由.
(2)如图,若二次函数图象也经过点A,B,且mx+5>-(x-b)2 +46+1,根据图象,写出x的取值范围.
16.某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格:x(元/个) … 30 40 50 60 …
销售量y(万个) … 5 4 3 2
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用学过的一次函数、反比例函数或二次函数的之间有关知识求y(万个)与x(元/个)之间的函数解析式.
(2)求该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)之间的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
17.作为武汉市菜篮子工程生产基地,我市新洲区光明村白菜丰收却面临滞销的情况,在武汉市政府的关心和帮助下,各地的订单如雪片般“飞”向光明村,千亩白菜的滞销状况得到较大改善.市政府拟采用水陆联运的方式,派出车队到田间将白菜装车后运往码头再装船销往各地,负责人统计了解装载情况,发现运送到码头的白菜量y(单位:吨)随时间x(单位:小时)的变化情况如图2所示,当0≤x≤10时,y是x的二次函数,图象经过A(0,100),顶点B(10,600);当10<x≤12时,累计数量保持不变.
(1)求y与x之间的函数解析式;
(2)在码头安装了2台传送设备,在运送白菜的同时,可将码头上的白菜直接传送到船上,大大提高了工作效率.每台传送设备每小时可传送20吨白菜到船上.码头上等待传送上船的白菜最多时有多少吨?全部白菜都传送完成需要多少时间?
18.如图,已知二次函数的图像经过,两点.
(1)求该抛物线的解析式及对称轴;
(2)当x为何值时,?
(3)在x轴上方作平行于x轴的直线l,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作x轴的垂线,垂足分别为F,E.当矩形为正方形时,求C点的坐标.
参考答案:
1.B 2.A 3.C 4.B 5.D 6.D 7.C 8.C
9.-1
10.(﹣2,﹣3)
11.
12.
13.;25
14.(1)证明:,
关于的一元二次方程有两个不相等的实数根.
无论取何值,该函数的图象与轴一定有两个交点.
(2)解:由题意,若,
.
当时,
.
.
此时函数图象与轴的交点坐标为和.
15.(1)由已知,得点M的坐标是(b,4b+1).把x=b代入y=4x+1,得y=4b+1,
∴点M在直线y=4x+1上.
(2)由直线y=mx+5与y轴交于点B,得点B坐标为(0,5).又∵点 B(0,5)在抛物线上,代入,得b=2,
∴二次函数的表达式为y=-(x-2)2+9,当y=0时,解得x1=5,x2=-1.
观察图象可得,当mx+5>-(x-b)2+4b+1时,x的取值范围为x<0或x>5.
16.(1)解:根据表格中数据可得出:表中的y与x之间的对应关系为一次函数关系,
设y=kx十b,
由题意得 ,解得 ,
故y(万个)与x(元/个)的函数解析式为y=-0.1x+8
(2)解:由题意得z=(x-20)y-40=(x-20)(-0.1x十8)-40=-0.1x2+10x-200,
即z=-0.1x2十10x-200为这种计算器的净得利润Z(万元)与销售价格x(元/个)的函数解析式
∵z=-0.1x2+10x-200=-0.1(x-50)2+50,
∴当x=50时,Z最大值=50,即销售价格定为50元时净得利润最大,最大值是50万元.
17.(1)解:①当0≤x≤10时,
∵顶点坐标为(10,600),
∴设y=a(x-10)2+600,
将(0,100)代入,得:100a+600=100,
解得a=﹣5,
∴y=﹣5(x﹣10)2+600=﹣5x2+100x+100(0≤x≤10)
②当10<x≤12时,
y=600(10<x≤12),
∴y与x之间的函数表达式为y=
(2)解:设第x小时的等待传送上船的白菜为w吨,由题意可得w=y﹣40x,
①0≤x≤10时,
w=﹣5x2+100x+100﹣40x=﹣5x2+60x+100=﹣5(x﹣6)2+280,
100≤w≤280;当x=10时,w=200,
∵﹣5<0,
∴当x=6时,w的最大值是280;
②0≤x≤10时,100≤w≤280;∵当x=10时,w=200,
∴传送设备一直工作
∴当x>10时,w=600﹣40x,
全部白菜都传送完成,根据题意得:
600﹣40x=0,
解得:x=15
(另:0≤x≤10,一直运送;当x>10时,w=200需5小时,共需15小时)
∴等待传送上船的白菜最多是280吨;
全部白菜都传送完成需要15小时.
18.(1)解:二次函数的图像经过,两点.
,
解得:,
,
,
,
,
对称轴为:直线.
(2)解:当,
,
,
,,
抛物线与轴交点坐标为:,,,,
当时,;
(3)解:当矩形为正方形时,
假设C点坐标为,
点坐标为,,
即:,,
对称轴为:直线,D到对称轴距离等于C到对称轴距离相等,
,
解得:,(不合题意舍去),
时,,
点坐标为:
姓名 班级 学号 成绩
一、选择题:(本题共8小题,每小题5分,共40分.)
1.将方程转化为的形式,则的值为( )
A. B. C. D.
2.将抛物线的图象向右平移个单位,再向下平移个单位,所得图象的解析式为,则( )
A. B. C. D.
3.如图在同一个坐标系中函数和的图象可能的是( )
A.B.C.D.
4.若点,点,点在二次函数的图象上,则,,的大小关系是( )
A. B. C. D.
5.如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
A.1 B. 1.5 C.2 D.3
6.抛物线(其中,是常数)过点,且抛物线的对称轴与线段有交点,点的坐标为,点的坐标为,则的值不可能是( ).
A.9 B.11 C.13 D.15
7.如图所示,已知二次函数的图象与正比例函数的图象交于点,与轴交于点.若,则的取值范围是( ).
A. B. C. D.或
8.如图,直线l的解析式为y=﹣x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是( )
A.B.C.D.
二、填空题:(本题共5小题,每小题3分,共15分.)
9.当m= 时,函数 是二次函数.
10.抛物线y=2x2+8x+5的顶点坐标为 .
11.当时,直线与抛物线有交点,则的取值范围是 .
12.已知二次函数当时,的取值范围是,该二次函数的对称轴为,则的取值范围是 .
13.如图,利用成直角的墙角(墙足够长),用10m长的栅栏围成一个矩形的小花园,花园的面积S(m2)与它一边长a(m)的函数关系式是 ,面积S的最大值是 .
三、解答题:(本题共5题,共45分)
14. 已知二次函数是常数.
(1)求证:无论取何值,该函数的图象与轴一定有两个交点;
(2)取一个你喜欢的的值,并求出此时函数图象与轴的交点坐标.
15.已知M为二次函数y=-(x-b)2+4b+1的图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.
(1)判断顶点M是否在直线y=4x+1上,并说明理由.
(2)如图,若二次函数图象也经过点A,B,且mx+5>-(x-b)2 +46+1,根据图象,写出x的取值范围.
16.某公司销售一种进价为20元/个的计算器,其销售量y(万个)与销售价格x(元/个)的变化如下表:
价格:x(元/个) … 30 40 50 60 …
销售量y(万个) … 5 4 3 2
同时,销售过程中的其他开支(不含进价)总计40万元.
(1)观察并分析表中的y与x之间的对应关系,用学过的一次函数、反比例函数或二次函数的之间有关知识求y(万个)与x(元/个)之间的函数解析式.
(2)求该公司销售这种计算器的净得利润z(万元)与销售价格x(元/个)之间的函数解析式,销售价格定为多少元时净得利润最大,最大值是多少?
17.作为武汉市菜篮子工程生产基地,我市新洲区光明村白菜丰收却面临滞销的情况,在武汉市政府的关心和帮助下,各地的订单如雪片般“飞”向光明村,千亩白菜的滞销状况得到较大改善.市政府拟采用水陆联运的方式,派出车队到田间将白菜装车后运往码头再装船销往各地,负责人统计了解装载情况,发现运送到码头的白菜量y(单位:吨)随时间x(单位:小时)的变化情况如图2所示,当0≤x≤10时,y是x的二次函数,图象经过A(0,100),顶点B(10,600);当10<x≤12时,累计数量保持不变.
(1)求y与x之间的函数解析式;
(2)在码头安装了2台传送设备,在运送白菜的同时,可将码头上的白菜直接传送到船上,大大提高了工作效率.每台传送设备每小时可传送20吨白菜到船上.码头上等待传送上船的白菜最多时有多少吨?全部白菜都传送完成需要多少时间?
18.如图,已知二次函数的图像经过,两点.
(1)求该抛物线的解析式及对称轴;
(2)当x为何值时,?
(3)在x轴上方作平行于x轴的直线l,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作x轴的垂线,垂足分别为F,E.当矩形为正方形时,求C点的坐标.
参考答案:
1.B 2.A 3.C 4.B 5.D 6.D 7.C 8.C
9.-1
10.(﹣2,﹣3)
11.
12.
13.;25
14.(1)证明:,
关于的一元二次方程有两个不相等的实数根.
无论取何值,该函数的图象与轴一定有两个交点.
(2)解:由题意,若,
.
当时,
.
.
此时函数图象与轴的交点坐标为和.
15.(1)由已知,得点M的坐标是(b,4b+1).把x=b代入y=4x+1,得y=4b+1,
∴点M在直线y=4x+1上.
(2)由直线y=mx+5与y轴交于点B,得点B坐标为(0,5).又∵点 B(0,5)在抛物线上,代入,得b=2,
∴二次函数的表达式为y=-(x-2)2+9,当y=0时,解得x1=5,x2=-1.
观察图象可得,当mx+5>-(x-b)2+4b+1时,x的取值范围为x<0或x>5.
16.(1)解:根据表格中数据可得出:表中的y与x之间的对应关系为一次函数关系,
设y=kx十b,
由题意得 ,解得 ,
故y(万个)与x(元/个)的函数解析式为y=-0.1x+8
(2)解:由题意得z=(x-20)y-40=(x-20)(-0.1x十8)-40=-0.1x2+10x-200,
即z=-0.1x2十10x-200为这种计算器的净得利润Z(万元)与销售价格x(元/个)的函数解析式
∵z=-0.1x2+10x-200=-0.1(x-50)2+50,
∴当x=50时,Z最大值=50,即销售价格定为50元时净得利润最大,最大值是50万元.
17.(1)解:①当0≤x≤10时,
∵顶点坐标为(10,600),
∴设y=a(x-10)2+600,
将(0,100)代入,得:100a+600=100,
解得a=﹣5,
∴y=﹣5(x﹣10)2+600=﹣5x2+100x+100(0≤x≤10)
②当10<x≤12时,
y=600(10<x≤12),
∴y与x之间的函数表达式为y=
(2)解:设第x小时的等待传送上船的白菜为w吨,由题意可得w=y﹣40x,
①0≤x≤10时,
w=﹣5x2+100x+100﹣40x=﹣5x2+60x+100=﹣5(x﹣6)2+280,
100≤w≤280;当x=10时,w=200,
∵﹣5<0,
∴当x=6时,w的最大值是280;
②0≤x≤10时,100≤w≤280;∵当x=10时,w=200,
∴传送设备一直工作
∴当x>10时,w=600﹣40x,
全部白菜都传送完成,根据题意得:
600﹣40x=0,
解得:x=15
(另:0≤x≤10,一直运送;当x>10时,w=200需5小时,共需15小时)
∴等待传送上船的白菜最多是280吨;
全部白菜都传送完成需要15小时.
18.(1)解:二次函数的图像经过,两点.
,
解得:,
,
,
,
,
对称轴为:直线.
(2)解:当,
,
,
,,
抛物线与轴交点坐标为:,,,,
当时,;
(3)解:当矩形为正方形时,
假设C点坐标为,
点坐标为,,
即:,,
对称轴为:直线,D到对称轴距离等于C到对称轴距离相等,
,
解得:,(不合题意舍去),
时,,
点坐标为:
同课章节目录
