2023-2024学年苏科版八年级数学上第九周周末提优训练(期中模拟)
文档属性
| 名称 | 2023-2024学年苏科版八年级数学上第九周周末提优训练(期中模拟) |  | |
| 格式 | doc | ||
| 文件大小 | 835.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 08:15:55 | ||
图片预览



文档简介
2023-2024学年苏科版八年级数学上第九周周末提优训练(期中模拟)
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共24分)
1.已知:△ABC≌△DCB,若BC=10cm,AB=5cm,AC=7cm,则CD为( )
A.10cm B.7cm C.5cm D.5cm或7cm
2.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,2.5 B.7,24,25 C.6,12,8 D.9,12,15
3.等腰三角形中,两边的长分别为3和7,则此三角形周长是( )
A.13 B.17 C.13或17 D.15
4.下列各条件中,不能作出唯一三角形的是( )
A.已知两边和夹角 B.已知两角和夹边
C.已知两边和其中一边的对角 D.已知三边
5.一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以达该建筑物的最大高度是( )
A.12米 B.13米 C.14米 D.15米
6.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )
A.75 B.100 C.120 D.125
第6题图 第7题图 第8题图
7.如图,中,,分别为上的点,的平分线分别交于点,若,则的度数为( )
A. B. C. D.
8.如图,已知等边和等边,点在的延长线上,的延长线交于点,连接;下列结论:①;②;③平分④,其中正确的有( )
A.个 B.个 C.个 D.个
二.填空题(每小题3分 共30分)
9.已知等腰三角形的一个内角是80°,则它的底角是 °.
10.AD是△ABC的中线,AB=10,AC=6,则AD的取值范围是 .
11.如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积= .
第11题图 第12题图 第13题图 第14题图
12.已知:如图,在平面上将△ABC绕B点旋转到△A′BC′的位置时,AA′∥BC,∠ABC=70°,则∠CBC′为 度.
13.如图△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于 .
14.如图,圆柱的底面周长为48cm,高为7cm,一只蚂蚁从点B出发沿着圆柱的表面爬行到点A,现有两种路径:①折线B→C→A;②在圆柱侧面上从B到A的一条最短的曲线l.请分别计算这两种路径的长,较短的路径是 .(填①或②).
15.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=18cm,BC=12cm,则DE= cm.
第15题图 第16题图 第17题图 第18题图
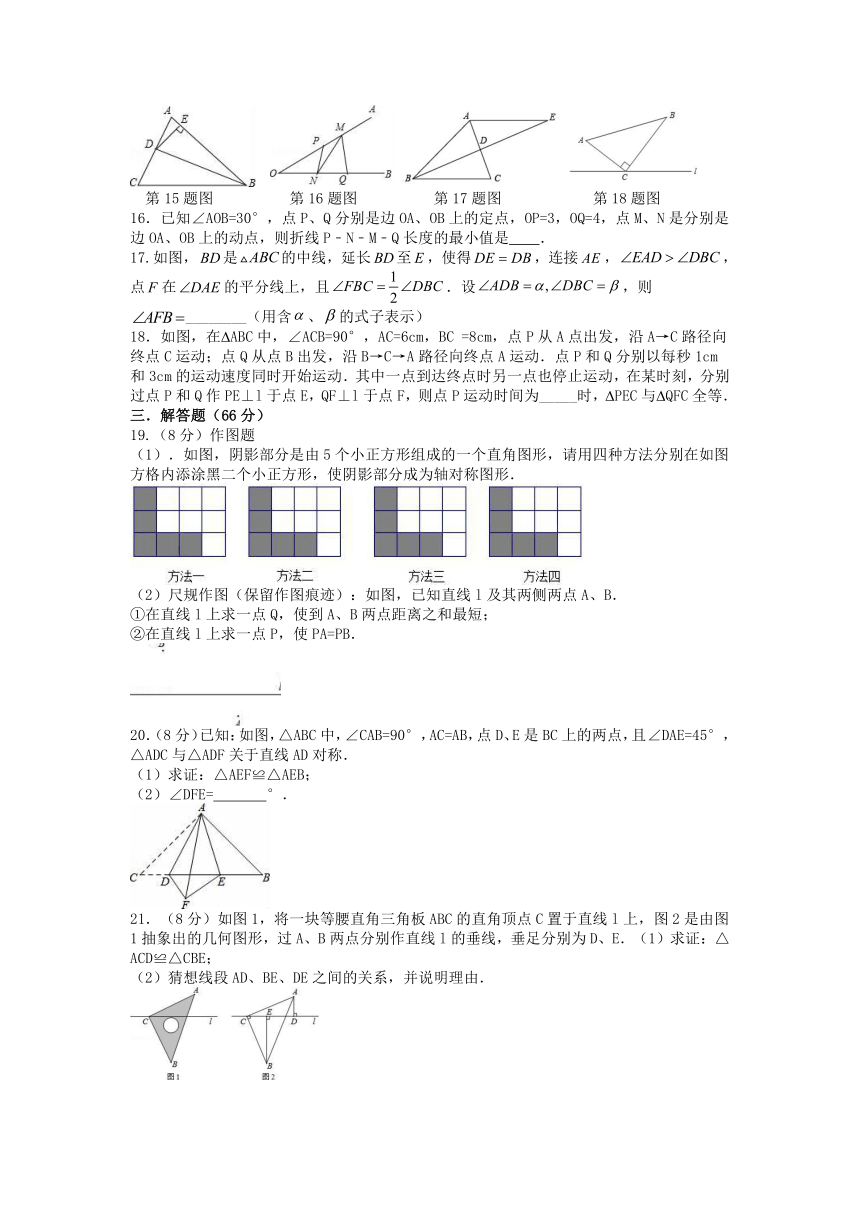
16.已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P﹣N﹣M﹣Q长度的最小值是 .
17.如图,是的中线,延长至,使得,连接,,点在的平分线上,且.设,则________(用含、的式子表示)
18.如图,在 ABC中,∠ACB=90°,AC=6cm,BC =8cm,点P从A点出发,沿A→C路径向终点C运动;点Q从点B出发,沿B→C→A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动.其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥l于点E,QF⊥l于点F,则点P运动时间为_____时, PEC与 QFC全等.
三.解答题(66分)
19.(8分)作图题
(1).如图,阴影部分是由5个小正方形组成的一个直角图形,请用四种方法分别在如图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.
(2)尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.
①在直线l上求一点Q,使到A、B两点距离之和最短;
②在直线l上求一点P,使PA=PB.
20.(8分)已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
(1)求证:△AEF≌△AEB;
(2)∠DFE= °.
21.(8分)如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.(1)求证:△ACD≌△CBE;
(2)猜想线段AD、BE、DE之间的关系,并说明理由.
22.(8分)我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下两组勾股数:11、 ; 13、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
23.(10分)探究:如图1,△ABC是等边三角形,在边CB、AC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F.
(1)求证:△BAE ≌ △CBD ;
(2)∠BFE= °.
应用:将图1的△ABC分别改为正方形ABCM和正五边形ABCMN,如图2、3,在边CB、MC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F,则图2中∠BFE= °;图3中∠BFE= °.
拓展:若将图1的△ABC改为正n边形,其它条件不变,则∠BFE= °(用含n的代数式表示).
24.(12分)(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上,且OC=2cm,动点P从点E沿射线EC以1cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.
25.(12分)(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD、BE之间的数量关系是 .
(2)拓展研究:如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
教师样卷
一.选择题(每小题3分 共24分)
1.已知:△ABC≌△DCB,若BC=10cm,AB=5cm,AC=7cm,则CD为( C )
A.10cm B.7cm C.5cm D.5cm或7cm
2.下列各组数中不能作为直角三角形的三边长的是( C )
A.1.5,2,2.5 B.7,24,25 C.6,12,8 D.9,12,15
3.等腰三角形中,两边的长分别为3和7,则此三角形周长是( B )
A.13 B.17 C.13或17 D.15
4.下列各条件中,不能作出唯一三角形的是( C )
A.已知两边和夹角 B.已知两角和夹边
C.已知两边和其中一边的对角 D.已知三边
5.一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以达该建筑物的最大高度是( A )
A.12米 B.13米 C.14米 D.15米
6.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( B )
A.75 B.100 C.120 D.125
解:∵CE平分∠ACB,CF平分∠ACD,∴∠ACE=∠ACB,∠ACF=∠ACD,即∠ECF=(∠ACB+∠ACD)=90°,∴△EFC为直角三角形,又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,∴CM=EM=MF=5,EF=10,由勾股定理可知CE2+CF2=EF2=100.故选B.
第6题图 第7题图 第8题图
7.如图,中,,分别为上的点,的平分线分别交于点,若,则的度数为( B )
A. B. C. D.
解:∵,∴,∵DF、EG为和的平分线,∴,,在四边形BCED中,有,∴,∴,又∵,∴,∴,∴.故选:B.
8.如图,已知等边和等边,点在的延长线上,的延长线交于点,连接;下列结论:①;②;③平分④,其中正确的有( D )
A.个 B.个 C.个 D.个
解: ①∵等边△ABC 和等边△BPE,∴AB=BC,∠ABC=∠PBE=60°,BP=BE,
在△APB 和△CEB 中,∴△APB≌△CEB(SAS),∴AP=CE,故此选项正确;②∵△APB≌△CEB,∴∠APB=∠CEB,∵∠MCP=∠BCE,则∠PME=∠PBE=60°,故此选项正确;③过点B作BN⊥AM 于N, BF⊥ME 于F,∵△APB≌△CEB,
∴∠BPN=∠FEB,在△BNP 和△BFE 中,,∴△BNP≌△BFE(AAS),∴BN=BF,∴BM 平分∠AME,故此选项正确;④在BM上截取 BK=CM,连接 AK,
由②知∠PME=60°,∴∠AMC=120°,由③知:BM 平分∠AME,∴∠BMC=∠AMK=60°,∴∠AMK=∠ACB=60°,又∵∠AHM=∠BHC,∴∠∠CAM=∠CBH,∵∠CAM+∠ACM=∠EMP=60°,∴∠CBH+∠ACM=60°,∴∠ABK+∠PBM=60°=∠PBM+∠ACM,∴∠ACM=∠ABK, 在△ABK 和△ACM 中
∴△ACM≌△ABK(SAS),∴AK=AM,∴△AMK 为等边三角形,则 AM=MK, 故 AM+MC=BM,故此选项正确;故选D.
二.填空题(每小题3分 共30分)
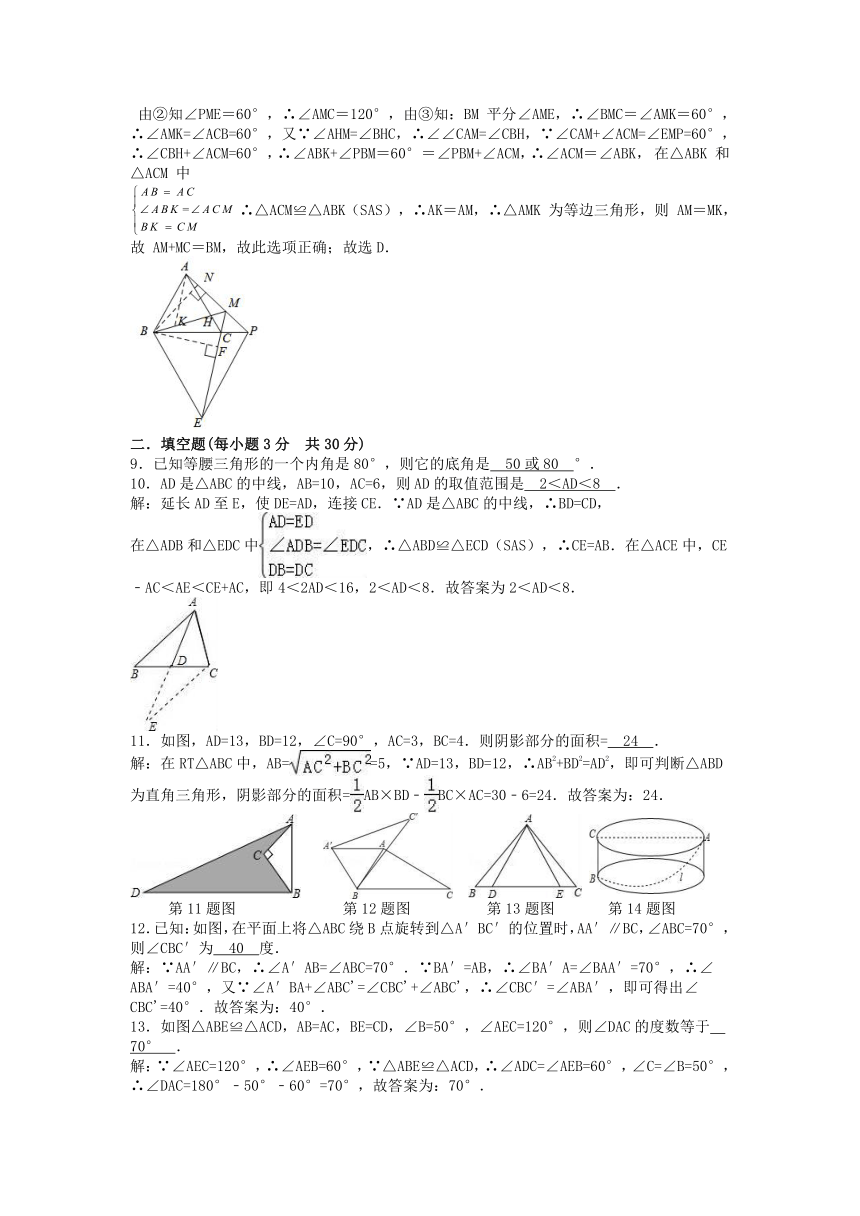
9.已知等腰三角形的一个内角是80°,则它的底角是 50或80 °.
10.AD是△ABC的中线,AB=10,AC=6,则AD的取值范围是 2<AD<8 .
解:延长AD至E,使DE=AD,连接CE.∵AD是△ABC的中线,∴BD=CD,
在△ADB和△EDC中,∴△ABD≌△ECD(SAS),∴CE=AB.在△ACE中,CE﹣AC<AE<CE+AC,即4<2AD<16,2<AD<8.故答案为2<AD<8.
11.如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积= 24 .
解:在RT△ABC中,AB==5,∵AD=13,BD=12,∴AB2+BD2=AD2,即可判断△ABD为直角三角形,阴影部分的面积=AB×BD﹣BC×AC=30﹣6=24.故答案为:24.
第11题图 第12题图 第13题图 第14题图
12.已知:如图,在平面上将△ABC绕B点旋转到△A′BC′的位置时,AA′∥BC,∠ABC=70°,则∠CBC′为 40 度.
解:∵AA′∥BC,∴∠A′AB=∠ABC=70°.∵BA′=AB,∴∠BA′A=∠BAA′=70°,∴∠ABA′=40°,又∵∠A′BA+∠ABC'=∠CBC'+∠ABC',∴∠CBC′=∠ABA′,即可得出∠CBC'=40°.故答案为:40°.
13.如图△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于 70° .
解:∵∠AEC=120°,∴∠AEB=60°,∵△ABE≌△ACD,∴∠ADC=∠AEB=60°,∠C=∠B=50°,
∴∠DAC=180°﹣50°﹣60°=70°,故答案为:70°.
14.如图,圆柱的底面周长为48cm,高为7cm,一只蚂蚁从点B出发沿着圆柱的表面爬行到点A,现有两种路径:①折线B→C→A;②在圆柱侧面上从B到A的一条最短的曲线l.请分别计算这两种路径的长,较短的路径是 ① .(填①或②).
解:①∵圆柱的底面周长为48cm, ∴直径d=cm,∴折线B→C→A=(7+)cm;
②如图所示,AB==25(cm).∵7+<25,∴沿折线B→C→A爬行路径最短.故答案为:①.
15.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=18cm,BC=12cm,则DE= 2 cm.
解:如图,过点D,作DF⊥BC,垂足为点F∵BD是∠ABC的角平分线,DE⊥AB,∴DE=DF
∵△ABC的面积是30cm2,AB=18cm,BC=12cm,∴S△ABC= DE AB+ DF BC,即×18×DE+×12×DE=30,∴DE=2(cm).故填2.
第15题图 第16题图 第17题图 第18题图
16.已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P﹣N﹣M﹣Q长度的最小值是 5 .
解:作P关于OB的对称点P′,作Q关于OA的对称点Q′,连接P′Q′,即为折线P﹣N﹣M﹣Q长度的最小值.根据轴对称的定义可知:∠NOP′=∠AOB=30°,∠OPP′=60°,∴△OPP′为等边三角形,△OQQ′为等边三角形,∴∠P′OQ′=90°,∴在Rt△P′OQ′中,P′Q′==5.故答案为5.
17.如图,是的中线,延长至,使得,连接,,点在的平分线上,且.设,则__或_________(用含、的式子表示)
解:∵BD是△ABC的中线,∴AD=DC,∵在△BDC和△EDA中,∴△BDC≌△EDA(SAS),∴∠C=∠EAD,∵点F在∠DAE的平分线上,∴∠FAD=∠EAD=∠C,∵∠ADB=α,∠DBC=β,∴∠C=α β,∠DAB+∠DBA=180° α,∴∠FAD=(α β),∴∠AFB=180° ∠FAB ∠FBA=180° ∠DAB ∠DBA ∠FAD ∠FBD=180° (180° α) (α β) ∠FBD=α+β ∠FBD∵∠FBC=∠DBC=β,当射线BF在∠DBC内部时,∴∠FBD=β,∴∠AFB=α+β β=α;当射线BF在∠DBC外部时,则∠FBD=β,∴∠AFB=α+β β=α β,综上,∠AFB=α或α β,故答案为:α或α β.
18.如图,在 ABC中,∠ACB=90°,AC=6cm,BC =8cm,点P从A点出发,沿A→C路径向终点C运动;点Q从点B出发,沿B→C→A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动.其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥l于点E,QF⊥l于点F,则点P运动时间为_1s或3.5s____时, PEC与 QFC全等.
解:设运动时间为t秒时,△PEC≌△CFQ,∵△PEC≌△CFQ,∴斜边CP=CQ,有2种情况:①P在AC上,Q在BC上,CP=6-t,CQ=8-3t,∴6-t=8-3t,∴t=1;
②P、Q都在AC上,此时P、Q重合,∴CP=6-t=3t-8,∴t=3.5;答:点P运动1s或3.5s时,△PEC与△QFC全等.故答案为:1s或3.5s.
三.解答题(66分)
19.(8分)作图题
(1).如图,阴影部分是由5个小正方形组成的一个直角图形,请用四种方法分别在如图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.
解:如图所示:
(2)尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.
①在直线l上求一点Q,使到A、B两点距离之和最短;
②在直线l上求一点P,使PA=PB.
解:如图所示:
20.(8分)已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
(1)求证:△AEF≌△AEB;
(2)∠DFE= °.
解:(1)∵把△ADC沿着AD折叠,得到△ADF,∴△AFD≌△ADC;∴AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD,∵AB=AC,∴AF=AB,∵∠DAE=45°,∴∠FAE=∠BAE,
在△AFE与△ACE中,,∴△AFE≌△ABE,
(2)由(1)知△AFE≌△ABE,∴∠AFE=∠C,EF=EC,∴∠DFE=∠DFA+∠EFA=∠B+∠C=90°.故答案为:90°.
21.(8分)如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.(1)求证:△ACD≌△CBE;
(2)猜想线段AD、BE、DE之间的关系,并说明理由.
证明:(1)∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°,又∵∠ACB=90°,∴∠ACD=∠CBE=90°﹣∠ECB.在△ACD与△CBE中,,∴△ACD≌△CBE(AAS);(2)AD=BE﹣DE,理由如下:∵△ACD≌△CBE,∴CD=BE,AD=CE,又∵CE=CD﹣DE,∴AD=BE﹣DE
22.(8分)我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下两组勾股数:11、 ; 13、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
解:(1)∵3、4、5;5、12、13;7、24、25;9、40、41;…,∴4=,12=,24=…∴11,60,61;13,84,85; 故答案为:60,61;84,85;
(2)后两个数表示为和,∵a2+()2=a2+==,=,
∴a2+()2=,又∵a≥3,且a为奇数,∴由a,,三个数组成的数是勾股数. 故答案为:,.
23.(10分)探究:如图1,△ABC是等边三角形,在边CB、AC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F.
(1)求证:△BAE ≌ △CBD ;
(2)∠BFE= °.
应用:将图1的△ABC分别改为正方形ABCM和正五边形ABCMN,如图2、3,在边CB、MC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F,则图2中∠BFE= °;图3中∠BFE= °.
拓展:若将图1的△ABC改为正n边形,其它条件不变,则∠BFE= °(用含n的代数式表示).
解:(1)∵△BCA是等边三角形,∴BC=AB,∠ACB=∠ABC=60°.∴∠BCD=∠ABE=120°
在△CBD和△BAE中,∴△CBD ≌ △BAE.
(2)∠BFE = 120 °. 图2中∠BFE = 90 °; 图3中∠BFE = 72 °. 拓展∠BFE = °
24.(12分)(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上,且OC=2cm,动点P从点E沿射线EC以1cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.
解:(1)证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,∴∠DAC=ECB,在△ADC和△CEB中,∴△ADC≌△CEB;
(2)如图1,根据题意得出旋转后图形,AC′⊥AC,B′D′⊥AC,∵∠C′AC=∠AC′B′=∠AD′B′,
∴四边形C′AD′B′是矩形,∴AC′=B′D′=AC=4,∴S△AB′C=AC×B′D′=×4×4=8;
(3)如图2,∵△BCE是等边三角形,∴∠CBE=∠BCE=60°,∴∠OBF=∠OCP=120°,∴∠BOF+∠BFO=60°,∵∠POF=120°,∴∠BOF+∠OPC=60°,∴∠BFO=∠CPO,∵OP=OF,
∴△OCP≌△FBO,∴CP=BO=BC﹣OC=3﹣2=1,∴EP=EC+CP=3+1=4,∵动点P从点E沿射线EC以1cm/s速度运动,∴t=4÷1=4s.
25.(12分)(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD、BE之间的数量关系是 .
(2)拓展研究:如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
解:(1)①如图1,∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.∵△DCE为等边三角形,∴∠CDE=∠CED=60°.∵点A,D,E在同一直线上,∴∠ADC=120°.∴∠BEC=120°.∴∠AEB=∠BEC﹣∠CED=60°.故答案为:60°.
②∵△ACD≌△BCE,∴AD=BE.故答案为:AD=BE.
(2)∵△ACB和△DCE均为等腰直角三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=90°.∴∠ACD=∠BCE.在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).∴AD=BE=AE﹣DE=8=,∠ADC=∠BEC,∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,∴∠ADC=135°.∴∠BEC=135°.∴∠AEB=∠BEC﹣∠CED=90°.
∴AB==17;
(3)如图3,由(1)知△ACD≌△BCE,∴∠CAD=∠CBE,∵∠CAB=∠CBA=60°,∴∠OAB+∠OBA=120°∴∠AOE=180°﹣120°=60°,如图4,同理求得∠AOB=60°,AOE=120°,∴∠AOE的度数是60°或120°.
(时间:90分钟 满分:120分)
一.选择题(每小题3分 共24分)
1.已知:△ABC≌△DCB,若BC=10cm,AB=5cm,AC=7cm,则CD为( )
A.10cm B.7cm C.5cm D.5cm或7cm
2.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,2.5 B.7,24,25 C.6,12,8 D.9,12,15
3.等腰三角形中,两边的长分别为3和7,则此三角形周长是( )
A.13 B.17 C.13或17 D.15
4.下列各条件中,不能作出唯一三角形的是( )
A.已知两边和夹角 B.已知两角和夹边
C.已知两边和其中一边的对角 D.已知三边
5.一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以达该建筑物的最大高度是( )
A.12米 B.13米 C.14米 D.15米
6.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )
A.75 B.100 C.120 D.125
第6题图 第7题图 第8题图
7.如图,中,,分别为上的点,的平分线分别交于点,若,则的度数为( )
A. B. C. D.
8.如图,已知等边和等边,点在的延长线上,的延长线交于点,连接;下列结论:①;②;③平分④,其中正确的有( )
A.个 B.个 C.个 D.个
二.填空题(每小题3分 共30分)
9.已知等腰三角形的一个内角是80°,则它的底角是 °.
10.AD是△ABC的中线,AB=10,AC=6,则AD的取值范围是 .
11.如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积= .
第11题图 第12题图 第13题图 第14题图
12.已知:如图,在平面上将△ABC绕B点旋转到△A′BC′的位置时,AA′∥BC,∠ABC=70°,则∠CBC′为 度.
13.如图△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于 .
14.如图,圆柱的底面周长为48cm,高为7cm,一只蚂蚁从点B出发沿着圆柱的表面爬行到点A,现有两种路径:①折线B→C→A;②在圆柱侧面上从B到A的一条最短的曲线l.请分别计算这两种路径的长,较短的路径是 .(填①或②).
15.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=18cm,BC=12cm,则DE= cm.
第15题图 第16题图 第17题图 第18题图
16.已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P﹣N﹣M﹣Q长度的最小值是 .
17.如图,是的中线,延长至,使得,连接,,点在的平分线上,且.设,则________(用含、的式子表示)
18.如图,在 ABC中,∠ACB=90°,AC=6cm,BC =8cm,点P从A点出发,沿A→C路径向终点C运动;点Q从点B出发,沿B→C→A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动.其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥l于点E,QF⊥l于点F,则点P运动时间为_____时, PEC与 QFC全等.
三.解答题(66分)
19.(8分)作图题
(1).如图,阴影部分是由5个小正方形组成的一个直角图形,请用四种方法分别在如图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.
(2)尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.
①在直线l上求一点Q,使到A、B两点距离之和最短;
②在直线l上求一点P,使PA=PB.
20.(8分)已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
(1)求证:△AEF≌△AEB;
(2)∠DFE= °.
21.(8分)如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.(1)求证:△ACD≌△CBE;
(2)猜想线段AD、BE、DE之间的关系,并说明理由.
22.(8分)我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下两组勾股数:11、 ; 13、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
23.(10分)探究:如图1,△ABC是等边三角形,在边CB、AC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F.
(1)求证:△BAE ≌ △CBD ;
(2)∠BFE= °.
应用:将图1的△ABC分别改为正方形ABCM和正五边形ABCMN,如图2、3,在边CB、MC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F,则图2中∠BFE= °;图3中∠BFE= °.
拓展:若将图1的△ABC改为正n边形,其它条件不变,则∠BFE= °(用含n的代数式表示).
24.(12分)(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上,且OC=2cm,动点P从点E沿射线EC以1cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.
25.(12分)(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD、BE之间的数量关系是 .
(2)拓展研究:如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
教师样卷
一.选择题(每小题3分 共24分)
1.已知:△ABC≌△DCB,若BC=10cm,AB=5cm,AC=7cm,则CD为( C )
A.10cm B.7cm C.5cm D.5cm或7cm
2.下列各组数中不能作为直角三角形的三边长的是( C )
A.1.5,2,2.5 B.7,24,25 C.6,12,8 D.9,12,15
3.等腰三角形中,两边的长分别为3和7,则此三角形周长是( B )
A.13 B.17 C.13或17 D.15
4.下列各条件中,不能作出唯一三角形的是( C )
A.已知两边和夹角 B.已知两角和夹边
C.已知两边和其中一边的对角 D.已知三边
5.一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以达该建筑物的最大高度是( A )
A.12米 B.13米 C.14米 D.15米
6.如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( B )
A.75 B.100 C.120 D.125
解:∵CE平分∠ACB,CF平分∠ACD,∴∠ACE=∠ACB,∠ACF=∠ACD,即∠ECF=(∠ACB+∠ACD)=90°,∴△EFC为直角三角形,又∵EF∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠ECB=∠MEC=∠ECM,∠DCF=∠CFM=∠MCF,∴CM=EM=MF=5,EF=10,由勾股定理可知CE2+CF2=EF2=100.故选B.
第6题图 第7题图 第8题图
7.如图,中,,分别为上的点,的平分线分别交于点,若,则的度数为( B )
A. B. C. D.
解:∵,∴,∵DF、EG为和的平分线,∴,,在四边形BCED中,有,∴,∴,又∵,∴,∴,∴.故选:B.
8.如图,已知等边和等边,点在的延长线上,的延长线交于点,连接;下列结论:①;②;③平分④,其中正确的有( D )
A.个 B.个 C.个 D.个
解: ①∵等边△ABC 和等边△BPE,∴AB=BC,∠ABC=∠PBE=60°,BP=BE,
在△APB 和△CEB 中,∴△APB≌△CEB(SAS),∴AP=CE,故此选项正确;②∵△APB≌△CEB,∴∠APB=∠CEB,∵∠MCP=∠BCE,则∠PME=∠PBE=60°,故此选项正确;③过点B作BN⊥AM 于N, BF⊥ME 于F,∵△APB≌△CEB,
∴∠BPN=∠FEB,在△BNP 和△BFE 中,,∴△BNP≌△BFE(AAS),∴BN=BF,∴BM 平分∠AME,故此选项正确;④在BM上截取 BK=CM,连接 AK,
由②知∠PME=60°,∴∠AMC=120°,由③知:BM 平分∠AME,∴∠BMC=∠AMK=60°,∴∠AMK=∠ACB=60°,又∵∠AHM=∠BHC,∴∠∠CAM=∠CBH,∵∠CAM+∠ACM=∠EMP=60°,∴∠CBH+∠ACM=60°,∴∠ABK+∠PBM=60°=∠PBM+∠ACM,∴∠ACM=∠ABK, 在△ABK 和△ACM 中
∴△ACM≌△ABK(SAS),∴AK=AM,∴△AMK 为等边三角形,则 AM=MK, 故 AM+MC=BM,故此选项正确;故选D.
二.填空题(每小题3分 共30分)
9.已知等腰三角形的一个内角是80°,则它的底角是 50或80 °.
10.AD是△ABC的中线,AB=10,AC=6,则AD的取值范围是 2<AD<8 .
解:延长AD至E,使DE=AD,连接CE.∵AD是△ABC的中线,∴BD=CD,
在△ADB和△EDC中,∴△ABD≌△ECD(SAS),∴CE=AB.在△ACE中,CE﹣AC<AE<CE+AC,即4<2AD<16,2<AD<8.故答案为2<AD<8.
11.如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积= 24 .
解:在RT△ABC中,AB==5,∵AD=13,BD=12,∴AB2+BD2=AD2,即可判断△ABD为直角三角形,阴影部分的面积=AB×BD﹣BC×AC=30﹣6=24.故答案为:24.
第11题图 第12题图 第13题图 第14题图
12.已知:如图,在平面上将△ABC绕B点旋转到△A′BC′的位置时,AA′∥BC,∠ABC=70°,则∠CBC′为 40 度.
解:∵AA′∥BC,∴∠A′AB=∠ABC=70°.∵BA′=AB,∴∠BA′A=∠BAA′=70°,∴∠ABA′=40°,又∵∠A′BA+∠ABC'=∠CBC'+∠ABC',∴∠CBC′=∠ABA′,即可得出∠CBC'=40°.故答案为:40°.
13.如图△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数等于 70° .
解:∵∠AEC=120°,∴∠AEB=60°,∵△ABE≌△ACD,∴∠ADC=∠AEB=60°,∠C=∠B=50°,
∴∠DAC=180°﹣50°﹣60°=70°,故答案为:70°.
14.如图,圆柱的底面周长为48cm,高为7cm,一只蚂蚁从点B出发沿着圆柱的表面爬行到点A,现有两种路径:①折线B→C→A;②在圆柱侧面上从B到A的一条最短的曲线l.请分别计算这两种路径的长,较短的路径是 ① .(填①或②).
解:①∵圆柱的底面周长为48cm, ∴直径d=cm,∴折线B→C→A=(7+)cm;
②如图所示,AB==25(cm).∵7+<25,∴沿折线B→C→A爬行路径最短.故答案为:①.
15.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=18cm,BC=12cm,则DE= 2 cm.
解:如图,过点D,作DF⊥BC,垂足为点F∵BD是∠ABC的角平分线,DE⊥AB,∴DE=DF
∵△ABC的面积是30cm2,AB=18cm,BC=12cm,∴S△ABC= DE AB+ DF BC,即×18×DE+×12×DE=30,∴DE=2(cm).故填2.
第15题图 第16题图 第17题图 第18题图
16.已知∠AOB=30°,点P、Q分别是边OA、OB上的定点,OP=3,OQ=4,点M、N是分别是边OA、OB上的动点,则折线P﹣N﹣M﹣Q长度的最小值是 5 .
解:作P关于OB的对称点P′,作Q关于OA的对称点Q′,连接P′Q′,即为折线P﹣N﹣M﹣Q长度的最小值.根据轴对称的定义可知:∠NOP′=∠AOB=30°,∠OPP′=60°,∴△OPP′为等边三角形,△OQQ′为等边三角形,∴∠P′OQ′=90°,∴在Rt△P′OQ′中,P′Q′==5.故答案为5.
17.如图,是的中线,延长至,使得,连接,,点在的平分线上,且.设,则__或_________(用含、的式子表示)
解:∵BD是△ABC的中线,∴AD=DC,∵在△BDC和△EDA中,∴△BDC≌△EDA(SAS),∴∠C=∠EAD,∵点F在∠DAE的平分线上,∴∠FAD=∠EAD=∠C,∵∠ADB=α,∠DBC=β,∴∠C=α β,∠DAB+∠DBA=180° α,∴∠FAD=(α β),∴∠AFB=180° ∠FAB ∠FBA=180° ∠DAB ∠DBA ∠FAD ∠FBD=180° (180° α) (α β) ∠FBD=α+β ∠FBD∵∠FBC=∠DBC=β,当射线BF在∠DBC内部时,∴∠FBD=β,∴∠AFB=α+β β=α;当射线BF在∠DBC外部时,则∠FBD=β,∴∠AFB=α+β β=α β,综上,∠AFB=α或α β,故答案为:α或α β.
18.如图,在 ABC中,∠ACB=90°,AC=6cm,BC =8cm,点P从A点出发,沿A→C路径向终点C运动;点Q从点B出发,沿B→C→A路径向终点A运动.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动.其中一点到达终点时另一点也停止运动,在某时刻,分别过点P和Q作PE⊥l于点E,QF⊥l于点F,则点P运动时间为_1s或3.5s____时, PEC与 QFC全等.
解:设运动时间为t秒时,△PEC≌△CFQ,∵△PEC≌△CFQ,∴斜边CP=CQ,有2种情况:①P在AC上,Q在BC上,CP=6-t,CQ=8-3t,∴6-t=8-3t,∴t=1;
②P、Q都在AC上,此时P、Q重合,∴CP=6-t=3t-8,∴t=3.5;答:点P运动1s或3.5s时,△PEC与△QFC全等.故答案为:1s或3.5s.
三.解答题(66分)
19.(8分)作图题
(1).如图,阴影部分是由5个小正方形组成的一个直角图形,请用四种方法分别在如图方格内添涂黑二个小正方形,使阴影部分成为轴对称图形.
解:如图所示:
(2)尺规作图(保留作图痕迹):如图,已知直线l及其两侧两点A、B.
①在直线l上求一点Q,使到A、B两点距离之和最短;
②在直线l上求一点P,使PA=PB.
解:如图所示:
20.(8分)已知:如图,△ABC中,∠CAB=90°,AC=AB,点D、E是BC上的两点,且∠DAE=45°,△ADC与△ADF关于直线AD对称.
(1)求证:△AEF≌△AEB;
(2)∠DFE= °.
解:(1)∵把△ADC沿着AD折叠,得到△ADF,∴△AFD≌△ADC;∴AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD,∵AB=AC,∴AF=AB,∵∠DAE=45°,∴∠FAE=∠BAE,
在△AFE与△ACE中,,∴△AFE≌△ABE,
(2)由(1)知△AFE≌△ABE,∴∠AFE=∠C,EF=EC,∴∠DFE=∠DFA+∠EFA=∠B+∠C=90°.故答案为:90°.
21.(8分)如图1,将一块等腰直角三角板ABC的直角顶点C置于直线l上,图2是由图1抽象出的几何图形,过A、B两点分别作直线l的垂线,垂足分别为D、E.(1)求证:△ACD≌△CBE;
(2)猜想线段AD、BE、DE之间的关系,并说明理由.
证明:(1)∵AD⊥CE,BE⊥CE,∴∠ADC=∠CEB=90°,又∵∠ACB=90°,∴∠ACD=∠CBE=90°﹣∠ECB.在△ACD与△CBE中,,∴△ACD≌△CBE(AAS);(2)AD=BE﹣DE,理由如下:∵△ACD≌△CBE,∴CD=BE,AD=CE,又∵CE=CD﹣DE,∴AD=BE﹣DE
22.(8分)我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下两组勾股数:11、 ; 13、 ;
(2)若第一个数用字母a(a为奇数,且a≥3)表示,那么后两个数用含a的代数式分别表示为 和 ,请用所学知识说明它们是一组勾股数.
解:(1)∵3、4、5;5、12、13;7、24、25;9、40、41;…,∴4=,12=,24=…∴11,60,61;13,84,85; 故答案为:60,61;84,85;
(2)后两个数表示为和,∵a2+()2=a2+==,=,
∴a2+()2=,又∵a≥3,且a为奇数,∴由a,,三个数组成的数是勾股数. 故答案为:,.
23.(10分)探究:如图1,△ABC是等边三角形,在边CB、AC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F.
(1)求证:△BAE ≌ △CBD ;
(2)∠BFE= °.
应用:将图1的△ABC分别改为正方形ABCM和正五边形ABCMN,如图2、3,在边CB、MC的延长线上截取BE=CD,连结BD、AE,延长DB交AE于点F,则图2中∠BFE= °;图3中∠BFE= °.
拓展:若将图1的△ABC改为正n边形,其它条件不变,则∠BFE= °(用含n的代数式表示).
解:(1)∵△BCA是等边三角形,∴BC=AB,∠ACB=∠ABC=60°.∴∠BCD=∠ABE=120°
在△CBD和△BAE中,∴△CBD ≌ △BAE.
(2)∠BFE = 120 °. 图2中∠BFE = 90 °; 图3中∠BFE = 72 °. 拓展∠BFE = °
24.(12分)(1)观察推理:如图1,△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A、B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D、E.求证:△AEC≌△CDB;
(2)类比探究:如图2,Rt△ABC中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,求△AB′C的面积.
(3)拓展提升:如图3,等边△EBC中,EC=BC=3cm,点O在BC上,且OC=2cm,动点P从点E沿射线EC以1cm/s速度运动,连结OP,将线段OP绕点O逆时针旋转120°得到线段OF.要使点F恰好落在射线EB上,求点P运动的时间ts.
解:(1)证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,∴∠DAC=ECB,在△ADC和△CEB中,∴△ADC≌△CEB;
(2)如图1,根据题意得出旋转后图形,AC′⊥AC,B′D′⊥AC,∵∠C′AC=∠AC′B′=∠AD′B′,
∴四边形C′AD′B′是矩形,∴AC′=B′D′=AC=4,∴S△AB′C=AC×B′D′=×4×4=8;
(3)如图2,∵△BCE是等边三角形,∴∠CBE=∠BCE=60°,∴∠OBF=∠OCP=120°,∴∠BOF+∠BFO=60°,∵∠POF=120°,∴∠BOF+∠OPC=60°,∴∠BFO=∠CPO,∵OP=OF,
∴△OCP≌△FBO,∴CP=BO=BC﹣OC=3﹣2=1,∴EP=EC+CP=3+1=4,∵动点P从点E沿射线EC以1cm/s速度运动,∴t=4÷1=4s.
25.(12分)(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;②线段AD、BE之间的数量关系是 .
(2)拓展研究:如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
解:(1)①如图1,∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.∵△DCE为等边三角形,∴∠CDE=∠CED=60°.∵点A,D,E在同一直线上,∴∠ADC=120°.∴∠BEC=120°.∴∠AEB=∠BEC﹣∠CED=60°.故答案为:60°.
②∵△ACD≌△BCE,∴AD=BE.故答案为:AD=BE.
(2)∵△ACB和△DCE均为等腰直角三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=90°.∴∠ACD=∠BCE.在△ACD和△BCE中,,∴△ACD≌△BCE(SAS).∴AD=BE=AE﹣DE=8=,∠ADC=∠BEC,∵△DCE为等腰直角三角形,∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,∴∠ADC=135°.∴∠BEC=135°.∴∠AEB=∠BEC﹣∠CED=90°.
∴AB==17;
(3)如图3,由(1)知△ACD≌△BCE,∴∠CAD=∠CBE,∵∠CAB=∠CBA=60°,∴∠OAB+∠OBA=120°∴∠AOE=180°﹣120°=60°,如图4,同理求得∠AOB=60°,AOE=120°,∴∠AOE的度数是60°或120°.
同课章节目录
