空间几何体的三视图
图片预览










文档简介
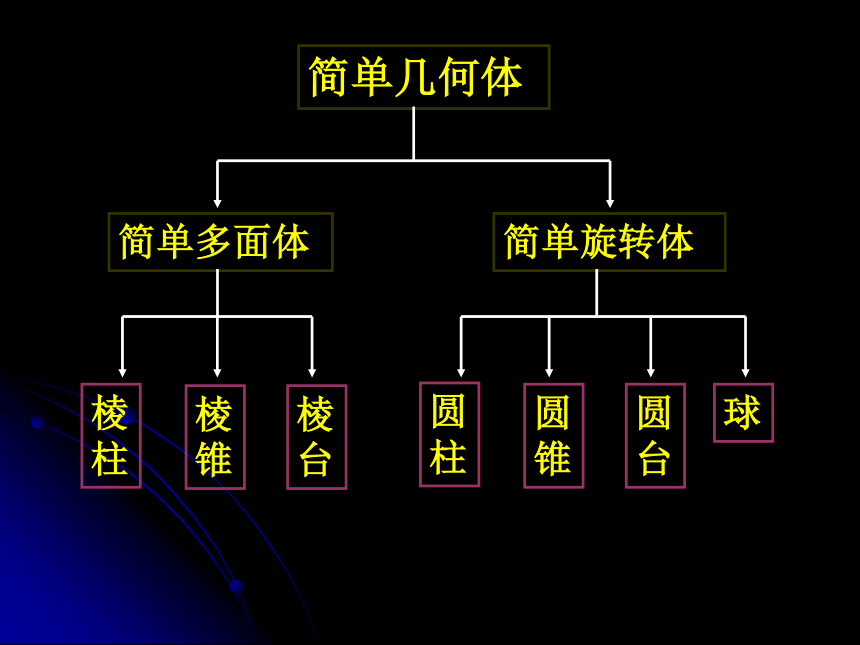
课件50张PPT。空间几何体
的三视图简单几何体简单旋转体简单多面体球圆
柱圆
锥圆
台棱
柱棱
锥棱
台从立体图形
到平面图形体会:从实物图到立体图形,从立体图形到平面图形的过程并掌握其方法。中心投影与平行投影皮影戏表演中心投影与平行投影 我们知道,光是直线传播的.由于光的照射,在不透明
物体后面的屏幕上可以留下这个物体的影子,这种现象
叫做投影.我们把光线叫做投影线,把留下物体影子的
屏幕叫做投影面.生活有许多投影的例子,下面看一个例子----手影中心投影我们把光由一点向外散射形成的投影,叫做中心投影中心投影的投影线交于一点.中心投影现象在我们的日常生活中非常普遍.例如,在电灯泡的照射下,物体后面的屏幕上就会形成
影子,而且随着物体距离灯泡的远近,形成的影子大小
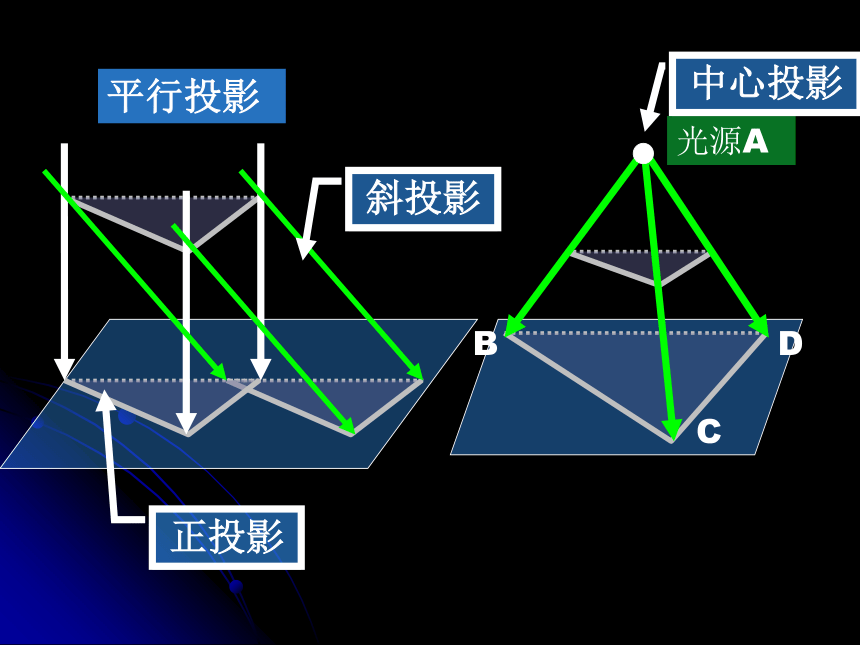
就会有所不同. 人的视觉、照片、美术作品都具有中心投影的特点.平行投影 我们把在一束平行光线照射下形成的投影,叫做
平行投影. 平行投影的投影是平行的,在平行投影中,投影线
正对着投影面时,叫做正投影,否则叫做斜投影. 在平行投影之下,与投影面平行的平面图形留下
的影子,与这个平面图形的形状和大小完全相同的. 下面看看一个三角板在中心投影和不同方向的
平行投影之下,所产生的投影.正投影:投影线与投影面垂直斜投影:投影线与投影面不垂直光源A中心投影平行投影斜投影正投影 我们从不同的方向观察同一个物体时,可能看到不同的图形.为了能完整确切地表达物体的形状和大小,必须从多方面观察物体.在几何中,我们通常选择从正面、上面、左面三个方向观察物体。 这样就把一个立体图形用几个平面图形来描述图2图1 在生活和生产实践中,我们经常需要用从多个方向看到的图形来描述物体的形状和大小,如下图 2 所示就是图 1 所示的热水瓶从不同方向看到的图形.——三视图初步感知三视图的形成OxyzVHW
如图所示, 为了表达物体的形状,往往需要把物体向几个不同平面分别作正投影,通常采用互相垂直的三个投影面,建立一个三面投影体系。三视图的形成 一个投影面正立放置,叫做正立投影面,投影到这个平面内的图形叫做正视图(主视图),即光线从几何体的前面向后面正投影,得到的投影图 三视图的形成 一个投影面水平放置,叫做水平投影面,投影到这个平面的图象叫做俯视图, 即光线从几何体的上面向下面正投影,得到的投影图; 三视图的形成 和正立、水平两个投射面都垂直的投射面叫做侧立投影面,通常把这个平面放在正立投影面的右面,投射到这个平面内的图形叫做侧视图(左视图),即光线从几何体的左面向右面正投影,得到的投影图。正视图、俯视图和侧视图统称为几何体的三视图.俯视图三视图的对应规律 观察:正视图、侧视图和俯视图分别是从几何体的正前方、正左方和正上方观察到的几何体的正投影图,它们都是平面图形。观察长方体的三视图,你能得出同一个几何体的正视图、侧视图和俯视图在形状、大小方面的关系吗?俯视图正
视
图正视图俯视图侧视图a a bbcca bc 一个物体的三视图的排列规则是:俯视图放在正视图的下面,长度与正视图一样,侧视图放在正视图的右面,高度与正视图一样,宽度与俯视图的宽度一样,即
“长对正、高平齐、宽相等”
它是指:正视图和俯视图一样长;正视图和侧视图一样高;俯视图和侧视图一样宽
正视图反映出物体的长和高,俯视图反映出物体的长和宽,侧视图反映出物体的高和宽.三视图的对应规律例 1 画出下列几何体的三视图 从立体图形到平面图形从立体图形到平面图形解: 圆柱的三视图如下: 正视图侧视图俯视图从立体图形到平面图形解: 圆锥的三视图如下: 正视图侧视图俯视图解: 此几何体的三视图如下: 从立体图形到平面图形正视图侧视图俯视图虚实:在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.注:若相邻的两平面的相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出正三棱锥的三视图正视图俯视图侧视图长对正高平齐宽相等画下面正六棱柱的三视图画下面六棱柱的三视图正视图俯视图侧视图练习 画出正四棱柱、正六棱柱的三视图 从立体图形到平面图形主从立体图形到平面图形解: 正六棱柱的三视图如下: 正视图 侧视图俯视图 正六棱柱正视图 侧视图 俯视图 解: 正六棱柱的三视图如下: 从立体图形到平面图形1.确定正视图方向3.先画出能反映物体真实形
状的一个视图 4.运用
原则画出其它视图5.检查、修正2.布置视图 长对正、高平齐、宽相等注意:俯视图安排在正视图的正下方,侧视图安排在正视图的正右方. 主视图侧视图俯视图三视图的作图步骤 正视图侧视图俯视图注:看得见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.正视图侧视图俯视图从平面图形到立体图形例 2 根据下列的三视图画出几何体简单几何体的三视图下列物体表示的几何体是一些简单几何体的组合
体,你能画出它们的三视图吗?对于简单几何体的组合体,必须认真观察
它的基本结构,然后再画它的三视图.图(1)的几何结构,从上到下分别是圆柱,
圆台和圆柱,它的三视图如左图所示.对于简单组合体同样也要符合三视图的对应规律.简单几何体的三视图知识小结投影平行投影中心投影斜投影正投影1.投影正视图
侧视图
俯视图
画物体的三视图时,要符合如下原则:
位置:正视图 侧视图
俯视图
2.大小:长对正,高平齐,宽相等
3.虚实: 在画图时,看得见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.知识小结2.三视图——从正面看到的图——从左面看到的图——从上面看到的图复习 在物体的平行投影中, 如果投影线与投影面垂直, 则称这样的平行投影为正投影. 正投影除具有平行投影的性质外, 还有以下性质:
(1)垂直于投影面的直线或线段的正投影是 点 ;
(2)垂直于投影面的平面图形的正投影是 直线
或直线的一部分.1. 中心投影、平行投影、正投影的定义2. 正投影的性质:
正视图——从正面看到的图
侧视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:正视图 侧视图
俯视图
大小:长对正,高平齐,宽相等3.三视图对几何体的三视图, 下列说法正确的是
正视图反映物体的长和宽
俯视图反映物体的长和高
侧视图反映物体的高和宽
正视图反映物体的高和宽2. 一个几何体的三视图如果相同, 那么这个几何体
可能是
A. 长方体 B. 正方体
C. 球 D. 正方体或球练习三视图表达的意义 从前面正对着物体观察,画出正视图,正视图反映了物体的长和高及前后两个面的实形。
从上向下正对着物体观察,画出俯视图,布置在正视图的正下方,俯视图反映了物体的长和宽及上下两个面的实形。
从左向右正对着物体观察,画出侧视图,布置在正视图的正右方,侧视图反映了物体的宽和高及左右两个面的实形。三视图能反映物体真实的形状和长、宽、高 注意:
若相邻两物体的表面相交,表面的交线是它们的边界线. 在三视图中,边界线和可见轮廓线都用实线画出;
在画三视图时,不可见轮廓线用虚线画出
绘制与检查时,应先从整体到局部顺序进行;
先定正视俯视左视方向,同一物体放的位置不同,三视图可能不一样;
观察组合体由哪些基本几何体形成,什么形成方式,交线位置如何.正方形正方形正方形矩形矩形矩形矩形矩形圆圆圆圆圆圆等腰三角形 等腰三角形等腰梯形等腰梯形归纳简单几何体的三视图: 例2 由5个相同的小立方块搭成的几何体如图所示,请画出它的三视图:侧视图俯视图正视图解: 所求三视图如图主视方向上题作如下变化(如图所示),请画出它的三视图:侧视图俯视图正视图解: 所求三视图如图主视方向解: 所求三视图如图: 左图是由七个小正方体组成的物体的俯视图,上面的数字表示这一位置小正方体的个数,你能画出它的另外两个视图吗?俯视图11221主视方向 一个骰子由 1 ~ 6 六个数字组成, 请根据下图A, B, C 三种状态所显示的数字, 推出 “ ? ” 处的数字是( )A. 6 B. 3 C. 1 D. 2A针对性练习1.课后练习 P152.名师一号P9--10 第1, 2, 3, 4, 6, 10题
的三视图简单几何体简单旋转体简单多面体球圆
柱圆
锥圆
台棱
柱棱
锥棱
台从立体图形
到平面图形体会:从实物图到立体图形,从立体图形到平面图形的过程并掌握其方法。中心投影与平行投影皮影戏表演中心投影与平行投影 我们知道,光是直线传播的.由于光的照射,在不透明
物体后面的屏幕上可以留下这个物体的影子,这种现象
叫做投影.我们把光线叫做投影线,把留下物体影子的
屏幕叫做投影面.生活有许多投影的例子,下面看一个例子----手影中心投影我们把光由一点向外散射形成的投影,叫做中心投影中心投影的投影线交于一点.中心投影现象在我们的日常生活中非常普遍.例如,在电灯泡的照射下,物体后面的屏幕上就会形成
影子,而且随着物体距离灯泡的远近,形成的影子大小
就会有所不同. 人的视觉、照片、美术作品都具有中心投影的特点.平行投影 我们把在一束平行光线照射下形成的投影,叫做
平行投影. 平行投影的投影是平行的,在平行投影中,投影线
正对着投影面时,叫做正投影,否则叫做斜投影. 在平行投影之下,与投影面平行的平面图形留下
的影子,与这个平面图形的形状和大小完全相同的. 下面看看一个三角板在中心投影和不同方向的
平行投影之下,所产生的投影.正投影:投影线与投影面垂直斜投影:投影线与投影面不垂直光源A中心投影平行投影斜投影正投影 我们从不同的方向观察同一个物体时,可能看到不同的图形.为了能完整确切地表达物体的形状和大小,必须从多方面观察物体.在几何中,我们通常选择从正面、上面、左面三个方向观察物体。 这样就把一个立体图形用几个平面图形来描述图2图1 在生活和生产实践中,我们经常需要用从多个方向看到的图形来描述物体的形状和大小,如下图 2 所示就是图 1 所示的热水瓶从不同方向看到的图形.——三视图初步感知三视图的形成OxyzVHW
如图所示, 为了表达物体的形状,往往需要把物体向几个不同平面分别作正投影,通常采用互相垂直的三个投影面,建立一个三面投影体系。三视图的形成 一个投影面正立放置,叫做正立投影面,投影到这个平面内的图形叫做正视图(主视图),即光线从几何体的前面向后面正投影,得到的投影图 三视图的形成 一个投影面水平放置,叫做水平投影面,投影到这个平面的图象叫做俯视图, 即光线从几何体的上面向下面正投影,得到的投影图; 三视图的形成 和正立、水平两个投射面都垂直的投射面叫做侧立投影面,通常把这个平面放在正立投影面的右面,投射到这个平面内的图形叫做侧视图(左视图),即光线从几何体的左面向右面正投影,得到的投影图。正视图、俯视图和侧视图统称为几何体的三视图.俯视图三视图的对应规律 观察:正视图、侧视图和俯视图分别是从几何体的正前方、正左方和正上方观察到的几何体的正投影图,它们都是平面图形。观察长方体的三视图,你能得出同一个几何体的正视图、侧视图和俯视图在形状、大小方面的关系吗?俯视图正
视
图正视图俯视图侧视图a a bbcca bc 一个物体的三视图的排列规则是:俯视图放在正视图的下面,长度与正视图一样,侧视图放在正视图的右面,高度与正视图一样,宽度与俯视图的宽度一样,即
“长对正、高平齐、宽相等”
它是指:正视图和俯视图一样长;正视图和侧视图一样高;俯视图和侧视图一样宽
正视图反映出物体的长和高,俯视图反映出物体的长和宽,侧视图反映出物体的高和宽.三视图的对应规律例 1 画出下列几何体的三视图 从立体图形到平面图形从立体图形到平面图形解: 圆柱的三视图如下: 正视图侧视图俯视图从立体图形到平面图形解: 圆锥的三视图如下: 正视图侧视图俯视图解: 此几何体的三视图如下: 从立体图形到平面图形正视图侧视图俯视图虚实:在画图时,看的见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.注:若相邻的两平面的相交,表面的交线是它们的分界线,在三视图中,分界线和可见轮廓线都用实线画出正三棱锥的三视图正视图俯视图侧视图长对正高平齐宽相等画下面正六棱柱的三视图画下面六棱柱的三视图正视图俯视图侧视图练习 画出正四棱柱、正六棱柱的三视图 从立体图形到平面图形主从立体图形到平面图形解: 正六棱柱的三视图如下: 正视图 侧视图俯视图 正六棱柱正视图 侧视图 俯视图 解: 正六棱柱的三视图如下: 从立体图形到平面图形1.确定正视图方向3.先画出能反映物体真实形
状的一个视图 4.运用
原则画出其它视图5.检查、修正2.布置视图 长对正、高平齐、宽相等注意:俯视图安排在正视图的正下方,侧视图安排在正视图的正右方. 主视图侧视图俯视图三视图的作图步骤 正视图侧视图俯视图注:看得见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.正视图侧视图俯视图从平面图形到立体图形例 2 根据下列的三视图画出几何体简单几何体的三视图下列物体表示的几何体是一些简单几何体的组合
体,你能画出它们的三视图吗?对于简单几何体的组合体,必须认真观察
它的基本结构,然后再画它的三视图.图(1)的几何结构,从上到下分别是圆柱,
圆台和圆柱,它的三视图如左图所示.对于简单组合体同样也要符合三视图的对应规律.简单几何体的三视图知识小结投影平行投影中心投影斜投影正投影1.投影正视图
侧视图
俯视图
画物体的三视图时,要符合如下原则:
位置:正视图 侧视图
俯视图
2.大小:长对正,高平齐,宽相等
3.虚实: 在画图时,看得见部分的轮廓通常画成实线,看不见部分的轮廓线通常画成虚线.知识小结2.三视图——从正面看到的图——从左面看到的图——从上面看到的图复习 在物体的平行投影中, 如果投影线与投影面垂直, 则称这样的平行投影为正投影. 正投影除具有平行投影的性质外, 还有以下性质:
(1)垂直于投影面的直线或线段的正投影是 点 ;
(2)垂直于投影面的平面图形的正投影是 直线
或直线的一部分.1. 中心投影、平行投影、正投影的定义2. 正投影的性质:
正视图——从正面看到的图
侧视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:正视图 侧视图
俯视图
大小:长对正,高平齐,宽相等3.三视图对几何体的三视图, 下列说法正确的是
正视图反映物体的长和宽
俯视图反映物体的长和高
侧视图反映物体的高和宽
正视图反映物体的高和宽2. 一个几何体的三视图如果相同, 那么这个几何体
可能是
A. 长方体 B. 正方体
C. 球 D. 正方体或球练习三视图表达的意义 从前面正对着物体观察,画出正视图,正视图反映了物体的长和高及前后两个面的实形。
从上向下正对着物体观察,画出俯视图,布置在正视图的正下方,俯视图反映了物体的长和宽及上下两个面的实形。
从左向右正对着物体观察,画出侧视图,布置在正视图的正右方,侧视图反映了物体的宽和高及左右两个面的实形。三视图能反映物体真实的形状和长、宽、高 注意:
若相邻两物体的表面相交,表面的交线是它们的边界线. 在三视图中,边界线和可见轮廓线都用实线画出;
在画三视图时,不可见轮廓线用虚线画出
绘制与检查时,应先从整体到局部顺序进行;
先定正视俯视左视方向,同一物体放的位置不同,三视图可能不一样;
观察组合体由哪些基本几何体形成,什么形成方式,交线位置如何.正方形正方形正方形矩形矩形矩形矩形矩形圆圆圆圆圆圆等腰三角形 等腰三角形等腰梯形等腰梯形归纳简单几何体的三视图: 例2 由5个相同的小立方块搭成的几何体如图所示,请画出它的三视图:侧视图俯视图正视图解: 所求三视图如图主视方向上题作如下变化(如图所示),请画出它的三视图:侧视图俯视图正视图解: 所求三视图如图主视方向解: 所求三视图如图: 左图是由七个小正方体组成的物体的俯视图,上面的数字表示这一位置小正方体的个数,你能画出它的另外两个视图吗?俯视图11221主视方向 一个骰子由 1 ~ 6 六个数字组成, 请根据下图A, B, C 三种状态所显示的数字, 推出 “ ? ” 处的数字是( )A. 6 B. 3 C. 1 D. 2A针对性练习1.课后练习 P152.名师一号P9--10 第1, 2, 3, 4, 6, 10题
