人教版九年级数学上册第二十四章 圆 综合测试卷(含答案)
文档属性
| 名称 | 人教版九年级数学上册第二十四章 圆 综合测试卷(含答案) | 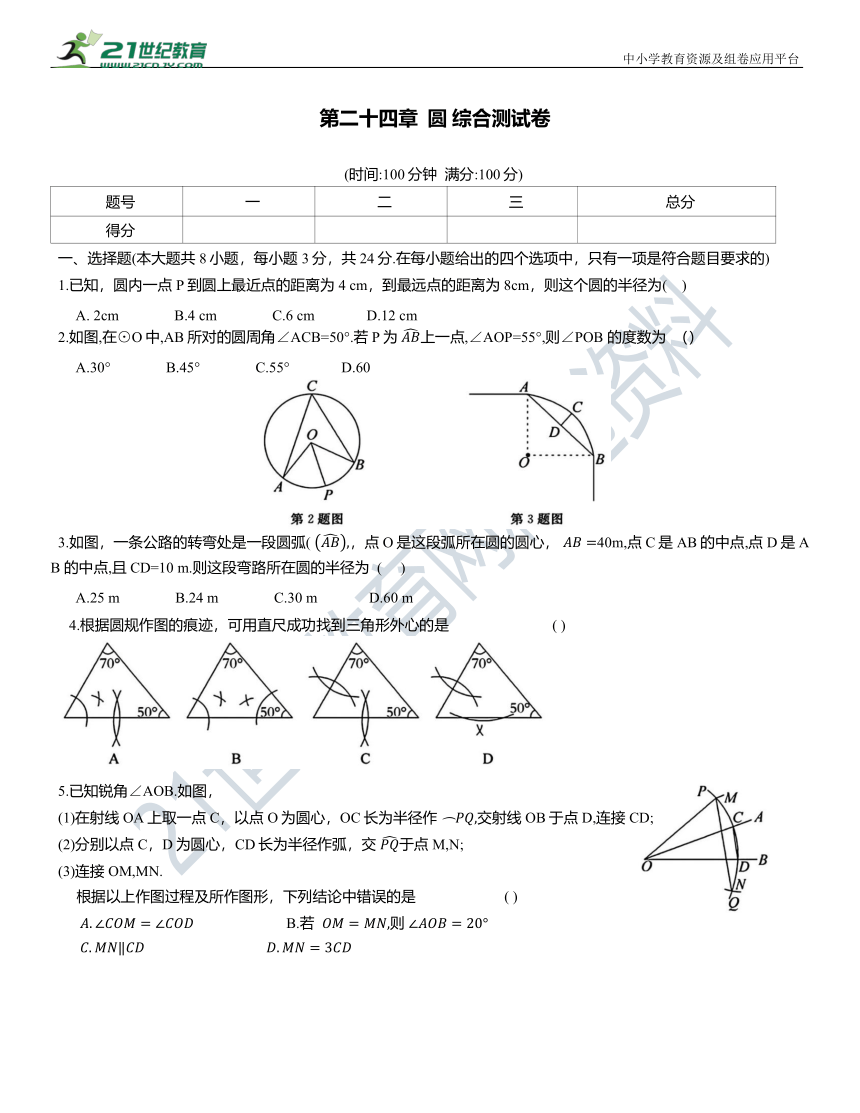 | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 16:27:38 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆 综合测试卷
(时间:100分钟 满分:100分)
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知,圆内一点 P到圆上最近点的距离为 4 cm,到最远点的距离为 8cm,则这个圆的半径为( )
A. 2cm B.4 cm C.6 cm D.12 cm
2.如图,在⊙O中,AB所对的圆周角∠ACB=50°.若P为 上一点,∠AOP=55°,则∠POB 的度数为 ()
A.30° B.45° C.55° D.60
3.如图,一条公路的转弯处是一段圆弧( ,点O是这段弧所在圆的圆心, 40m,点C是AB的中点,点D是AB 的中点,且CD=10 m.则这段弯路所在圆的半径为 ( )
A.25 m B.24 m C.30 m D.60 m
4.根据圆规作图的痕迹,可用直尺成功找到三角形外心的是 ( )
5.已知锐角∠AOB.如图,
(1)在射线OA上取一点C,以点O为圆心,OC长为半径作 交射线 OB于点D,连接 CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;
(3)连接 OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是 ( )
B.若 则
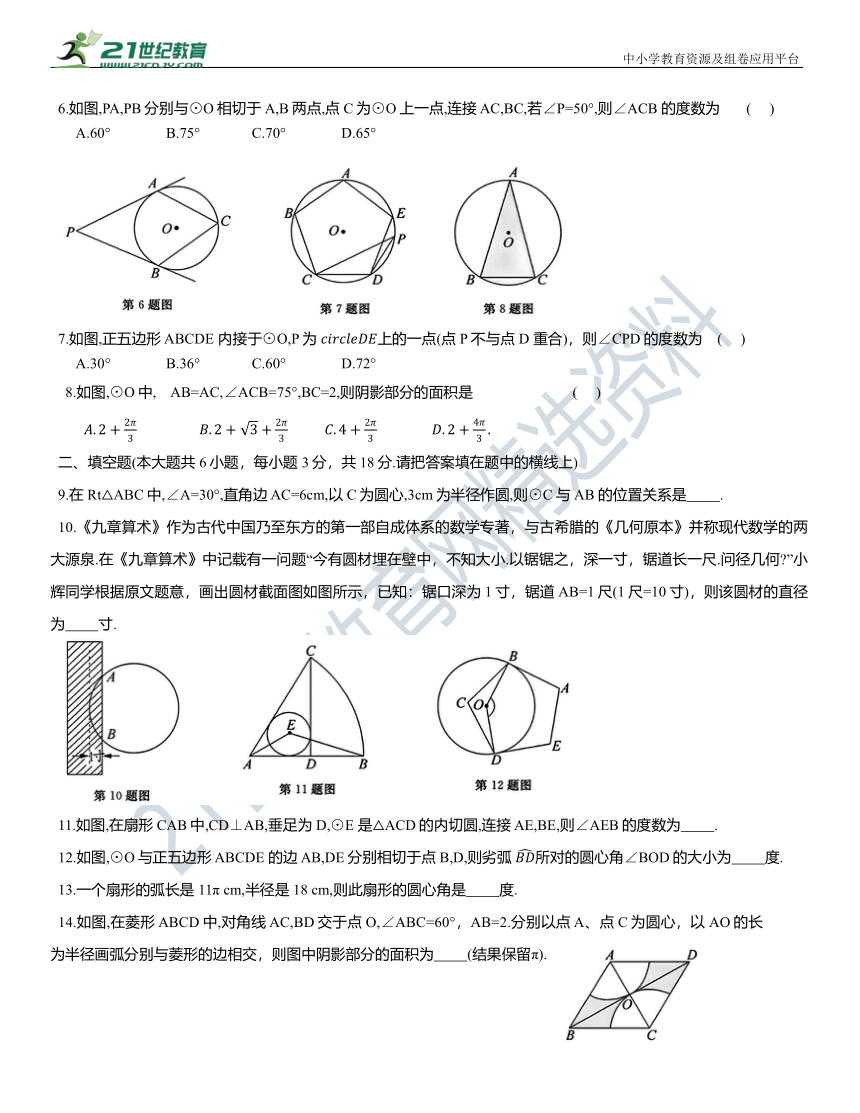
6.如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接 AC,BC,若∠P=50°,则∠ACB 的度数为 ( )
A.60° B.75° C.70° D.65°
7.如图,正五边形 ABCDE 内接于⊙O,P为 上的一点(点 P不与点 D 重合),则∠CPD的度数为 ( )
A.30° B.36° C.60° D.72°
8.如图,⊙O中, AB=AC,∠ACB=75°,BC=2,则阴影部分的面积是 ( )
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)
9.在Rt△ABC中,∠A=30°,直角边 AC=6cm,以C为圆心,3cm为半径作圆,则⊙C与AB 的位置关系是 .
10.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何 ”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为 寸.
11.如图,在扇形CAB中,CD⊥AB,垂足为 D,⊙E 是△ACD的内切圆,连接 AE,BE,则∠AEB的度数为 .
12.如图,⊙O与正五边形 ABCDE 的边 AB,DE分别相切于点B,D,则劣弧 所对的圆心角∠BOD的大小为 度.
13.一个扇形的弧长是 11π cm,半径是 18 cm,则此扇形的圆心角是 度.
14.如图,在菱形 ABCD中,对角线 AC,BD交于点O,∠ABC=60°,AB=2.分别以点 A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为 (结果保留π).
三、解答题(本大题共6小题,共58分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分8分)
如图所示,AB是⊙O的一条弦,( ,垂足为 E,交⊙O于点C、D.
(1)若 求 的度数;
(2)若. 求CD的长.
16.(本小题满分8分)
如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点.
(1)该图中弧所在圆的圆心 D 的坐标为 ;
(2)根据(1)中的条件填空:
①圆D的半径= (结果保留根号);
②点(7,0)在圆 D (填“上”、“内”或“外”);
③求 的长.
17.(本小题满分10分)
如图,在 中, .以AB为直径的半圆O交AC 于点D,点E是 上不与点B,D重合的任意一点,连接 AE交 BD 于点F,连接 BE 并延长交AC 于点G.
(1)求证:
(2)填空:
①若 ,且点 E是 的中点,则 DF 的长为 ;
②取 的中点 H,当 的度数为 时,四边形 OBEH为菱形.
18.(本小题满分 10分)
如图,在△ABC中,∠ACB=90°,CA=CB,点O在△ABC的内部,⊙O经过B,C两点,交AB于点D,连接 CO并延长交AB 于点G,以GD,GC为邻边作平行四边形GDEC.
(1)判断 DE与⊙O 的位置关系,并说明理由;
(2)若点 B是DBCI的中点,⊙O的半径为 2,求 的长.
19.(本小题满分10分)
如图1,正方形 ABCD 内接于⊙O,E为( 上任意一点,连接 DE、AE.
(1)求∠AED 的度数.
(2)如图2,过点 B作BF∥DE交⊙O于点F,连接 AF,AF=1,AE=4,求 DE 的长度.
20.(本小题满分 12分)
如图所示,△ABC是等腰三角形,且AC= BC,∠ACB=120°,在AB上取一点O,使 OB=OC,以O为圆心,OB为半径作圆,过C作CD∥AB交⊙O于点D,连接 BD.
(1)猜想 AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形 BOCD 的形状,并证明你的判断;
(3)已知 AC=6,求扇形OBC所围成的圆锥的底面圆半径r.
第二十四章 综合测试卷
一、1. C 2. B 3. A 4. C 5. D 6. D 7. B 8. A
二、9.相切 10.26 11.135° 12.144 13.110
三、15.(1)∠DOB=52°;(2)CD=8.
16.(1)(2,0) (2)①2 ,②外;(
17.解:(1)证明:∵BA=BC,∠ABC=90°,∴∠CAB=∠C=45°.
∵AB为半圆O 的直径,∴∠ADF=∠BDG=90°,∴∠DBA=∠DAB=45°,
∴AD=BD.∵∠DAF和∠DBG都是 所对的圆周角,
∴∠DAF=∠DBG,∴△ADF≌△BDG.
(2)①4—2 ②30.(注若填为 30°,不扣分)
18.解:(1)DE是⊙O的切线.
证明:连接OD,∵∠ACB=90°,CA=CB,
∴∠ABC=45°,
∴∠COD=2∠ABC=90°,
又∵四边形GDEC是平行四边形,∴DE∥CG,
∴∠EDO+∠COD=180°,∴∠EDO=90°,
∴DE是⊙O的切线.
(2)连接OB,∵点 B是 的中点,
又∵
的长为
答:BC的长为
19.(1)∠AED=45°.
(2)连接CF,CE,CA,BD,作 于H.∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,∴∠ABF=∠CDE,
∴∠CFA=∠AEC=90°,∴∠DEC=∠AFB=135°,
∵CD=AB,∴△CDE≌△ABF,∴AF=CE=1,
∵∠DHE=90°,∴∠HDE=∠HED=45°,∴DH=HE,设 DH=EH=x,
在 Rt△ADH中, 解得 (舍去),
20.解:(1)AC与⊙O 相切.证明如下:∵AC=BC,∠ACB=120°,∴∠A=
∵OB=OC, ∴ ∠OCB=∠OBC=30°,∴∠ACO=∠ACB-∠OCB
∴OC⊥AC,∴AC是⊙O的切线.
(2)四边形 BOCD 为菱形.证明如下:连接OD,∵CD∥AB,∴∠AOC=∠OCD,∵∠AOC=∠OBC+∠OCB=60°,∴∠OCD=60°,而OC=OD,∴△OCD为等边三角形,∴CD=OC=OB,∴四边形 BOCD为平行四边形,
∴四边形 BOCD为菱形.
(3)在 中,
∴弧 BC的长 设圆锥的底面圆半径为 r,则 2πr
第二十四章 圆 综合测试卷
(时间:100分钟 满分:100分)
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知,圆内一点 P到圆上最近点的距离为 4 cm,到最远点的距离为 8cm,则这个圆的半径为( )
A. 2cm B.4 cm C.6 cm D.12 cm
2.如图,在⊙O中,AB所对的圆周角∠ACB=50°.若P为 上一点,∠AOP=55°,则∠POB 的度数为 ()
A.30° B.45° C.55° D.60
3.如图,一条公路的转弯处是一段圆弧( ,点O是这段弧所在圆的圆心, 40m,点C是AB的中点,点D是AB 的中点,且CD=10 m.则这段弯路所在圆的半径为 ( )
A.25 m B.24 m C.30 m D.60 m
4.根据圆规作图的痕迹,可用直尺成功找到三角形外心的是 ( )
5.已知锐角∠AOB.如图,
(1)在射线OA上取一点C,以点O为圆心,OC长为半径作 交射线 OB于点D,连接 CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;
(3)连接 OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是 ( )
B.若 则
6.如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接 AC,BC,若∠P=50°,则∠ACB 的度数为 ( )
A.60° B.75° C.70° D.65°
7.如图,正五边形 ABCDE 内接于⊙O,P为 上的一点(点 P不与点 D 重合),则∠CPD的度数为 ( )
A.30° B.36° C.60° D.72°
8.如图,⊙O中, AB=AC,∠ACB=75°,BC=2,则阴影部分的面积是 ( )
二、填空题(本大题共6小题,每小题3分,共18分.请把答案填在题中的横线上)
9.在Rt△ABC中,∠A=30°,直角边 AC=6cm,以C为圆心,3cm为半径作圆,则⊙C与AB 的位置关系是 .
10.《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何 ”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道AB=1尺(1尺=10寸),则该圆材的直径为 寸.
11.如图,在扇形CAB中,CD⊥AB,垂足为 D,⊙E 是△ACD的内切圆,连接 AE,BE,则∠AEB的度数为 .
12.如图,⊙O与正五边形 ABCDE 的边 AB,DE分别相切于点B,D,则劣弧 所对的圆心角∠BOD的大小为 度.
13.一个扇形的弧长是 11π cm,半径是 18 cm,则此扇形的圆心角是 度.
14.如图,在菱形 ABCD中,对角线 AC,BD交于点O,∠ABC=60°,AB=2.分别以点 A、点C为圆心,以AO的长为半径画弧分别与菱形的边相交,则图中阴影部分的面积为 (结果保留π).
三、解答题(本大题共6小题,共58分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本小题满分8分)
如图所示,AB是⊙O的一条弦,( ,垂足为 E,交⊙O于点C、D.
(1)若 求 的度数;
(2)若. 求CD的长.
16.(本小题满分8分)
如图,网格纸中每个小正方形的边长为1,一段圆弧经过格点.
(1)该图中弧所在圆的圆心 D 的坐标为 ;
(2)根据(1)中的条件填空:
①圆D的半径= (结果保留根号);
②点(7,0)在圆 D (填“上”、“内”或“外”);
③求 的长.
17.(本小题满分10分)
如图,在 中, .以AB为直径的半圆O交AC 于点D,点E是 上不与点B,D重合的任意一点,连接 AE交 BD 于点F,连接 BE 并延长交AC 于点G.
(1)求证:
(2)填空:
①若 ,且点 E是 的中点,则 DF 的长为 ;
②取 的中点 H,当 的度数为 时,四边形 OBEH为菱形.
18.(本小题满分 10分)
如图,在△ABC中,∠ACB=90°,CA=CB,点O在△ABC的内部,⊙O经过B,C两点,交AB于点D,连接 CO并延长交AB 于点G,以GD,GC为邻边作平行四边形GDEC.
(1)判断 DE与⊙O 的位置关系,并说明理由;
(2)若点 B是DBCI的中点,⊙O的半径为 2,求 的长.
19.(本小题满分10分)
如图1,正方形 ABCD 内接于⊙O,E为( 上任意一点,连接 DE、AE.
(1)求∠AED 的度数.
(2)如图2,过点 B作BF∥DE交⊙O于点F,连接 AF,AF=1,AE=4,求 DE 的长度.
20.(本小题满分 12分)
如图所示,△ABC是等腰三角形,且AC= BC,∠ACB=120°,在AB上取一点O,使 OB=OC,以O为圆心,OB为半径作圆,过C作CD∥AB交⊙O于点D,连接 BD.
(1)猜想 AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形 BOCD 的形状,并证明你的判断;
(3)已知 AC=6,求扇形OBC所围成的圆锥的底面圆半径r.
第二十四章 综合测试卷
一、1. C 2. B 3. A 4. C 5. D 6. D 7. B 8. A
二、9.相切 10.26 11.135° 12.144 13.110
三、15.(1)∠DOB=52°;(2)CD=8.
16.(1)(2,0) (2)①2 ,②外;(
17.解:(1)证明:∵BA=BC,∠ABC=90°,∴∠CAB=∠C=45°.
∵AB为半圆O 的直径,∴∠ADF=∠BDG=90°,∴∠DBA=∠DAB=45°,
∴AD=BD.∵∠DAF和∠DBG都是 所对的圆周角,
∴∠DAF=∠DBG,∴△ADF≌△BDG.
(2)①4—2 ②30.(注若填为 30°,不扣分)
18.解:(1)DE是⊙O的切线.
证明:连接OD,∵∠ACB=90°,CA=CB,
∴∠ABC=45°,
∴∠COD=2∠ABC=90°,
又∵四边形GDEC是平行四边形,∴DE∥CG,
∴∠EDO+∠COD=180°,∴∠EDO=90°,
∴DE是⊙O的切线.
(2)连接OB,∵点 B是 的中点,
又∵
的长为
答:BC的长为
19.(1)∠AED=45°.
(2)连接CF,CE,CA,BD,作 于H.∵BF∥DE,AB∥CD,
∴∠BDE=∠DBF,∠BDC=∠ABD,∴∠ABF=∠CDE,
∴∠CFA=∠AEC=90°,∴∠DEC=∠AFB=135°,
∵CD=AB,∴△CDE≌△ABF,∴AF=CE=1,
∵∠DHE=90°,∴∠HDE=∠HED=45°,∴DH=HE,设 DH=EH=x,
在 Rt△ADH中, 解得 (舍去),
20.解:(1)AC与⊙O 相切.证明如下:∵AC=BC,∠ACB=120°,∴∠A=
∵OB=OC, ∴ ∠OCB=∠OBC=30°,∴∠ACO=∠ACB-∠OCB
∴OC⊥AC,∴AC是⊙O的切线.
(2)四边形 BOCD 为菱形.证明如下:连接OD,∵CD∥AB,∴∠AOC=∠OCD,∵∠AOC=∠OBC+∠OCB=60°,∴∠OCD=60°,而OC=OD,∴△OCD为等边三角形,∴CD=OC=OB,∴四边形 BOCD为平行四边形,
∴四边形 BOCD为菱形.
(3)在 中,
∴弧 BC的长 设圆锥的底面圆半径为 r,则 2πr
同课章节目录
