人教版九年级数学上册第二十四章 圆基础复习卷(一)(24.1)(含答案)
文档属性
| 名称 | 人教版九年级数学上册第二十四章 圆基础复习卷(一)(24.1)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 11:37:51 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第二十四章 圆 基础复习卷(一)(24.1)
知识点一 圆的有关概念
1.自行车车轮要做成圆形,实际上是根据圆的以下哪个特征 ( )
A.圆是轴对称图形 B.圆是中心对称图形
C.圆上各点到圆心的距离相等 D.直径是圆中最长的弦
2.下列说法正确的是 ( )
A.弦是直径 B.弧是半圆 C半圆是弧 D.优弧大于劣弧
知识点二 圆的简单计算与证明
3.如图所示,AB是圆O的直径,D是弦AC 的中点,若OD=4,则 BC= .
4.如图,AB是⊙O的直径,C 是 BA 延长线上一点,点 D 在⊙O上,且CD=OA,CD的延长线交⊙O于点E.若 则 的度数为 .
5.如图所示,AB,AC是⊙A的半径,D,E分别是AB,AC的中点.求证BE=CD.
知识点三 垂径定理及其推论
6.如图,⊙O 的直径为 10,AB 为弦,( 垂足为C,若( 则弦AB 的长为 ( )
A.8 B.6 C.4 D.10
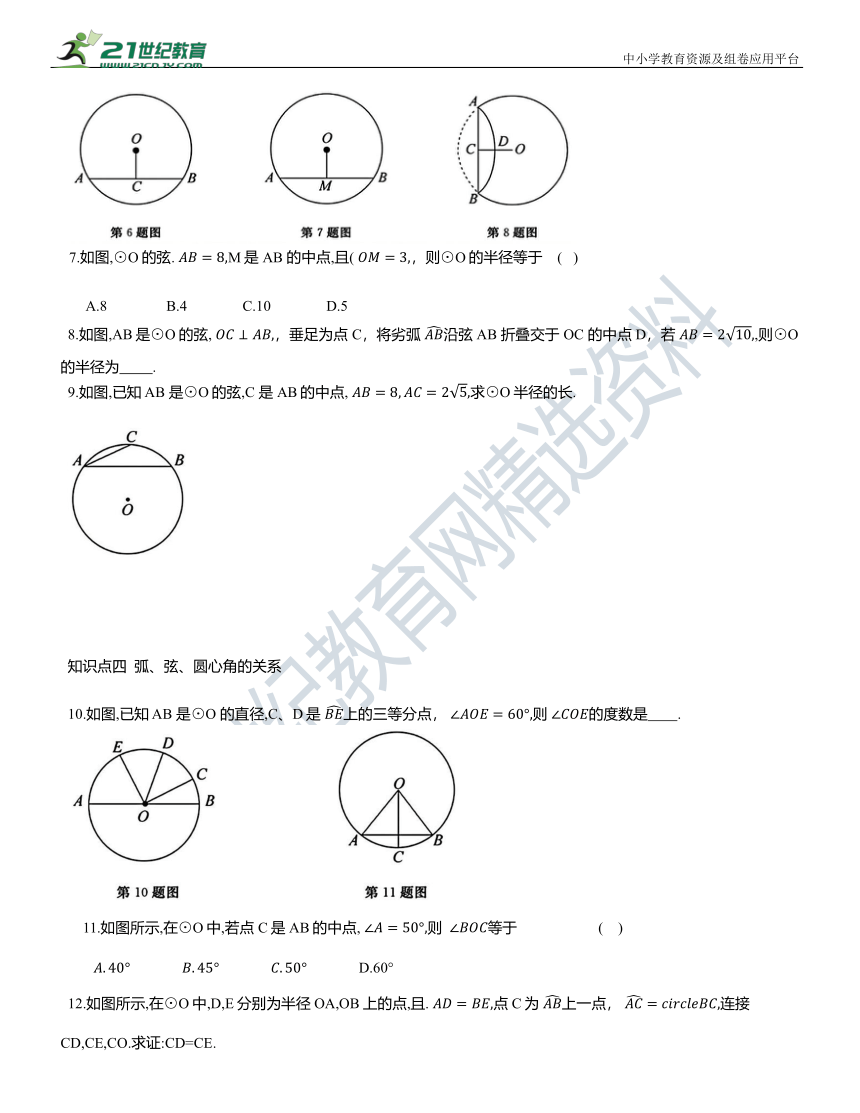
7.如图,⊙O的弦. M是AB 的中点,且( ,则⊙O的半径等于 ( )
A.8 B.4 C.10 D.5
8.如图,AB是⊙O的弦, ,垂足为点 C,将劣弧 沿弦AB 折叠交于 OC 的中点D,若 ,则⊙O的半径为 .
9.如图,已知 AB 是⊙O的弦,C 是AB的中点, 求⊙O半径的长.
知识点四 弧、弦、圆心角的关系
10.如图,已知 AB 是⊙O 的直径,C、D是 上的三等分点, 则 的度数是 .
11.如图所示,在⊙O中,若点 C是AB的中点, 则 等于 ( )
D.60°
12.如图所示,在⊙O中,D,E分别为半径OA,OB上的点,且. 点C为 上一点, 连接 CD,CE,CO.求证:CD=CE.
知识点五 圆周角定理及推论
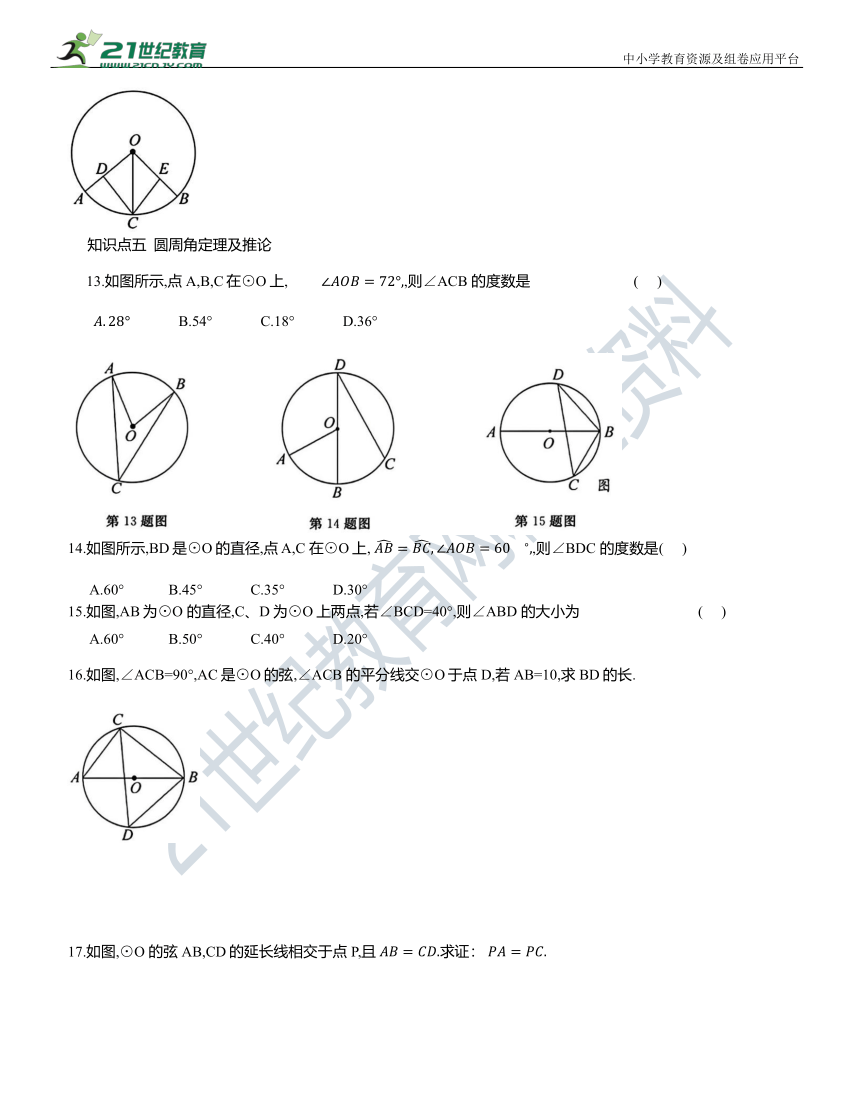
13.如图所示,点A,B,C在⊙O上, ,则∠ACB 的度数是 ( )
B.54° C.18° D.36°
14.如图所示,BD是⊙O的直径,点 A,C 在⊙O上, ,则∠BDC 的度数是( )
A.60° B.45° C.35° D.30°
15.如图,AB为⊙O 的直径,C、D为⊙O上两点,若∠BCD=40°,则∠ABD 的大小为 ( )
A.60° B.50° C.40° D.20°
16.如图,∠ACB=90°,AC是⊙O的弦,∠ACB 的平分线交⊙O于点D,若AB=10,求BD的长.
17.如图,⊙O 的弦AB,CD的延长线相交于点P,且 求证:
知识点六 圆内接四边形的性质
18.如图所示,若四边形 ABCD 是⊙O的内接四边形, 则 的度数是 .
19.如图,四边形 ABCD 内接于⊙O, 交CB 的延长线于点E,若 BA 平分 则 ( )
A.3
20.如图所示,四边形 ABCD 内接于⊙O,点E在对角线AC上,
(1)若 求 的度数;
(2)求证:∠1=∠2.
知识点七 与圆的性质有关的计算与证明
21.如图,AB是⊙O 的直径,点 C为 的中点,CF为⊙O的弦,且 ,垂足为E,连接 BD交CF 于点G,连接CD,AD,BF.
(1)求证:
(2)若 ,求 BF 的长.
1. C 2. C 3.8 4.60° 5.略 6. A 7. D 8.3
9.解:如图,连接OA,连接OC交AB 于 D.设⊙O的半径为r.∵
在 中,
在 中,
解得 r=5.∴⊙O的半径长为 5.
10.80° 11. A 12.略 13. D 14. D 15. B 16.5
17.如图,连接 AC.
即
∴∠C=∠A,
∴PA=PC.
18.110° 19. D
20.(1)78°
(2)证明:∵EC=BC,∴∠CBE=∠CEB.∵∠CBE=∠1+∠CBD,∠CEB=∠2+∠BAC,∴∠1+∠CBD=∠2+∠BAC.∵∠BAC=∠CBD,∴∠1=∠2.
21.解:(1)证明:连接 BC.
∵∠BDC 与∠CFB 都是BC对应的圆周角,∴∠BDC=∠CFB.
∵点C是BD的中点,∴BC=CD.
又直径AB垂直弦CF,∴AB垂直平分线段CF,∴BC=BF,∴CD=BF.
又∠CGD=∠BGF,∴△BFG≌△CDG(AAS).
(2)连接 AC,过点C作AD 延长线的垂线,垂足为 H.∵点C是BD的中点,∴∠HAC=∠BAC,即AC为∠BAD的平分线.
∵CH⊥AD,CE⊥AB,∴CH=CE,
在 Rt△ACE和 Rt△ACH 中,AC=AC,∴△ACE≌△ACH(HL),∴AH=AE.
又在 Rt△CDH 和 Rt△CBE中,BC=CD,CH=CE,
∴△CDH≌△CBE(HL),∴DH=BE=2.
∴AE=AH=AD+DH=2+2=4,∴AB=AE+BE=4+2=6.
∴⊙O 的半径为 3.
连接OC,∴OC=3,∵BE=2,∴OE=OB-BE=3-2=1,
∴在 Rt△COE中,
在 Rt△BEF中,
第二十四章 圆 基础复习卷(一)(24.1)
知识点一 圆的有关概念
1.自行车车轮要做成圆形,实际上是根据圆的以下哪个特征 ( )
A.圆是轴对称图形 B.圆是中心对称图形
C.圆上各点到圆心的距离相等 D.直径是圆中最长的弦
2.下列说法正确的是 ( )
A.弦是直径 B.弧是半圆 C半圆是弧 D.优弧大于劣弧
知识点二 圆的简单计算与证明
3.如图所示,AB是圆O的直径,D是弦AC 的中点,若OD=4,则 BC= .
4.如图,AB是⊙O的直径,C 是 BA 延长线上一点,点 D 在⊙O上,且CD=OA,CD的延长线交⊙O于点E.若 则 的度数为 .
5.如图所示,AB,AC是⊙A的半径,D,E分别是AB,AC的中点.求证BE=CD.
知识点三 垂径定理及其推论
6.如图,⊙O 的直径为 10,AB 为弦,( 垂足为C,若( 则弦AB 的长为 ( )
A.8 B.6 C.4 D.10
7.如图,⊙O的弦. M是AB 的中点,且( ,则⊙O的半径等于 ( )
A.8 B.4 C.10 D.5
8.如图,AB是⊙O的弦, ,垂足为点 C,将劣弧 沿弦AB 折叠交于 OC 的中点D,若 ,则⊙O的半径为 .
9.如图,已知 AB 是⊙O的弦,C 是AB的中点, 求⊙O半径的长.
知识点四 弧、弦、圆心角的关系
10.如图,已知 AB 是⊙O 的直径,C、D是 上的三等分点, 则 的度数是 .
11.如图所示,在⊙O中,若点 C是AB的中点, 则 等于 ( )
D.60°
12.如图所示,在⊙O中,D,E分别为半径OA,OB上的点,且. 点C为 上一点, 连接 CD,CE,CO.求证:CD=CE.
知识点五 圆周角定理及推论
13.如图所示,点A,B,C在⊙O上, ,则∠ACB 的度数是 ( )
B.54° C.18° D.36°
14.如图所示,BD是⊙O的直径,点 A,C 在⊙O上, ,则∠BDC 的度数是( )
A.60° B.45° C.35° D.30°
15.如图,AB为⊙O 的直径,C、D为⊙O上两点,若∠BCD=40°,则∠ABD 的大小为 ( )
A.60° B.50° C.40° D.20°
16.如图,∠ACB=90°,AC是⊙O的弦,∠ACB 的平分线交⊙O于点D,若AB=10,求BD的长.
17.如图,⊙O 的弦AB,CD的延长线相交于点P,且 求证:
知识点六 圆内接四边形的性质
18.如图所示,若四边形 ABCD 是⊙O的内接四边形, 则 的度数是 .
19.如图,四边形 ABCD 内接于⊙O, 交CB 的延长线于点E,若 BA 平分 则 ( )
A.3
20.如图所示,四边形 ABCD 内接于⊙O,点E在对角线AC上,
(1)若 求 的度数;
(2)求证:∠1=∠2.
知识点七 与圆的性质有关的计算与证明
21.如图,AB是⊙O 的直径,点 C为 的中点,CF为⊙O的弦,且 ,垂足为E,连接 BD交CF 于点G,连接CD,AD,BF.
(1)求证:
(2)若 ,求 BF 的长.
1. C 2. C 3.8 4.60° 5.略 6. A 7. D 8.3
9.解:如图,连接OA,连接OC交AB 于 D.设⊙O的半径为r.∵
在 中,
在 中,
解得 r=5.∴⊙O的半径长为 5.
10.80° 11. A 12.略 13. D 14. D 15. B 16.5
17.如图,连接 AC.
即
∴∠C=∠A,
∴PA=PC.
18.110° 19. D
20.(1)78°
(2)证明:∵EC=BC,∴∠CBE=∠CEB.∵∠CBE=∠1+∠CBD,∠CEB=∠2+∠BAC,∴∠1+∠CBD=∠2+∠BAC.∵∠BAC=∠CBD,∴∠1=∠2.
21.解:(1)证明:连接 BC.
∵∠BDC 与∠CFB 都是BC对应的圆周角,∴∠BDC=∠CFB.
∵点C是BD的中点,∴BC=CD.
又直径AB垂直弦CF,∴AB垂直平分线段CF,∴BC=BF,∴CD=BF.
又∠CGD=∠BGF,∴△BFG≌△CDG(AAS).
(2)连接 AC,过点C作AD 延长线的垂线,垂足为 H.∵点C是BD的中点,∴∠HAC=∠BAC,即AC为∠BAD的平分线.
∵CH⊥AD,CE⊥AB,∴CH=CE,
在 Rt△ACE和 Rt△ACH 中,AC=AC,∴△ACE≌△ACH(HL),∴AH=AE.
又在 Rt△CDH 和 Rt△CBE中,BC=CD,CH=CE,
∴△CDH≌△CBE(HL),∴DH=BE=2.
∴AE=AH=AD+DH=2+2=4,∴AB=AE+BE=4+2=6.
∴⊙O 的半径为 3.
连接OC,∴OC=3,∵BE=2,∴OE=OB-BE=3-2=1,
∴在 Rt△COE中,
在 Rt△BEF中,
同课章节目录
