冀教版九年级上册期中测试数学卷(含答案)
文档属性
| 名称 | 冀教版九年级上册期中测试数学卷(含答案) | 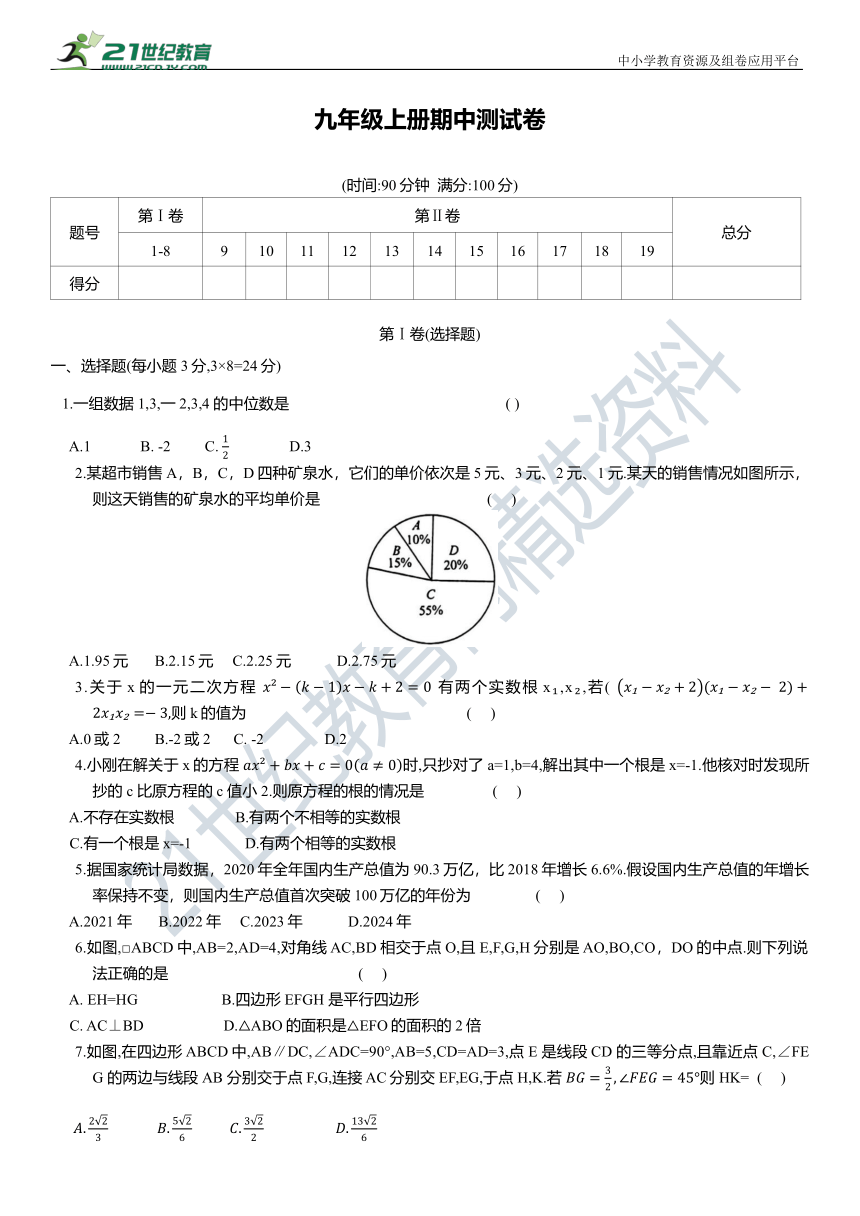 | |
| 格式 | docx | ||
| 文件大小 | 773.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 11:43:54 | ||
图片预览


文档简介
九年级上册期中测试卷
(时间:90分钟 满分:100分)
题号 第Ⅰ卷 第Ⅱ卷 总分
1-8 9 10 11 12 13 14 15 16 17 18 19
得分
第Ⅰ卷(选择题)
一、选择题(每小题3分,3×8=24分)
1.一组数据1,3,一2,3,4 的中位数是 ( )
A.1 B. -2 C. D.3
2.某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是 ( )
A.1.95元 B.2.15元 C.2.25元 D.2.75元
3.关于x的一元二次方程 有两个实数根x ,x ,若( 则 k的值为 ( )
A.0或2 B.-2或2 C. -2 D.2
4.小刚在解关于x的方程 时,只抄对了 a=1,b=4,解出其中一个根是x=-1.他核对时发现所抄的c 比原方程的c 值小2.则原方程的根的情况是 ( )
A.不存在实数根 B.有两个不相等的实数根
C.有一个根是x=-1 D.有两个相等的实数根
5.据国家统计局数据,2020年全年国内生产总值为90.3万亿,比2018年增长6.6%.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破100万亿的年份为 ( )
A.2021年 B.2022年 C.2023年 D.2024年
6.如图,□ABCD中,AB=2,AD=4,对角线 AC,BD相交于点O,且E,F,G,H分别是 AO,BO,CO,DO的中点.则下列说法正确的是 ( )
A. EH=HG B.四边形 EFGH 是平行四边形
C. AC⊥BD D.△ABO的面积是△EFO的面积的2倍
7.如图,在四边形 ABCD中,AB∥DC,∠ADC=90°,AB=5,CD=AD=3,点E 是线段CD 的三等分点,且靠近点 C,∠FEG 的两边与线段AB 分别交于点F,G,连接 AC分别交EF,EG,于点 H,K.若 则 HK= ( )
8.如图,正方形 ABCD的边长为2,点 E是 BC 的中点,AE 与BD 交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接 PN,则以下结论中:
正确的是 ( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(每小题4分,4×6=24分)
9.若关于x的一元二次方程 有实数根,则k 的取值范围是 .
10.甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 参赛人数 平均数 中位数 方差
甲 45 83 85 82
乙 45 83 84 135
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分≥85分为优秀);
③甲班成绩的波动比乙班小.
上述结论中正确的是 .(填写所有正确结论的序号)
11.已知 x ,x 是关于x的一元二次方程. 的两个实数根,且 则k的值为 .
12.如图,把某矩形纸片 ABCD沿EF,GH折叠(点E,H在 AD 边上,点F,G在BC 边上),使点B和点C落在AD 边上同一点P 处,A点的对称点为A′点,D点的对称点为 点.若 90°,△A'EP 的面积为4,△D'PH 的面积为 1,则矩形 ABCD的面积等于 .
13.如图,是小李设计用手电来测量某古城墙高度的示意图,点 P 处放一水平的平面镜,光线从点 A出发经平面镜反射后刚好射到古城墙 CD 的顶端C处,已知 且测得 1.1米,BP=1.9米,PD=19米,那么该古城墙CD的高度是 米.
14.如图,在 Rt△ABC中,∠ABC=90°,BC=3,D为斜边AC 的中点,连接 BD,F是BC边上的动点(不与点 B,C重合),过点 B 作BE⊥BD交DF 延长线于点E,连接 CE.下列结论:
中小学教育资源及组卷应用平台
①若 BF=CF,则
②若∠BDE=∠BAC,AB=4,则
③△ABD和△CBE一定相似;
④若∠A=30°,∠BCE=90°,则
其中正确的是 .(填写所有正确结论的序号)
三、解答题(共52分,解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分10分)为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动,为了解九年级 500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图,请根据图表信息解答以下问题:
知识竞赛成绩分组统计表
组别 分数/分 频数
A 60≤x<70 a
B 70≤x<80 10
C 80≤x<90 14
D 90≤x<100 18
(1)本次调查一共随机抽取了 个参赛学生的成绩;
(2)表中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有 人.
16.(本小题满分 10分)关于x的一元二次方程 的两个实数根分别为.
(1)求m 的取值范围;
(2)若 求m 的值.
17.(本小题满分10分)沧州市某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是
18.(本小题满分10分)随着粤港澳大湾区建设的加速推进,广东省正加速布局以 5G 等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约 1.5万座,计划到 2020年底,全省 5G 基站数量是目前的4倍;到2022年底,全省5G基站数量将达到17.34万座.
(1)计划到2020年底,全省 5G基站的数量是多少万座
(2)按照计划,求2020年底至 2022年底,全省 5G基站数量的年平均增长率.
19.(本小题满分 12分)如图,在矩形 ABCD中, AC为对角线,点 P 沿 AB边从点 A 开始向点 B 以2cm /s的速度移动,点Q沿 DA 边从点 D 开始向点 A 以 的速度移动,如果 P,Q同时出发,用ts表示移动的时间(
(1)当t为何值时, 为等腰直角三角形
(2)求四边形 QAPC的面积,提出一个与计算结果相关的结论;
(3)直接写出当t为何值时, 与 相似.
一、1一5 DCDAB 6-8 BBA
二、9. k≤1且 k≠0 10.①②③ 11. ﹣2 13.1114.①②④
三、15.解:(1)50 (2)8 (3)C (4)320
16.(1)∵方程有两个实数根,∴Δ≥0,∴9-4×1×(m-1)≥0,解得 又∵2(x +x )+x x +10=0,∴2×(-3)+m-1+10=0,∴m=-3
17.设矩形温室的宽为xm,则长为 2xm,根据题意得( =288,∴2(x-2) =288,∴(x-2) =144,∴x-2=±12,解得x =-10(不合题意,舍去), 所以 . 答:当矩形温室的长为 28 m,宽为 14 m 时,蔬菜种植的面积是
18.解:(1)1.5×4=6(万座)答:到2020年底,全省5G基站的数量是6万座.(2)设全省 5G基站数量的年平均增长率为x,则( 17.34,解得 (舍去).答:2020年底至2022年底,全省 5G基站数量的年平均增长率为 70%.
19.(1)若△QAP为等腰直角三角形,则只需 根据题干条件知AQ=(6-t) cm,AP=2t cm,列方程得( 解得 即当t=2s时,△AQP为等腰直角三角形
(2)四边形 QAPC的面积=矩形ABCD的面积—三角形 CDQ的面积一三角形 PBC的面积,设( ,根据题干条件可得四边形 QAPC的面积 ,故可得结论四边形 QAPC的面积是矩形ABCD 面积的一半
(3)当t=3s或1.2s时,△PAQ与△ABC相似
(时间:90分钟 满分:100分)
题号 第Ⅰ卷 第Ⅱ卷 总分
1-8 9 10 11 12 13 14 15 16 17 18 19
得分
第Ⅰ卷(选择题)
一、选择题(每小题3分,3×8=24分)
1.一组数据1,3,一2,3,4 的中位数是 ( )
A.1 B. -2 C. D.3
2.某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是 ( )
A.1.95元 B.2.15元 C.2.25元 D.2.75元
3.关于x的一元二次方程 有两个实数根x ,x ,若( 则 k的值为 ( )
A.0或2 B.-2或2 C. -2 D.2
4.小刚在解关于x的方程 时,只抄对了 a=1,b=4,解出其中一个根是x=-1.他核对时发现所抄的c 比原方程的c 值小2.则原方程的根的情况是 ( )
A.不存在实数根 B.有两个不相等的实数根
C.有一个根是x=-1 D.有两个相等的实数根
5.据国家统计局数据,2020年全年国内生产总值为90.3万亿,比2018年增长6.6%.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破100万亿的年份为 ( )
A.2021年 B.2022年 C.2023年 D.2024年
6.如图,□ABCD中,AB=2,AD=4,对角线 AC,BD相交于点O,且E,F,G,H分别是 AO,BO,CO,DO的中点.则下列说法正确的是 ( )
A. EH=HG B.四边形 EFGH 是平行四边形
C. AC⊥BD D.△ABO的面积是△EFO的面积的2倍
7.如图,在四边形 ABCD中,AB∥DC,∠ADC=90°,AB=5,CD=AD=3,点E 是线段CD 的三等分点,且靠近点 C,∠FEG 的两边与线段AB 分别交于点F,G,连接 AC分别交EF,EG,于点 H,K.若 则 HK= ( )
8.如图,正方形 ABCD的边长为2,点 E是 BC 的中点,AE 与BD 交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接 PN,则以下结论中:
正确的是 ( )
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(每小题4分,4×6=24分)
9.若关于x的一元二次方程 有实数根,则k 的取值范围是 .
10.甲、乙两班举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
班级 参赛人数 平均数 中位数 方差
甲 45 83 85 82
乙 45 83 84 135
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛得分≥85分为优秀);
③甲班成绩的波动比乙班小.
上述结论中正确的是 .(填写所有正确结论的序号)
11.已知 x ,x 是关于x的一元二次方程. 的两个实数根,且 则k的值为 .
12.如图,把某矩形纸片 ABCD沿EF,GH折叠(点E,H在 AD 边上,点F,G在BC 边上),使点B和点C落在AD 边上同一点P 处,A点的对称点为A′点,D点的对称点为 点.若 90°,△A'EP 的面积为4,△D'PH 的面积为 1,则矩形 ABCD的面积等于 .
13.如图,是小李设计用手电来测量某古城墙高度的示意图,点 P 处放一水平的平面镜,光线从点 A出发经平面镜反射后刚好射到古城墙 CD 的顶端C处,已知 且测得 1.1米,BP=1.9米,PD=19米,那么该古城墙CD的高度是 米.
14.如图,在 Rt△ABC中,∠ABC=90°,BC=3,D为斜边AC 的中点,连接 BD,F是BC边上的动点(不与点 B,C重合),过点 B 作BE⊥BD交DF 延长线于点E,连接 CE.下列结论:
中小学教育资源及组卷应用平台
①若 BF=CF,则
②若∠BDE=∠BAC,AB=4,则
③△ABD和△CBE一定相似;
④若∠A=30°,∠BCE=90°,则
其中正确的是 .(填写所有正确结论的序号)
三、解答题(共52分,解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分10分)为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动,为了解九年级 500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图,请根据图表信息解答以下问题:
知识竞赛成绩分组统计表
组别 分数/分 频数
A 60≤x<70 a
B 70≤x<80 10
C 80≤x<90 14
D 90≤x<100 18
(1)本次调查一共随机抽取了 个参赛学生的成绩;
(2)表中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有 人.
16.(本小题满分 10分)关于x的一元二次方程 的两个实数根分别为.
(1)求m 的取值范围;
(2)若 求m 的值.
17.(本小题满分10分)沧州市某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是
18.(本小题满分10分)随着粤港澳大湾区建设的加速推进,广东省正加速布局以 5G 等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约 1.5万座,计划到 2020年底,全省 5G 基站数量是目前的4倍;到2022年底,全省5G基站数量将达到17.34万座.
(1)计划到2020年底,全省 5G基站的数量是多少万座
(2)按照计划,求2020年底至 2022年底,全省 5G基站数量的年平均增长率.
19.(本小题满分 12分)如图,在矩形 ABCD中, AC为对角线,点 P 沿 AB边从点 A 开始向点 B 以2cm /s的速度移动,点Q沿 DA 边从点 D 开始向点 A 以 的速度移动,如果 P,Q同时出发,用ts表示移动的时间(
(1)当t为何值时, 为等腰直角三角形
(2)求四边形 QAPC的面积,提出一个与计算结果相关的结论;
(3)直接写出当t为何值时, 与 相似.
一、1一5 DCDAB 6-8 BBA
二、9. k≤1且 k≠0 10.①②③ 11. ﹣2 13.1114.①②④
三、15.解:(1)50 (2)8 (3)C (4)320
16.(1)∵方程有两个实数根,∴Δ≥0,∴9-4×1×(m-1)≥0,解得 又∵2(x +x )+x x +10=0,∴2×(-3)+m-1+10=0,∴m=-3
17.设矩形温室的宽为xm,则长为 2xm,根据题意得( =288,∴2(x-2) =288,∴(x-2) =144,∴x-2=±12,解得x =-10(不合题意,舍去), 所以 . 答:当矩形温室的长为 28 m,宽为 14 m 时,蔬菜种植的面积是
18.解:(1)1.5×4=6(万座)答:到2020年底,全省5G基站的数量是6万座.(2)设全省 5G基站数量的年平均增长率为x,则( 17.34,解得 (舍去).答:2020年底至2022年底,全省 5G基站数量的年平均增长率为 70%.
19.(1)若△QAP为等腰直角三角形,则只需 根据题干条件知AQ=(6-t) cm,AP=2t cm,列方程得( 解得 即当t=2s时,△AQP为等腰直角三角形
(2)四边形 QAPC的面积=矩形ABCD的面积—三角形 CDQ的面积一三角形 PBC的面积,设( ,根据题干条件可得四边形 QAPC的面积 ,故可得结论四边形 QAPC的面积是矩形ABCD 面积的一半
(3)当t=3s或1.2s时,△PAQ与△ABC相似
同课章节目录
