2023-2024学年人教版第一学期八年级数学第11章《三角形》单元综合训练(无答案)
文档属性
| 名称 | 2023-2024学年人教版第一学期八年级数学第11章《三角形》单元综合训练(无答案) | 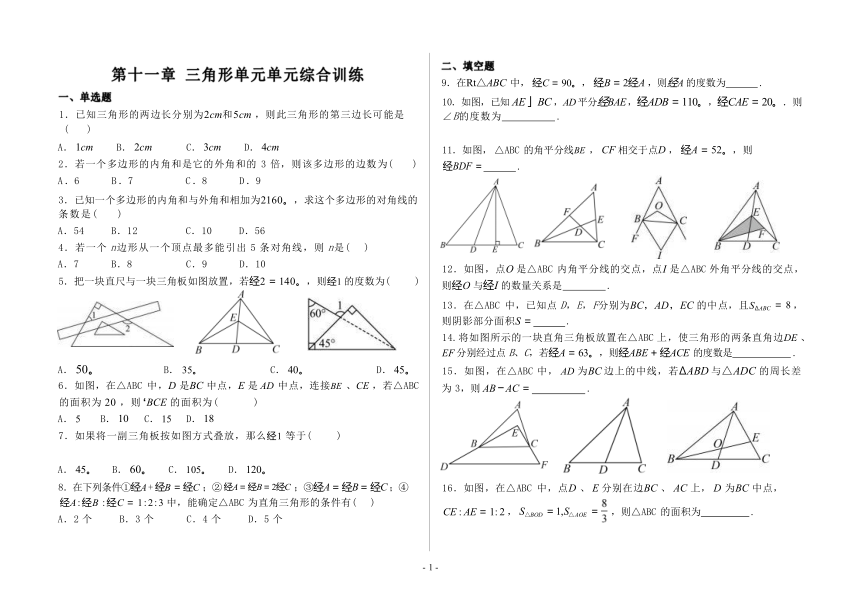 | |
| 格式 | docx | ||
| 文件大小 | 89.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 14:10:38 | ||
图片预览

文档简介
- 1 -
第十一章 三角形单元单元综合训练
一、单选题
1.已知三角形的两边长分别为2cm和5cm ,则此三角形的第三边长可能是 ( )
A. 1cm B. 2cm C. 3cm D. 4cm
2.若一个多边形的内角和是它的外角和的 3 倍,则该多边形的边数为( )
A .6 B .7 C .8 D .9
3.已知一个多边形的内角和与外角和相加为2160。,求这个多边形的对角线的 条数是( )
A.54 B.12 C.10 D.56
4.若一个 n边形从一个顶点最多能引出 5 条对角线,则 n是( )
A.7 B.8 C.9 D.10
5.把一块直尺与一块三角板如图放置,若经2 = 140。,则经1 的度数为( )
A. 50。 B. 35。 C. 40。 D. 45。
6.如图,在△ABC 中,D 是BC 中点,E 是 AD 中点,连接BE 、CE ,若△ABC
的面积为 20 ,则 ‘BCE 的面积为( )
A. 5 B. 10 C. 15 D. 18
7.如果将一副三角板按如图方式叠放,那么经1 等于( )
A. 45。 B. 60。 C. 105。 D. 120。
8.在下列条件①经A + 经B = 经C ;② 经A = 经B = 2经C ;③经A = 经B = 经C ;④ 经A:经B :经C = 1:2:3 中,能确定△ABC 为直角三角形的条件有( )
A.2 个 B.3 个 C.4 个 D.5 个
二、填空题
9.在Rt△ABC 中, 经C = 90。, 经B = 2经A ,则经A 的度数为 .
10.如图,已知 AE 」BC ,AD 平分经BAE ,经ADB = 110。,经CAE = 20。.则 ∠B的度数为 .
11.如图, △ABC 的角平分线BE , CF 相交于点D , 经A = 52。,则
经BDF = .
12.如图,点O 是△ABC 内角平分线的交点,点I 是△ABC 外角平分线的交点, 则经O 与经I 的数量关系是 .
13.在△ABC 中,已知点 D,E,F分别为BC,AD,EC 的中点,且SΔABC = 8 , 则阴影部分面积S = .
14.将如图所示的一块直角三角板放置在△ABC 上,使三角形的两条直角边DE 、 EF 分别经过点 B、C,若经A = 63。,则经ABE + 经ACE 的度数是 . 15.如图,在△ABC 中, AD 为BC 边上的中线,若ΔABD 与△ADC 的周长差
为 3,则 AB 一 AC = .
16.如图,在△ABC 中,点D 、 E 分别在边BC 、 AC 上, D 为BC 中点,
CE : AE = 1: 2 , S△BOD = 1, S△AOE = ,则△ABC 的面积为 .
- 2 -
三、解答题
17.如图,在△ABC 中,AD BC 于点 D,AE 平分BAC ,1 = 30。,2 = 20。, 求 B 的度数.
18.在各个内角都相等的多边形中,一个内角等于一个外角的 5 倍,求这个多 边形每一个内角的度数和它的边数.
19.在△ABC 中, CD 平分ACB 交AB 于点D , AH 是△ABC 边BC 上的高, 且 ACB = 70。, ADC = 80。,求 BAH 的度数.
20.如图,在△DBC 中, BD CD ,BA 平分DBC 交CD 边于点 A, BAC = 124。,求C 的度数.
21.如图, CD,CE 分别是△ABC 的高和中线,若 AC=7cm,BC=24cm,AB=25cm, ACB = 90。. (1)求CD 的长; (2)求△BCE 与△ACE 的周长差.
22.如图,在△ABC 中,BD, CE 分别是 AC, AB 上的高,H 是BD, CE 交点. (1)若A = 60。,求BHC 的度数. (2)若BHC = 3A ,求 A 的度数.
23.如图,在△ABC 中, AD 平分BAC ,P 为线段 AD 上的一点,过点P 作 PE AD 交直线BC 于点E .
(1)若B = 40。, ACB = 80。,求 E 的度数;
(2)若B = 34。, E = 30。,求ACB 的度数;
(3)请根据以上结果,直接写出 E 与 B , ACB 之间的数量关系.
第十一章 三角形单元单元综合训练
一、单选题
1.已知三角形的两边长分别为2cm和5cm ,则此三角形的第三边长可能是 ( )
A. 1cm B. 2cm C. 3cm D. 4cm
2.若一个多边形的内角和是它的外角和的 3 倍,则该多边形的边数为( )
A .6 B .7 C .8 D .9
3.已知一个多边形的内角和与外角和相加为2160。,求这个多边形的对角线的 条数是( )
A.54 B.12 C.10 D.56
4.若一个 n边形从一个顶点最多能引出 5 条对角线,则 n是( )
A.7 B.8 C.9 D.10
5.把一块直尺与一块三角板如图放置,若经2 = 140。,则经1 的度数为( )
A. 50。 B. 35。 C. 40。 D. 45。
6.如图,在△ABC 中,D 是BC 中点,E 是 AD 中点,连接BE 、CE ,若△ABC
的面积为 20 ,则 ‘BCE 的面积为( )
A. 5 B. 10 C. 15 D. 18
7.如果将一副三角板按如图方式叠放,那么经1 等于( )
A. 45。 B. 60。 C. 105。 D. 120。
8.在下列条件①经A + 经B = 经C ;② 经A = 经B = 2经C ;③经A = 经B = 经C ;④ 经A:经B :经C = 1:2:3 中,能确定△ABC 为直角三角形的条件有( )
A.2 个 B.3 个 C.4 个 D.5 个
二、填空题
9.在Rt△ABC 中, 经C = 90。, 经B = 2经A ,则经A 的度数为 .
10.如图,已知 AE 」BC ,AD 平分经BAE ,经ADB = 110。,经CAE = 20。.则 ∠B的度数为 .
11.如图, △ABC 的角平分线BE , CF 相交于点D , 经A = 52。,则
经BDF = .
12.如图,点O 是△ABC 内角平分线的交点,点I 是△ABC 外角平分线的交点, 则经O 与经I 的数量关系是 .
13.在△ABC 中,已知点 D,E,F分别为BC,AD,EC 的中点,且SΔABC = 8 , 则阴影部分面积S = .
14.将如图所示的一块直角三角板放置在△ABC 上,使三角形的两条直角边DE 、 EF 分别经过点 B、C,若经A = 63。,则经ABE + 经ACE 的度数是 . 15.如图,在△ABC 中, AD 为BC 边上的中线,若ΔABD 与△ADC 的周长差
为 3,则 AB 一 AC = .
16.如图,在△ABC 中,点D 、 E 分别在边BC 、 AC 上, D 为BC 中点,
CE : AE = 1: 2 , S△BOD = 1, S△AOE = ,则△ABC 的面积为 .
- 2 -
三、解答题
17.如图,在△ABC 中,AD BC 于点 D,AE 平分BAC ,1 = 30。,2 = 20。, 求 B 的度数.
18.在各个内角都相等的多边形中,一个内角等于一个外角的 5 倍,求这个多 边形每一个内角的度数和它的边数.
19.在△ABC 中, CD 平分ACB 交AB 于点D , AH 是△ABC 边BC 上的高, 且 ACB = 70。, ADC = 80。,求 BAH 的度数.
20.如图,在△DBC 中, BD CD ,BA 平分DBC 交CD 边于点 A, BAC = 124。,求C 的度数.
21.如图, CD,CE 分别是△ABC 的高和中线,若 AC=7cm,BC=24cm,AB=25cm, ACB = 90。. (1)求CD 的长; (2)求△BCE 与△ACE 的周长差.
22.如图,在△ABC 中,BD, CE 分别是 AC, AB 上的高,H 是BD, CE 交点. (1)若A = 60。,求BHC 的度数. (2)若BHC = 3A ,求 A 的度数.
23.如图,在△ABC 中, AD 平分BAC ,P 为线段 AD 上的一点,过点P 作 PE AD 交直线BC 于点E .
(1)若B = 40。, ACB = 80。,求 E 的度数;
(2)若B = 34。, E = 30。,求ACB 的度数;
(3)请根据以上结果,直接写出 E 与 B , ACB 之间的数量关系.
