3.1 从算式到方程(第2课时)课件(共25张PPT)-2023-2024学年七年级数学上册同步备课系列(人教版)
文档属性
| 名称 | 3.1 从算式到方程(第2课时)课件(共25张PPT)-2023-2024学年七年级数学上册同步备课系列(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 07:03:31 | ||
图片预览







文档简介
新课导入
讲授新课
当堂检测
课堂小结
第三章 一元一次方程
3.1 从算式到方程
3.1.2 等式的性质
情景引入
情景引入1
法律天平象征着公平与正义
天平是一种比较有形物体重量差异的仪器,如果两边重量稍有不等,就会偏斜;法院是对无形行为评判、对是非明辨的部门,要求公正不阿,如果有私心或被权力金钱所左右,也就会让庄严的法律失去平衡。
由于以天平作为公正的标识,那么在审理案件时,法官就能很好地运用天平原理操作了。在现行的法律天平中,法官普遍运用了天平原理进行权衡,且确保了其准确性,两边孰轻孰重,法律的天平一下子就获得了结果,也让旁人一看就明白谁是谁非。
情景引入2
思考:要让天平平衡应该满足什么条件?
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.
知识点一 等式的概念
知识精讲
√
√
√
√
√
2.下列各式中哪些是等式?
用等号表示相等关系的式子叫做等式. 我们可以用a=b表示一般的等式.
1.什么是等式?
知识点二 等式的性质
知识精讲
想一想:将手边的物品用小天平称量,试着找出质量相等的物品.
知识精讲
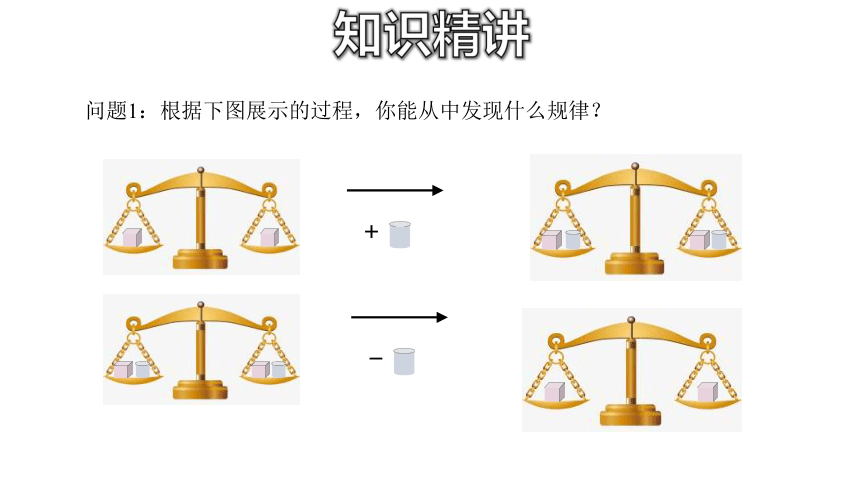
问题1:根据下图展示的过程,你能从中发现什么规律?
+
-
知识精讲
概念归纳
我们可以发现,平衡的天平两边同时都加(或减)相同的量,天平还保持平衡.
等式性质1:
等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式 即
如果a=b,那么a+c=b+c,a-c=b-c.
知识精讲
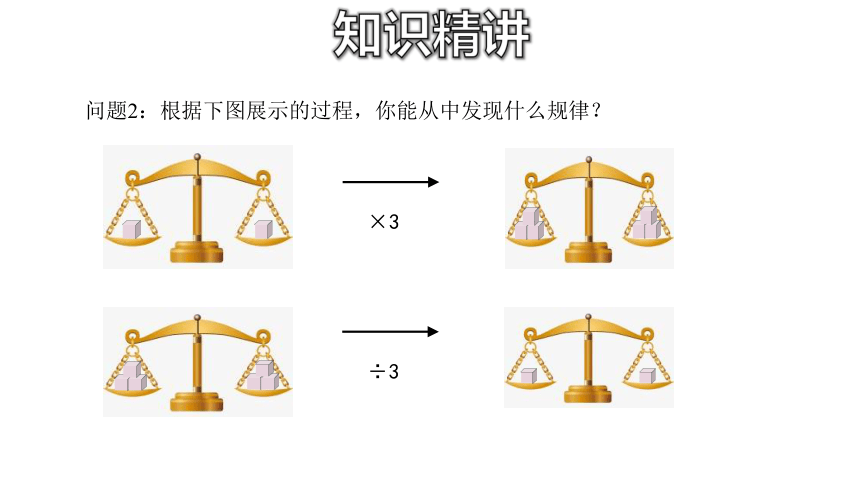
问题2:根据下图展示的过程,你能从中发现什么规律?
×3
÷3
知识精讲
等式的两边乘以(或除以)同一个数(除数不能为0),所得结果仍是等式.
等式性质2:
若a=b,则ac=______
bc
若a=b(c≠0),则
c
c
典型例题
典例精析
【例1】填空,并说明理由.
(1)如果a+2 = b+7,那么a= ;
解:因为a+2=b+7 ,由等式性质1可知,
等式两边都减去2,得
a + 2 - 2 = b + 7 -2,
即 a = b + 5 .
(2)如果3x = 9y,那么 x= ;
解:因为3x=9y,由等式性质2可知,
等式两边都除以3,得
,
即 x = 3y.
b + 5
3y
(3)如果 ,那么3a= .
解:因为 ,由等式性质2可知,
等式两边都乘6,得
即 3a = 2b .
2b
练一练
1.下列选项中,不能由已知等式a=b推出的是( )
A.a+3x=b+3x B.a-2=b-2 C.ac=bc D.????????=????????
2.下列变形一定正确的是( )
A.由x=y,得x+2=y-2 B.由x=y,得2x-1=2y-1
C.由x=y+1,得2x=2y+1 D.由x2=y2,得x=y
3.用适当的数或式子填空,使所得的结果仍是等式,并说明变形的依据和过程.
(1)若3x+5=8,则3x=8-____,依据是___________,等式的两边________;
?
D
B
5
等式的性质1
减5
(2)若-4x=14,则x=______,依据是_______________,等式的两边________
__________;
(3)若2m-3n=7,则2m=7+____,依据是_______________,等式的两边______.
?
-????????????
?
等式的性质2
除以-4
(乘以-????????)
?
3n
等式的性质1
加3n
知识点三 利用等式的性质解方程
知识精讲
思考:利用等式的性质解下列方程:
(1) x + 15= 26
解:
得
方程两边同时减去15,
x + 15 = 26
-15
-15
于是 =
x
11
小结:解一元一次方程要“化归”为“ x=a ”的形式.
知识精讲
两边同时除以-5,
得
解:
方程
(2) -5x = 20
思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ?
化简,得
x=-4
-5x÷(-5)= 20 ÷(-5)
典型例题
典例精析
【例2】利用等式的性质解下列方程:
(1)x+5=-7; (2)0.4x=-2; (3)12x-6=-9; (4)3x-2=5x+6.
?
解:(1)两边减5,得x+5-5=-7-5.于是x=-12.
(2)两边除以0.4,得0.4????0.4=?20.4.于是x=-5.
(3)两边加6,得12x-6+6=-9+6.化简,得12x=-3.两边乘2,得x=-6.
(4)两边减5x,得3x-2-5x=5x+6-5x.化简,得-2x-2=6.
两边加2,得-2x-2+2=6+2.化简,得-2x=8.
两边除以-2,得x=-4.
?
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
方程的左右两边相等,所以x=-4是原方程的解.
例如(4)3x-2=5x+6.将x=-4分别代入方程的左、右两边
左边=3×(-4)-2=-14;右边=5×(-4)+6=-14.
练一练
解:(1)两边减2,得2+3x-2=-x+6-2.
化简,得3x=-x+4.
两边加x,得3x+x=-x+4+x.
化简,得4x=4.
两边除以4,得x=1.
检验:将x=1代入方程2+3x=-x+6的左边,得2+3x1=5.将x=1代入方程2+3x=-x+6的右边,得-1+6=5.方程的左右两边相等,所以x=l是方程2+3x=-x+6的解.
1、利用等式的性质解下列.方程并检验:
(1)2+3x=-x+6; (2)-????3=3; (3)56x-13=14; (4)-????2-3=5.
?
(2)两边乘-3,得y=-9.
检验:将y=-9代入方程-????3=3的左边,得-?93=3.
方程的左右两边相等y
所以y=-9是方程-????3=3的解.
?
(3)两边加13,得56x-13+13=14+13.
化简,得56x=712.两边乘65,得x=710.
检验:将x=710代入方程56x-13=14的左边, 得76×710-13=14.
方程的左右两边相等, 所以x=710是方程56x-13=14的解.
?
(4)两边加3,得-????2-3+3=5+3.
化简,得-????2=8.
两边乘-2,得a=-16.
检验:将a=-16代入方程-????2-3=5的左边,得-?162-3=5.
方程的左右两边相等,所以a=-16是方程-????2-3=5的解.
?
课堂练习
(2) 怎样从等式 3+x=1 得到等式 x=-2?
(3) 怎样从等式 4x=12 得到等式 x=3?
(4) 怎样从等式 得到等式 a=b?
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
1、 (1) 怎样从等式 x-5= y-5 得到等式 x = y ?
依据等式的性质1两边同时加5.
2、己知2x2-x=5,求多项式-4x2+2x-8的值.
解:等式两边乘-2,得-2(2x2-x)=5×(-2).
化简,得-4x2+2x=-10.
两边减8,得-4x2+2x-8=-10-8=-18.
3、利用等式的性质解方程:
(1)7+x=-3;
(2)-3x=27;
解:两边减7得
解:两边除以-3得
两边除以2得
-3x÷(-3)=27÷(-3)
x=-10
解:两边加6得
2x-6+6=10+6
x=8.
(3)2x-6=10.
7+x-7=-3-7
x=-9
2x=16
2x÷2=16÷2
4. 已知关于x的方程 和方程3x -10 =5的解相同,求m的值.
解:方程3x-10 =5的解为x =5,
将其代入方程
得到 ,
解得m =2.
课堂总结
等式的
基本性质
基本性质1
基本性质2
应用
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
运用等式的性质把方程“化归”为最简的形式 x = a
讲授新课
当堂检测
课堂小结
第三章 一元一次方程
3.1 从算式到方程
3.1.2 等式的性质
情景引入
情景引入1
法律天平象征着公平与正义
天平是一种比较有形物体重量差异的仪器,如果两边重量稍有不等,就会偏斜;法院是对无形行为评判、对是非明辨的部门,要求公正不阿,如果有私心或被权力金钱所左右,也就会让庄严的法律失去平衡。
由于以天平作为公正的标识,那么在审理案件时,法官就能很好地运用天平原理操作了。在现行的法律天平中,法官普遍运用了天平原理进行权衡,且确保了其准确性,两边孰轻孰重,法律的天平一下子就获得了结果,也让旁人一看就明白谁是谁非。
情景引入2
思考:要让天平平衡应该满足什么条件?
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡.
知识点一 等式的概念
知识精讲
√
√
√
√
√
2.下列各式中哪些是等式?
用等号表示相等关系的式子叫做等式. 我们可以用a=b表示一般的等式.
1.什么是等式?
知识点二 等式的性质
知识精讲
想一想:将手边的物品用小天平称量,试着找出质量相等的物品.
知识精讲
问题1:根据下图展示的过程,你能从中发现什么规律?
+
-
知识精讲
概念归纳
我们可以发现,平衡的天平两边同时都加(或减)相同的量,天平还保持平衡.
等式性质1:
等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式 即
如果a=b,那么a+c=b+c,a-c=b-c.
知识精讲
问题2:根据下图展示的过程,你能从中发现什么规律?
×3
÷3
知识精讲
等式的两边乘以(或除以)同一个数(除数不能为0),所得结果仍是等式.
等式性质2:
若a=b,则ac=______
bc
若a=b(c≠0),则
c
c
典型例题
典例精析
【例1】填空,并说明理由.
(1)如果a+2 = b+7,那么a= ;
解:因为a+2=b+7 ,由等式性质1可知,
等式两边都减去2,得
a + 2 - 2 = b + 7 -2,
即 a = b + 5 .
(2)如果3x = 9y,那么 x= ;
解:因为3x=9y,由等式性质2可知,
等式两边都除以3,得
,
即 x = 3y.
b + 5
3y
(3)如果 ,那么3a= .
解:因为 ,由等式性质2可知,
等式两边都乘6,得
即 3a = 2b .
2b
练一练
1.下列选项中,不能由已知等式a=b推出的是( )
A.a+3x=b+3x B.a-2=b-2 C.ac=bc D.????????=????????
2.下列变形一定正确的是( )
A.由x=y,得x+2=y-2 B.由x=y,得2x-1=2y-1
C.由x=y+1,得2x=2y+1 D.由x2=y2,得x=y
3.用适当的数或式子填空,使所得的结果仍是等式,并说明变形的依据和过程.
(1)若3x+5=8,则3x=8-____,依据是___________,等式的两边________;
?
D
B
5
等式的性质1
减5
(2)若-4x=14,则x=______,依据是_______________,等式的两边________
__________;
(3)若2m-3n=7,则2m=7+____,依据是_______________,等式的两边______.
?
-????????????
?
等式的性质2
除以-4
(乘以-????????)
?
3n
等式的性质1
加3n
知识点三 利用等式的性质解方程
知识精讲
思考:利用等式的性质解下列方程:
(1) x + 15= 26
解:
得
方程两边同时减去15,
x + 15 = 26
-15
-15
于是 =
x
11
小结:解一元一次方程要“化归”为“ x=a ”的形式.
知识精讲
两边同时除以-5,
得
解:
方程
(2) -5x = 20
思考:为使 (2) 中未知项的系数化为1,将要用到等式的什么性质 ?
化简,得
x=-4
-5x÷(-5)= 20 ÷(-5)
典型例题
典例精析
【例2】利用等式的性质解下列方程:
(1)x+5=-7; (2)0.4x=-2; (3)12x-6=-9; (4)3x-2=5x+6.
?
解:(1)两边减5,得x+5-5=-7-5.于是x=-12.
(2)两边除以0.4,得0.4????0.4=?20.4.于是x=-5.
(3)两边加6,得12x-6+6=-9+6.化简,得12x=-3.两边乘2,得x=-6.
(4)两边减5x,得3x-2-5x=5x+6-5x.化简,得-2x-2=6.
两边加2,得-2x-2+2=6+2.化简,得-2x=8.
两边除以-2,得x=-4.
?
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
方程的左右两边相等,所以x=-4是原方程的解.
例如(4)3x-2=5x+6.将x=-4分别代入方程的左、右两边
左边=3×(-4)-2=-14;右边=5×(-4)+6=-14.
练一练
解:(1)两边减2,得2+3x-2=-x+6-2.
化简,得3x=-x+4.
两边加x,得3x+x=-x+4+x.
化简,得4x=4.
两边除以4,得x=1.
检验:将x=1代入方程2+3x=-x+6的左边,得2+3x1=5.将x=1代入方程2+3x=-x+6的右边,得-1+6=5.方程的左右两边相等,所以x=l是方程2+3x=-x+6的解.
1、利用等式的性质解下列.方程并检验:
(1)2+3x=-x+6; (2)-????3=3; (3)56x-13=14; (4)-????2-3=5.
?
(2)两边乘-3,得y=-9.
检验:将y=-9代入方程-????3=3的左边,得-?93=3.
方程的左右两边相等y
所以y=-9是方程-????3=3的解.
?
(3)两边加13,得56x-13+13=14+13.
化简,得56x=712.两边乘65,得x=710.
检验:将x=710代入方程56x-13=14的左边, 得76×710-13=14.
方程的左右两边相等, 所以x=710是方程56x-13=14的解.
?
(4)两边加3,得-????2-3+3=5+3.
化简,得-????2=8.
两边乘-2,得a=-16.
检验:将a=-16代入方程-????2-3=5的左边,得-?162-3=5.
方程的左右两边相等,所以a=-16是方程-????2-3=5的解.
?
课堂练习
(2) 怎样从等式 3+x=1 得到等式 x=-2?
(3) 怎样从等式 4x=12 得到等式 x=3?
(4) 怎样从等式 得到等式 a=b?
依据等式的性质1两边同时减3.
依据等式的性质2两边同时除以4或同乘 .
依据等式的性质2两边同时除以 或同乘100.
1、 (1) 怎样从等式 x-5= y-5 得到等式 x = y ?
依据等式的性质1两边同时加5.
2、己知2x2-x=5,求多项式-4x2+2x-8的值.
解:等式两边乘-2,得-2(2x2-x)=5×(-2).
化简,得-4x2+2x=-10.
两边减8,得-4x2+2x-8=-10-8=-18.
3、利用等式的性质解方程:
(1)7+x=-3;
(2)-3x=27;
解:两边减7得
解:两边除以-3得
两边除以2得
-3x÷(-3)=27÷(-3)
x=-10
解:两边加6得
2x-6+6=10+6
x=8.
(3)2x-6=10.
7+x-7=-3-7
x=-9
2x=16
2x÷2=16÷2
4. 已知关于x的方程 和方程3x -10 =5的解相同,求m的值.
解:方程3x-10 =5的解为x =5,
将其代入方程
得到 ,
解得m =2.
课堂总结
等式的
基本性质
基本性质1
基本性质2
应用
如果a=b,那么a±c=b±c.
如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .
运用等式的性质把方程“化归”为最简的形式 x = a
