3.1 勾股定理同步练习(无答案) 2023-2024学年苏科版八年级数学上册
文档属性
| 名称 | 3.1 勾股定理同步练习(无答案) 2023-2024学年苏科版八年级数学上册 | 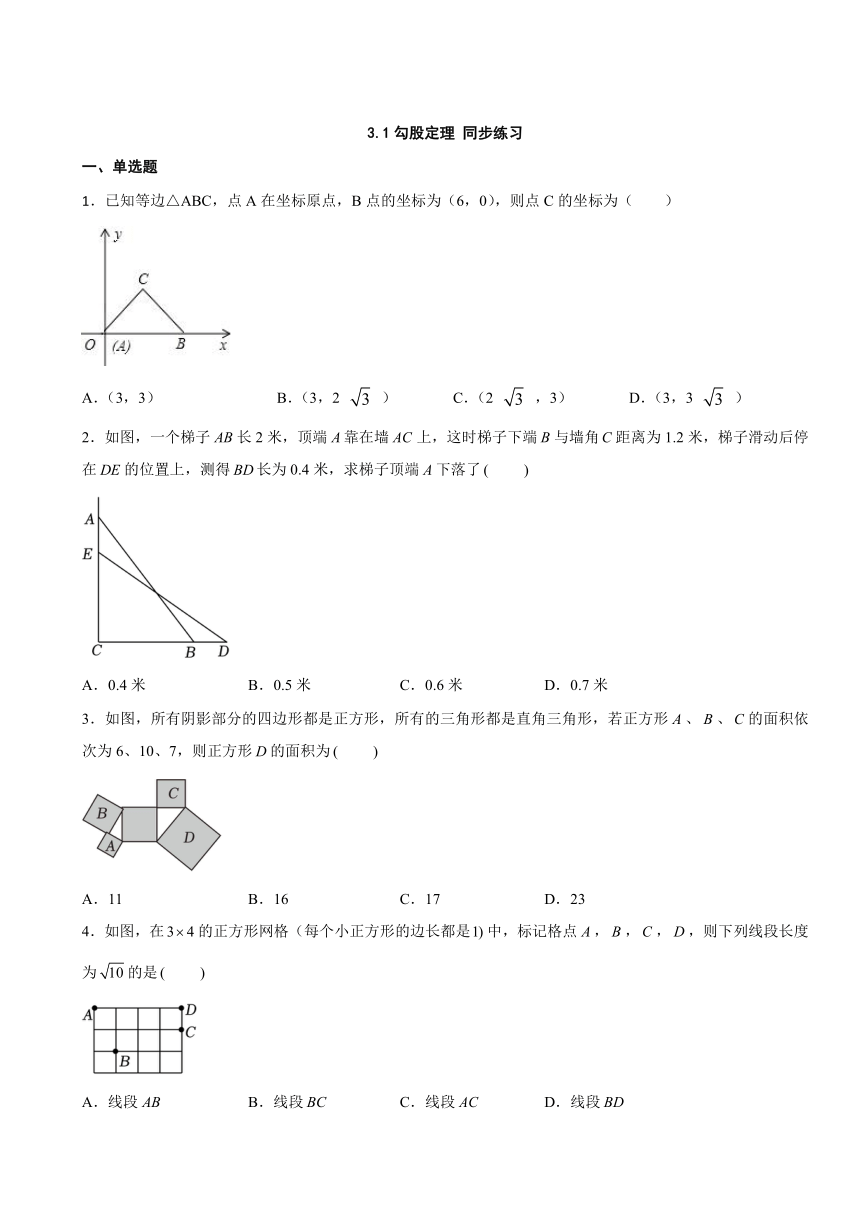 | |
| 格式 | docx | ||
| 文件大小 | 445.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 13:05:15 | ||
图片预览


文档简介
3.1勾股定理 同步练习
一、单选题
1.已知等边△ABC,点A在坐标原点,B点的坐标为(6,0),则点C的坐标为( )
A.(3,3) B.(3,2 ) C.(2 ,3) D.(3,3 )
2.如图,一个梯子长2米,顶端靠在墙上,这时梯子下端与墙角距离为1.2米,梯子滑动后停在的位置上,测得长为0.4米,求梯子顶端下落了
A.0.4米 B.0.5米 C.0.6米 D.0.7米
3.如图,所有阴影部分的四边形都是正方形,所有的三角形都是直角三角形,若正方形、、的面积依次为6、10、7,则正方形的面积为
A.11 B.16 C.17 D.23
4.如图,在的正方形网格(每个小正方形的边长都是中,标记格点,,,,则下列线段长度为的是
A.线段 B.线段 C.线段 D.线段
5.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
6.在 中, , , ,若以点C为圆心,r为半径的 与直线 相切,则r的值为( )
A.2.4 B.3 C.4.8 D.5
7. 如图,在正方形中,点在上,点在的延长线上满足,连接,取的中点,连接,,若,则( )
A.
A. B. C.
8.如图,在Rt△ABC中,点D,E分别是边AC、AB上的两点,连接BD,CE,CD=AE,已知BC=6,AB=8,则BD+CE的最小值是( )
A. B.10 C.9.6 D.5+
二、填空题
1.一个直角三角形的两条直角边的长分别为5cm和12cm,则斜边长为 cm。
2.如图,在中,,,,平分交于点,于点,则线段的长度为 .
3.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是 .
4.如图,中,分别以这个三角形的三边为边长作正方形,面积分别记为、、.如果,则阴影部分的面积为 .
5.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线、交于点若,,则______.
三、解答题
1.如图,将放置在直角坐标系中,B、C分别是斜边DE和直角边OE上的点,把用沿着线段BC折叠,点E的对应点为,若点落在DO的中点上,求OC的长.
2在如图所示的方格图中,每个小方格的边长均为1,则的周长为多少?
3.如图1,放在墙角的立柜的上下底面是等腰直角三角形,如图2所示,若腰长为1m,现要将这个立柜搬过宽为0.8m的通道,你觉得能通过吗?请说明理由.
4.(1)问题发现:如图,和均为等边三角形,当旋转至点,,在同一直线上,连接.填空:
①的度数为 ;
②线段、之间的数量关系是 .
(2)拓展研究:如图,和均为等腰三角形,且,点、、在同一直线上,若,,,求、、之间的数量关系.
(3)探究发现:(1)题中图中的和,在旋转过程中当点,,不在同一直线上时,设直线与相交于点,试在备用图中探索的度数,直接写出结果,不必说明理由.
一、单选题
1.已知等边△ABC,点A在坐标原点,B点的坐标为(6,0),则点C的坐标为( )
A.(3,3) B.(3,2 ) C.(2 ,3) D.(3,3 )
2.如图,一个梯子长2米,顶端靠在墙上,这时梯子下端与墙角距离为1.2米,梯子滑动后停在的位置上,测得长为0.4米,求梯子顶端下落了
A.0.4米 B.0.5米 C.0.6米 D.0.7米
3.如图,所有阴影部分的四边形都是正方形,所有的三角形都是直角三角形,若正方形、、的面积依次为6、10、7,则正方形的面积为
A.11 B.16 C.17 D.23
4.如图,在的正方形网格(每个小正方形的边长都是中,标记格点,,,,则下列线段长度为的是
A.线段 B.线段 C.线段 D.线段
5.如图,在边长为1个单位长度的小正方形组成的网格中,点A、B都是格点,则线段AB的长度为( )
A.5 B.6 C.7 D.25
6.在 中, , , ,若以点C为圆心,r为半径的 与直线 相切,则r的值为( )
A.2.4 B.3 C.4.8 D.5
7. 如图,在正方形中,点在上,点在的延长线上满足,连接,取的中点,连接,,若,则( )
A.
A. B. C.
8.如图,在Rt△ABC中,点D,E分别是边AC、AB上的两点,连接BD,CE,CD=AE,已知BC=6,AB=8,则BD+CE的最小值是( )
A. B.10 C.9.6 D.5+
二、填空题
1.一个直角三角形的两条直角边的长分别为5cm和12cm,则斜边长为 cm。
2.如图,在中,,,,平分交于点,于点,则线段的长度为 .
3.如图,在中,,,.以为一条边向三角形外部作正方形,则正方形的面积是 .
4.如图,中,分别以这个三角形的三边为边长作正方形,面积分别记为、、.如果,则阴影部分的面积为 .
5.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形,对角线、交于点若,,则______.
三、解答题
1.如图,将放置在直角坐标系中,B、C分别是斜边DE和直角边OE上的点,把用沿着线段BC折叠,点E的对应点为,若点落在DO的中点上,求OC的长.
2在如图所示的方格图中,每个小方格的边长均为1,则的周长为多少?
3.如图1,放在墙角的立柜的上下底面是等腰直角三角形,如图2所示,若腰长为1m,现要将这个立柜搬过宽为0.8m的通道,你觉得能通过吗?请说明理由.
4.(1)问题发现:如图,和均为等边三角形,当旋转至点,,在同一直线上,连接.填空:
①的度数为 ;
②线段、之间的数量关系是 .
(2)拓展研究:如图,和均为等腰三角形,且,点、、在同一直线上,若,,,求、、之间的数量关系.
(3)探究发现:(1)题中图中的和,在旋转过程中当点,,不在同一直线上时,设直线与相交于点,试在备用图中探索的度数,直接写出结果,不必说明理由.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
