第二十三章 旋转 单元练习 (含答案)2023—2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十三章 旋转 单元练习 (含答案)2023—2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 123.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 13:10:03 | ||
图片预览


文档简介
第二十三章 旋转
一、选择题
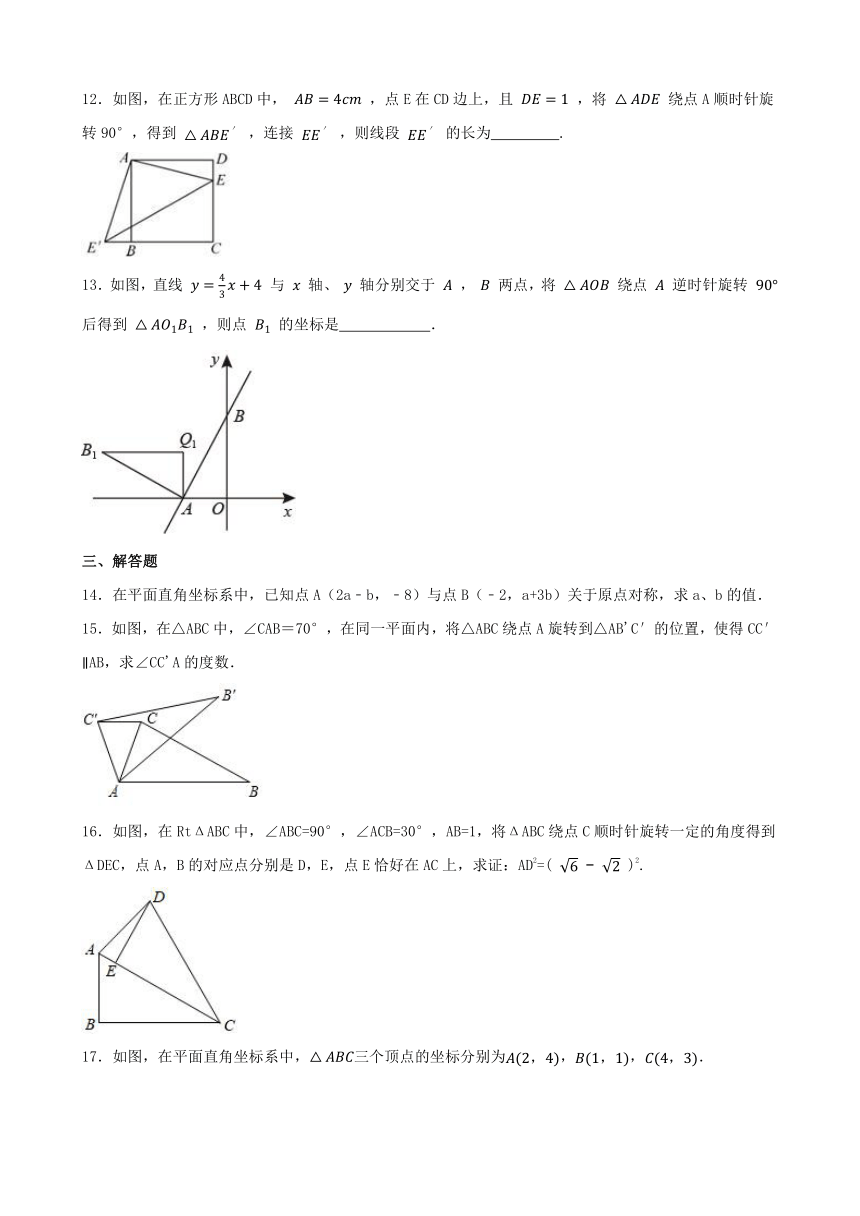
1.将如图所示的图形按逆时针方向旋转90°后得到图形是( )
A. B. C. D.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.如图,在正方形网格中,△ABC绕某点旋转一定的角度得到,则旋转中心是点( )
A.O B.P C.Q D.M
4.若与关于原点对称,则点落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,在正方形网格中,线段绕点旋转一定的角度后与线段重合、均为格点,的对应点是点,若点的坐标为,点的坐标为,则旋转中心点的坐标为( )
A. B.
C. D.或
6.在平面直角坐标系中,点A(5,m)与点B(-5,-3)关于原点对称,则m的值为( )
A.3 B.-3 C.5 D.-5
7.如图,在等腰中,,将绕点逆时针旋转得到,当点的对应点落在上时,连接,则的度数是( )
A.30° B.45° C.55° D.75°
8.如图,正方形 的两边 分别在x轴、y轴上,点 在边 上,以C为中心,把 旋转 ,则旋转后点D的对应点 的坐标是( ).
A. B.
C. 或 D. 或
二、填空题
9.若点M(a+1,2b-3)与点N(2a+1,-b-1)关于原点中心对称,则a+b= .
10.如图,将 绕直角顶点A顺时针旋转一定角度得到 ,点B的对应点D恰好落在 边上.若 ,则 的长为 .
11.如图,△DEC与△ABC关于点C成中心对称,AB=3,AC=1,∠D=90°,则AE的长是 .
12.如图,在正方形ABCD中, ,点E在CD边上,且 ,将 绕点A顺时针旋转90°,得到 ,连接 ,则线段 的长为 .
13.如图,直线 与 轴、 轴分别交于 , 两点,将 绕点 逆时针旋转 后得到 ,则点 的坐标是 .
三、解答题
14.在平面直角坐标系中,已知点A(2a﹣b,﹣8)与点B(﹣2,a+3b)关于原点对称,求a、b的值.
15.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C′的位置,使得CC′AB,求∠CC'A的度数.
16.如图,在RtΔABC中,∠ABC=90°,∠ACB=30°,AB=1,将ΔABC绕点C顺时针旋转一定的角度得到ΔDEC,点A,B的对应点分别是D,E,点E恰好在AC上,求证:AD2=( )2.
17.如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
⑴请画出关于原点对称的;
⑵请画出绕点B逆时针旋转后的,求点A到所经过的路径长.
18.如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,将△ABC绕点C逆时针旋转60°得到△CDE,点A、B的对应点分别是D、E,点F是边BC中点,连结AD、EF.
(1)求证:△ACD是等边三角形;
(2)判断AD与EF有怎样的数量关系,并说明理由.
参考答案
1.A
2.B
3.B
4.C
5.A
6.A
7.B
8.D
9.
10.1
11.
12.
13.
14.解:根据题意,得,解得.
15.解:∵,
∴∠ACC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠CC'A =70°,
16.解:在RtΔABC中,∠ABC=90°,∠ACB=30°,AB=1,
∴AC=2AB=2,BC= AB= ,
根据旋转的性质得:DE=AB=1,CE=BC= ,∠DEC=∠ABC=90°,
∴AE=AC-CE=2- ,∠AED=90°,
在RtΔADE中, ,
∴ .
17.解:⑴如图所示即为所求;
⑵如图所示即为所求,
,
点A到经过的路径长.
18.(1)证明:∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴AC=CD,∠ACD=60°,
∴△ACD是等边三角形;
(2)解:AD=EF,理由如下:
∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴∠BCE=60°,BC=CE,
∵△ACD是等边三角形,
∴AD=AC,
∵点F是边BC中点,
∴BC=2CF,
∵∠BAC=90°,∠ACB=30°,
∴BC=2AB,∠ABC=60°=∠BCE,
∴AB=CF,
在△ABC和△DEC中,
,
∴△ABC≌△FCE(SAS),
∴EF=AC,
∴AD=EF.
一、选择题
1.将如图所示的图形按逆时针方向旋转90°后得到图形是( )
A. B. C. D.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.如图,在正方形网格中,△ABC绕某点旋转一定的角度得到,则旋转中心是点( )
A.O B.P C.Q D.M
4.若与关于原点对称,则点落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,在正方形网格中,线段绕点旋转一定的角度后与线段重合、均为格点,的对应点是点,若点的坐标为,点的坐标为,则旋转中心点的坐标为( )
A. B.
C. D.或
6.在平面直角坐标系中,点A(5,m)与点B(-5,-3)关于原点对称,则m的值为( )
A.3 B.-3 C.5 D.-5
7.如图,在等腰中,,将绕点逆时针旋转得到,当点的对应点落在上时,连接,则的度数是( )
A.30° B.45° C.55° D.75°
8.如图,正方形 的两边 分别在x轴、y轴上,点 在边 上,以C为中心,把 旋转 ,则旋转后点D的对应点 的坐标是( ).
A. B.
C. 或 D. 或
二、填空题
9.若点M(a+1,2b-3)与点N(2a+1,-b-1)关于原点中心对称,则a+b= .
10.如图,将 绕直角顶点A顺时针旋转一定角度得到 ,点B的对应点D恰好落在 边上.若 ,则 的长为 .
11.如图,△DEC与△ABC关于点C成中心对称,AB=3,AC=1,∠D=90°,则AE的长是 .
12.如图,在正方形ABCD中, ,点E在CD边上,且 ,将 绕点A顺时针旋转90°,得到 ,连接 ,则线段 的长为 .
13.如图,直线 与 轴、 轴分别交于 , 两点,将 绕点 逆时针旋转 后得到 ,则点 的坐标是 .
三、解答题
14.在平面直角坐标系中,已知点A(2a﹣b,﹣8)与点B(﹣2,a+3b)关于原点对称,求a、b的值.
15.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C′的位置,使得CC′AB,求∠CC'A的度数.
16.如图,在RtΔABC中,∠ABC=90°,∠ACB=30°,AB=1,将ΔABC绕点C顺时针旋转一定的角度得到ΔDEC,点A,B的对应点分别是D,E,点E恰好在AC上,求证:AD2=( )2.
17.如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
⑴请画出关于原点对称的;
⑵请画出绕点B逆时针旋转后的,求点A到所经过的路径长.
18.如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,将△ABC绕点C逆时针旋转60°得到△CDE,点A、B的对应点分别是D、E,点F是边BC中点,连结AD、EF.
(1)求证:△ACD是等边三角形;
(2)判断AD与EF有怎样的数量关系,并说明理由.
参考答案
1.A
2.B
3.B
4.C
5.A
6.A
7.B
8.D
9.
10.1
11.
12.
13.
14.解:根据题意,得,解得.
15.解:∵,
∴∠ACC′=∠CAB=70°,
∵△ABC绕点A旋转到△AB′C′的位置,
∴AC=AC′,∠BAB′=∠CAC′,
在△ACC′中,∵AC=AC′
∴∠ACC′=∠CC'A =70°,
16.解:在RtΔABC中,∠ABC=90°,∠ACB=30°,AB=1,
∴AC=2AB=2,BC= AB= ,
根据旋转的性质得:DE=AB=1,CE=BC= ,∠DEC=∠ABC=90°,
∴AE=AC-CE=2- ,∠AED=90°,
在RtΔADE中, ,
∴ .
17.解:⑴如图所示即为所求;
⑵如图所示即为所求,
,
点A到经过的路径长.
18.(1)证明:∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴AC=CD,∠ACD=60°,
∴△ACD是等边三角形;
(2)解:AD=EF,理由如下:
∵将△ABC绕点C逆时针旋转60°得到△CDE,
∴∠BCE=60°,BC=CE,
∵△ACD是等边三角形,
∴AD=AC,
∵点F是边BC中点,
∴BC=2CF,
∵∠BAC=90°,∠ACB=30°,
∴BC=2AB,∠ABC=60°=∠BCE,
∴AB=CF,
在△ABC和△DEC中,
,
∴△ABC≌△FCE(SAS),
∴EF=AC,
∴AD=EF.
同课章节目录
