2023—2024学年人教版数学九年级上册 第22章 二次函数 单元综合训练 (无答案)
文档属性
| 名称 | 2023—2024学年人教版数学九年级上册 第22章 二次函数 单元综合训练 (无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 548.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 20:30:57 | ||
图片预览


文档简介
第22章 二次函数 单元综合训练
一、单选题
1.下列各式中,是关于的二次函数的是( )
A. B. C. D.
2.抛物线可由如何平移得到( )
A.先向右平移2个单位,再向下平移5个单位
B.先向右平移2个单位,再向上平移5个单位
C.先向左平移2个单位,再向下平移5个单位
D.先向左平移2个单位,再向上平移5个单位
3.若点,,是抛物线上的三点,则,,的大小关系为( )
A. B.
C. D.
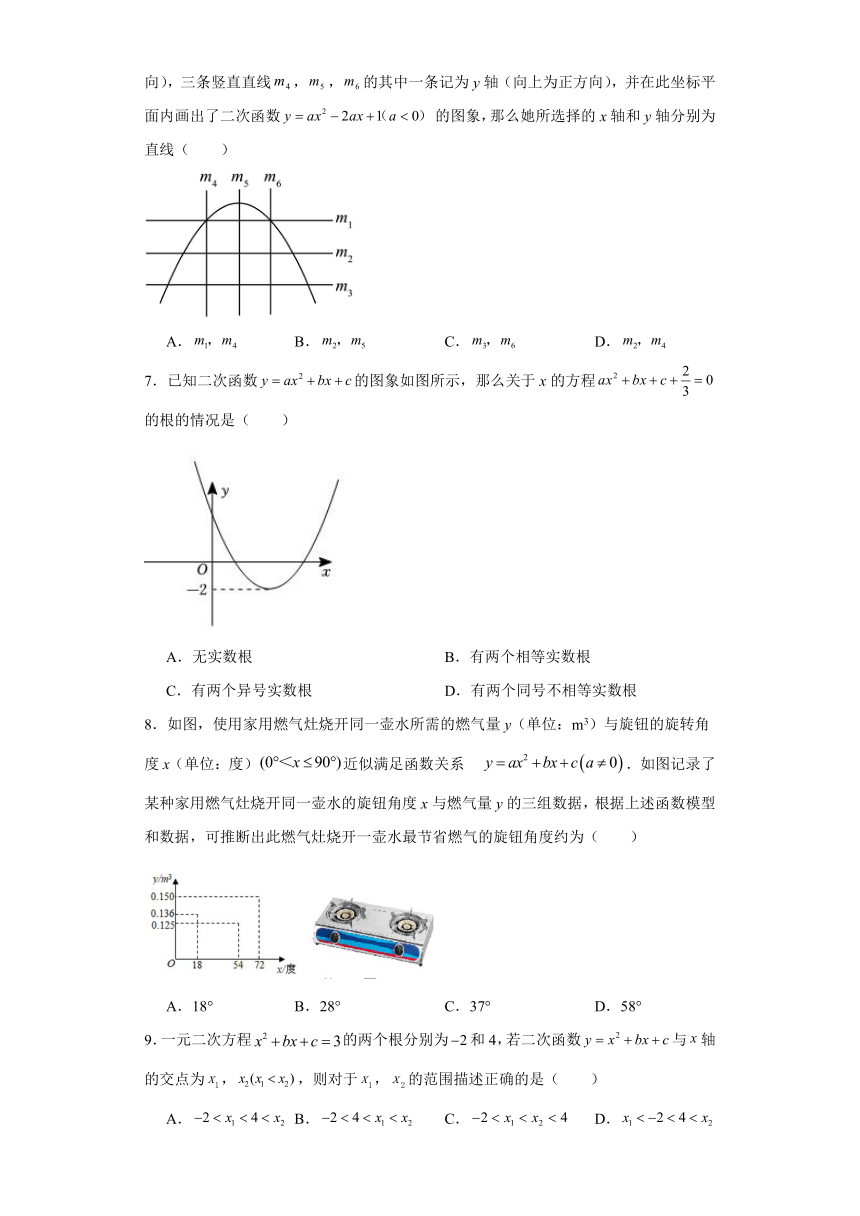
4.如图,下列选项中,能描述函数与的图象可能是( )
A. B.
C. D.
5.如表是二次函数的几组对应值:
x
根据表中数据判断,方程的一个解x的范围是( )
A. B.
C. D.
6.某同学将如图所示的三条水平直线,,的其中一条记为x轴(向右为正方向),三条竖直直线,,的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了二次函数 的图象,那么她所选择的x轴和y轴分别为直线( )
A. B. C. D.
7.已知二次函数的图象如图所示,那么关于x的方程的根的情况是( )
A.无实数根 B.有两个相等实数根
C.有两个异号实数根 D.有两个同号不相等实数根
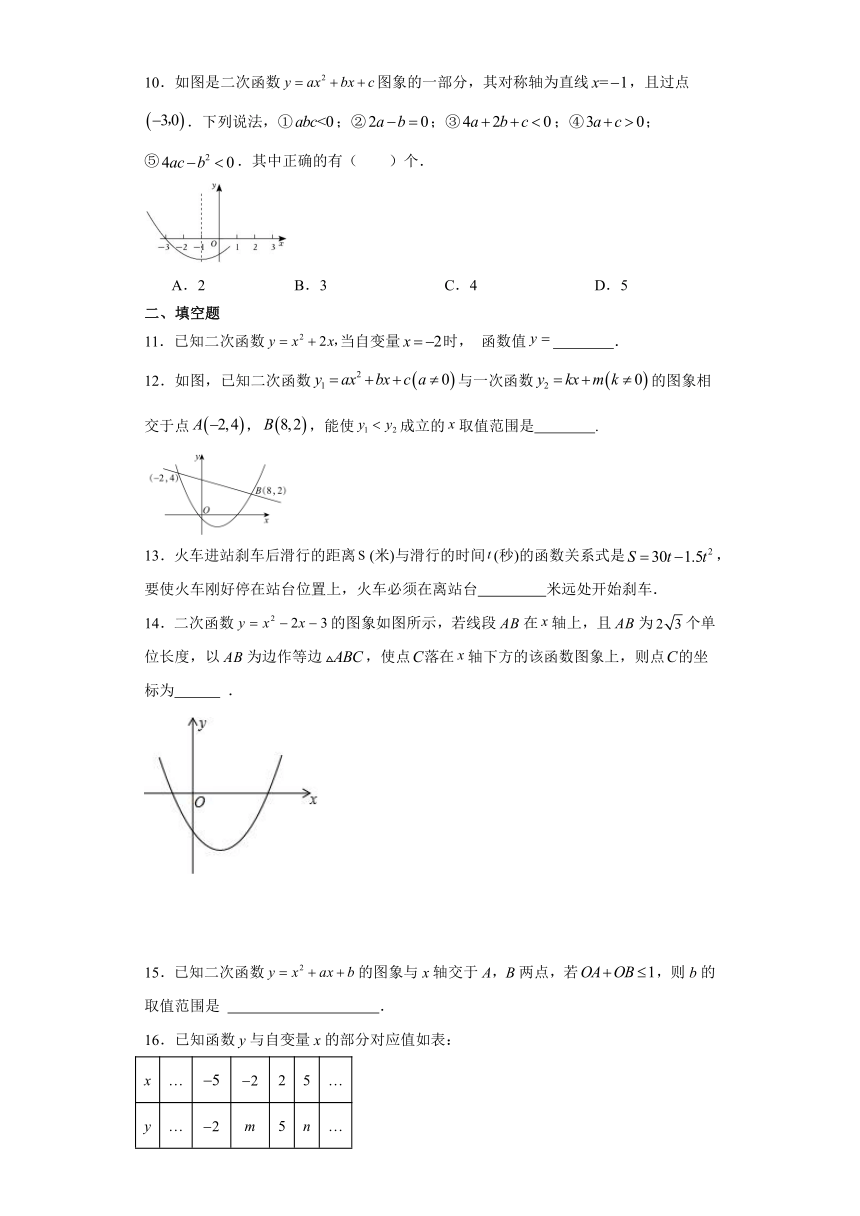
8.如图,使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)近似满足函数关系 .如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.18° B.28° C.37° D.58°
9.一元二次方程的两个根分别为和4,若二次函数与轴的交点为,,则对于,的范围描述正确的是( )
A. B. C. D.
10.如图是二次函数图象的一部分,其对称轴为直线,且过点.下列说法,①;②;③;④;⑤.其中正确的有( )个.
A.2 B.3 C.4 D.5
二、填空题
11.已知二次函数当自变量时, 函数值 .
12.如图,已知二次函数与一次函数的图象相交于点,,能使成立的取值范围是 .
13.火车进站刹车后滑行的距离(米)与滑行的时间(秒)的函数关系式是,要使火车刚好停在站台位置上,火车必须在离站台 米远处开始刹车.
14.二次函数的图象如图所示,若线段在轴上,且为个单位长度,以为边作等边,使点落在轴下方的该函数图象上,则点的坐标为 .
15.已知二次函数的图象与x轴交于A,B两点,若,则b的取值范围是 .
16.已知函数y与自变量x的部分对应值如表:
x … 2 5 …
y … m 5 n …
下列命题:①若y是x的反比例函数,则;②若y是x的一次函数,则;③若y是x的二次函数,且图象开口向下,则.其中正确的是 .(填写正确的序号)
三、解答题
17.已知抛物线交轴于,两点,交轴于点,求的面积.
18.如图,已知抛物线经过点和点两点.
(1)求抛物线的解析式和顶点坐标;
(2)通过计算判断点是否为抛物线上一点.
19.图,抛物线经过点,,三点,连接、、.
(1)求抛物线的函数表达式;
(2)是否存在点,使得以点为位似中心,将放大为原来的倍,得到点、、的对应点分别为点、、,使得点、恰好在抛物线上且点在抛物线的对称轴上?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.
20.苹果园有苹果树60棵,现准备多种一些苹果树提高苹果产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵苹果树时,果园内的每棵苹果树平均产量为.在确保每棵果树平均产量不低于40kg的前提下,设增种果树(且为整数)棵,该果园每棵果树平均产量为,它们之间的函数关系为一次函数,且满足如图所示的图象.
(1)图中点
所表示的实际意义是________,每增种1棵果树时,每棵果树平均产量减少________
;
(2)当增种果树多少棵时,果园的总产量
最大?最大产量是多少?
21.定义:如果两个二次函数的图像的开口大小相同,方向相反且顶点的横坐标、纵坐标都互为相反数,则称其中一个二次函数为另一个二次函数的美丽函数.如与互为美丽函数.
(1)求的美丽函数的表达式;
(2)若的图像的顶点为P,且经过它的美丽函数的图像的顶点Q.
①求证:这两个函数的图像的交点为P,Q;
②点M是在P,Q之间的图像的动点,轴交的图像于点N,求MN长度的最大值.
22.如图,二次函数的图象交x轴于点A,B,交y轴于点C,且,抛物线对称轴为直线.
(1)求这个二次函数的表达式;
(2)点在线段上运动(点P与A,O不重合),轴,交直线于点M,交抛物线于点N.
①求线段的最大值;
②当点M为的三等分点时,直接写出M的坐标.
23.如图(示意图),某跳水运动员进行10m跳台跳水训练,水面边缘点E的坐标为运动员(将运动员看成一点)在空中运动的路线是经过原点O的抛物线.在跳某个规定动作时,运动员在空中最高处点A的坐标为正常情况下,运动员在距水面高度5m以前,必须完成规定的翻腾、打开动作,并调整好入水姿势,否则就会失误.运动员入水后,运动路线为另一条抛物线.
(1)求运动员在空中运动时对应抛物线的函数解析式并求出入水处点B的坐标.
(2)若运动员在空中调整好入水姿势时,恰好距点E的水平距离为5m,该运动员此次跳水是否失误了 通过计算说明.
(3)在该运动员入水点的正前方有M,N两点,且,,该运动员入水后运动路线对应的抛物线的函数解析式为. 且顶点C距水面5m,若该运动员出水点D在之间(包括M,N两点),请直接写出a的取值范围.
24.如图1,抛物线:与x轴的正半轴交点B,与y轴交于点C,,其对称轴为直线.
(1)直接写出抛物线的解析式;
(2)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(3)如图2,作抛物线关于原点O中心对称的抛物线,若抛物线与直线交于E,F两点,与直线交于M,N两点,且,点P,Q分别是、的中点,求证:直线必定经过一个定点,并求出该定点坐标.
一、单选题
1.下列各式中,是关于的二次函数的是( )
A. B. C. D.
2.抛物线可由如何平移得到( )
A.先向右平移2个单位,再向下平移5个单位
B.先向右平移2个单位,再向上平移5个单位
C.先向左平移2个单位,再向下平移5个单位
D.先向左平移2个单位,再向上平移5个单位
3.若点,,是抛物线上的三点,则,,的大小关系为( )
A. B.
C. D.
4.如图,下列选项中,能描述函数与的图象可能是( )
A. B.
C. D.
5.如表是二次函数的几组对应值:
x
根据表中数据判断,方程的一个解x的范围是( )
A. B.
C. D.
6.某同学将如图所示的三条水平直线,,的其中一条记为x轴(向右为正方向),三条竖直直线,,的其中一条记为y轴(向上为正方向),并在此坐标平面内画出了二次函数 的图象,那么她所选择的x轴和y轴分别为直线( )
A. B. C. D.
7.已知二次函数的图象如图所示,那么关于x的方程的根的情况是( )
A.无实数根 B.有两个相等实数根
C.有两个异号实数根 D.有两个同号不相等实数根
8.如图,使用家用燃气灶烧开同一壶水所需的燃气量y(单位:m3)与旋钮的旋转角度x(单位:度)近似满足函数关系 .如图记录了某种家用燃气灶烧开同一壶水的旋钮角度x与燃气量y的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A.18° B.28° C.37° D.58°
9.一元二次方程的两个根分别为和4,若二次函数与轴的交点为,,则对于,的范围描述正确的是( )
A. B. C. D.
10.如图是二次函数图象的一部分,其对称轴为直线,且过点.下列说法,①;②;③;④;⑤.其中正确的有( )个.
A.2 B.3 C.4 D.5
二、填空题
11.已知二次函数当自变量时, 函数值 .
12.如图,已知二次函数与一次函数的图象相交于点,,能使成立的取值范围是 .
13.火车进站刹车后滑行的距离(米)与滑行的时间(秒)的函数关系式是,要使火车刚好停在站台位置上,火车必须在离站台 米远处开始刹车.
14.二次函数的图象如图所示,若线段在轴上,且为个单位长度,以为边作等边,使点落在轴下方的该函数图象上,则点的坐标为 .
15.已知二次函数的图象与x轴交于A,B两点,若,则b的取值范围是 .
16.已知函数y与自变量x的部分对应值如表:
x … 2 5 …
y … m 5 n …
下列命题:①若y是x的反比例函数,则;②若y是x的一次函数,则;③若y是x的二次函数,且图象开口向下,则.其中正确的是 .(填写正确的序号)
三、解答题
17.已知抛物线交轴于,两点,交轴于点,求的面积.
18.如图,已知抛物线经过点和点两点.
(1)求抛物线的解析式和顶点坐标;
(2)通过计算判断点是否为抛物线上一点.
19.图,抛物线经过点,,三点,连接、、.
(1)求抛物线的函数表达式;
(2)是否存在点,使得以点为位似中心,将放大为原来的倍,得到点、、的对应点分别为点、、,使得点、恰好在抛物线上且点在抛物线的对称轴上?若存在,求出所有符合条件的点的坐标;若不存在,请说明理由.
20.苹果园有苹果树60棵,现准备多种一些苹果树提高苹果产量.如果多种树,那么树之间的距离和每棵果树所受光照就会减少,每棵果树的平均产量随之降低.根据经验,增种10棵苹果树时,果园内的每棵苹果树平均产量为.在确保每棵果树平均产量不低于40kg的前提下,设增种果树(且为整数)棵,该果园每棵果树平均产量为,它们之间的函数关系为一次函数,且满足如图所示的图象.
(1)图中点
所表示的实际意义是________,每增种1棵果树时,每棵果树平均产量减少________
;
(2)当增种果树多少棵时,果园的总产量
最大?最大产量是多少?
21.定义:如果两个二次函数的图像的开口大小相同,方向相反且顶点的横坐标、纵坐标都互为相反数,则称其中一个二次函数为另一个二次函数的美丽函数.如与互为美丽函数.
(1)求的美丽函数的表达式;
(2)若的图像的顶点为P,且经过它的美丽函数的图像的顶点Q.
①求证:这两个函数的图像的交点为P,Q;
②点M是在P,Q之间的图像的动点,轴交的图像于点N,求MN长度的最大值.
22.如图,二次函数的图象交x轴于点A,B,交y轴于点C,且,抛物线对称轴为直线.
(1)求这个二次函数的表达式;
(2)点在线段上运动(点P与A,O不重合),轴,交直线于点M,交抛物线于点N.
①求线段的最大值;
②当点M为的三等分点时,直接写出M的坐标.
23.如图(示意图),某跳水运动员进行10m跳台跳水训练,水面边缘点E的坐标为运动员(将运动员看成一点)在空中运动的路线是经过原点O的抛物线.在跳某个规定动作时,运动员在空中最高处点A的坐标为正常情况下,运动员在距水面高度5m以前,必须完成规定的翻腾、打开动作,并调整好入水姿势,否则就会失误.运动员入水后,运动路线为另一条抛物线.
(1)求运动员在空中运动时对应抛物线的函数解析式并求出入水处点B的坐标.
(2)若运动员在空中调整好入水姿势时,恰好距点E的水平距离为5m,该运动员此次跳水是否失误了 通过计算说明.
(3)在该运动员入水点的正前方有M,N两点,且,,该运动员入水后运动路线对应的抛物线的函数解析式为. 且顶点C距水面5m,若该运动员出水点D在之间(包括M,N两点),请直接写出a的取值范围.
24.如图1,抛物线:与x轴的正半轴交点B,与y轴交于点C,,其对称轴为直线.
(1)直接写出抛物线的解析式;
(2)若点D是抛物线对称轴上的动点,点G是抛物线上的动点,是否存在以点B、C、D、G为顶点的四边形是平行四边形.若存在,求出点G的坐标;若不存在,试说明理由.
(3)如图2,作抛物线关于原点O中心对称的抛物线,若抛物线与直线交于E,F两点,与直线交于M,N两点,且,点P,Q分别是、的中点,求证:直线必定经过一个定点,并求出该定点坐标.
同课章节目录
