2023-2024学年人教版九年级数学上册 第23章 旋转 单元综合训练(无答案)
文档属性
| 名称 | 2023-2024学年人教版九年级数学上册 第23章 旋转 单元综合训练(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 606.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 20:31:40 | ||
图片预览

文档简介
第23章 旋转 单元综合训练
一、单选题
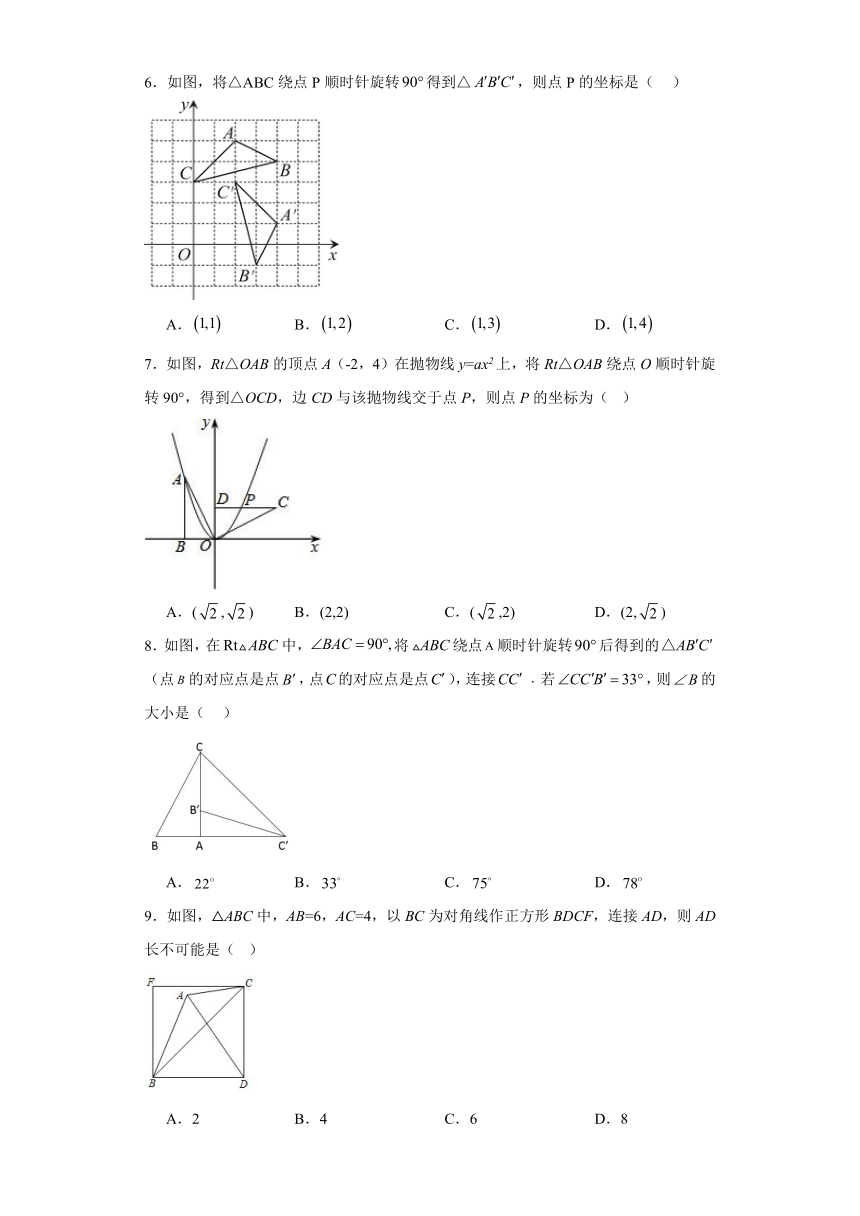
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.将数字“6”旋转,得到数字“9”;将数字“9”旋转,得到的数字是“6”,现将数字“69”旋转,得到的数字是( )
A.96 B.69 C.66 D.99
3.如图, 与 关于点 成中心对称,则下列结论不成立的是( )
A.点与点是对称点 B. C. D.
4.如图,将绕点A按逆时针方向旋转,得到,若点在线段的延长线上,则的度数为( ).
A. B. C. D.
5.如图,已知中,,,,若把绕点A逆时针旋转一个角度,使它与原的重叠部分为等腰三角形.则为( )
A.或 B.或 C.或 D.或
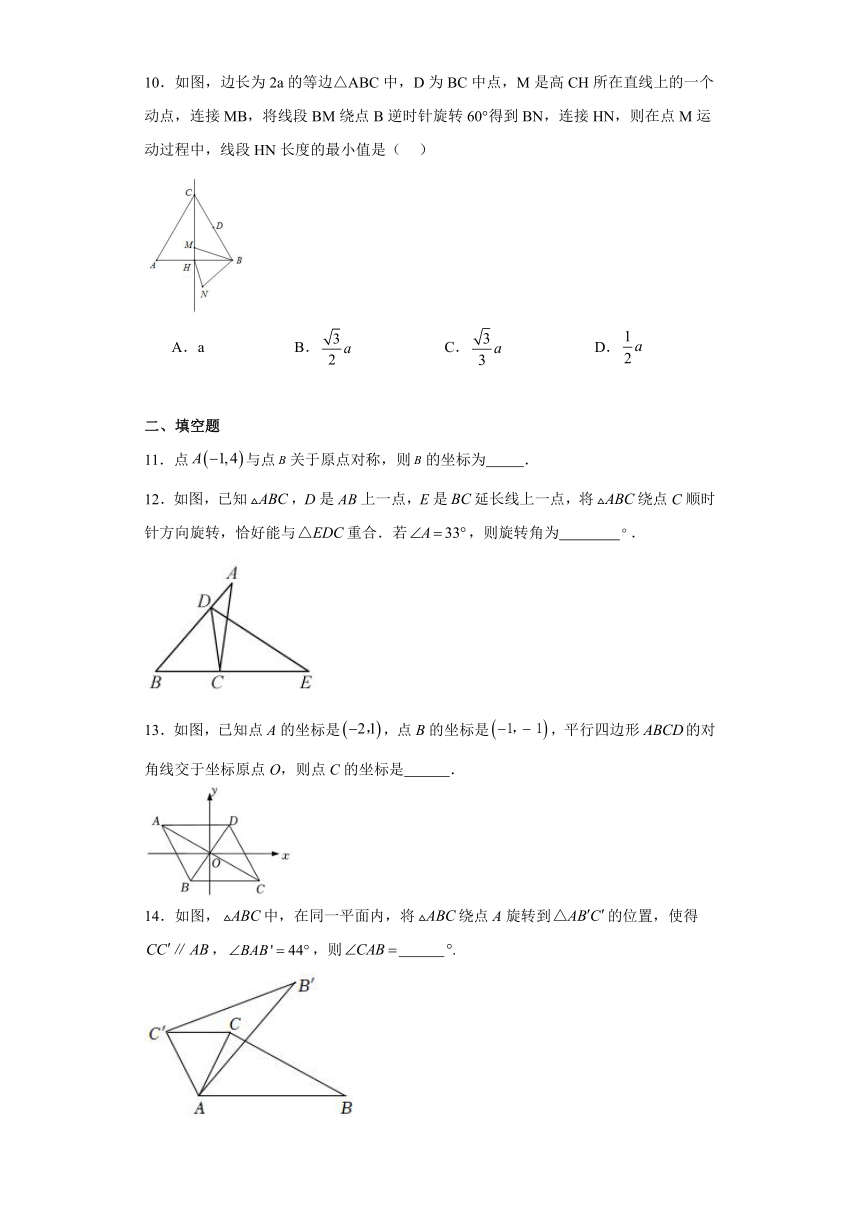
6.如图,将△ABC绕点P顺时针旋转得到△,则点P的坐标是( )
A. B. C. D.
7.如图,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
A.(,) B.(2,2) C.(,2) D.(2,)
8.如图,在中,将绕点顺时针旋转后得到的(点的对应点是点,点的对应点是点),连接﹒若,则的大小是( )
A. B. C. D.
9.如图,△ABC中,AB=6,AC=4,以BC为对角线作正方形BDCF,连接AD,则AD长不可能是( )
A.2 B.4 C.6 D.8
10.如图,边长为2a的等边△ABC中,D为BC中点,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN,则在点M运动过程中,线段HN长度的最小值是( )
A.a B. C. D.
二、填空题
11.点与点关于原点对称,则的坐标为 .
12.如图,已知,D是上一点,E是延长线上一点,将绕点C顺时针方向旋转,恰好能与重合.若,则旋转角为 .
13.如图,已知点A的坐标是,点B的坐标是,平行四边形的对角线交于坐标原点O,则点C的坐标是 .
14.如图,中,在同一平面内,将绕点A旋转到的位置,使得,,则
15.如图,点A是抛物线对称轴上的一动点,连接,以A为旋转中心将AO逆时针旋转90°得到,当恰好落在抛物线上时,点A的坐标为 .
16.定义:在平面内, 一个点到图形的距离是这个点到这个图上所有点的最短距离. 如图, 在平面内有一个正方形, 边长为3 , 中心为, 在正方形外有点,, 当正方形绕着点 旋转时, 则点到正方形的最短距离的取值范围为 .
三、解答题
17.如图所示,已知两个三角形成中心对称关系.请画出对称中心.
18.在3×3的正方形格点图中,△ABC和△DEF是关于某条直线成轴对称的两个格点三角形,现给出了△ABC,在下面的图中画出5个符合条件的△DEF,并画出对称轴.
19.如图,平面直角坐标系中, 的顶点坐标分别为,,.
(1)请在图中作出与关于原点对称的图形;
(2)点的坐标是________;点的坐标是________.
20.如图,中,点E在边上,,将线段绕点A旋转到的位置,使得.连接,与交于点G.
(1)求证:;
(2)若,,求的度数.
21.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
22.在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD分割成四个部分,使含有一组对顶角的两个图形全等;
( 1 )根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有 组;
( 2 )请在图中的三个平行四边形中画出满足小强分割方法的直线;
( 3 )由上述实验操作过程,你发现所画的两条直线有什么规律?
23.如图,已知正方形ABCD,点M是线段CB延长线上一点,联结AM,AB=a,BM=b.
(1)将线段AM沿着射线AD方向平移,使得点A与点D重合. 用代数式表示线段AM扫过平面部分的面积 .(直接写出答案)
(2)将三角形ABM绕着点A旋转,使得AB与AD重合,点M落在点N,联结MN. 用代数式表示三角形CMN的面积 .(直接写出答案)
(3)将三角形ABM顺时针旋转,使旋转后的三角形有一边与正方形的一边完全重合(第(2)小题的情况除外).请在下图中画出符合条件的3种情况,并写出相应的旋转中心和旋转角.
24.明遇到这样一个问题:如图①,在四边形ABCD中,∠B=40°,∠C=50°,AB=CD,AD=2,BC=4,求四边形ABCD的面积.
(1)经过思考小明想到如下方法:
以BC为边作正方形BCMN,将四边形ABCD绕着正方形BCMN的中心按顺时针方向旋转90°,180°,270°,而分别得到四边形FNBA,EMNF,DCME,则四边形ADEF是________.(填一种特殊的平行四边形)
∴S四边形ABCD=________.
(2)解决问题:如图③,在四边形ABCD中,∠BAD=140°,∠CDA=160°,AB=CD,AD=6,BC=12,则四边形ABCD的面积为多少?
一、单选题
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.将数字“6”旋转,得到数字“9”;将数字“9”旋转,得到的数字是“6”,现将数字“69”旋转,得到的数字是( )
A.96 B.69 C.66 D.99
3.如图, 与 关于点 成中心对称,则下列结论不成立的是( )
A.点与点是对称点 B. C. D.
4.如图,将绕点A按逆时针方向旋转,得到,若点在线段的延长线上,则的度数为( ).
A. B. C. D.
5.如图,已知中,,,,若把绕点A逆时针旋转一个角度,使它与原的重叠部分为等腰三角形.则为( )
A.或 B.或 C.或 D.或
6.如图,将△ABC绕点P顺时针旋转得到△,则点P的坐标是( )
A. B. C. D.
7.如图,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
A.(,) B.(2,2) C.(,2) D.(2,)
8.如图,在中,将绕点顺时针旋转后得到的(点的对应点是点,点的对应点是点),连接﹒若,则的大小是( )
A. B. C. D.
9.如图,△ABC中,AB=6,AC=4,以BC为对角线作正方形BDCF,连接AD,则AD长不可能是( )
A.2 B.4 C.6 D.8
10.如图,边长为2a的等边△ABC中,D为BC中点,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN,则在点M运动过程中,线段HN长度的最小值是( )
A.a B. C. D.
二、填空题
11.点与点关于原点对称,则的坐标为 .
12.如图,已知,D是上一点,E是延长线上一点,将绕点C顺时针方向旋转,恰好能与重合.若,则旋转角为 .
13.如图,已知点A的坐标是,点B的坐标是,平行四边形的对角线交于坐标原点O,则点C的坐标是 .
14.如图,中,在同一平面内,将绕点A旋转到的位置,使得,,则
15.如图,点A是抛物线对称轴上的一动点,连接,以A为旋转中心将AO逆时针旋转90°得到,当恰好落在抛物线上时,点A的坐标为 .
16.定义:在平面内, 一个点到图形的距离是这个点到这个图上所有点的最短距离. 如图, 在平面内有一个正方形, 边长为3 , 中心为, 在正方形外有点,, 当正方形绕着点 旋转时, 则点到正方形的最短距离的取值范围为 .
三、解答题
17.如图所示,已知两个三角形成中心对称关系.请画出对称中心.
18.在3×3的正方形格点图中,△ABC和△DEF是关于某条直线成轴对称的两个格点三角形,现给出了△ABC,在下面的图中画出5个符合条件的△DEF,并画出对称轴.
19.如图,平面直角坐标系中, 的顶点坐标分别为,,.
(1)请在图中作出与关于原点对称的图形;
(2)点的坐标是________;点的坐标是________.
20.如图,中,点E在边上,,将线段绕点A旋转到的位置,使得.连接,与交于点G.
(1)求证:;
(2)若,,求的度数.
21.如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)当点D在AC上时,如图①,线段BD,CE有怎样的数量关系和位置关系?请证明你的猜想;
(2)将图①中的△ADE绕点A顺时针旋转α(0°<α<90°),如图②,线段BD,CE有怎样的数量关系和位置关系?请说明理由.
22.在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD分割成四个部分,使含有一组对顶角的两个图形全等;
( 1 )根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有 组;
( 2 )请在图中的三个平行四边形中画出满足小强分割方法的直线;
( 3 )由上述实验操作过程,你发现所画的两条直线有什么规律?
23.如图,已知正方形ABCD,点M是线段CB延长线上一点,联结AM,AB=a,BM=b.
(1)将线段AM沿着射线AD方向平移,使得点A与点D重合. 用代数式表示线段AM扫过平面部分的面积 .(直接写出答案)
(2)将三角形ABM绕着点A旋转,使得AB与AD重合,点M落在点N,联结MN. 用代数式表示三角形CMN的面积 .(直接写出答案)
(3)将三角形ABM顺时针旋转,使旋转后的三角形有一边与正方形的一边完全重合(第(2)小题的情况除外).请在下图中画出符合条件的3种情况,并写出相应的旋转中心和旋转角.
24.明遇到这样一个问题:如图①,在四边形ABCD中,∠B=40°,∠C=50°,AB=CD,AD=2,BC=4,求四边形ABCD的面积.
(1)经过思考小明想到如下方法:
以BC为边作正方形BCMN,将四边形ABCD绕着正方形BCMN的中心按顺时针方向旋转90°,180°,270°,而分别得到四边形FNBA,EMNF,DCME,则四边形ADEF是________.(填一种特殊的平行四边形)
∴S四边形ABCD=________.
(2)解决问题:如图③,在四边形ABCD中,∠BAD=140°,∠CDA=160°,AB=CD,AD=6,BC=12,则四边形ABCD的面积为多少?
同课章节目录
