人教版数学九上旋转模型(奔驰、手拉手、最值路径) 讲义(无答案)
文档属性
| 名称 | 人教版数学九上旋转模型(奔驰、手拉手、最值路径) 讲义(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 162.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 08:03:20 | ||
图片预览


文档简介
旋转---奔驰模型 讲义
[模型讲解]
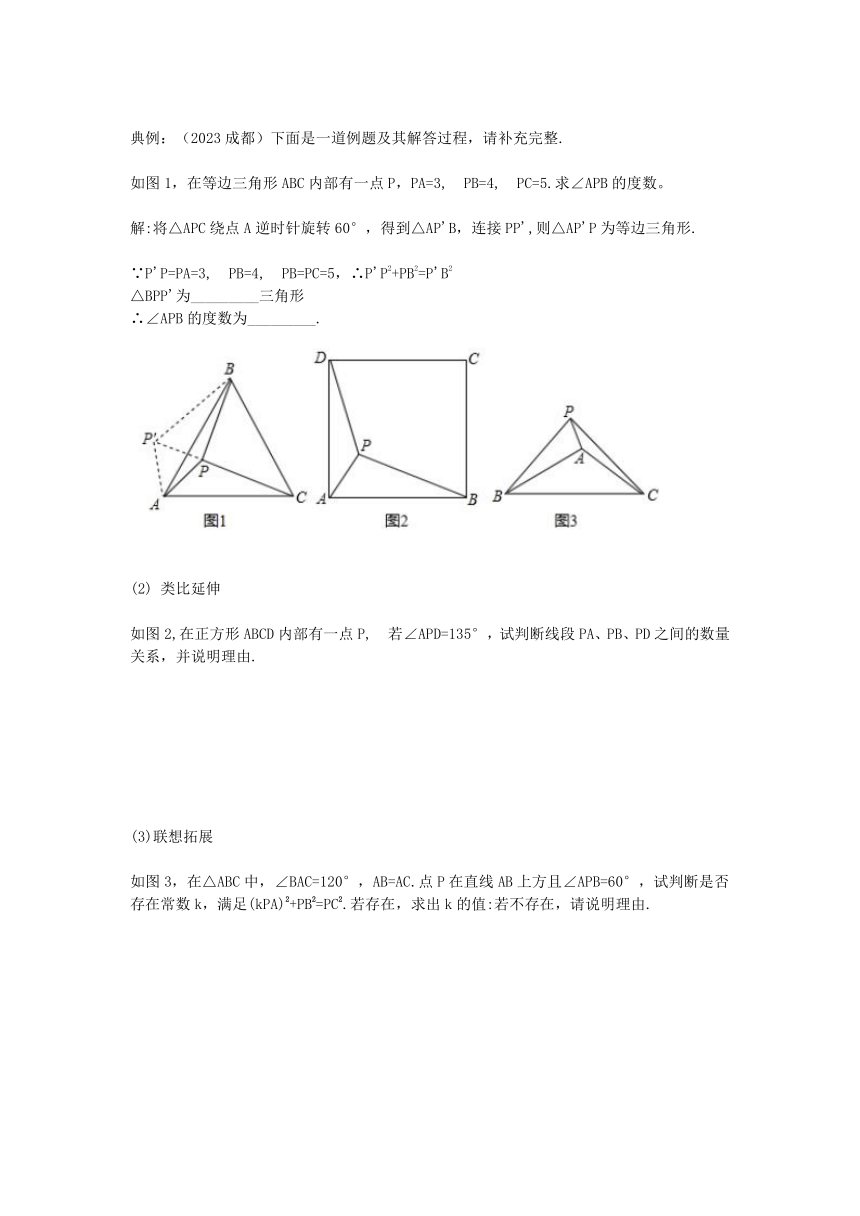
如图所示,在等边△ABC中,DA=3,DB=4,DC=5,则∠ADB=_______
思路:解决本题的关键是利用旋转让线段动起来,利用旋转构造手拉手模型证明全等,结合勾股定理,得到结论,请选择一种方法证明。
证明:
拓展:如上图所示,条件不变的情况下,请求出△ABC的面积
尝试练习:
1、如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,,若△APB绕点A逆时针旋转600后,得到△AP’C,则∠APC=_______
2、如图所示,在等边△ABC中,PA=8,PB=15,PC=17,则△ABC的面积=_______
典例:(2023成都)下面是一道例题及其解答过程,请补充完整.
如图1,在等边三角形ABC内部有一点P,PA=3, PB=4, PC=5.求∠APB的度数。
解:将△APC绕点A逆时针旋转60°,得到△AP'B,连接PP',则△AP'P为等边三角形.
∵P'P=PA=3, PB=4, PB=PC=5,∴P'P2+PB2=P'B2
△BPP'为_________三角形
∴∠APB的度数为_________.
类比延伸
如图2,在正方形ABCD内部有一点P, 若∠APD=135°,试判断线段PA、PB、PD之间的数量关系,并说明理由.
(3)联想拓展
如图3,在△ABC中,∠BAC=120°,AB=AC.点P在直线AB上方且∠APB=60°,试判断是否存在常数k,满足(kPA)2+PB2=PC2.若存在,求出k的值:若不存在,请说明理由.
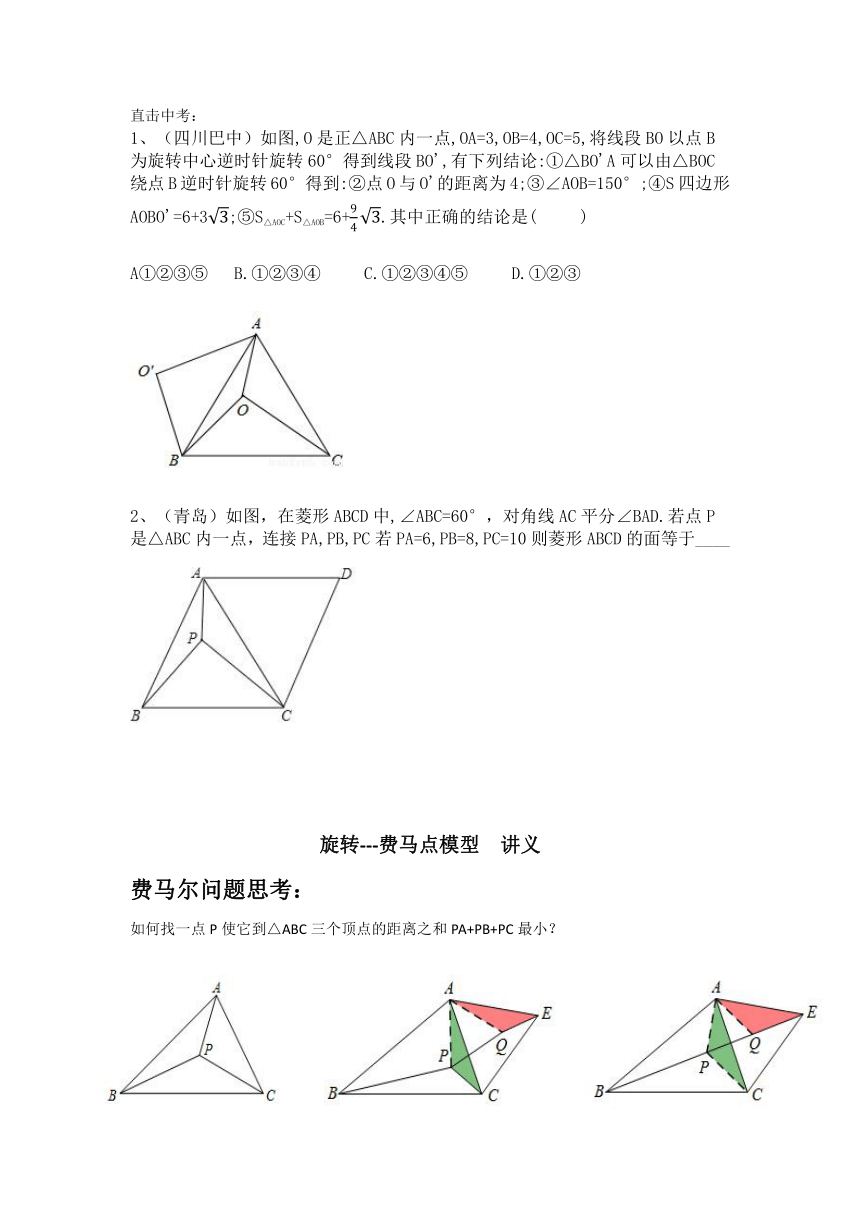
直击中考:
(四川巴中)如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',有下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到:②点O与O'的距离为4;③∠AOB=150°;④S四边形AOBO'=6+3;⑤S△AOC+S△AOB=6+.其中正确的结论是( )
A①②③⑤ B.①②③④ C.①②③④⑤ D.①②③
2、(青岛)如图,在菱形ABCD中,∠ABC=60°,对角线AC平分∠BAD.若点P是△ABC内一点,连接PA,PB,PC若PA=6,PB=8,PC=10则菱形ABCD的面等于____
旋转---费马点模型 讲义
费马尔问题思考:
如何找一点P使它到△ABC三个顶点的距离之和PA+PB+PC最小?
当B、P、Q、E四点共线时取得最小值
费马点的定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:
1. 如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;
2. 如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
费马点的性质:费马点有如下主要性质:
1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值快速求解:
费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.
秘诀:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值
典例:已知,在△ABC中,∠ACB=30°
(1)如图1,当AB=AC=2,求BC的值;
(2)如图2,当AB=AC,点P是△ABC内一点,且PA=2,PB=,PC=3,求∠APC的度数;
(3)如图3,当AC=4,AB=(CB>CA),点P是△ABC内一动点,则PA+PB+PC的最小值为 .
变式练习:
1、 如图,P为正方形ABCD对角线BD上一动点,若AB=2,则AP+BP+CP的最小值为( )
A.+ B.+ C.4 D.3
2、如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为______.
3、将△ABC放在每个小正方形的边长为1的网格中,点B、C落在格点上,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB= 度;
(2)如图,将△APC绕点C顺时针旋转60°,画出旋转后的图形(尺规作图,保留痕迹);
(3)AP+BP+CP的最小值为 .
4、如图l,在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB=6时,根据此图求PA+PB+PC的最小值.
旋转---最值、路径长 讲义
模型 (瓜豆原理)绕定点旋转
PA绕定点A逆时针旋转得到线段AA'.
基本结论:
点A'在与定直线a所夹的锐角为的定直线b上运动.
解决方法:手拉手构造旋转全等
题型一 运用垂线段最短求最值
【例1】如图,等边△ABC边长为6,点E是中线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF,在点E运动过程中,DF的最小值为 .
【例2】如图,点B(0,3),点A为x轴上一动点,将线段AB绕点A顺时针旋转90°得AC,连接OC,求OC长的最小值.
针对练习:1、如图,在△ABC中,∠C=90°,BC=6,AC=10,D为线段AC上一动点,将线段BD绕点D逆时针旋转90°.点B的对应点为点E,连接AE,求AE长的最小值.
2、如图,在平面直角坐标系中,直线y=x-1分别交x轴,y轴于点B,点A,点M为直线AB上一动点,连接OM,将线段OM绕点M逆时针旋转90°,点O的对应点为点N.当点M运动时,判断点N的运动路线是什么图形,并说明理由.
3、如图,矩形ABCD中,BC=2AB=8.点M,N分别为AD,BC的中点,连接MN,点P是BC边上的动点,将PM绕点P顺时针方向旋转90°得PE,当点P从点B运动到点C的过程中,点E运动的路径长为 .
题型二 运用两边之和大于第三边求最值
【例3】如图,在直角△ABC中,∠ACB=90°,BC=AC=5,BP=2,将PC绕点C逆时针旋转90°得线段CD,连接BD,当BP绕点B旋转时,线段BD的最小值为 .
针对练习1、如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,将PB绕点P逆时针旋转90°得PM,求AM长的最大值.
针对练习2、如图,边长为4的正方形ABCD外有点E ,∠AEB=90°,F为DE的中点,连接CF.求CF的最大值.
[模型讲解]
如图所示,在等边△ABC中,DA=3,DB=4,DC=5,则∠ADB=_______
思路:解决本题的关键是利用旋转让线段动起来,利用旋转构造手拉手模型证明全等,结合勾股定理,得到结论,请选择一种方法证明。
证明:
拓展:如上图所示,条件不变的情况下,请求出△ABC的面积
尝试练习:
1、如图,P是等边△ABC内一点,且PA=6,PC=8,PB=10,,若△APB绕点A逆时针旋转600后,得到△AP’C,则∠APC=_______
2、如图所示,在等边△ABC中,PA=8,PB=15,PC=17,则△ABC的面积=_______
典例:(2023成都)下面是一道例题及其解答过程,请补充完整.
如图1,在等边三角形ABC内部有一点P,PA=3, PB=4, PC=5.求∠APB的度数。
解:将△APC绕点A逆时针旋转60°,得到△AP'B,连接PP',则△AP'P为等边三角形.
∵P'P=PA=3, PB=4, PB=PC=5,∴P'P2+PB2=P'B2
△BPP'为_________三角形
∴∠APB的度数为_________.
类比延伸
如图2,在正方形ABCD内部有一点P, 若∠APD=135°,试判断线段PA、PB、PD之间的数量关系,并说明理由.
(3)联想拓展
如图3,在△ABC中,∠BAC=120°,AB=AC.点P在直线AB上方且∠APB=60°,试判断是否存在常数k,满足(kPA)2+PB2=PC2.若存在,求出k的值:若不存在,请说明理由.
直击中考:
(四川巴中)如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',有下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到:②点O与O'的距离为4;③∠AOB=150°;④S四边形AOBO'=6+3;⑤S△AOC+S△AOB=6+.其中正确的结论是( )
A①②③⑤ B.①②③④ C.①②③④⑤ D.①②③
2、(青岛)如图,在菱形ABCD中,∠ABC=60°,对角线AC平分∠BAD.若点P是△ABC内一点,连接PA,PB,PC若PA=6,PB=8,PC=10则菱形ABCD的面等于____
旋转---费马点模型 讲义
费马尔问题思考:
如何找一点P使它到△ABC三个顶点的距离之和PA+PB+PC最小?
当B、P、Q、E四点共线时取得最小值
费马点的定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:
1. 如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;
2. 如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
费马点的性质:费马点有如下主要性质:
1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值快速求解:
费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.
秘诀:以△ABC任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值
典例:已知,在△ABC中,∠ACB=30°
(1)如图1,当AB=AC=2,求BC的值;
(2)如图2,当AB=AC,点P是△ABC内一点,且PA=2,PB=,PC=3,求∠APC的度数;
(3)如图3,当AC=4,AB=(CB>CA),点P是△ABC内一动点,则PA+PB+PC的最小值为 .
变式练习:
1、 如图,P为正方形ABCD对角线BD上一动点,若AB=2,则AP+BP+CP的最小值为( )
A.+ B.+ C.4 D.3
2、如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为______.
3、将△ABC放在每个小正方形的边长为1的网格中,点B、C落在格点上,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB= 度;
(2)如图,将△APC绕点C顺时针旋转60°,画出旋转后的图形(尺规作图,保留痕迹);
(3)AP+BP+CP的最小值为 .
4、如图l,在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB=6时,根据此图求PA+PB+PC的最小值.
旋转---最值、路径长 讲义
模型 (瓜豆原理)绕定点旋转
PA绕定点A逆时针旋转得到线段AA'.
基本结论:
点A'在与定直线a所夹的锐角为的定直线b上运动.
解决方法:手拉手构造旋转全等
题型一 运用垂线段最短求最值
【例1】如图,等边△ABC边长为6,点E是中线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF,在点E运动过程中,DF的最小值为 .
【例2】如图,点B(0,3),点A为x轴上一动点,将线段AB绕点A顺时针旋转90°得AC,连接OC,求OC长的最小值.
针对练习:1、如图,在△ABC中,∠C=90°,BC=6,AC=10,D为线段AC上一动点,将线段BD绕点D逆时针旋转90°.点B的对应点为点E,连接AE,求AE长的最小值.
2、如图,在平面直角坐标系中,直线y=x-1分别交x轴,y轴于点B,点A,点M为直线AB上一动点,连接OM,将线段OM绕点M逆时针旋转90°,点O的对应点为点N.当点M运动时,判断点N的运动路线是什么图形,并说明理由.
3、如图,矩形ABCD中,BC=2AB=8.点M,N分别为AD,BC的中点,连接MN,点P是BC边上的动点,将PM绕点P顺时针方向旋转90°得PE,当点P从点B运动到点C的过程中,点E运动的路径长为 .
题型二 运用两边之和大于第三边求最值
【例3】如图,在直角△ABC中,∠ACB=90°,BC=AC=5,BP=2,将PC绕点C逆时针旋转90°得线段CD,连接BD,当BP绕点B旋转时,线段BD的最小值为 .
针对练习1、如图,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,将PB绕点P逆时针旋转90°得PM,求AM长的最大值.
针对练习2、如图,边长为4的正方形ABCD外有点E ,∠AEB=90°,F为DE的中点,连接CF.求CF的最大值.
同课章节目录
