6.2《多位数乘一位数(不进位)的笔算乘法》(教案)-三年级 上册数学人教版
文档属性
| 名称 | 6.2《多位数乘一位数(不进位)的笔算乘法》(教案)-三年级 上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 21:52:11 | ||
图片预览


文档简介
《多位数乘一位数(不进位)的笔算乘法》教学设计
备教材内容
本课时学习的是教材60页的内容及相关习题。本课时的学习建立在学生知道了乘法算式各部分的名称、掌握了表内乘法、整十、整百数乘一位数和两位数乘一位数(不进位)的口算方法等基础之上。本课时的内容是本单元教学的重点,同时也是继续学习多位数乘法的基础。教材创设了生活中的实际情境,从解决问题入手,体现了计算的实用价值。在计算中,体现算法多样化,呈现连加、口算和列乘法竖式计算等多种算法。呈现乘法竖式的几个环节,重点教学乘法竖式的笔算方法,让学生经历乘法竖式形成的过程,理解乘法竖式计算中每一步的算理,掌握算法。另外教材安排了做一做两道有层次性的对比练习,既为了正确书写竖式,同时也进一步巩固了笔算方法。
备教法学法
从素质教育着眼来看,要贯彻传授知识与培养能力相结合的原则,不仅要使学生学会知识,更要使学生会学、乐学、自主去学。
为了充分发挥学生的主体地位,使他们能够自主学习,切实提高课堂教学效率。采用谈话激趣、自主尝试、讨论归纳、强化练习等教学方法,循循诱导,让学生在尝试、迁移、类推、合作中自主学习,巩固和拓展所学知识。
教学目标
1、能够比较熟练地口算整十、整百、整千数乘一位数,两位数乘一位数(不进位)。
2、通过对比辨析,总结概括口算的计算方法,进一步理解算理,掌握算法。
3、能够运用所学知识,解决生活中的简单问题,提高解决问题的能力。
教学重难点
教学重点:
感受口算乘法的算法优化。
教学难点:
掌握口算乘法的方法。
备已学知识
1.整十、整百数乘一位数的口算方法:先把整十、整百数后面的0去掉,再相乘,计算出积后,在积的末尾添上之前去掉的0。
2.两位数乘一位数(不进位)的口算方法:把两位数分成整十数和一位数,先算整十数乘一位数的积,再算一位数乘一位数的积,最后把两次乘得的积相加。
备知识讲解
知识点 多位数乘一位数(不进位)的笔算方法
问题(1)导入 怎样算一共有多少支彩笔?(教材60页例1)
过程讲解
1.观图、读题,整理数学信息
已知条件 有3盒彩笔,每盒有12支。
所求问题 一共有多少支彩笔?
2.理解题意并列式
求一共有多少支彩笔,就是求3个12是多少,用乘法计算,列式为12×3。
3.探究12×3的计算方法
(1)口算。
方法一 利用加法口算。
12×3=12+12+12=36
方法二 利用数的组成口算。
10×3=30 2×3=6 30+6=36
(2)笔算。
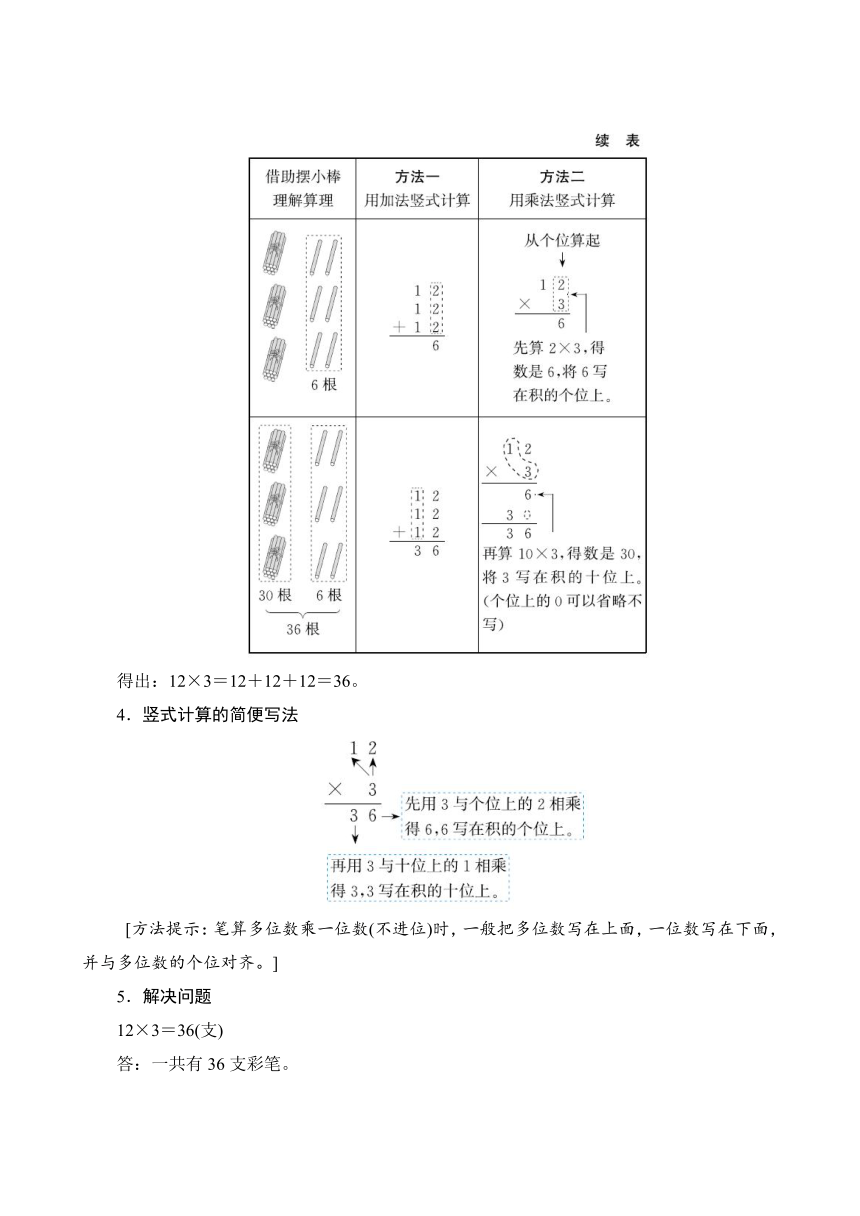
得出:12×3=12+12+12=36。
4.竖式计算的简便写法
[方法提示:笔算多位数乘一位数(不进位)时,一般把多位数写在上面,一位数写在下面,并与多位数的个位对齐。]
5.解决问题
12×3=36(支)
答:一共有36支彩笔。
问题(2)导入 笔算下面各题。
123×3= 4324×2=
过程讲解
1.方法分析
笔算方法与12×3的笔算方法相同,都是用一位数依次去乘多位数每一位上的数。
2.解决问题
123×3=369 4324×2=8648
[灵活运用:任何一个多位数乘一位数的乘法都可以用竖式计算。]
归纳总结
多位数乘一位数(不进位)的笔算方法:
相同数位对齐→把一位数写在多位数的下面,并与多位数的个位对齐。
从个位乘起→用一位数依次去乘多位数每一位上的数。
确定积的位置→一位数与多位数哪一位上的数相乘,就在横线下面对着那一位写积。
备易错易混
误区计算:23×3。
错误解答 23×3=96
错解改正 23×3=69
错解分析 此题错在把乘数3与第一个乘数十位上的2对齐了,且每次相乘的积也没有写在对应的数位上。
温馨提示
用竖式计算多位数乘一位数时,相同数位要对齐,从个位乘起。一位数与多位数哪一位上的数相乘,就在横线下面对着那一位写积。
备综合能力
思维开放 运用分析法或画线段图法解决倍数问题
典型例题 果园里有苹果树112棵,桃树的棵数是苹果树棵数的3倍。果园里苹果树和桃树一共有多少棵?
思路分析 思路一 分析法。
思路二 画线段图法。
借助线段图分析苹果树与桃树之间的数量关系,如下图:
由线段图可知,苹果树和桃树的总棵数正好是苹果树棵数的(1+3)倍,因此可以利用倍数关系求出苹果树和桃树的总棵数。
正确解答 方法一 112×3=336(棵)
112+336=448(棵)
方法二 1+3=4 112×4=448(棵)
答:果园里苹果树和桃树一共有448棵。
方法总结
解决倍数问题的关键是先明确谁是1倍数,谁是几倍数,再根据已知条件和所求问题画出线段图,借助线段图解题。
方法运用 运用推理法解决填数问题
典型例题 按规律填数。
3、5、9、17、33、( )。
思路分析 观察这组数可以发现,从第二个数开始,后面的数都比它前面的数的2倍少1,即5=3×2-1,9=5×2-1,17=9×2-1,33=17×2-1,根据找出的规律可以得出括号里的数应比33的2倍少1。
正确解答 65
方法总结
解决按规律填数问题时,要先找出相邻两个数之间的关系,总结出规律,再按规律填数。
备教学资源
用格子乘法计算两位数乘两位数
首先,写出要计算的数,按照数的位数画格子。如计算37×42,就画出4个格子(如下图),并在格子中向左下方画出斜线。然后在格子的上侧写上3、7,右侧写上4、2。
(1)将每个格子右侧和上侧的数相乘。7×4=28,将28写在格子内斜线的两侧(如下图)。
7×2,3×4,3×2的处理方法与上面相同,结果如下图。
(2)按照斜线方向,将格子里的数从右上向左下相加,结果写在外面。如果相加的结果超过10,就要向前一位进1。
(3)将格子外面的数从左上向右下按照顺序排列,答案就是1554。
备教材内容
本课时学习的是教材60页的内容及相关习题。本课时的学习建立在学生知道了乘法算式各部分的名称、掌握了表内乘法、整十、整百数乘一位数和两位数乘一位数(不进位)的口算方法等基础之上。本课时的内容是本单元教学的重点,同时也是继续学习多位数乘法的基础。教材创设了生活中的实际情境,从解决问题入手,体现了计算的实用价值。在计算中,体现算法多样化,呈现连加、口算和列乘法竖式计算等多种算法。呈现乘法竖式的几个环节,重点教学乘法竖式的笔算方法,让学生经历乘法竖式形成的过程,理解乘法竖式计算中每一步的算理,掌握算法。另外教材安排了做一做两道有层次性的对比练习,既为了正确书写竖式,同时也进一步巩固了笔算方法。
备教法学法
从素质教育着眼来看,要贯彻传授知识与培养能力相结合的原则,不仅要使学生学会知识,更要使学生会学、乐学、自主去学。
为了充分发挥学生的主体地位,使他们能够自主学习,切实提高课堂教学效率。采用谈话激趣、自主尝试、讨论归纳、强化练习等教学方法,循循诱导,让学生在尝试、迁移、类推、合作中自主学习,巩固和拓展所学知识。
教学目标
1、能够比较熟练地口算整十、整百、整千数乘一位数,两位数乘一位数(不进位)。
2、通过对比辨析,总结概括口算的计算方法,进一步理解算理,掌握算法。
3、能够运用所学知识,解决生活中的简单问题,提高解决问题的能力。
教学重难点
教学重点:
感受口算乘法的算法优化。
教学难点:
掌握口算乘法的方法。
备已学知识
1.整十、整百数乘一位数的口算方法:先把整十、整百数后面的0去掉,再相乘,计算出积后,在积的末尾添上之前去掉的0。
2.两位数乘一位数(不进位)的口算方法:把两位数分成整十数和一位数,先算整十数乘一位数的积,再算一位数乘一位数的积,最后把两次乘得的积相加。
备知识讲解
知识点 多位数乘一位数(不进位)的笔算方法
问题(1)导入 怎样算一共有多少支彩笔?(教材60页例1)
过程讲解
1.观图、读题,整理数学信息
已知条件 有3盒彩笔,每盒有12支。
所求问题 一共有多少支彩笔?
2.理解题意并列式
求一共有多少支彩笔,就是求3个12是多少,用乘法计算,列式为12×3。
3.探究12×3的计算方法
(1)口算。
方法一 利用加法口算。
12×3=12+12+12=36
方法二 利用数的组成口算。
10×3=30 2×3=6 30+6=36
(2)笔算。
得出:12×3=12+12+12=36。
4.竖式计算的简便写法
[方法提示:笔算多位数乘一位数(不进位)时,一般把多位数写在上面,一位数写在下面,并与多位数的个位对齐。]
5.解决问题
12×3=36(支)
答:一共有36支彩笔。
问题(2)导入 笔算下面各题。
123×3= 4324×2=
过程讲解
1.方法分析
笔算方法与12×3的笔算方法相同,都是用一位数依次去乘多位数每一位上的数。
2.解决问题
123×3=369 4324×2=8648
[灵活运用:任何一个多位数乘一位数的乘法都可以用竖式计算。]
归纳总结
多位数乘一位数(不进位)的笔算方法:
相同数位对齐→把一位数写在多位数的下面,并与多位数的个位对齐。
从个位乘起→用一位数依次去乘多位数每一位上的数。
确定积的位置→一位数与多位数哪一位上的数相乘,就在横线下面对着那一位写积。
备易错易混
误区计算:23×3。
错误解答 23×3=96
错解改正 23×3=69
错解分析 此题错在把乘数3与第一个乘数十位上的2对齐了,且每次相乘的积也没有写在对应的数位上。
温馨提示
用竖式计算多位数乘一位数时,相同数位要对齐,从个位乘起。一位数与多位数哪一位上的数相乘,就在横线下面对着那一位写积。
备综合能力
思维开放 运用分析法或画线段图法解决倍数问题
典型例题 果园里有苹果树112棵,桃树的棵数是苹果树棵数的3倍。果园里苹果树和桃树一共有多少棵?
思路分析 思路一 分析法。
思路二 画线段图法。
借助线段图分析苹果树与桃树之间的数量关系,如下图:
由线段图可知,苹果树和桃树的总棵数正好是苹果树棵数的(1+3)倍,因此可以利用倍数关系求出苹果树和桃树的总棵数。
正确解答 方法一 112×3=336(棵)
112+336=448(棵)
方法二 1+3=4 112×4=448(棵)
答:果园里苹果树和桃树一共有448棵。
方法总结
解决倍数问题的关键是先明确谁是1倍数,谁是几倍数,再根据已知条件和所求问题画出线段图,借助线段图解题。
方法运用 运用推理法解决填数问题
典型例题 按规律填数。
3、5、9、17、33、( )。
思路分析 观察这组数可以发现,从第二个数开始,后面的数都比它前面的数的2倍少1,即5=3×2-1,9=5×2-1,17=9×2-1,33=17×2-1,根据找出的规律可以得出括号里的数应比33的2倍少1。
正确解答 65
方法总结
解决按规律填数问题时,要先找出相邻两个数之间的关系,总结出规律,再按规律填数。
备教学资源
用格子乘法计算两位数乘两位数
首先,写出要计算的数,按照数的位数画格子。如计算37×42,就画出4个格子(如下图),并在格子中向左下方画出斜线。然后在格子的上侧写上3、7,右侧写上4、2。
(1)将每个格子右侧和上侧的数相乘。7×4=28,将28写在格子内斜线的两侧(如下图)。
7×2,3×4,3×2的处理方法与上面相同,结果如下图。
(2)按照斜线方向,将格子里的数从右上向左下相加,结果写在外面。如果相加的结果超过10,就要向前一位进1。
(3)将格子外面的数从左上向右下按照顺序排列,答案就是1554。
