6.3《多位数乘一位数(一次进位)的笔算乘法》(教案)-三年级 上册数学人教版
文档属性
| 名称 | 6.3《多位数乘一位数(一次进位)的笔算乘法》(教案)-三年级 上册数学人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 446.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 21:55:48 | ||
图片预览


文档简介
《多位数乘一位数(一次进位)的笔算乘法》教学设计
备教材内容
1.本课时学习的是教材61页的内容及相关习题。多位数乘一位数(一次进位)的笔算乘法是在学生掌握了多位数乘一位数(不进位)的笔算乘法的基础上进行教学的,学好本课时内容为后面学习多位数乘一位数间隔进位和连续进位奠定基础。
2.教材呈现了三个层次的内容:第一层次,教材选取了“王老师买连环画”的问题情境,这样的问题情境没有摆成叙述状的形式,旨在让学生主动收集数学信息,并经过自己的语言组织叙述出来,让学生思考怎样列式解决。这也是计算教学的一个重要方面,根据意义来列式解决。第二层次,教材通过直观操作,将动作表征转化为符号表征,突出教学难点。在学习时,借助小棒图帮助学生理解算理,一面操作小棒,一面叙述过程,同时用竖式记录每一步的操作过程。第三层次,下面“做一做”中,分别练习满十进1、满二十进2和三位数乘一位数(一次进位)的题目。每个小题都是一个类别,为学生能力的拓展提供了较大的空间。教材这样安排,不仅有助于学生借助直观操作理解算理,同时也培养了学生转化和迁移类推的能力。
备教法学法
本课时着重让学生通过自主探究的学习方式来探索计算方法。学生在学习中,可凭借已有的知识和经验大胆尝试,积累感性认识,理解进位的基本原理。通过试一试、摆一摆、说一说、比一比等数学活动,在“满十进1”的基础上,类推出“满几十进几”的算法。通过这样的教学,有助于学生掌握自主学习的方法,发展学生迁移类推的能力。
教学目标
1.经历探究多位数乘一位数(不连续进位)的笔算方法的过程,掌握多位数乘一位数(不连续进位)的笔算方法。
2.在计算的过程中理解竖式中每一步的含义,理解满几十进几的算理,并尝试总结计算方法,发展运算能力。
3.培养认真计算的习惯,提高解决问题的能力。
教学重难点
重点:掌握多位数乘一位数(不连续进位)的笔算方法。
难点:理解多位数乘一位数(不连续进位)的笔算算理。
备已学知识
1.口算乘法:整十、整百数乘一位数和两位数乘一位数(不进位)的口算。
2.多位数乘一位数(不进位)的笔算乘法:相同数位对齐,从个位乘起,用一位数依次去乘多位数每一位上的数,乘到哪一位,积就写在那一位的下面。
备知识讲解
知识点 多位数乘一位数(不连续进位)的笔算方法
问题(1)导入 一套连环画16本,王老师一共买了多少本连环画?(教材61页例2)
过程讲解
1.观图、读题,整理数学信息
已知条件 一套连环画16本,王老师买了3套。
所求问题 王老师一共买了多少本连环画?
2.理解题意并列式
求王老师一共买了多少本连环画,就是求3个16是多少,用乘法计算,列式为16×3。
3.探究16×3的计算方法,并理解算理
方法一 利用数的组成口算。
先把16分成10和6,再将10和6分别与3相乘,最后把两次相乘的积加起来。
所以16×3=48。
方法二 借助摆小棒列竖式计算。
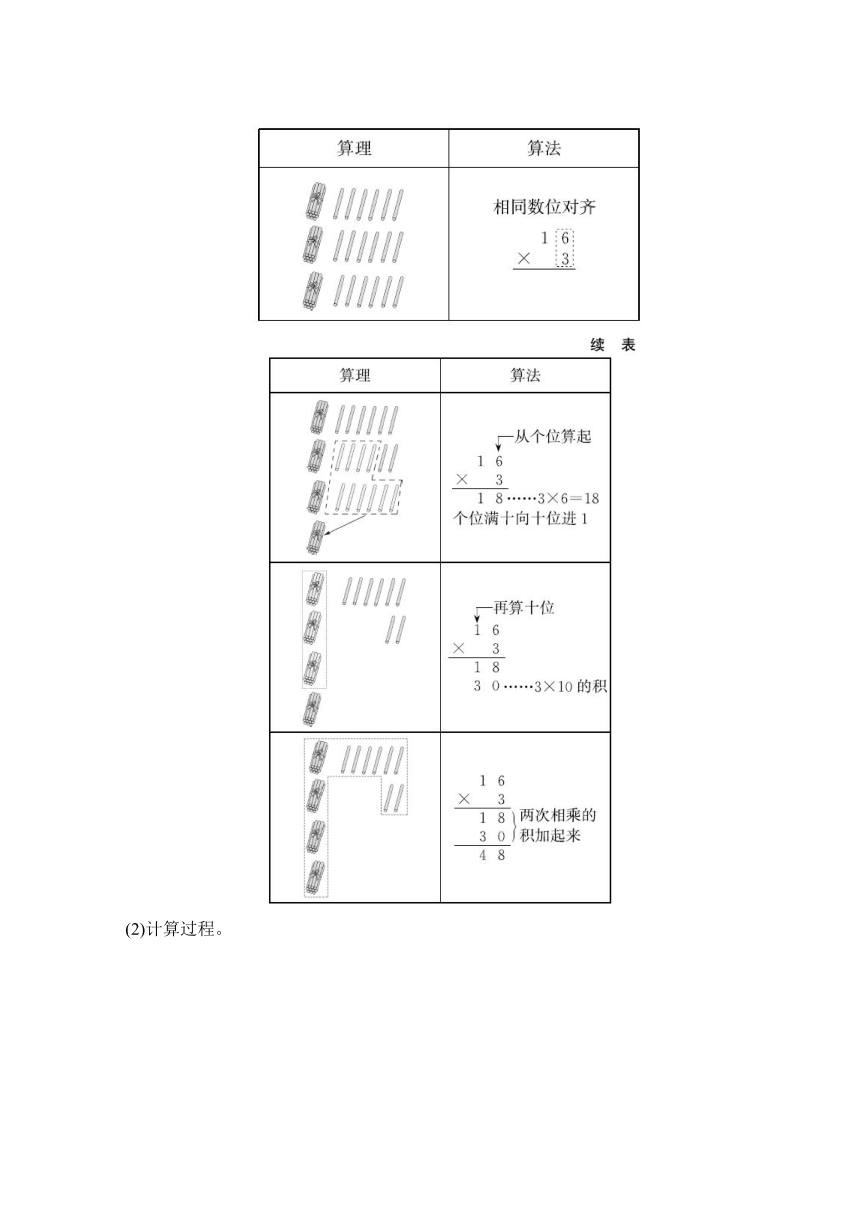
(1)理解算理,明确算法。
(2)计算过程。
[方法提示:笔算两位数乘一位数时,个位数相乘满几十,就要向十位进几(进位数写在个位和十位之间),十位乘完后不要忘记加上个位进上来的数。]
方法比较:列竖式计算比较简单,且不容易出错。
4.解决问题
16×3=48(本)
答:王老师一共买了48本连环画。
问题(2)导入 计算:214×3。
过程讲解
1.方法分析
三位数乘一位数的笔算方法与两位数乘一位数的笔算方法相同。
2.计算过程
214×3=642
归纳总结
多位数乘一位数(不连续进位)的笔算方法:先将一位数与多位数的个位对齐,再从个位乘起,哪一位相乘满几十就要向前一位进几。
知识巧记
笔算乘法并不难,数位对齐是关键。
个位起,依次乘,积满几十就进几。
后面进位前面加,进位之数别落下。
备易错易混
误区一计算:23×4。
错误解答 23×4=82
错解改正 23×4=92
错解分析 此题错在个位数相乘满十没有向十位进1,导致计算结果错误。
温馨提示
列竖式计算多位数乘一位数时,哪一位相乘满几十就要向前一位进几。
误区二判断:
2×8的积一定是三位数。(√)
错解分析 如果“2”的十位是1,那么原式就是12×8,12×8=96,积是两位数。
错解改正 ×
温馨提示
两位数乘一位数,积可能是两位数,也可能是三位数。
备综合能力
方法运用 运用推理法解决乘法竖式谜问题
典型例题 在□里填上合适的数字,满足个位数相乘满十向十位进1的要求。
思路分析 由题可知,□里的数字要满足与3相乘满十向十位进1的要求。
只有“2”的□里填4、5或6时,才能满足与3相乘满十向十位进1的要求。
正确解答
方法总结
解决此类题要明确题目要求,运用表内乘法确定满足条件的所有答案,考虑要全面,不能遗漏答案。
规律运用 运用移多补少法解决求连续自然数的和的问题
典型例题 在□里填上合适的数。
13+14+15+16+17
=15×□
=□
思路分析 观察算式中的5个连续自然数,发现只有把原式转化为几个相同加数相加的形式,才能写出乘法算式。运用移多补少法可以把这些加数都转化为15,如下所示:
由此可知,原式可以转化为15×5进行计算。
正确解答 13+14+15+16+17
=15×
=
规律总结
奇数个连续自然数的和等于正中间的加数乘加数的个数。
备教学资源
四则运算的起源
四则运算的起源很早,有的几乎与数字同时产生,如罗马数字6写成VI,即5加1的意思,4写成IV,即5减1的意思。在中国古代,四则运算很早就有了。战国时期的李悝(kuī)编写的一部有关法律方面的著作—— 《法经》中已有加、减、乘等运算,甚至还有除法运算。
陈景润
数学家陈景润,中国科学院院士,1933年5月22日生于福建省福州市仓山区,1953年毕业于厦门大学数学系。1957年进入中国科学院数学研究所,并在华罗庚教授的指导下从事数论方面的研究。曾任中国科学院数学研究所研究员、学术委员会委员兼贵阳民族学院、河南大学、青岛大学、福建师范大学等校教授,国家科委数学学科组成员,《数学季刊》主编等职。主要从事解析数论方面的研究,并在哥德巴赫猜想研究方面取得国际领先成果。这一成果国际上誉为“陈氏定理”,并受到广泛引用。
备教材内容
1.本课时学习的是教材61页的内容及相关习题。多位数乘一位数(一次进位)的笔算乘法是在学生掌握了多位数乘一位数(不进位)的笔算乘法的基础上进行教学的,学好本课时内容为后面学习多位数乘一位数间隔进位和连续进位奠定基础。
2.教材呈现了三个层次的内容:第一层次,教材选取了“王老师买连环画”的问题情境,这样的问题情境没有摆成叙述状的形式,旨在让学生主动收集数学信息,并经过自己的语言组织叙述出来,让学生思考怎样列式解决。这也是计算教学的一个重要方面,根据意义来列式解决。第二层次,教材通过直观操作,将动作表征转化为符号表征,突出教学难点。在学习时,借助小棒图帮助学生理解算理,一面操作小棒,一面叙述过程,同时用竖式记录每一步的操作过程。第三层次,下面“做一做”中,分别练习满十进1、满二十进2和三位数乘一位数(一次进位)的题目。每个小题都是一个类别,为学生能力的拓展提供了较大的空间。教材这样安排,不仅有助于学生借助直观操作理解算理,同时也培养了学生转化和迁移类推的能力。
备教法学法
本课时着重让学生通过自主探究的学习方式来探索计算方法。学生在学习中,可凭借已有的知识和经验大胆尝试,积累感性认识,理解进位的基本原理。通过试一试、摆一摆、说一说、比一比等数学活动,在“满十进1”的基础上,类推出“满几十进几”的算法。通过这样的教学,有助于学生掌握自主学习的方法,发展学生迁移类推的能力。
教学目标
1.经历探究多位数乘一位数(不连续进位)的笔算方法的过程,掌握多位数乘一位数(不连续进位)的笔算方法。
2.在计算的过程中理解竖式中每一步的含义,理解满几十进几的算理,并尝试总结计算方法,发展运算能力。
3.培养认真计算的习惯,提高解决问题的能力。
教学重难点
重点:掌握多位数乘一位数(不连续进位)的笔算方法。
难点:理解多位数乘一位数(不连续进位)的笔算算理。
备已学知识
1.口算乘法:整十、整百数乘一位数和两位数乘一位数(不进位)的口算。
2.多位数乘一位数(不进位)的笔算乘法:相同数位对齐,从个位乘起,用一位数依次去乘多位数每一位上的数,乘到哪一位,积就写在那一位的下面。
备知识讲解
知识点 多位数乘一位数(不连续进位)的笔算方法
问题(1)导入 一套连环画16本,王老师一共买了多少本连环画?(教材61页例2)
过程讲解
1.观图、读题,整理数学信息
已知条件 一套连环画16本,王老师买了3套。
所求问题 王老师一共买了多少本连环画?
2.理解题意并列式
求王老师一共买了多少本连环画,就是求3个16是多少,用乘法计算,列式为16×3。
3.探究16×3的计算方法,并理解算理
方法一 利用数的组成口算。
先把16分成10和6,再将10和6分别与3相乘,最后把两次相乘的积加起来。
所以16×3=48。
方法二 借助摆小棒列竖式计算。
(1)理解算理,明确算法。
(2)计算过程。
[方法提示:笔算两位数乘一位数时,个位数相乘满几十,就要向十位进几(进位数写在个位和十位之间),十位乘完后不要忘记加上个位进上来的数。]
方法比较:列竖式计算比较简单,且不容易出错。
4.解决问题
16×3=48(本)
答:王老师一共买了48本连环画。
问题(2)导入 计算:214×3。
过程讲解
1.方法分析
三位数乘一位数的笔算方法与两位数乘一位数的笔算方法相同。
2.计算过程
214×3=642
归纳总结
多位数乘一位数(不连续进位)的笔算方法:先将一位数与多位数的个位对齐,再从个位乘起,哪一位相乘满几十就要向前一位进几。
知识巧记
笔算乘法并不难,数位对齐是关键。
个位起,依次乘,积满几十就进几。
后面进位前面加,进位之数别落下。
备易错易混
误区一计算:23×4。
错误解答 23×4=82
错解改正 23×4=92
错解分析 此题错在个位数相乘满十没有向十位进1,导致计算结果错误。
温馨提示
列竖式计算多位数乘一位数时,哪一位相乘满几十就要向前一位进几。
误区二判断:
2×8的积一定是三位数。(√)
错解分析 如果“2”的十位是1,那么原式就是12×8,12×8=96,积是两位数。
错解改正 ×
温馨提示
两位数乘一位数,积可能是两位数,也可能是三位数。
备综合能力
方法运用 运用推理法解决乘法竖式谜问题
典型例题 在□里填上合适的数字,满足个位数相乘满十向十位进1的要求。
思路分析 由题可知,□里的数字要满足与3相乘满十向十位进1的要求。
只有“2”的□里填4、5或6时,才能满足与3相乘满十向十位进1的要求。
正确解答
方法总结
解决此类题要明确题目要求,运用表内乘法确定满足条件的所有答案,考虑要全面,不能遗漏答案。
规律运用 运用移多补少法解决求连续自然数的和的问题
典型例题 在□里填上合适的数。
13+14+15+16+17
=15×□
=□
思路分析 观察算式中的5个连续自然数,发现只有把原式转化为几个相同加数相加的形式,才能写出乘法算式。运用移多补少法可以把这些加数都转化为15,如下所示:
由此可知,原式可以转化为15×5进行计算。
正确解答 13+14+15+16+17
=15×
=
规律总结
奇数个连续自然数的和等于正中间的加数乘加数的个数。
备教学资源
四则运算的起源
四则运算的起源很早,有的几乎与数字同时产生,如罗马数字6写成VI,即5加1的意思,4写成IV,即5减1的意思。在中国古代,四则运算很早就有了。战国时期的李悝(kuī)编写的一部有关法律方面的著作—— 《法经》中已有加、减、乘等运算,甚至还有除法运算。
陈景润
数学家陈景润,中国科学院院士,1933年5月22日生于福建省福州市仓山区,1953年毕业于厦门大学数学系。1957年进入中国科学院数学研究所,并在华罗庚教授的指导下从事数论方面的研究。曾任中国科学院数学研究所研究员、学术委员会委员兼贵阳民族学院、河南大学、青岛大学、福建师范大学等校教授,国家科委数学学科组成员,《数学季刊》主编等职。主要从事解析数论方面的研究,并在哥德巴赫猜想研究方面取得国际领先成果。这一成果国际上誉为“陈氏定理”,并受到广泛引用。
