第1单元长方体和正方体精选题(单元测试)数学六年级上册苏教版(含解析)
文档属性
| 名称 | 第1单元长方体和正方体精选题(单元测试)数学六年级上册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-03 18:30:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1单元长方体和正方体精选题(单元测试)数学六年级上册苏教版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共18分)
1.下面的两个物体都是用相同的小正方体摆成的,两个物体的表面积相比,( )。
A.正方体大 B.长方体大 C.一样大 D.无法比较
2.下面4个图形中,( )不能折成一个无盖的正方体。
A. B. C. D.
3.小冬做测量“不规则物体体积”的实验,他先将一个石块放入棱长10厘米的正方体容器中,然后在容器中注满水,石块完全浸没,接着将石块取出,他发现容器里的水面下降了1.5厘米。这个石块的体积大约是( )立方厘米。
A.150 B.3 C.23 D.无法计算
4.一个正方体的棱长总和是48分米,它的表面积是( )。
A.64平方分米 B.96平方分米 C.144平方分米 D.72平方分米
5.一张纸长297毫米,宽210毫米。将100张纸叠起来,量得厚1厘米,一张纸的体积约是( )立方厘米。
A.60 B.6 C.0.6 D.0.06
6.用一根84厘米长的铁丝,能焊成长10厘米,宽6厘米,高( )厘米的长方体框架。
A.3 B.4 C.5 D.6
二、填空题(共20分)
7.在括号里填上合适的数或单位名称。
一个水桶的容积大约是12( ) 5.8立方分米=( )立方厘米
一张课桌的占地面积大约是24( ) 720( )=0.72( )
8.一个棱长为a厘米的正方体木块,把它平均分成两个大小完全相等的木块后,每小块木块的表面积是( )。
9.一个长方体木箱,从里面量得长6分米,宽4分米,高5分米。如果在木箱里放棱长是1分米的正方体包装盒,最多能放( )个。
10.将一个棱长4分米的正方体铁块,熔铸成一个横截面是边长为2分米的正方形的长方体,这个长方体的长是( )分米.
11.用一些棱长1厘米的小正方体木块摆一个物体,摆成的物体的体积是( )立方厘米。
前面看 上面看 侧面看
12.一个长方体,如果高增加2厘米就成了正方体,且体积增加了72立方厘米。原来这个长方体的体积是( )立方厘米。
三、判断题(共10分)
13.长方体一共有12条棱,可分为4组,每组有3条棱的长度相等。( )
14.长方体有两个相对的面是正方形,那么其余四个面都是正方形。( )
15.如果一个长方体的棱长总和是48cm,那么这个长方体相交于一个顶点的三条棱的长度之和是12cm。( )
16.把6个棱长是2厘米的正方体拼成长方体,这个长方体的表面积等于原来6个正方体的表面积之和。( )
17.计算一个长方体木箱的容积,要从木箱的里面量长、宽、高。( )
四、图形计算(共4分)
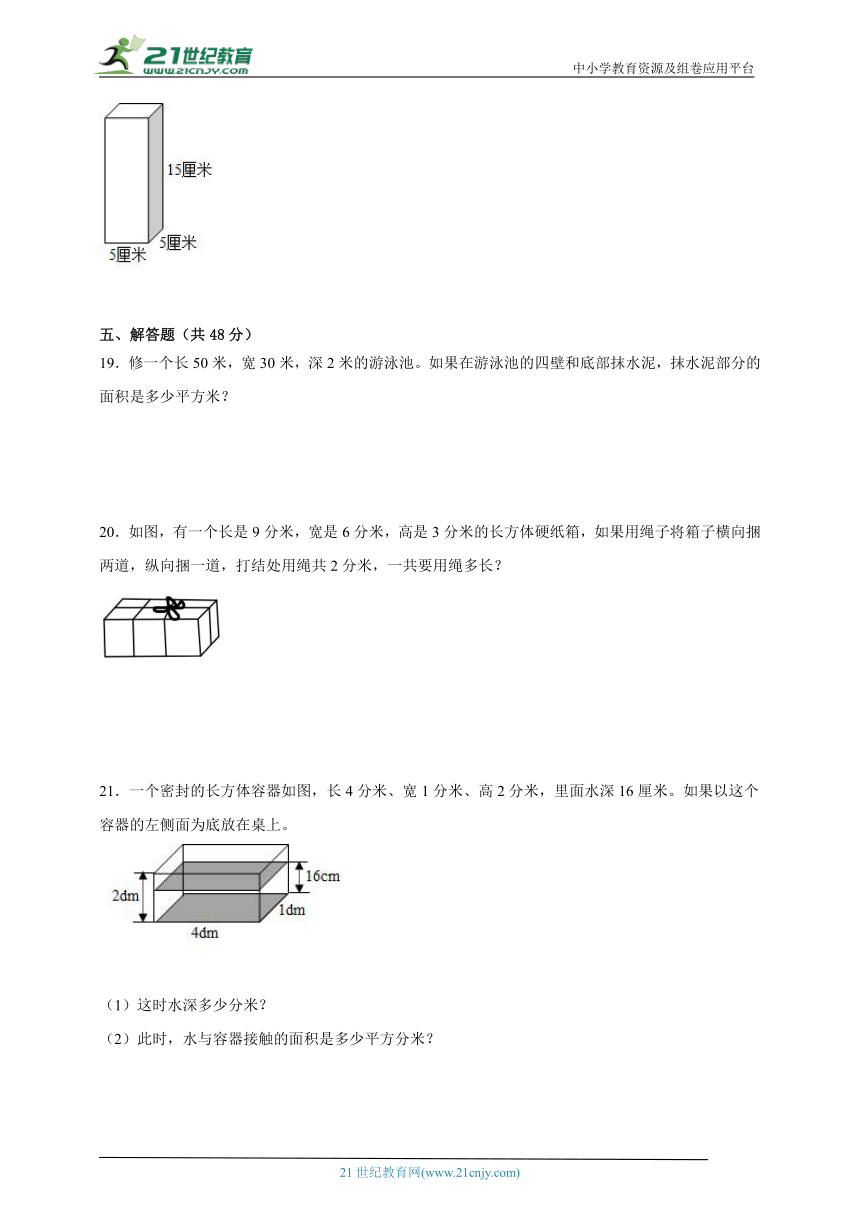
18.计算下面长方体的表面积。
五、解答题(共48分)
19.修一个长50米,宽30米,深2米的游泳池。如果在游泳池的四壁和底部抹水泥,抹水泥部分的面积是多少平方米?
20.如图,有一个长是9分米,宽是6分米,高是3分米的长方体硬纸箱,如果用绳子将箱子横向捆两道,纵向捆一道,打结处用绳共2分米,一共要用绳多长?
21.一个密封的长方体容器如图,长4分米、宽1分米、高2分米,里面水深16厘米。如果以这个容器的左侧面为底放在桌上。
(1)这时水深多少分米?
(2)此时,水与容器接触的面积是多少平方分米?
22.一根长的长方体木料,把它平均锯成3段,表面积正好增加,这根木料的体积是多少立方分米?
23.如果一个正方体的高减少3厘米,那么它的表面积就减少96平方厘米,原来正方体的体积是多少立方厘米?
24.如图:一个底面为正方形的长方体,把它的高减少3厘米后余下一个正方体,表面积比原来减少了60平方厘米,求原来长方体的体积。
参考答案:
1.A
【分析】假定小正方体的棱长是1,根据正方体表面积=棱长×棱长×6、长方体表面积=(长×宽+长×高+宽×高)×2,将数值代入求得各自的表面积,再比较大小即可。
【详解】假定小正方体的棱长是1。
正方体表面积:
正方体的表面积大。
故答案为:
【点睛】掌握长方体和正方体表面积计算公式是解答本题的关键。
2.D
【分析】无盖的正方体有5个面,根据正方体展开图的特征逐项分析。
【详解】A.符合无盖正方体展开图的特征,能折成一个无盖的正方体;
B.符合无盖正方体展开图的特征,能折成一个无盖的正方体;
C.符合无盖正方体展开图的特征,能折成一个无盖的正方体;
D.有两个面重合,折成的正方体缺少两个面,不能折成一个无盖的正方体。
故答案为:D
【点睛】根据正方体展开图的特征,运用空间想象力解决此类问题。
3.A
【分析】下降了1.5厘米的水的体积就是石块的体积。用10×10=100平方厘米,得到底面积,再用100×1.5即是石块的体积。据此解答。
【详解】10×10×1.5
=100×1.5
=150(立方厘米)
故答案为:A
【点睛】理解石块的体积就是下降1.5厘米的水的体积,再用议长方体体积公式进行计算是解答本题的关键。
4.B
【分析】由正方体的特征可知:正方体共有12条棱,且每条棱长都相等,棱长总和是48分米,则可以求出每条棱的长度,进而利用正方体的表面积公式就可以求出其表面积。
【详解】棱长:48÷12=4(分米)
正方体的表面积:
4×4×6
=16×6,
=96(平方分米)
故答案为:B
【点睛】解答此题的主要依据是:正方体共有12条棱长,且每条棱长都相等以及正方体的表面积公式。
5.B
【解析】将一张A4纸看成一个长方体,长是297毫米,宽是210毫米,高是1÷100厘米,将数据代入长方体体积公式:V=abh计算即可。
【详解】297毫米≈30厘米
210毫米≈20厘米
30×20×(1÷100)
=600×0.01
=6(立方厘米)
故答案为:B
【点睛】本题主要考查长方体体积公式的实际应用,解题时注意要将单位统一。
6.C
【分析】根据题意可知,这个长方体的棱长之和是84厘米,长方体的高=棱长之和÷4-(长+宽),把数据代入计算即可。
【详解】84÷4-(10+6)
=21-16
=5(厘米)
故答案为:C
【点睛】灵活运用长方体的棱长之和公式是解题的关键。
7. 升/L 5800 平方分米/dm2 立方厘米 立方分米
【分析】根据对容积单位、面积单位的认识及数据的大小可知:计量一个水桶的容积用升作单位;计量一张课桌的占地面积用平方分米作单位;1立方分米=1000立方厘米,高级单位换算成低级单位乘进率;720化为0.72相当于720÷1000,可填进率为1000的两个单位;据此解答。
【详解】一个水桶的容积大约是12升 5.8立方分米=5.8×1000立方厘米=5800立方厘米
一张课桌的占地面积大约是24平方分米 720立方厘米=0.72立方分米(最后一题答案不唯一)
【点睛】本题考查面积单位、容积单位的选择及体积单位的换算。
8.4a2
【分析】根据题意,把正方体分成两个大小完全相同的木块,分成两个相同的长方体,长方体的长是a厘米,宽是a厘米,高是a厘米,根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】(a×a+a×a+a×a)×2
=(a2+a2+a2)×2
=2a2×2
=4a2(平方厘米)
【点睛】本题考查长方体表面积公式的应用,关键明确分成长方体的高是正方体棱长的一半,长和宽和正方体的棱长相等。
9.120
【分析】先求出每条棱长上最多能放的块数,再借助长方体的体积公式进行计算即可解答。
【详解】以长为边最多放:6÷1=6(个)
以宽为边最多放:4÷1=4(个)
以高位边最多放:5÷1=5(个)
6×4×5
=24×5
=120(个)
【点睛】解答此题时不要用大体积除以小体积来计算块数。
10.16
【解析】略
11.7
【分析】根据观察题目中的三视图可知,下层5个分两排,前排有3个,后排有2个,靠左边,上层有2个,分别在下层的左边的前后排,据此可知一共有(5+2)个,再根据正方体的体积=棱长×棱长×棱长,用1×1×1即可求出一个小正方体的体积,进而用乘法求出总体积。
【详解】5+2=7(个)
1×1×1=1(立方厘米)
1×7=7(立方厘米)
摆成的物体的体积是7立方厘米。
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
12.144
【分析】根据题意可知:一个长方体如果高增加2厘米,就变成了一个正方体;说明长和宽相等且比高长2厘米;体积增加72立方厘米,据此可求出底面积72÷2=36(平方厘米),则长方体的长和宽均为36÷6=6(厘米),根据长方体的体积V=sh,,代入数值进行计算即可。
【详解】长方体底面积:72÷2=36(平方厘米)
长方体的长和宽:36÷6=6(厘米)
长方体的高:6-2=4(厘米)
长方体的体积:36×4=144(立方厘米)
【点睛】本题考查长方体体积公式的实际应用,关键是抓住长和宽相等且比高长2厘米这一数量关系。
13.×
【分析】根据长方体的特征:长方体有4条长,平行且相等;4条宽,平行且相等;4条高,平行且相等,判断即可。
【详解】长方体一共有12条棱,可以分为3组,每组有4条棱的长度相等,原说法错误。
故答案为:×
【点睛】根据长方体的特征,结合12条棱的分类进行解答即可。
14.×
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况下有两个相对的面是正方形),当长方体有两个相对的面是正方形时,其余四个面是面积相等,形状相同的长方形。据此判断。
【详解】根据长方体的特征,最多有两个相对的面是正方形,其余四个面都是长方形。
故答案为:×
【点睛】正确理解长方体的特征是解决此题的关键。
15.√
【分析】根据长方体棱长总和=(长+宽+高)×4即可求出长+宽+高的和,也就是长方体相交于一个顶点的三条棱的长度之和。
【详解】48÷4=12(cm)
故答案为:√
【点睛】此题主要考查学生对长方体棱长总和的理解与应用。
16.×
【分析】把6个棱长是2厘米的正方体拼成长方体,无论怎么拼,总有几个面拼到了长方体的里面,则6个正方体拼成长方体后,表面积减少。
【详解】把6个棱长是2厘米的正方体拼成长方体,露在外面的面数量减少,则这个长方体的表面积小于原来6个正方体的表面积之和。
故答案为:×
【点睛】本题考查立体图形的切拼。两个立体图形(比如正方体之间)拼起来,因为面的数目减少,所以表面积减少。
17.√
【分析】箱子、油桶等能容纳物体的体积叫做它们的容积。由于容器有一定的厚度,计算容积时,要从里面去测量。长方体的体积=长×宽×高。
【详解】计算一个长方体木箱的容积,由于箱子有厚度,所以要从木箱的里面量长、宽、高。
故答案为:√
【点睛】根据容积的意义和长方体的体积公式即可解答。
18.350平方厘米
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,把题中数据代入公式计算,据此解答。
【详解】(5×5+5×15+5×15)×2
=(25+75+75)×2
=175×2
=350(平方厘米)
所以,长方体的表面积是350平方厘米。
19.1820平方米
【分析】由于游泳池无盖,所以抹水泥部分的面积是这个长方体的一个底面和4个侧面的总面积,根据无盖长方体的表面积公式:S=ab+(ah+bh)×2,把数据代入公式解答。
【详解】50×30+(50×2+30×2)×2
=1500+(100+60)×2
=1500+160×2
=1500+320
=1820(平方米)
答:抹水泥部分的面积是1820平方米。
【点睛】此题主要考查学生对长方体的表面积的计算方法的灵活应用。
20.62分米
【分析】根据长方体的特征:12条棱分为互相平行的(相对的)3组,每组4条棱的长度相等。已知“用绳子将箱子横着捆两道,纵向捆一道,打结处共用2分米”,所用绳子的长度相当于6条高、4条宽、2条长,再加上打结处共用2分米;由此解答。
【详解】6×3+4×6+9×2+2
=18+24+18+2
=42+18+2
=60+2
=62(分米)
答:一共要用绳子62分米。
【点睛】此题考查的目的使学生掌握长方体的特征,根据长方体棱长总和的计算方法解答。
21.(1)3.2分米
(2)21.2平方分米
【分析】(1)根据长方体的体积公式V=abh,求出长方体容器内水的体积,由于容器内水的体积不变,把容器的左面作为底面,所以用水的体积除以左面那个面的底面积就是水面的高度;
(2)水与容器的接触面的面积就是长2分米,宽1分米,高为此时水深的长方体5个面的面积,缺少上面,根据长方体的表面积解答即可。
【详解】16厘米=1.6分米
(1)4×1×1.6=6.4(立方分米)
6.4÷(2×1)
=6.4÷2
=3.2(分米)
答:这时水深3.2分米。
(2)2×1+2×3.2×2+1×3.2×2
=2+12.8+6.4
=21.2(平方分米)
答:水与容器的接触面的面积是21.2平方分米。
【点睛】解答此题应抓住水的体积不变,用水的体积除以长方体容器的底面积(左面那个面的面积),就是水面的高度。
22.864立方分米
【分析】根据题意可知,锯的段数比锯的次数多1,锯成3段需要锯2次,每锯1次就增加两个截面,那么锯2次增加4个截面,已知锯后表面积比原来增加48平方分米,由此可以求出长方体木料的底面积,再根据长方体的体积公式:V=sh,代入数据计算即可。
【详解】(3-1)×2
=2×2
=4(个)
48÷4×72
=12×72
=864(立方分米)
答:这根长方体木料的体积是864立方分米。
【点睛】解答本题的关键是理解锯木问题锯的次数比锯的段数少1,先求出底面积,再根据长方体的体积公式v=sh,列式解答即可。
23.512立方厘米
【分析】根据题意可知,一个正方体的高减少3厘米,那么它的表面积就减少96平方厘米;因此减少的96平方厘米是4个同样的长方形的面积和;由此可以求每个长方形的面积,进而求出正方体的棱长再根据正方体的体积公式: v=a3,把数据代入公式解答。
【详解】96÷4÷3
=24÷3
=8(厘米)
8×8×8=512(立方厘米)
答:原来正方体的体积是512立方厘米。
【点睛】此题属于应用长方体表面积计算公式和正方体的体积计算公式解决实际问题,解答此题的关键是熟记并灵活运用长方体表面积公式、正方体的体积计算公式。
24.200立方厘米
【分析】根据高减少3厘米就剩下一个正方体可知,这个正方体比原长方体表面积减少的4个面是相同的,根据已知表面积减少60平方厘米;即:60÷4÷3=5(厘米),求出原长方体的宽,也就是剩下的正方体的棱长,然后求出原长方体的高为(5+3)厘米,再根据长方体的体积:V=abh,解答即可。
【详解】60÷4÷3=5(厘米)
5+3=8(厘米)
5×5×8=200(立方厘米)
答:原来长方体的体积是200立方厘米。
【点睛】熟练掌握正方体体积计算公式和长方体表面积计算公式,灵活运用,是解答此题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1单元长方体和正方体精选题(单元测试)数学六年级上册苏教版
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 四 五 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(共18分)
1.下面的两个物体都是用相同的小正方体摆成的,两个物体的表面积相比,( )。
A.正方体大 B.长方体大 C.一样大 D.无法比较
2.下面4个图形中,( )不能折成一个无盖的正方体。
A. B. C. D.
3.小冬做测量“不规则物体体积”的实验,他先将一个石块放入棱长10厘米的正方体容器中,然后在容器中注满水,石块完全浸没,接着将石块取出,他发现容器里的水面下降了1.5厘米。这个石块的体积大约是( )立方厘米。
A.150 B.3 C.23 D.无法计算
4.一个正方体的棱长总和是48分米,它的表面积是( )。
A.64平方分米 B.96平方分米 C.144平方分米 D.72平方分米
5.一张纸长297毫米,宽210毫米。将100张纸叠起来,量得厚1厘米,一张纸的体积约是( )立方厘米。
A.60 B.6 C.0.6 D.0.06
6.用一根84厘米长的铁丝,能焊成长10厘米,宽6厘米,高( )厘米的长方体框架。
A.3 B.4 C.5 D.6
二、填空题(共20分)
7.在括号里填上合适的数或单位名称。
一个水桶的容积大约是12( ) 5.8立方分米=( )立方厘米
一张课桌的占地面积大约是24( ) 720( )=0.72( )
8.一个棱长为a厘米的正方体木块,把它平均分成两个大小完全相等的木块后,每小块木块的表面积是( )。
9.一个长方体木箱,从里面量得长6分米,宽4分米,高5分米。如果在木箱里放棱长是1分米的正方体包装盒,最多能放( )个。
10.将一个棱长4分米的正方体铁块,熔铸成一个横截面是边长为2分米的正方形的长方体,这个长方体的长是( )分米.
11.用一些棱长1厘米的小正方体木块摆一个物体,摆成的物体的体积是( )立方厘米。
前面看 上面看 侧面看
12.一个长方体,如果高增加2厘米就成了正方体,且体积增加了72立方厘米。原来这个长方体的体积是( )立方厘米。
三、判断题(共10分)
13.长方体一共有12条棱,可分为4组,每组有3条棱的长度相等。( )
14.长方体有两个相对的面是正方形,那么其余四个面都是正方形。( )
15.如果一个长方体的棱长总和是48cm,那么这个长方体相交于一个顶点的三条棱的长度之和是12cm。( )
16.把6个棱长是2厘米的正方体拼成长方体,这个长方体的表面积等于原来6个正方体的表面积之和。( )
17.计算一个长方体木箱的容积,要从木箱的里面量长、宽、高。( )
四、图形计算(共4分)
18.计算下面长方体的表面积。
五、解答题(共48分)
19.修一个长50米,宽30米,深2米的游泳池。如果在游泳池的四壁和底部抹水泥,抹水泥部分的面积是多少平方米?
20.如图,有一个长是9分米,宽是6分米,高是3分米的长方体硬纸箱,如果用绳子将箱子横向捆两道,纵向捆一道,打结处用绳共2分米,一共要用绳多长?
21.一个密封的长方体容器如图,长4分米、宽1分米、高2分米,里面水深16厘米。如果以这个容器的左侧面为底放在桌上。
(1)这时水深多少分米?
(2)此时,水与容器接触的面积是多少平方分米?
22.一根长的长方体木料,把它平均锯成3段,表面积正好增加,这根木料的体积是多少立方分米?
23.如果一个正方体的高减少3厘米,那么它的表面积就减少96平方厘米,原来正方体的体积是多少立方厘米?
24.如图:一个底面为正方形的长方体,把它的高减少3厘米后余下一个正方体,表面积比原来减少了60平方厘米,求原来长方体的体积。
参考答案:
1.A
【分析】假定小正方体的棱长是1,根据正方体表面积=棱长×棱长×6、长方体表面积=(长×宽+长×高+宽×高)×2,将数值代入求得各自的表面积,再比较大小即可。
【详解】假定小正方体的棱长是1。
正方体表面积:
正方体的表面积大。
故答案为:
【点睛】掌握长方体和正方体表面积计算公式是解答本题的关键。
2.D
【分析】无盖的正方体有5个面,根据正方体展开图的特征逐项分析。
【详解】A.符合无盖正方体展开图的特征,能折成一个无盖的正方体;
B.符合无盖正方体展开图的特征,能折成一个无盖的正方体;
C.符合无盖正方体展开图的特征,能折成一个无盖的正方体;
D.有两个面重合,折成的正方体缺少两个面,不能折成一个无盖的正方体。
故答案为:D
【点睛】根据正方体展开图的特征,运用空间想象力解决此类问题。
3.A
【分析】下降了1.5厘米的水的体积就是石块的体积。用10×10=100平方厘米,得到底面积,再用100×1.5即是石块的体积。据此解答。
【详解】10×10×1.5
=100×1.5
=150(立方厘米)
故答案为:A
【点睛】理解石块的体积就是下降1.5厘米的水的体积,再用议长方体体积公式进行计算是解答本题的关键。
4.B
【分析】由正方体的特征可知:正方体共有12条棱,且每条棱长都相等,棱长总和是48分米,则可以求出每条棱的长度,进而利用正方体的表面积公式就可以求出其表面积。
【详解】棱长:48÷12=4(分米)
正方体的表面积:
4×4×6
=16×6,
=96(平方分米)
故答案为:B
【点睛】解答此题的主要依据是:正方体共有12条棱长,且每条棱长都相等以及正方体的表面积公式。
5.B
【解析】将一张A4纸看成一个长方体,长是297毫米,宽是210毫米,高是1÷100厘米,将数据代入长方体体积公式:V=abh计算即可。
【详解】297毫米≈30厘米
210毫米≈20厘米
30×20×(1÷100)
=600×0.01
=6(立方厘米)
故答案为:B
【点睛】本题主要考查长方体体积公式的实际应用,解题时注意要将单位统一。
6.C
【分析】根据题意可知,这个长方体的棱长之和是84厘米,长方体的高=棱长之和÷4-(长+宽),把数据代入计算即可。
【详解】84÷4-(10+6)
=21-16
=5(厘米)
故答案为:C
【点睛】灵活运用长方体的棱长之和公式是解题的关键。
7. 升/L 5800 平方分米/dm2 立方厘米 立方分米
【分析】根据对容积单位、面积单位的认识及数据的大小可知:计量一个水桶的容积用升作单位;计量一张课桌的占地面积用平方分米作单位;1立方分米=1000立方厘米,高级单位换算成低级单位乘进率;720化为0.72相当于720÷1000,可填进率为1000的两个单位;据此解答。
【详解】一个水桶的容积大约是12升 5.8立方分米=5.8×1000立方厘米=5800立方厘米
一张课桌的占地面积大约是24平方分米 720立方厘米=0.72立方分米(最后一题答案不唯一)
【点睛】本题考查面积单位、容积单位的选择及体积单位的换算。
8.4a2
【分析】根据题意,把正方体分成两个大小完全相同的木块,分成两个相同的长方体,长方体的长是a厘米,宽是a厘米,高是a厘米,根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,代入数据,即可解答。
【详解】(a×a+a×a+a×a)×2
=(a2+a2+a2)×2
=2a2×2
=4a2(平方厘米)
【点睛】本题考查长方体表面积公式的应用,关键明确分成长方体的高是正方体棱长的一半,长和宽和正方体的棱长相等。
9.120
【分析】先求出每条棱长上最多能放的块数,再借助长方体的体积公式进行计算即可解答。
【详解】以长为边最多放:6÷1=6(个)
以宽为边最多放:4÷1=4(个)
以高位边最多放:5÷1=5(个)
6×4×5
=24×5
=120(个)
【点睛】解答此题时不要用大体积除以小体积来计算块数。
10.16
【解析】略
11.7
【分析】根据观察题目中的三视图可知,下层5个分两排,前排有3个,后排有2个,靠左边,上层有2个,分别在下层的左边的前后排,据此可知一共有(5+2)个,再根据正方体的体积=棱长×棱长×棱长,用1×1×1即可求出一个小正方体的体积,进而用乘法求出总体积。
【详解】5+2=7(个)
1×1×1=1(立方厘米)
1×7=7(立方厘米)
摆成的物体的体积是7立方厘米。
【点睛】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
12.144
【分析】根据题意可知:一个长方体如果高增加2厘米,就变成了一个正方体;说明长和宽相等且比高长2厘米;体积增加72立方厘米,据此可求出底面积72÷2=36(平方厘米),则长方体的长和宽均为36÷6=6(厘米),根据长方体的体积V=sh,,代入数值进行计算即可。
【详解】长方体底面积:72÷2=36(平方厘米)
长方体的长和宽:36÷6=6(厘米)
长方体的高:6-2=4(厘米)
长方体的体积:36×4=144(立方厘米)
【点睛】本题考查长方体体积公式的实际应用,关键是抓住长和宽相等且比高长2厘米这一数量关系。
13.×
【分析】根据长方体的特征:长方体有4条长,平行且相等;4条宽,平行且相等;4条高,平行且相等,判断即可。
【详解】长方体一共有12条棱,可以分为3组,每组有4条棱的长度相等,原说法错误。
故答案为:×
【点睛】根据长方体的特征,结合12条棱的分类进行解答即可。
14.×
【分析】根据长方体的特征,长方体的6个面都是长方形(特殊情况下有两个相对的面是正方形),当长方体有两个相对的面是正方形时,其余四个面是面积相等,形状相同的长方形。据此判断。
【详解】根据长方体的特征,最多有两个相对的面是正方形,其余四个面都是长方形。
故答案为:×
【点睛】正确理解长方体的特征是解决此题的关键。
15.√
【分析】根据长方体棱长总和=(长+宽+高)×4即可求出长+宽+高的和,也就是长方体相交于一个顶点的三条棱的长度之和。
【详解】48÷4=12(cm)
故答案为:√
【点睛】此题主要考查学生对长方体棱长总和的理解与应用。
16.×
【分析】把6个棱长是2厘米的正方体拼成长方体,无论怎么拼,总有几个面拼到了长方体的里面,则6个正方体拼成长方体后,表面积减少。
【详解】把6个棱长是2厘米的正方体拼成长方体,露在外面的面数量减少,则这个长方体的表面积小于原来6个正方体的表面积之和。
故答案为:×
【点睛】本题考查立体图形的切拼。两个立体图形(比如正方体之间)拼起来,因为面的数目减少,所以表面积减少。
17.√
【分析】箱子、油桶等能容纳物体的体积叫做它们的容积。由于容器有一定的厚度,计算容积时,要从里面去测量。长方体的体积=长×宽×高。
【详解】计算一个长方体木箱的容积,由于箱子有厚度,所以要从木箱的里面量长、宽、高。
故答案为:√
【点睛】根据容积的意义和长方体的体积公式即可解答。
18.350平方厘米
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,把题中数据代入公式计算,据此解答。
【详解】(5×5+5×15+5×15)×2
=(25+75+75)×2
=175×2
=350(平方厘米)
所以,长方体的表面积是350平方厘米。
19.1820平方米
【分析】由于游泳池无盖,所以抹水泥部分的面积是这个长方体的一个底面和4个侧面的总面积,根据无盖长方体的表面积公式:S=ab+(ah+bh)×2,把数据代入公式解答。
【详解】50×30+(50×2+30×2)×2
=1500+(100+60)×2
=1500+160×2
=1500+320
=1820(平方米)
答:抹水泥部分的面积是1820平方米。
【点睛】此题主要考查学生对长方体的表面积的计算方法的灵活应用。
20.62分米
【分析】根据长方体的特征:12条棱分为互相平行的(相对的)3组,每组4条棱的长度相等。已知“用绳子将箱子横着捆两道,纵向捆一道,打结处共用2分米”,所用绳子的长度相当于6条高、4条宽、2条长,再加上打结处共用2分米;由此解答。
【详解】6×3+4×6+9×2+2
=18+24+18+2
=42+18+2
=60+2
=62(分米)
答:一共要用绳子62分米。
【点睛】此题考查的目的使学生掌握长方体的特征,根据长方体棱长总和的计算方法解答。
21.(1)3.2分米
(2)21.2平方分米
【分析】(1)根据长方体的体积公式V=abh,求出长方体容器内水的体积,由于容器内水的体积不变,把容器的左面作为底面,所以用水的体积除以左面那个面的底面积就是水面的高度;
(2)水与容器的接触面的面积就是长2分米,宽1分米,高为此时水深的长方体5个面的面积,缺少上面,根据长方体的表面积解答即可。
【详解】16厘米=1.6分米
(1)4×1×1.6=6.4(立方分米)
6.4÷(2×1)
=6.4÷2
=3.2(分米)
答:这时水深3.2分米。
(2)2×1+2×3.2×2+1×3.2×2
=2+12.8+6.4
=21.2(平方分米)
答:水与容器的接触面的面积是21.2平方分米。
【点睛】解答此题应抓住水的体积不变,用水的体积除以长方体容器的底面积(左面那个面的面积),就是水面的高度。
22.864立方分米
【分析】根据题意可知,锯的段数比锯的次数多1,锯成3段需要锯2次,每锯1次就增加两个截面,那么锯2次增加4个截面,已知锯后表面积比原来增加48平方分米,由此可以求出长方体木料的底面积,再根据长方体的体积公式:V=sh,代入数据计算即可。
【详解】(3-1)×2
=2×2
=4(个)
48÷4×72
=12×72
=864(立方分米)
答:这根长方体木料的体积是864立方分米。
【点睛】解答本题的关键是理解锯木问题锯的次数比锯的段数少1,先求出底面积,再根据长方体的体积公式v=sh,列式解答即可。
23.512立方厘米
【分析】根据题意可知,一个正方体的高减少3厘米,那么它的表面积就减少96平方厘米;因此减少的96平方厘米是4个同样的长方形的面积和;由此可以求每个长方形的面积,进而求出正方体的棱长再根据正方体的体积公式: v=a3,把数据代入公式解答。
【详解】96÷4÷3
=24÷3
=8(厘米)
8×8×8=512(立方厘米)
答:原来正方体的体积是512立方厘米。
【点睛】此题属于应用长方体表面积计算公式和正方体的体积计算公式解决实际问题,解答此题的关键是熟记并灵活运用长方体表面积公式、正方体的体积计算公式。
24.200立方厘米
【分析】根据高减少3厘米就剩下一个正方体可知,这个正方体比原长方体表面积减少的4个面是相同的,根据已知表面积减少60平方厘米;即:60÷4÷3=5(厘米),求出原长方体的宽,也就是剩下的正方体的棱长,然后求出原长方体的高为(5+3)厘米,再根据长方体的体积:V=abh,解答即可。
【详解】60÷4÷3=5(厘米)
5+3=8(厘米)
5×5×8=200(立方厘米)
答:原来长方体的体积是200立方厘米。
【点睛】熟练掌握正方体体积计算公式和长方体表面积计算公式,灵活运用,是解答此题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
