4.4.1对数函数的概念 课件(共20张PPT)
文档属性
| 名称 | 4.4.1对数函数的概念 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 21:37:49 | ||
图片预览






文档简介
(共20张PPT)
第4章 指数函数与对数函数
4.4 对数函数
4.4.1 对数函数的概念
人教A版(2019)
教学目标
学习目标 数学素养
1.理解对数函数的概念. 1.数学类比、数学抽象素养.
2.会求与对数函数有关的定义域问题. 2.数学运算素养
3.了解对数函数在生产实际中的简单应用. 3.数学建模素养.
温故知新
1.对数的定义
一般地, 如果ax=N(a>0, 且a≠1), 那么数x叫做以a为底N的对数, 记作 其中a叫做对数的底数, N叫做真数.
x = logaN ,
注意:0和负数没有对数;
2.对数与指数之间的关系
ax =N logaN = x
温故知新
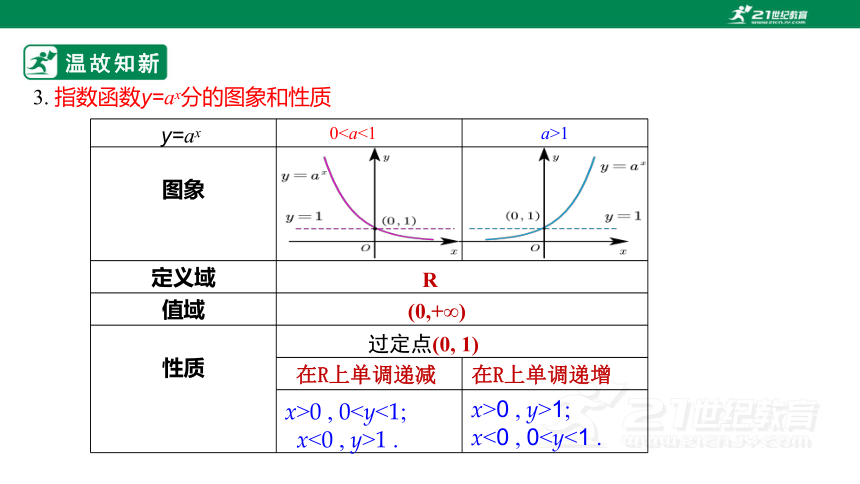
3. 指数函数y=ax分的图象和性质
图象
定义域 值域 性质
y=ax
0a>1
R
(0,+∞)
过定点(0, 1)
在R上单调递增
在R上单调递减
x>0 , 0x<0 , y>1 .
x>0 , y>1;
x<0 , 0新知导入
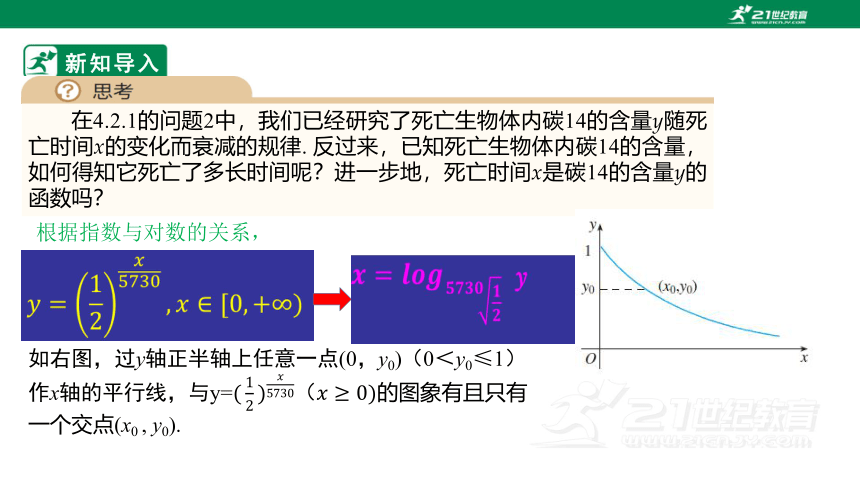
在4.2.1的问题2中,我们已经研究了死亡生物体内碳14的含量y随死亡时间x的变化而衰减的规律. 反过来,已知死亡生物体内碳14的含量,如何得知它死亡了多长时间呢?进一步地,死亡时间x是碳14的含量y的函数吗?
根据指数与对数的关系,
如右图,过y轴正半轴上任意一点(0,y0)(0<y0≤1)作x轴的平行线,与y=的图象有且只有一个交点(x0 , y0).
新知探究
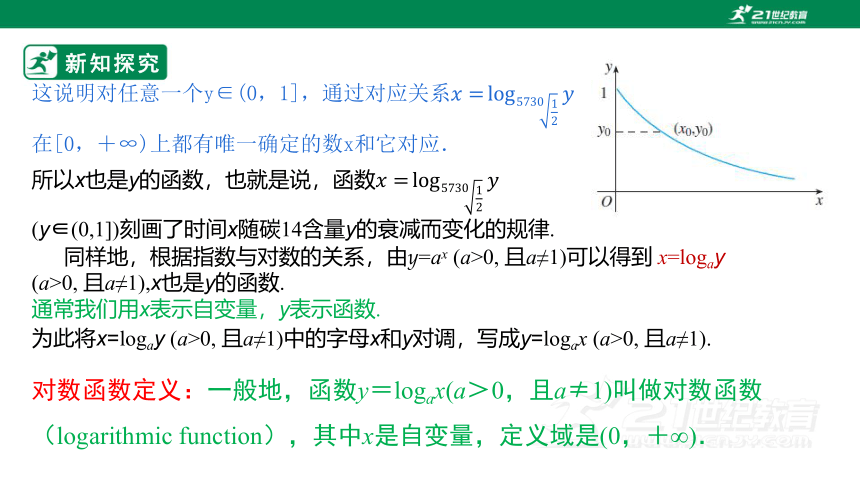
这说明对任意一个y∈(0,1],通过对应关系在[0,+∞)上都有唯一确定的数x和它对应.
所以x也是y的函数,也就是说,函数 (y∈(0,1])刻画了时间x随碳14含量y的衰减而变化的规律.
同样地,根据指数与对数的关系,由y=ax (a>0, 且a≠1)可以得到 x=logay (a>0, 且a≠1),x也是y的函数.
通常我们用x表示自变量,y表示函数.
为此将x=logay (a>0, 且a≠1)中的字母x和y对调,写成y=logax (a>0, 且a≠1).
对数函数定义:一般地,函数y=logax(a>0,且a≠1)叫做对数函数(logarithmic function),其中x是自变量,定义域是(0,+∞).
新知探究
想一想
(1)对数函数的定义域为什么是(0,+∞)
(2)对数函数的解析式有何特征?
(1)ax=N logaN=x,真数为幂值N,而N>0,故式子logax中,x>0.
(2)①a>0,且a≠1;②logax的系数为1;③自变量x的系数为1.
注意:在对数函数y=logax中,
①a>0,且a≠1;
②x∈(0,+∞);
③必须符合对数函数的三个特征.
新知讲授
概念辨析:下列函数表达式中,是对数函数的有( )
①y=logx2; ②y=logax(a∈R); ③y=log8x; ④y=lnx;
⑤y=logx(x+2);⑥y=2log4x; ⑦y=log2(x+1).
A.1个 B.2个 C.3个 D.4个
解析:
①中自变量出现在底数上,∴①不是对数函数;
②中底数a∈R不能保证a>0且a≠1;
⑤、⑦的真数分别为(x+2),(x+1);
⑥中log4x系数为2;
只有③、④符合对数函数的定义.故选B.
B
新知讲解
【例1】求下列函数的定义域:
(1) y=log3x2; (2) y=loga(4-x) (a>0, 且a≠1);
解:
(1)∵即
∴函数的定义域是
(2)∵即
∴的定义域是
新知讲解
求对数型函数定义域的原则:
(1)分母不能为0;
(2)根指数为偶数时,被开方数非负;
(3)对数的真数大于0,底数大于0且不为1;
(4)若需对函数进行变形,则需先求出定义域,再对函数进行恒等变形.
初试身手
1.求下列函数的定义域:
解:
(2)∵,解得.
(3)∵,解得.
(1) y=ln(1-x);
⑵y=;
⑶ .
∴函数y=ln(1-x)的定义域是
(1)∵1-x>0 , 即x<1,
∴函数y=的定义域是
∴函数的定义域是
新知讲解
【例2】假设某地初始物价为1, 每年以5%的增长率递增,经过y年后的物价为x.
(1)该地的物价经过几年后会翻一番?
(2)填写下表,并根据表中的数据, 说明该地物价的变化规律.
解:
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
(1)由题意可知,经过y年后物价x为
x=(1+5%)y ,
即x=1.05y (y∈[0,+∞))
由对数与指数间的关系,可得
y=log1.05x (x∈[1, +∞)).
由计算工具可得,当x=2时,y≈14.
所以,该地区的物价大约经过14年后会翻一番.
新知讲解
【例2】假设某地初始物价为1, 每年以5%的增长率递增,经过y年后的物价为x.
(1)该地的物价经过几年后会翻一番?
(2)填写下表,并根据表中的数据, 说明该地物价的变化规律.
解:
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
(2)根据函数y=log1.05x (x∈[1, +∞)),利用计算工具,可得
数据表明该地区的物价随时间增长而增长,但大约每增加1倍所需要的时间在逐渐缩小.
14
23
28
33
37
40
43
45
47
初试身手
解析:当时,,当λ时,,
∴=1+0.6,∴λ=1579.故选C.
2.我国的5G通信技术领先世界,5G技术的数学原理之一是著名的香农(Shannon)公式,香农提出并严格证明了“在被高斯白噪声干扰的信道中,计算最大信息传送速率C的公式 C= ,其中W是信道带宽(赫兹),S是信道内所传信号的平均功率(瓦),N是信道内部的高斯噪声功率(瓦),其中叫做信噪比.根据此公式,在不改变W的前提下,将信噪比从99提升至λ,使得C大约增加了60%,则λ的值大约为( ) (参考数据:100.2≈1.58)
A.1 559 B.3 943 C.1 579 D.2 512
C
拓展延申
求下列函数的定义域:
⑴f(x)= ; ⑵f(x)=;
⑶f(x)=.
解:
解得x>0且x≠1,
所以此函数的定义域为{x|x>0且x≠1}.
⑴要使函数有意义,必有,
⑵要使函数有意义,必有(3-x)(3+x)>0,
解得-3所以此函数的定义域为(-3,3).
⑶要使函数有意义,必有,
解得0所以此函数的定义域为(0,2].
课堂小结
2.求与对数函数有关的函数的定义域.
3.对数函数模型问题的求解.
1.对数函数定义:一般地,函数y=logax(a>0,且a≠1)叫做对数函数(logarithmic function),其中x是自变量,定义域是(0,+∞).
注意:对数函数与指数函数的关系.
作业布置
作业:p140. 习题4.4 1,3.
补充题:
1.已知对数函数f(x)=(m2-3m+3)·logmx,则m= .
2.(多选题)下列各个函数中,是对数函数的是( )
A.y=log5x B.y=2log5 (x+3) C.y=log3|x| D.y=
3.求下列函数定义域:
⑴y=; ⑵y=log2x-1(3x2-8x+4);
⑶y=.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第4章 指数函数与对数函数
4.4 对数函数
4.4.1 对数函数的概念
人教A版(2019)
教学目标
学习目标 数学素养
1.理解对数函数的概念. 1.数学类比、数学抽象素养.
2.会求与对数函数有关的定义域问题. 2.数学运算素养
3.了解对数函数在生产实际中的简单应用. 3.数学建模素养.
温故知新
1.对数的定义
一般地, 如果ax=N(a>0, 且a≠1), 那么数x叫做以a为底N的对数, 记作 其中a叫做对数的底数, N叫做真数.
x = logaN ,
注意:0和负数没有对数;
2.对数与指数之间的关系
ax =N logaN = x
温故知新
3. 指数函数y=ax分的图象和性质
图象
定义域 值域 性质
y=ax
0
R
(0,+∞)
过定点(0, 1)
在R上单调递增
在R上单调递减
x>0 , 0
x>0 , y>1;
x<0 , 0
在4.2.1的问题2中,我们已经研究了死亡生物体内碳14的含量y随死亡时间x的变化而衰减的规律. 反过来,已知死亡生物体内碳14的含量,如何得知它死亡了多长时间呢?进一步地,死亡时间x是碳14的含量y的函数吗?
根据指数与对数的关系,
如右图,过y轴正半轴上任意一点(0,y0)(0<y0≤1)作x轴的平行线,与y=的图象有且只有一个交点(x0 , y0).
新知探究
这说明对任意一个y∈(0,1],通过对应关系在[0,+∞)上都有唯一确定的数x和它对应.
所以x也是y的函数,也就是说,函数 (y∈(0,1])刻画了时间x随碳14含量y的衰减而变化的规律.
同样地,根据指数与对数的关系,由y=ax (a>0, 且a≠1)可以得到 x=logay (a>0, 且a≠1),x也是y的函数.
通常我们用x表示自变量,y表示函数.
为此将x=logay (a>0, 且a≠1)中的字母x和y对调,写成y=logax (a>0, 且a≠1).
对数函数定义:一般地,函数y=logax(a>0,且a≠1)叫做对数函数(logarithmic function),其中x是自变量,定义域是(0,+∞).
新知探究
想一想
(1)对数函数的定义域为什么是(0,+∞)
(2)对数函数的解析式有何特征?
(1)ax=N logaN=x,真数为幂值N,而N>0,故式子logax中,x>0.
(2)①a>0,且a≠1;②logax的系数为1;③自变量x的系数为1.
注意:在对数函数y=logax中,
①a>0,且a≠1;
②x∈(0,+∞);
③必须符合对数函数的三个特征.
新知讲授
概念辨析:下列函数表达式中,是对数函数的有( )
①y=logx2; ②y=logax(a∈R); ③y=log8x; ④y=lnx;
⑤y=logx(x+2);⑥y=2log4x; ⑦y=log2(x+1).
A.1个 B.2个 C.3个 D.4个
解析:
①中自变量出现在底数上,∴①不是对数函数;
②中底数a∈R不能保证a>0且a≠1;
⑤、⑦的真数分别为(x+2),(x+1);
⑥中log4x系数为2;
只有③、④符合对数函数的定义.故选B.
B
新知讲解
【例1】求下列函数的定义域:
(1) y=log3x2; (2) y=loga(4-x) (a>0, 且a≠1);
解:
(1)∵即
∴函数的定义域是
(2)∵即
∴的定义域是
新知讲解
求对数型函数定义域的原则:
(1)分母不能为0;
(2)根指数为偶数时,被开方数非负;
(3)对数的真数大于0,底数大于0且不为1;
(4)若需对函数进行变形,则需先求出定义域,再对函数进行恒等变形.
初试身手
1.求下列函数的定义域:
解:
(2)∵,解得.
(3)∵,解得.
(1) y=ln(1-x);
⑵y=;
⑶ .
∴函数y=ln(1-x)的定义域是
(1)∵1-x>0 , 即x<1,
∴函数y=的定义域是
∴函数的定义域是
新知讲解
【例2】假设某地初始物价为1, 每年以5%的增长率递增,经过y年后的物价为x.
(1)该地的物价经过几年后会翻一番?
(2)填写下表,并根据表中的数据, 说明该地物价的变化规律.
解:
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
(1)由题意可知,经过y年后物价x为
x=(1+5%)y ,
即x=1.05y (y∈[0,+∞))
由对数与指数间的关系,可得
y=log1.05x (x∈[1, +∞)).
由计算工具可得,当x=2时,y≈14.
所以,该地区的物价大约经过14年后会翻一番.
新知讲解
【例2】假设某地初始物价为1, 每年以5%的增长率递增,经过y年后的物价为x.
(1)该地的物价经过几年后会翻一番?
(2)填写下表,并根据表中的数据, 说明该地物价的变化规律.
解:
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
(2)根据函数y=log1.05x (x∈[1, +∞)),利用计算工具,可得
数据表明该地区的物价随时间增长而增长,但大约每增加1倍所需要的时间在逐渐缩小.
14
23
28
33
37
40
43
45
47
初试身手
解析:当时,,当λ时,,
∴=1+0.6,∴λ=1579.故选C.
2.我国的5G通信技术领先世界,5G技术的数学原理之一是著名的香农(Shannon)公式,香农提出并严格证明了“在被高斯白噪声干扰的信道中,计算最大信息传送速率C的公式 C= ,其中W是信道带宽(赫兹),S是信道内所传信号的平均功率(瓦),N是信道内部的高斯噪声功率(瓦),其中叫做信噪比.根据此公式,在不改变W的前提下,将信噪比从99提升至λ,使得C大约增加了60%,则λ的值大约为( ) (参考数据:100.2≈1.58)
A.1 559 B.3 943 C.1 579 D.2 512
C
拓展延申
求下列函数的定义域:
⑴f(x)= ; ⑵f(x)=;
⑶f(x)=.
解:
解得x>0且x≠1,
所以此函数的定义域为{x|x>0且x≠1}.
⑴要使函数有意义,必有,
⑵要使函数有意义,必有(3-x)(3+x)>0,
解得-3
⑶要使函数有意义,必有,
解得0
课堂小结
2.求与对数函数有关的函数的定义域.
3.对数函数模型问题的求解.
1.对数函数定义:一般地,函数y=logax(a>0,且a≠1)叫做对数函数(logarithmic function),其中x是自变量,定义域是(0,+∞).
注意:对数函数与指数函数的关系.
作业布置
作业:p140. 习题4.4 1,3.
补充题:
1.已知对数函数f(x)=(m2-3m+3)·logmx,则m= .
2.(多选题)下列各个函数中,是对数函数的是( )
A.y=log5x B.y=2log5 (x+3) C.y=log3|x| D.y=
3.求下列函数定义域:
⑴y=; ⑵y=log2x-1(3x2-8x+4);
⑶y=.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
