4.4.3&4.5.3不同函数增长的差异与函数模型的应用 学案
文档属性
| 名称 | 4.4.3&4.5.3不同函数增长的差异与函数模型的应用 学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 21:40:57 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.4.3&4.5.3不同函数增长的差异与函数模型的应用
班级 姓名
学习目标
1.了解常用的描述现实世界中不同增长规律的函数模型.
2.会分析具体的实际问题,通过建模解决实际问题.
3.了解拟合函数模型并解决实际问题.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 知识点 三种函数模型的增长差异y=ax(a>1)y=logax(a>1)y=kx(k>0)在(0,+∞)上的增减性 图象的变化趋势随x增大逐渐近似与 平行随x增大逐渐近似与 平行保持固定增长速度增长速度y=ax(a>1):随着x的增大,y增长速度 ,会远远大于y=kx(k>0)的增长速度,y=logax(a>1)的增长速度 增长结果存在一个x0,当x>x0时,有 【即时训练1】(1)下列函数中,增长速度最快的是( )A. B.C. D.y=2023x(2)下面对函数,与在区间(0,+∞)上的递减情况说法正确的是( )A.f(x)递减速度越来越慢,g(x)递减速度越来越快,h(x)递减速度越来越慢B.f(x)递减速度越来越快,g(x)递减速度越来越慢,h(x)递减速度越来越快C.f(x)递减速度越来越慢,g(x)递减速度越来越慢,h(x)递减速度不变D.f(x)递减速度越来越快,g(x)递减速度越来越快,h(x)递减速度越来越快
阅读教材,完成右边的内容 知识点 常见函数模型(1)一次函数模型y=kx+b(k,b为常数,k≠0)(2)二次函数模型y=ax2+bx+c(a,b,c为常数,a≠0)(3)指数函数模型y=bax+c(a,b,c为常数,b≠0,a>0且a≠1)(4)对数函数模型y=mlogax+n(m,a,n为常数,m≠0,a>0且a≠1)(5)幂函数模型y=axn+b(a,b为常数,a≠0)(6)分段函数模型y=【即时训练2】有一组实验数据如下表所示:t1.993.04.05.16.12u1.54.047.51218.01则能体现这些数据关系的函数模型是( )A.u=log2t B.u=2t-2 C.u= D.u=2t-2
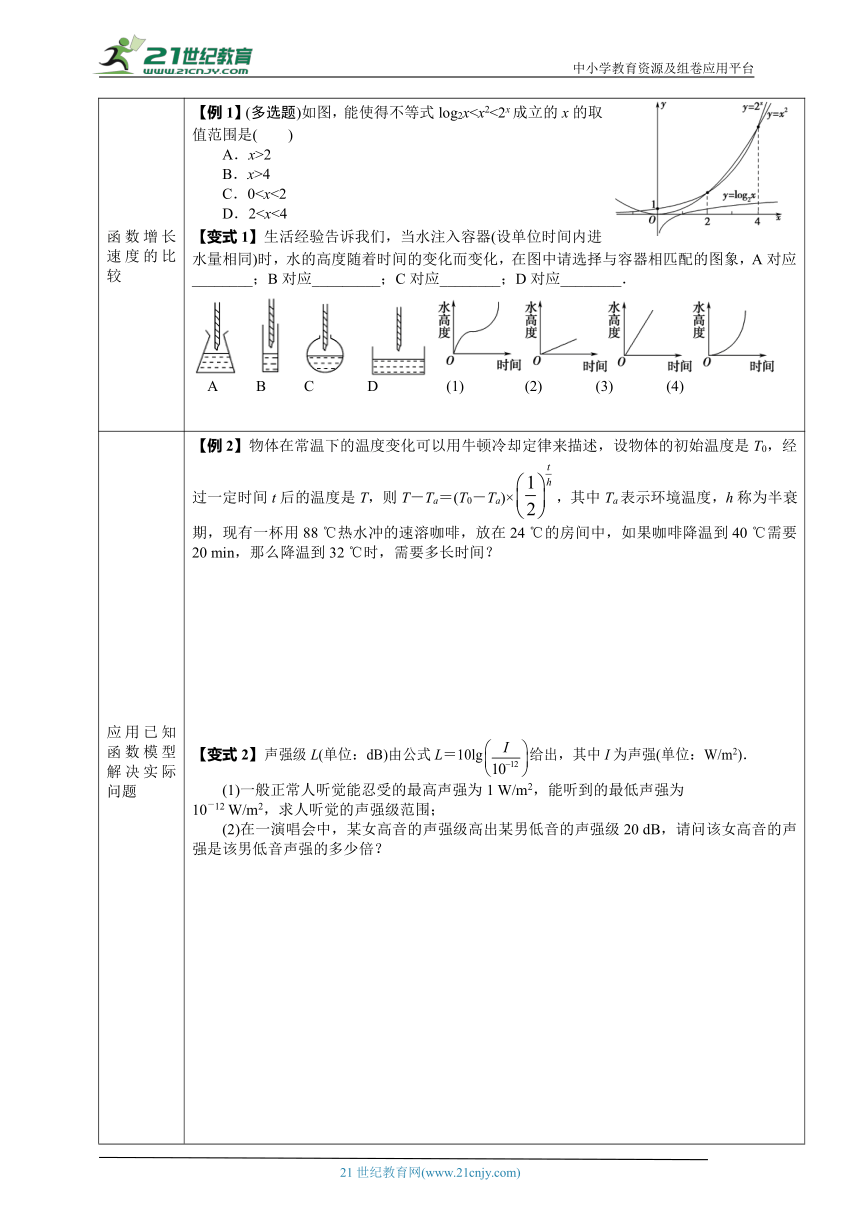
函数增长速度的比较 【例1】(多选题)如图,能使得不等式log2x2B.x>4C.0应用已知函数模型解决实际问题 【例2】物体在常温下的温度变化可以用牛顿冷却定律来描述,设物体的初始温度是T0,经过一定时间t后的温度是T,则T-Ta=(T0-Ta)×,其中Ta表示环境温度,h称为半衰期,现有一杯用88 ℃热水冲的速溶咖啡,放在24 ℃的房间中,如果咖啡降温到40 ℃需要20 min,那么降温到32 ℃时,需要多长时间?【变式2】声强级L(单位:dB)由公式L=10lg给出,其中I为声强(单位:W/m2).(1)一般正常人听觉能忍受的最高声强为1 W/m2,能听到的最低声强为10-12 W/m2,求人听觉的声强级范围;(2)在一演唱会中,某女高音的声强级高出某男低音的声强级20 dB,请问该女高音的声强是该男低音声强的多少倍?
课后作业
一、基础训练题
1.(多选题)下面是一幅统计图,根据此图得到的以下说法中正确的是( )
A.这几年生活水平逐年得到提高
B.生活费收入指数增长最快的一年是2016年
C.生活价格指数上涨速度最快的一年是2017年
D.虽然2018年生活费收入增长缓慢,但生活价格指数也略有降低,因而生活水平有较大的改善
2.三个变量y1,y2,y3随着变量x的变化情况如下表:
x 1 3 5 7 9 11
y1 5 135 625 1715 3645 6655
y2 5 29 245 2189 19685 177149
y3 5 6.10 6.61 6.985 7.2 7.4
则关于x分别呈对数函数、指数函数、幂函数变化的变量依次为( )
A.y1,y2,y3 B.y2,y1,y3 C.y3,y2,y1 D.y1,y3,y2
3.某地区植被被破坏,土地沙漠化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y公顷关于年数x的函数关系较为近似的是( )
A.y=0.2x B.y=(x2+2x) C.y= D.y=0.2+log16x
4.如图所示,点P在边长为1的正方形的边上运动,M是CD的中点.当点P沿路线A-B-C-M运动时,点P经过的路程x与△APM的面积y之间的函数y=f(x)的图象大致是( )
5.麋鹿是国家一级保护动 ( http: / / www.21cnjy.com )物,位于江苏省中部黄海之滨的江苏大丰麋鹿国家级自然保护区,成立于1985年,最初一年年底只有麋鹿100头,由于科学的人工培育,这种当初快要濒临灭绝的动物的数量y(头)与时间x(年)的关系可以近似地由关系式y=alog2(x+1)给出,则2000年年底它们的数量约为________头.
6.已知某工厂生产某种产品的月产量y与月份x满足关系y=a·0.5x+b,现已知该厂今年1月、2月生产该产品分别为1万件、1.5万件.则此厂3月份该产品的产量为________万件.
7.某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费;超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元,则此次出租车行驶了________km.
8.大西洋鲑鱼每年都要逆流而上,游回产地产卵.记鲑鱼的游速为V(m/s),鲑鱼的耗氧量的单位数为Q,研究中发现V与log3成正比,且当Q=900时,V=1.
(1)求出V关于Q的函数解析式;
(2)计算一条鲑鱼的游速是1.5 m/s时耗氧量的单位数.
9.为了预防流感,某学校对教室用过氧乙酸熏蒸进行消毒.已知药物在释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比,药物释放完毕后,y与t的函数关系式为y=(a为常数),如图所示.
(1)从药物释放开始,写出y与t的函数关系式;
(2)据测定,当教室空气中的含药量降低到每立方米0.25毫克以下时,学生可进教室,问这次消毒多久后学生才能回到教室.
二、综合训练题
10.衣柜里的樟脑丸,随着时间会挥发而体积缩小,刚放进去的新丸体积为a,经过t天后体积V与天数t的关系式为:.已知新丸经过50天后,体积变为.若一个新丸体积变为,则需经过的天数为( )
A.125 B.100 C.75 D.50
11.用清水洗衣服,若每次能洗去污垢的,要使存留的污垢不超过1%,则至少要清洗的次数是________(lg 2≈0.301 0).
三、能力提升题
12.一片森林原来的面积为a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的,已知到今年为止,森林剩余面积为原来的.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
4.4.3 不同函数增长的差异
参考答案
1、[答案] ABD
[解析] 由题意知,“生活费收入指数”减去“生活价格指数”的差是逐年增大的,故A正确;“生活费收入指数”在2016~2017年最陡,故B正确;“生活价格指数”在2017~2018年最平缓,故C不正确;“生活价格指数”略呈下降,而“生活费收入指数”呈上升趋势,故D正确.
2、[答案] C
[解析] 通过指数函数、对数函数、幂函数等 ( http: / / www.21cnjy.com )不同函数模型的增长规律比较可知,对数函数的增长速度越来越慢,变量y3随x的变化符合此规律;指数函数的增长速度越来越快,y2随x的变化符合此规律;幂函数的增长速度介于指数函数与对数函数之间,y1随x的变化符合此规律,故选C.
3、[答案] C
[解析]用排除法,当x=1时,排除B项;当x=2时,排除D项;当x=3时,排除A项.
[答案] A
[解析]由题意得,当0当1=××1-×1×(x-1)-××(2-x)=-x+;
当25、[答案] 400
[解析] 由题意,x=1时y=100,代入求得a=100,2000年年底时,x=15,代入得y=400.
6、[答案] 1.75
[解析]∵y=a·0.5x+b,且当x=1时,y=1,当x=2时,y=1.5,
则有解得∴y=-2×0.5x+2.
当x=3时,y=-2×0.125+2=1.75(万件).
7、[答案] 9
[解析] [设出租车行驶x km时,付费y元,
则y=由y=22.6,解得x=9.
8、[解析] (1)设V=k·log3,∵当Q=900时,V=1,∴1=k·log3,
∴k=,∴V关于Q的函数解析式为V=log3.
(2)令V=1.5,则1.5=log3,
∴Q=2700,即一条鲑鱼的游速是1.5 m/s时耗氧量为2700个单位.
9、[解析] (1)由图象可知,当0≤t≤0.1时,y=10t;当t=0.1时,由1=,得a=0.1,
∴当t>0.1时,y=.∴y=
(2)由题意可知,<0.25,解得t>0.6,即这次消毒0.6×60=36(分钟)后,学生才能进教室.
10、[答案] C
[解析]由已知,得a=a·e-50k,∴e-k=.
设经过t1天后,一个新丸体积变为a,则a=a·e-kt1,
∴=(e-k)t1=,∴=,t1=75.
11、[答案] 4
[解析]设至少要洗x次,则≤,所以x≥≈3.322,所以需4次.
12、[解析] (1)设每年砍伐面积的百分比为x(0则a(1-x)10=a,即(1-x)10=,解得x=1-.
(2)设经过m年后森林剩余面积为原来的,则a(1-x)m=a,
即=,则=,解得m=5.故到今年为止,该森林已砍伐了5年.
(3)设从今年开始,以后砍了n年,则n年后剩余面积为a(1-x)n.
令a(1-x)n≥a,即(1-x)n≥,则≥,则≤,解得n≤15.
故今后最多还能砍伐15年.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
4.4.3&4.5.3不同函数增长的差异与函数模型的应用
班级 姓名
学习目标
1.了解常用的描述现实世界中不同增长规律的函数模型.
2.会分析具体的实际问题,通过建模解决实际问题.
3.了解拟合函数模型并解决实际问题.
学习过程
自学指导 自学检测及课堂展示
阅读教材,完成右边的内容 知识点 三种函数模型的增长差异y=ax(a>1)y=logax(a>1)y=kx(k>0)在(0,+∞)上的增减性 图象的变化趋势随x增大逐渐近似与 平行随x增大逐渐近似与 平行保持固定增长速度增长速度y=ax(a>1):随着x的增大,y增长速度 ,会远远大于y=kx(k>0)的增长速度,y=logax(a>1)的增长速度 增长结果存在一个x0,当x>x0时,有 【即时训练1】(1)下列函数中,增长速度最快的是( )A. B.C. D.y=2023x(2)下面对函数,与在区间(0,+∞)上的递减情况说法正确的是( )A.f(x)递减速度越来越慢,g(x)递减速度越来越快,h(x)递减速度越来越慢B.f(x)递减速度越来越快,g(x)递减速度越来越慢,h(x)递减速度越来越快C.f(x)递减速度越来越慢,g(x)递减速度越来越慢,h(x)递减速度不变D.f(x)递减速度越来越快,g(x)递减速度越来越快,h(x)递减速度越来越快
阅读教材,完成右边的内容 知识点 常见函数模型(1)一次函数模型y=kx+b(k,b为常数,k≠0)(2)二次函数模型y=ax2+bx+c(a,b,c为常数,a≠0)(3)指数函数模型y=bax+c(a,b,c为常数,b≠0,a>0且a≠1)(4)对数函数模型y=mlogax+n(m,a,n为常数,m≠0,a>0且a≠1)(5)幂函数模型y=axn+b(a,b为常数,a≠0)(6)分段函数模型y=【即时训练2】有一组实验数据如下表所示:t1.993.04.05.16.12u1.54.047.51218.01则能体现这些数据关系的函数模型是( )A.u=log2t B.u=2t-2 C.u= D.u=2t-2
函数增长速度的比较 【例1】(多选题)如图,能使得不等式log2x
课后作业
一、基础训练题
1.(多选题)下面是一幅统计图,根据此图得到的以下说法中正确的是( )
A.这几年生活水平逐年得到提高
B.生活费收入指数增长最快的一年是2016年
C.生活价格指数上涨速度最快的一年是2017年
D.虽然2018年生活费收入增长缓慢,但生活价格指数也略有降低,因而生活水平有较大的改善
2.三个变量y1,y2,y3随着变量x的变化情况如下表:
x 1 3 5 7 9 11
y1 5 135 625 1715 3645 6655
y2 5 29 245 2189 19685 177149
y3 5 6.10 6.61 6.985 7.2 7.4
则关于x分别呈对数函数、指数函数、幂函数变化的变量依次为( )
A.y1,y2,y3 B.y2,y1,y3 C.y3,y2,y1 D.y1,y3,y2
3.某地区植被被破坏,土地沙漠化越来越严重,最近三年测得沙漠增加值分别为0.2万公顷、0.4万公顷和0.76万公顷,则沙漠增加数y公顷关于年数x的函数关系较为近似的是( )
A.y=0.2x B.y=(x2+2x) C.y= D.y=0.2+log16x
4.如图所示,点P在边长为1的正方形的边上运动,M是CD的中点.当点P沿路线A-B-C-M运动时,点P经过的路程x与△APM的面积y之间的函数y=f(x)的图象大致是( )
5.麋鹿是国家一级保护动 ( http: / / www.21cnjy.com )物,位于江苏省中部黄海之滨的江苏大丰麋鹿国家级自然保护区,成立于1985年,最初一年年底只有麋鹿100头,由于科学的人工培育,这种当初快要濒临灭绝的动物的数量y(头)与时间x(年)的关系可以近似地由关系式y=alog2(x+1)给出,则2000年年底它们的数量约为________头.
6.已知某工厂生产某种产品的月产量y与月份x满足关系y=a·0.5x+b,现已知该厂今年1月、2月生产该产品分别为1万件、1.5万件.则此厂3月份该产品的产量为________万件.
7.某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费;超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元,则此次出租车行驶了________km.
8.大西洋鲑鱼每年都要逆流而上,游回产地产卵.记鲑鱼的游速为V(m/s),鲑鱼的耗氧量的单位数为Q,研究中发现V与log3成正比,且当Q=900时,V=1.
(1)求出V关于Q的函数解析式;
(2)计算一条鲑鱼的游速是1.5 m/s时耗氧量的单位数.
9.为了预防流感,某学校对教室用过氧乙酸熏蒸进行消毒.已知药物在释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比,药物释放完毕后,y与t的函数关系式为y=(a为常数),如图所示.
(1)从药物释放开始,写出y与t的函数关系式;
(2)据测定,当教室空气中的含药量降低到每立方米0.25毫克以下时,学生可进教室,问这次消毒多久后学生才能回到教室.
二、综合训练题
10.衣柜里的樟脑丸,随着时间会挥发而体积缩小,刚放进去的新丸体积为a,经过t天后体积V与天数t的关系式为:.已知新丸经过50天后,体积变为.若一个新丸体积变为,则需经过的天数为( )
A.125 B.100 C.75 D.50
11.用清水洗衣服,若每次能洗去污垢的,要使存留的污垢不超过1%,则至少要清洗的次数是________(lg 2≈0.301 0).
三、能力提升题
12.一片森林原来的面积为a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的,已知到今年为止,森林剩余面积为原来的.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
4.4.3 不同函数增长的差异
参考答案
1、[答案] ABD
[解析] 由题意知,“生活费收入指数”减去“生活价格指数”的差是逐年增大的,故A正确;“生活费收入指数”在2016~2017年最陡,故B正确;“生活价格指数”在2017~2018年最平缓,故C不正确;“生活价格指数”略呈下降,而“生活费收入指数”呈上升趋势,故D正确.
2、[答案] C
[解析] 通过指数函数、对数函数、幂函数等 ( http: / / www.21cnjy.com )不同函数模型的增长规律比较可知,对数函数的增长速度越来越慢,变量y3随x的变化符合此规律;指数函数的增长速度越来越快,y2随x的变化符合此规律;幂函数的增长速度介于指数函数与对数函数之间,y1随x的变化符合此规律,故选C.
3、[答案] C
[解析]用排除法,当x=1时,排除B项;当x=2时,排除D项;当x=3时,排除A项.
[答案] A
[解析]由题意得,当0
当2
[解析] 由题意,x=1时y=100,代入求得a=100,2000年年底时,x=15,代入得y=400.
6、[答案] 1.75
[解析]∵y=a·0.5x+b,且当x=1时,y=1,当x=2时,y=1.5,
则有解得∴y=-2×0.5x+2.
当x=3时,y=-2×0.125+2=1.75(万件).
7、[答案] 9
[解析] [设出租车行驶x km时,付费y元,
则y=由y=22.6,解得x=9.
8、[解析] (1)设V=k·log3,∵当Q=900时,V=1,∴1=k·log3,
∴k=,∴V关于Q的函数解析式为V=log3.
(2)令V=1.5,则1.5=log3,
∴Q=2700,即一条鲑鱼的游速是1.5 m/s时耗氧量为2700个单位.
9、[解析] (1)由图象可知,当0≤t≤0.1时,y=10t;当t=0.1时,由1=,得a=0.1,
∴当t>0.1时,y=.∴y=
(2)由题意可知,<0.25,解得t>0.6,即这次消毒0.6×60=36(分钟)后,学生才能进教室.
10、[答案] C
[解析]由已知,得a=a·e-50k,∴e-k=.
设经过t1天后,一个新丸体积变为a,则a=a·e-kt1,
∴=(e-k)t1=,∴=,t1=75.
11、[答案] 4
[解析]设至少要洗x次,则≤,所以x≥≈3.322,所以需4次.
12、[解析] (1)设每年砍伐面积的百分比为x(0
(2)设经过m年后森林剩余面积为原来的,则a(1-x)m=a,
即=,则=,解得m=5.故到今年为止,该森林已砍伐了5年.
(3)设从今年开始,以后砍了n年,则n年后剩余面积为a(1-x)n.
令a(1-x)n≥a,即(1-x)n≥,则≥,则≤,解得n≤15.
故今后最多还能砍伐15年.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
