12.3平行线的性质 课件 2023-2024学年人教版(五四制)数学七年级上册
文档属性
| 名称 | 12.3平行线的性质 课件 2023-2024学年人教版(五四制)数学七年级上册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 09:13:32 | ||
图片预览





文档简介
(共18张PPT)
12.3平行线的性质
平行线的判定方法
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行;
(4)两条直线都垂直于同一条直线,那么这两条直线平行.
复习回顾
根据同位角相等可以判定两直线平行,反过来如果两直线平行,同位角之间有什么关系呢?
内错角、同旁内角之间又有什么关系呢?
发现问题
画两条平行线a//b,然后画一条截线c与a、b相交. 度量所形成的8个角的度数,把结果填入下表.
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
110°
70°
110°
70°
110°
70°
110°
70°
发现:∠1 ∠5, ∠2 ∠6, ∠3 ∠7, ∠4 ∠8。
=
=
=
=
探究新知
两直线平行,同位角相等.
平行线的性质1:
两条平行线被第三条直线所截,同位角相等.
∴∠1=∠2.(两直线平行,同位角相等)
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
得出性质
合作交流
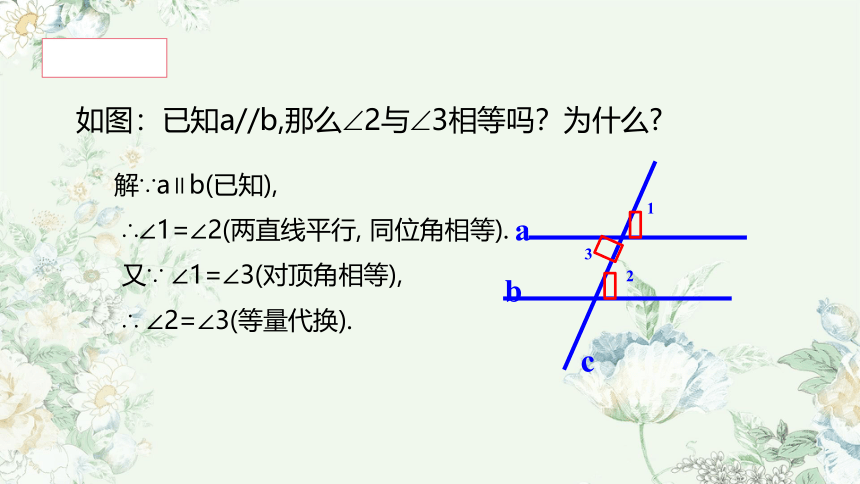
如图:已知a//b,那么 2与 3相等吗?为什么
解∵a∥b(已知),
∴∠1=∠2(两直线平行, 同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
得出性质
b
1
2
a
c
3
两直线平行,内错角相等.
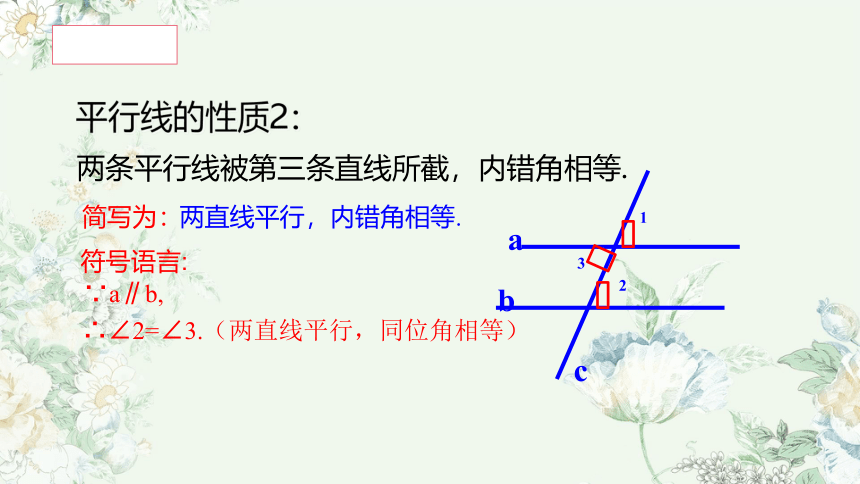
平行线的性质2:
两条平行线被第三条直线所截,内错角相等.
简写为:
∴∠2=∠3.(两直线平行,同位角相等)
∵a∥b,
符号语言:
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
∴ 1= 2(两直线平行,同位角相等).
∵ 1+ 4=180°(邻补角定义),
∴ 2+ 4=180°(等量代换).
合作交流
得出性质
两直线平行,同旁内角互补.
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补.
简写为:
∴∠2+∠4=180°.(两直线平行,同位角相等)
∵a∥b,
符号语言:
b
1
2
a
c
4
合作释疑
如图,已知直线a∥b,∠1 = 500,求∠2的度数.
∴∠ 2= 500 (等量代换).
解:∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 500 (已知),
变式1:已知条件不变,求∠3,∠4的度数?
a
b
c
1
2
3
4
平行线的性质:
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补;
整理归纳
当堂检测
如图,在四边形ABCD中,已知AD∥BC,∠D=60°,求∠B的度数。不用度量的方法 能否求得∠A的度数?
解:∵AD∥BC(已知)
∴∠A+∠B=180° (两直线平行,同旁内角互补)
又∵ ∠A=60° (已知)
∴ ∠B=120°
根据题目的已知条件,无法求出∠D的度数。
你能添加一个条件,求出∠D的度数吗
(2)判定是根据两角相等或互补,证明两条直线 平行.
平行线的性质与判定的区别与联系
1、区别:
2、联系
(1)它们都以两条直线被第三条直线所截为前提;
(2)它们的条件和结论是互逆的.
(1)性质是根据两条直线平行,去证角的相等或互补.
例题与练习
练习
1. 如图,直线 a∥b,∠1 = 54°,∠2,∠3,∠4 各是多少度?
解:∵a∥b,∠1=54°,∴∠4 =∠1 = 54°(两直线平行,同位角相等).
∠3 =180°-∠4
=180° - 54°=126°,
∠2 与∠1 是对顶角,
∴∠2=∠1= 54°.
如图,若∠1+∠2=180°,∠3=110°,则∠4=_______.
110°
(人教7下P23改编)如图,已知AB∥CD.
(1)若∠B=130°,∠D=152°,求∠BED的度数;
(2)请猜想∠B+∠E+∠D的度数,并说明理由.
【例4】(创新题)(北师8上P186改编)如图,AB∥CD,点E在直线AB上,点F在直线CD上,直线EO,FO相交于直线AB,CD之间的一点O.
(1)借助三角尺过点O画直线MN,使MN∥CD;
(2)直线MN与AB平行吗 为什么
(3)试判断∠BEO,∠DFO,∠EOF之间的关系,并说明理由.
再见
12.3平行线的性质
平行线的判定方法
(1)同位角相等,两直线平行;
(2)内错角相等,两直线平行;
(3)同旁内角互补,两直线平行;
(4)两条直线都垂直于同一条直线,那么这两条直线平行.
复习回顾
根据同位角相等可以判定两直线平行,反过来如果两直线平行,同位角之间有什么关系呢?
内错角、同旁内角之间又有什么关系呢?
发现问题
画两条平行线a//b,然后画一条截线c与a、b相交. 度量所形成的8个角的度数,把结果填入下表.
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
110°
70°
110°
70°
110°
70°
110°
70°
发现:∠1 ∠5, ∠2 ∠6, ∠3 ∠7, ∠4 ∠8。
=
=
=
=
探究新知
两直线平行,同位角相等.
平行线的性质1:
两条平行线被第三条直线所截,同位角相等.
∴∠1=∠2.(两直线平行,同位角相等)
∵a∥b,
简写为:
符号语言:
b
1
2
a
c
得出性质
合作交流
如图:已知a//b,那么 2与 3相等吗?为什么
解∵a∥b(已知),
∴∠1=∠2(两直线平行, 同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
得出性质
b
1
2
a
c
3
两直线平行,内错角相等.
平行线的性质2:
两条平行线被第三条直线所截,内错角相等.
简写为:
∴∠2=∠3.(两直线平行,同位角相等)
∵a∥b,
符号语言:
解: ∵a//b (已知),
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
∴ 1= 2(两直线平行,同位角相等).
∵ 1+ 4=180°(邻补角定义),
∴ 2+ 4=180°(等量代换).
合作交流
得出性质
两直线平行,同旁内角互补.
平行线的性质3:
两条平行线被第三条直线所截,同旁内角互补.
简写为:
∴∠2+∠4=180°.(两直线平行,同位角相等)
∵a∥b,
符号语言:
b
1
2
a
c
4
合作释疑
如图,已知直线a∥b,∠1 = 500,求∠2的度数.
∴∠ 2= 500 (等量代换).
解:∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 500 (已知),
变式1:已知条件不变,求∠3,∠4的度数?
a
b
c
1
2
3
4
平行线的性质:
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补;
整理归纳
当堂检测
如图,在四边形ABCD中,已知AD∥BC,∠D=60°,求∠B的度数。不用度量的方法 能否求得∠A的度数?
解:∵AD∥BC(已知)
∴∠A+∠B=180° (两直线平行,同旁内角互补)
又∵ ∠A=60° (已知)
∴ ∠B=120°
根据题目的已知条件,无法求出∠D的度数。
你能添加一个条件,求出∠D的度数吗
(2)判定是根据两角相等或互补,证明两条直线 平行.
平行线的性质与判定的区别与联系
1、区别:
2、联系
(1)它们都以两条直线被第三条直线所截为前提;
(2)它们的条件和结论是互逆的.
(1)性质是根据两条直线平行,去证角的相等或互补.
例题与练习
练习
1. 如图,直线 a∥b,∠1 = 54°,∠2,∠3,∠4 各是多少度?
解:∵a∥b,∠1=54°,∴∠4 =∠1 = 54°(两直线平行,同位角相等).
∠3 =180°-∠4
=180° - 54°=126°,
∠2 与∠1 是对顶角,
∴∠2=∠1= 54°.
如图,若∠1+∠2=180°,∠3=110°,则∠4=_______.
110°
(人教7下P23改编)如图,已知AB∥CD.
(1)若∠B=130°,∠D=152°,求∠BED的度数;
(2)请猜想∠B+∠E+∠D的度数,并说明理由.
【例4】(创新题)(北师8上P186改编)如图,AB∥CD,点E在直线AB上,点F在直线CD上,直线EO,FO相交于直线AB,CD之间的一点O.
(1)借助三角尺过点O画直线MN,使MN∥CD;
(2)直线MN与AB平行吗 为什么
(3)试判断∠BEO,∠DFO,∠EOF之间的关系,并说明理由.
再见
