24.2 直角三角形的性质(第1课时)课件 2023--2024学年华东师大版九年级数学上册
文档属性
| 名称 | 24.2 直角三角形的性质(第1课时)课件 2023--2024学年华东师大版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 348.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 09:09:15 | ||
图片预览





文档简介
(共19张PPT)
24.2直角三角形的性质
第 24章 解直角三角形
学习目标
1
2
掌握“直角三角形斜边上的中线等于斜边的一半”
和”含30 °的直角三角形”的性质. (重点)
会运用直角三角形的性质解决有关问题.(难点)
3
掌握直角三角形边、角的性质.(重点)
知识回顾
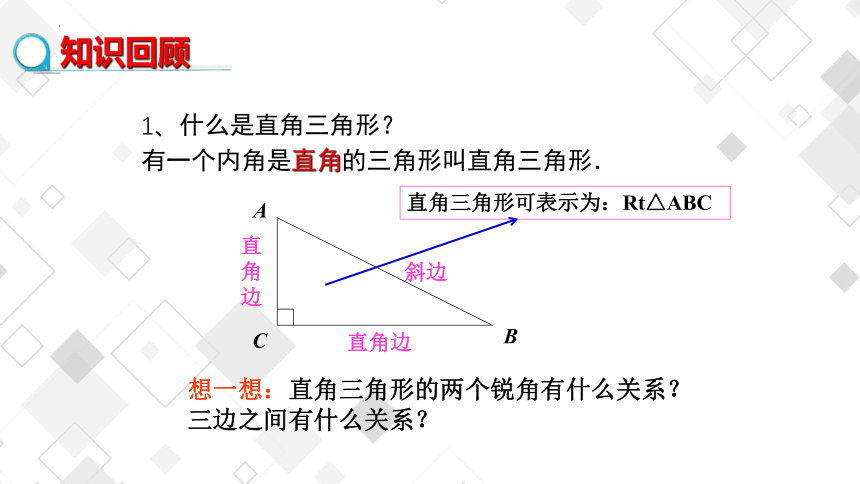
1、什么是直角三角形?
有一个内角是直角的三角形叫直角三角形.
直角三角形可表示为:Rt△ABC
A
C
B
斜边
直角边
直角边
想一想:直角三角形的两个锐角有什么关系?三边之间有什么关系?
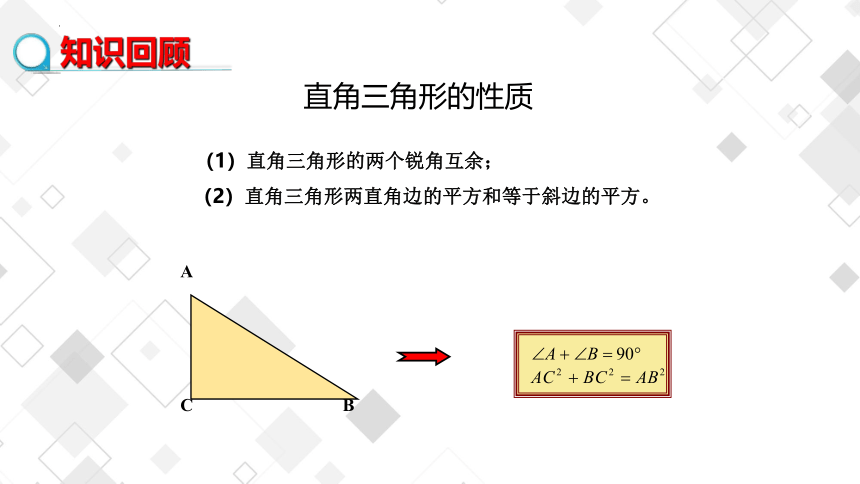
(1)直角三角形的两个锐角互余;
A
B
C
(2)直角三角形两直角边的平方和等于斜边的平方。
直角三角形的性质
知识回顾
如图,画Rt△ABC,并画出斜边AB上的中线CD。
(1)量一量,看看CD与AB有什么关系?
(2)你能用演绎推理证明这个猜想吗?
B
A
C
D
【发现】CD恰好是AB的一半,即直角三角形斜边上的中
线等于斜边的一半。
知识讲解
直 角 三 角 形 的 性 质
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线。
求证:
D
B
A
C
E
知识讲解
证明:
延长CD到点E,使DE=CD,连结AE、BE.
∵ CD是斜边AB的中线,
∴ AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90 ° ,
∴ 四边形ACBE是矩形,
∴ CE=AB.
∴
探究发现
★ 在直角三角形中,斜边上的中线等于斜边的一半.
D
B
A
C
1.已知Rt△ABC中,斜边AB=10cm,则斜边上的中线的长为______.
2.如图,在Rt△ABC中,CD是斜边AB上的中线∠CDA=80°,则∠A=_____ ,∠B=_____.
5cm
50°
40°
练一练
如图,画Rt△ABC,使得∠ACB=90°,∠A=30°.
(1)量一量,看看BC与AB有什么关系?
(2)你能用演绎推理证明这个猜想吗?
【发现】在直角三角形中,如果一个锐角等于30°,那么
它所对的直角边等于斜边的一半。
B
A
C
30°
知识讲解
直 角 三 角 形 的 性 质
如图,在Rt△ABC中,∠ACB=90°,∠A=30°.
求证:
B
A
C
30°
D
△DBC是等边三角形
BC=BD
知识讲解
探究发现
★在直角三角形中,30°角所对的直角边等于斜边的一半.
D
B
A
C
3.如图,在△ABC中,若∠BAC=120°,AB=AC, AD⊥AC于点A,BD=3,则BC=______.
9
练一练
A
B
C
D
(1)直角三角形的两个锐角互余;
(2)直角三角形两直角边的平方和等于斜边的平方。
(3)直角三角形斜边上的中线等于斜边的一半。
A
B
C
D
(4)直角三角形中30度的锐角所对的直角边等于斜边的一半。
总结归纳
直 角 三 角 形 的 性 质
如图,点O是矩形ABCD的对角线AC的中点,M是AD的中点,且
(1)求BO的长;
(2)求四边形ABOM的周长。
AB=5,AD=12.
O
A
B
C
D
M
【规律】(1)在直角三角形中,出现斜边上的中线,求线段的长,常用此性质;(2)本题综合考查了矩形的性质、直角三角形斜边上的中线的性质、三角形中
位线的性质,熟记性质并准确识图是解题的关键。
学以致用
例1
学以致用
如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN交
AC于点D.求证:CD=2BD.
A
B
C
M
N
D
例2
学以致用
如图,在△ABC中,∠ACB=90°,∠B=30°,CE垂直于AB于点E,D是AB的中点.
(1)求证:AE=ED;
(2)若AC=2,求BC的长.
例3
学以致用
拓展.如图,在△ABC中,BD、CE是高,M、N分别是BC、ED的中点,试说明:MN⊥DE.
解:连结EM、DM.
∵BD、CE是高,M是BC中点,
∴在Rt△BCE和Rt△BCD中,
∴EM=DM.
又∵N是ED中点,
∴MN⊥ED
N
M
D
E
B
C
A
,
,
BC
2
1
DM
BC
2
1
EM
=
=
性质1
直角三角形两个锐角互余
性质2
直角三角形两直角边的平方和等于斜边的平方(勾股定理)
性质3
直角三角形斜边上的中线等于斜边的一半
性质4
直角三角形中30 °角所对的直角边等于斜边的一半
课堂小结
直角三角形的性质
24.2直角三角形的性质
第 24章 解直角三角形
学习目标
1
2
掌握“直角三角形斜边上的中线等于斜边的一半”
和”含30 °的直角三角形”的性质. (重点)
会运用直角三角形的性质解决有关问题.(难点)
3
掌握直角三角形边、角的性质.(重点)
知识回顾
1、什么是直角三角形?
有一个内角是直角的三角形叫直角三角形.
直角三角形可表示为:Rt△ABC
A
C
B
斜边
直角边
直角边
想一想:直角三角形的两个锐角有什么关系?三边之间有什么关系?
(1)直角三角形的两个锐角互余;
A
B
C
(2)直角三角形两直角边的平方和等于斜边的平方。
直角三角形的性质
知识回顾
如图,画Rt△ABC,并画出斜边AB上的中线CD。
(1)量一量,看看CD与AB有什么关系?
(2)你能用演绎推理证明这个猜想吗?
B
A
C
D
【发现】CD恰好是AB的一半,即直角三角形斜边上的中
线等于斜边的一半。
知识讲解
直 角 三 角 形 的 性 质
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线。
求证:
D
B
A
C
E
知识讲解
证明:
延长CD到点E,使DE=CD,连结AE、BE.
∵ CD是斜边AB的中线,
∴ AD=BD.
又∵ DE=CD,
∴ 四边形ACBE是平行四边形.
又∵∠ACB=90 ° ,
∴ 四边形ACBE是矩形,
∴ CE=AB.
∴
探究发现
★ 在直角三角形中,斜边上的中线等于斜边的一半.
D
B
A
C
1.已知Rt△ABC中,斜边AB=10cm,则斜边上的中线的长为______.
2.如图,在Rt△ABC中,CD是斜边AB上的中线∠CDA=80°,则∠A=_____ ,∠B=_____.
5cm
50°
40°
练一练
如图,画Rt△ABC,使得∠ACB=90°,∠A=30°.
(1)量一量,看看BC与AB有什么关系?
(2)你能用演绎推理证明这个猜想吗?
【发现】在直角三角形中,如果一个锐角等于30°,那么
它所对的直角边等于斜边的一半。
B
A
C
30°
知识讲解
直 角 三 角 形 的 性 质
如图,在Rt△ABC中,∠ACB=90°,∠A=30°.
求证:
B
A
C
30°
D
△DBC是等边三角形
BC=BD
知识讲解
探究发现
★在直角三角形中,30°角所对的直角边等于斜边的一半.
D
B
A
C
3.如图,在△ABC中,若∠BAC=120°,AB=AC, AD⊥AC于点A,BD=3,则BC=______.
9
练一练
A
B
C
D
(1)直角三角形的两个锐角互余;
(2)直角三角形两直角边的平方和等于斜边的平方。
(3)直角三角形斜边上的中线等于斜边的一半。
A
B
C
D
(4)直角三角形中30度的锐角所对的直角边等于斜边的一半。
总结归纳
直 角 三 角 形 的 性 质
如图,点O是矩形ABCD的对角线AC的中点,M是AD的中点,且
(1)求BO的长;
(2)求四边形ABOM的周长。
AB=5,AD=12.
O
A
B
C
D
M
【规律】(1)在直角三角形中,出现斜边上的中线,求线段的长,常用此性质;(2)本题综合考查了矩形的性质、直角三角形斜边上的中线的性质、三角形中
位线的性质,熟记性质并准确识图是解题的关键。
学以致用
例1
学以致用
如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN交
AC于点D.求证:CD=2BD.
A
B
C
M
N
D
例2
学以致用
如图,在△ABC中,∠ACB=90°,∠B=30°,CE垂直于AB于点E,D是AB的中点.
(1)求证:AE=ED;
(2)若AC=2,求BC的长.
例3
学以致用
拓展.如图,在△ABC中,BD、CE是高,M、N分别是BC、ED的中点,试说明:MN⊥DE.
解:连结EM、DM.
∵BD、CE是高,M是BC中点,
∴在Rt△BCE和Rt△BCD中,
∴EM=DM.
又∵N是ED中点,
∴MN⊥ED
N
M
D
E
B
C
A
,
,
BC
2
1
DM
BC
2
1
EM
=
=
性质1
直角三角形两个锐角互余
性质2
直角三角形两直角边的平方和等于斜边的平方(勾股定理)
性质3
直角三角形斜边上的中线等于斜边的一半
性质4
直角三角形中30 °角所对的直角边等于斜边的一半
课堂小结
直角三角形的性质
