22.3 分式方程1 课件 2023-2024学年人教版(五四制)八年级数学上册
文档属性
| 名称 | 22.3 分式方程1 课件 2023-2024学年人教版(五四制)八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 424.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 09:14:06 | ||
图片预览






文档简介
(共15张PPT)
22.3分式方程
情境导入
前面我们已经学过了方程,什么是方程?
什么是方程的解?
什么是一元一次方程?
什么是二元一次方程?
认识新方程
1.相邻两个偶数之比为5:6,求这两个偶数.
2. 小红家与学校相距38km,小红从家去学校总是先乘公共汽车,下车后再步行 2km才能到学校,路途所用时间是 1h. 已知公共汽车的速度是小红步行速度的9倍.求小红步行的速度.
一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间, 与以最大航速逆流航行60千米所用时间相等, 江水的流速为多少
【问题】
解:设江水的流速为v千米/小时,轮船顺流航行速度为————千米/小时,逆流航行速度为_________千米/小时,顺流航行100千米所用的时间为__________小时,逆流航行60千米所用的时间为_________小时.
根据题意,得:
100
20+V
60
20-V
=
100
20+V
60
20-V
(20-V)
(20+V)
这些方程与一元一次方程有什么区别?
一元一次方程的分母中不含有未知数,而这些方程的分母中都含有未知数。
定义:
此方程的分母中含有未知数x,像这样分母中含未知数的方程叫做分式方程.
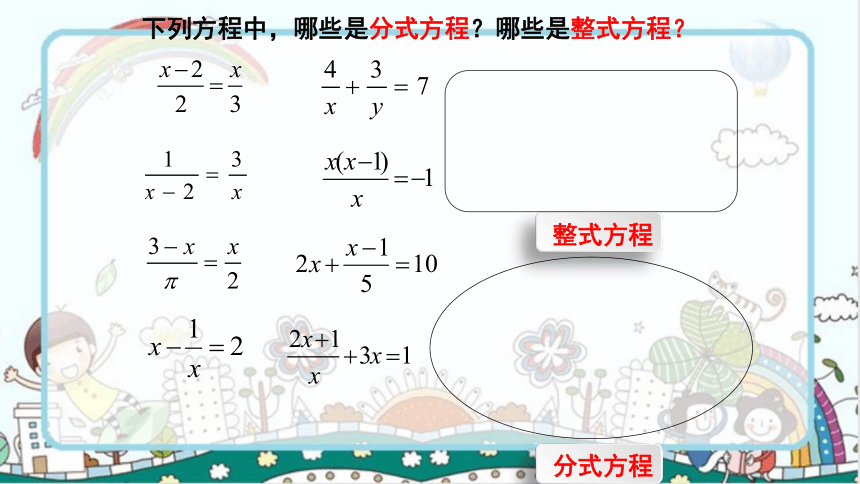
下列方程中,哪些是分式方程?哪些是整式方程?
整式方程
分式方程
课堂练习
7
一队学生去校外参观. 他们出发30分钟时,学校要把一个紧急通知传给带队老师, 派一名学生骑车从学校出发,按原路追赶队伍.若骑车的速度是队伍行进速度的2倍,这名学生追上队伍时离学校的距离是15千米,问这名学生从学校出发到追上队伍用了多少时间?
分析:设这名学生骑车用了xh,则队伍所用的时间为( )h,
路程/km 时间/h 速度/(km/h)
队伍步行
学生骑车
15
15
x
课堂练习
8
路程/km 时间/h 速度/(km/h)
队伍步行
学生骑车
15
15
x
解:设这名学生从学校出发到追上队伍用了xh,则队伍所用的时间为( )h,由题意得:
解得:
经检验: 是原分式方程的解,
答:这名学生从学校出发到追上队伍用了 h.
等量关系为:学生骑车的速度=队伍行进速度×2
小结
7.答:写出答案。
用列表法列分式方程解决实际问题的步骤:
1.审:审题明确已知量和未知量,设未知数为x;
2.列:列表将所需量填写在表格中;
3.找:找出题目中的等量关系;
4.列:根据等量关系列出分式方程;
5.解:解分式方程;
6.验:检验;
理解工程问题的解决方法,正确列出分式方程.并灵活运用工作时间、工作总量、工作效率三者的关系.
工作总量=工作时间×工作效率
工作时间=工作总量÷工作效率
工作效率=工作总量÷工作时间
对点突破一:解分式方程
解:方程两边同乘(x-7),得
x-8+1=8(x-7)
解这个整式方程,得
x=7
经检验,x=7是原分式方程的增根。
所以原分式方程无解
每一项都要乘最简公分母
对点训练一:
解:方程两边同乘(x-2)2,得
x(x-2)-(x-2)2=4
解这个整式方程,得
x=4
经检验,x=4是原分式方程的解
对点突破二:解分式方程
解:方程两边同乘(x+1)(x-1),得
2x-(x-1)=2(x+1)
解这个整式方程,得x=-1
经检验,x=-1 是原分式方程的增根,
所以原分式方程无解
对点训练二:
解:方程两边同乘3(x+1),得
3x=2x+3(x+1)
解这个整式方程,得
经检验, 是原分式方程的解。
谢谢观看
22.3分式方程
情境导入
前面我们已经学过了方程,什么是方程?
什么是方程的解?
什么是一元一次方程?
什么是二元一次方程?
认识新方程
1.相邻两个偶数之比为5:6,求这两个偶数.
2. 小红家与学校相距38km,小红从家去学校总是先乘公共汽车,下车后再步行 2km才能到学校,路途所用时间是 1h. 已知公共汽车的速度是小红步行速度的9倍.求小红步行的速度.
一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间, 与以最大航速逆流航行60千米所用时间相等, 江水的流速为多少
【问题】
解:设江水的流速为v千米/小时,轮船顺流航行速度为————千米/小时,逆流航行速度为_________千米/小时,顺流航行100千米所用的时间为__________小时,逆流航行60千米所用的时间为_________小时.
根据题意,得:
100
20+V
60
20-V
=
100
20+V
60
20-V
(20-V)
(20+V)
这些方程与一元一次方程有什么区别?
一元一次方程的分母中不含有未知数,而这些方程的分母中都含有未知数。
定义:
此方程的分母中含有未知数x,像这样分母中含未知数的方程叫做分式方程.
下列方程中,哪些是分式方程?哪些是整式方程?
整式方程
分式方程
课堂练习
7
一队学生去校外参观. 他们出发30分钟时,学校要把一个紧急通知传给带队老师, 派一名学生骑车从学校出发,按原路追赶队伍.若骑车的速度是队伍行进速度的2倍,这名学生追上队伍时离学校的距离是15千米,问这名学生从学校出发到追上队伍用了多少时间?
分析:设这名学生骑车用了xh,则队伍所用的时间为( )h,
路程/km 时间/h 速度/(km/h)
队伍步行
学生骑车
15
15
x
课堂练习
8
路程/km 时间/h 速度/(km/h)
队伍步行
学生骑车
15
15
x
解:设这名学生从学校出发到追上队伍用了xh,则队伍所用的时间为( )h,由题意得:
解得:
经检验: 是原分式方程的解,
答:这名学生从学校出发到追上队伍用了 h.
等量关系为:学生骑车的速度=队伍行进速度×2
小结
7.答:写出答案。
用列表法列分式方程解决实际问题的步骤:
1.审:审题明确已知量和未知量,设未知数为x;
2.列:列表将所需量填写在表格中;
3.找:找出题目中的等量关系;
4.列:根据等量关系列出分式方程;
5.解:解分式方程;
6.验:检验;
理解工程问题的解决方法,正确列出分式方程.并灵活运用工作时间、工作总量、工作效率三者的关系.
工作总量=工作时间×工作效率
工作时间=工作总量÷工作效率
工作效率=工作总量÷工作时间
对点突破一:解分式方程
解:方程两边同乘(x-7),得
x-8+1=8(x-7)
解这个整式方程,得
x=7
经检验,x=7是原分式方程的增根。
所以原分式方程无解
每一项都要乘最简公分母
对点训练一:
解:方程两边同乘(x-2)2,得
x(x-2)-(x-2)2=4
解这个整式方程,得
x=4
经检验,x=4是原分式方程的解
对点突破二:解分式方程
解:方程两边同乘(x+1)(x-1),得
2x-(x-1)=2(x+1)
解这个整式方程,得x=-1
经检验,x=-1 是原分式方程的增根,
所以原分式方程无解
对点训练二:
解:方程两边同乘3(x+1),得
3x=2x+3(x+1)
解这个整式方程,得
经检验, 是原分式方程的解。
谢谢观看
