2023-2024学年人教版八年级数学上册14.2.1 平方差公式 课件(共16张PPT)
文档属性
| 名称 | 2023-2024学年人教版八年级数学上册14.2.1 平方差公式 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 09:20:45 | ||
图片预览






文档简介
(共16张PPT)
平方差公式
14.2.1
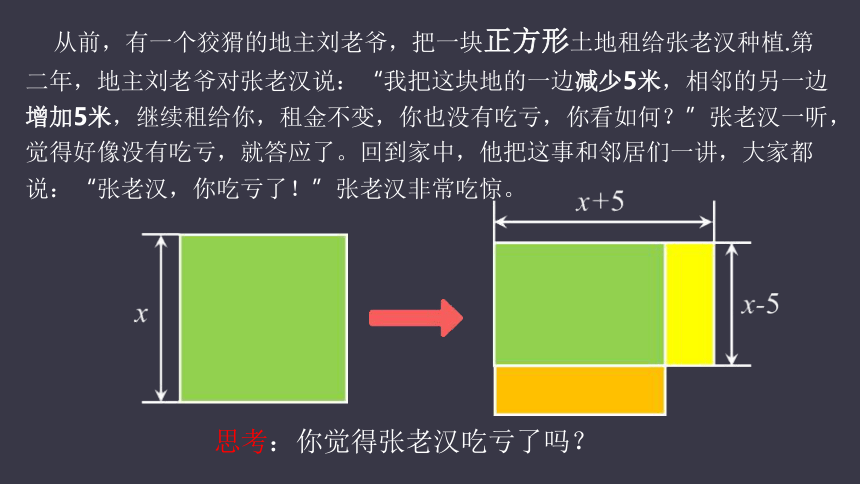
从前,有一个狡猾的地主刘老爷,把一块正方形土地租给张老汉种植.第二年,地主刘老爷对张老汉说:“我把这块地的一边减少5米,相邻的另一边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉一听,觉得好像没有吃亏,就答应了。回到家中,他把这事和邻居们一讲,大家都说:“张老汉,你吃亏了!”张老汉非常吃惊。
思考:你觉得张老汉吃亏了吗?
在一次智力抢答游戏中,主持人提问了两道计算题21×19=?和103×97=?主持人话音刚落,就立刻有一名学生刷地站起来抢答“ 第一题等于399,第二道题等于9991”, 其答题之快,简直就是脱口而出.
思考:你们知道这个学生是如何计算的吗?
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
知识回顾
多项式乘多项式的法则
探究
算一算,比一比,看谁算得又快又准!
观察上述算式,等式左边有什么规律
观察计算结果,你又发现了什么规律
(3)(2x+1)(2x-1)=_______________.
(2)(m+2)(m-2)=_______________;
(1)(x+1)(x-1)=_______________;
探究
(1)计算前﹐算式中都是两个数的_____与这两个数的_____的_____的形式(填“和”“差”“积”);
计算后,计算结果都是前项的______与后项的______的差。
(2)如果用字母a、b分别表示这两个数,你能猜想(a+b)(a-b)的结果是多少吗
(a+b)(a-b)=______
和
差
积
平方
平方
a2-b2
代数法证明
(a+b)(a-b)=a2 - b2
几何法证明
如图,大正方边长是a,小正方形的边长是b
图一中绿色部分的面积可以表示为:
图三中绿色部分的面积可以表示为:
(a+b)(a-b)=
图一
图二
图三
(a+b)(a-b)
几何法证明
图一
图二
图三
如图,大正方边长是a,小正方形的边长是b
图一中绿色部分的面积可以表示为:
图三中绿色部分的面积可以表示为:
(a+b)(a-b)=
(a+b)(a-b)
归纳
归纳公式:(a+b)(a-b)=___________
这个公式叫做乘法的________公式。
文字叙述:
特征:
a2 - b2
两个数的和与这两个数的差的积,等于这两个数的平方差。
平方差
(1)左边是两个二项式相乘,且二项式中有一项完全相同,另一项互为相反数
(2)右边是两项的平方差。
公式中的a、b可以表示数、单项式或多项式。
平方差公式的特征
结构
细节
相同项
相反项
(a+b)(a-b)=a2 - b2
两数之和
两数之差
两数的平方差
技巧
先确定相同项和相反项
例1:
运用平方差公式计算:
(1) (3x+2)(3x-2)
(2) (-x+2y)(-x-2y)
= (3x)2-22
= 9x2-4
解:
(3x+2)(3x-2)
= x2-4y2
= (-x)2-(2y)2
(-x+2y)(-x-2y)
解:
例2:
计算:(1) (y+2)(y-2)-(y-1)(y+5) (2) 102×98
解:
(y+2)(y-2)-(y-1)(y+5)
= y2-22-(y-1)(y+5)
= y2-4-y2-4y+5
= -4y+1
解:
102×98
=(100+2)(100-2)
= 1002-22
= 10000-4
= 9996
从前,有一个狡猾的地主刘老爷,把一块正方形土地租给张老汉种植.第二年,地主刘老爷对张老汉说:“我把这块地的一边减少5米,相邻的另一边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉一听,觉得好像没有吃亏,就答应了。回到家中,他把这事和邻居们一讲,大家都说:“张老汉,你吃亏了!”张老汉非常吃惊。
思考:你觉得张老汉吃亏了吗?
在一次智力抢答游戏中,主持人提问了两道计算题21×19=?和103×97=?主持人话音刚落,就立刻有一名学生刷地站起来抢答“ 第一题等于399,第二道题等于9991”, 其答题之快,简直就是脱口而出 .
思考:你们知道这个学生是如何计算的吗?
21×19=(20+1)(20-1)=(20)2-12=399
103×97=(100+3)(100-3)=(100)2-32=9991
什么是平方差公式?
证明利用平方差公式计算?
平方差公式的结构有什么特点?
平方差公式
平方差公式
14.2.1
从前,有一个狡猾的地主刘老爷,把一块正方形土地租给张老汉种植.第二年,地主刘老爷对张老汉说:“我把这块地的一边减少5米,相邻的另一边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉一听,觉得好像没有吃亏,就答应了。回到家中,他把这事和邻居们一讲,大家都说:“张老汉,你吃亏了!”张老汉非常吃惊。
思考:你觉得张老汉吃亏了吗?
在一次智力抢答游戏中,主持人提问了两道计算题21×19=?和103×97=?主持人话音刚落,就立刻有一名学生刷地站起来抢答“ 第一题等于399,第二道题等于9991”, 其答题之快,简直就是脱口而出.
思考:你们知道这个学生是如何计算的吗?
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
知识回顾
多项式乘多项式的法则
探究
算一算,比一比,看谁算得又快又准!
观察上述算式,等式左边有什么规律
观察计算结果,你又发现了什么规律
(3)(2x+1)(2x-1)=_______________.
(2)(m+2)(m-2)=_______________;
(1)(x+1)(x-1)=_______________;
探究
(1)计算前﹐算式中都是两个数的_____与这两个数的_____的_____的形式(填“和”“差”“积”);
计算后,计算结果都是前项的______与后项的______的差。
(2)如果用字母a、b分别表示这两个数,你能猜想(a+b)(a-b)的结果是多少吗
(a+b)(a-b)=______
和
差
积
平方
平方
a2-b2
代数法证明
(a+b)(a-b)=a2 - b2
几何法证明
如图,大正方边长是a,小正方形的边长是b
图一中绿色部分的面积可以表示为:
图三中绿色部分的面积可以表示为:
(a+b)(a-b)=
图一
图二
图三
(a+b)(a-b)
几何法证明
图一
图二
图三
如图,大正方边长是a,小正方形的边长是b
图一中绿色部分的面积可以表示为:
图三中绿色部分的面积可以表示为:
(a+b)(a-b)=
(a+b)(a-b)
归纳
归纳公式:(a+b)(a-b)=___________
这个公式叫做乘法的________公式。
文字叙述:
特征:
a2 - b2
两个数的和与这两个数的差的积,等于这两个数的平方差。
平方差
(1)左边是两个二项式相乘,且二项式中有一项完全相同,另一项互为相反数
(2)右边是两项的平方差。
公式中的a、b可以表示数、单项式或多项式。
平方差公式的特征
结构
细节
相同项
相反项
(a+b)(a-b)=a2 - b2
两数之和
两数之差
两数的平方差
技巧
先确定相同项和相反项
例1:
运用平方差公式计算:
(1) (3x+2)(3x-2)
(2) (-x+2y)(-x-2y)
= (3x)2-22
= 9x2-4
解:
(3x+2)(3x-2)
= x2-4y2
= (-x)2-(2y)2
(-x+2y)(-x-2y)
解:
例2:
计算:(1) (y+2)(y-2)-(y-1)(y+5) (2) 102×98
解:
(y+2)(y-2)-(y-1)(y+5)
= y2-22-(y-1)(y+5)
= y2-4-y2-4y+5
= -4y+1
解:
102×98
=(100+2)(100-2)
= 1002-22
= 10000-4
= 9996
从前,有一个狡猾的地主刘老爷,把一块正方形土地租给张老汉种植.第二年,地主刘老爷对张老汉说:“我把这块地的一边减少5米,相邻的另一边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉一听,觉得好像没有吃亏,就答应了。回到家中,他把这事和邻居们一讲,大家都说:“张老汉,你吃亏了!”张老汉非常吃惊。
思考:你觉得张老汉吃亏了吗?
在一次智力抢答游戏中,主持人提问了两道计算题21×19=?和103×97=?主持人话音刚落,就立刻有一名学生刷地站起来抢答“ 第一题等于399,第二道题等于9991”, 其答题之快,简直就是脱口而出 .
思考:你们知道这个学生是如何计算的吗?
21×19=(20+1)(20-1)=(20)2-12=399
103×97=(100+3)(100-3)=(100)2-32=9991
什么是平方差公式?
证明利用平方差公式计算?
平方差公式的结构有什么特点?
平方差公式
