2014-2015学年湘教版七年级下册教学课件:第三章 第1节 多项式因式分解(共19张PPT)
文档属性
| 名称 | 2014-2015学年湘教版七年级下册教学课件:第三章 第1节 多项式因式分解(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-17 11:45:56 | ||
图片预览






文档简介
课件19张PPT。3.1多项式因式分解返回21 等于 3 乘哪个整数?21=3×7x2-1等于x+1乘哪个多项式? 对于整数21与3,有整数7使得21=3×7,我们把3叫作21的一个因数. 同理,7也是21的一个因数.对于多项式x2-1与x+1,有x-1使得 ,我们把x+1叫作x2-1的一个因式,同理x-1也是x2-1的一
个因式. 一般地,对于两个多项f与g,如果有多项式h使得
f = gh ,那么我们把g叫作f的一个因式,此时,h也是
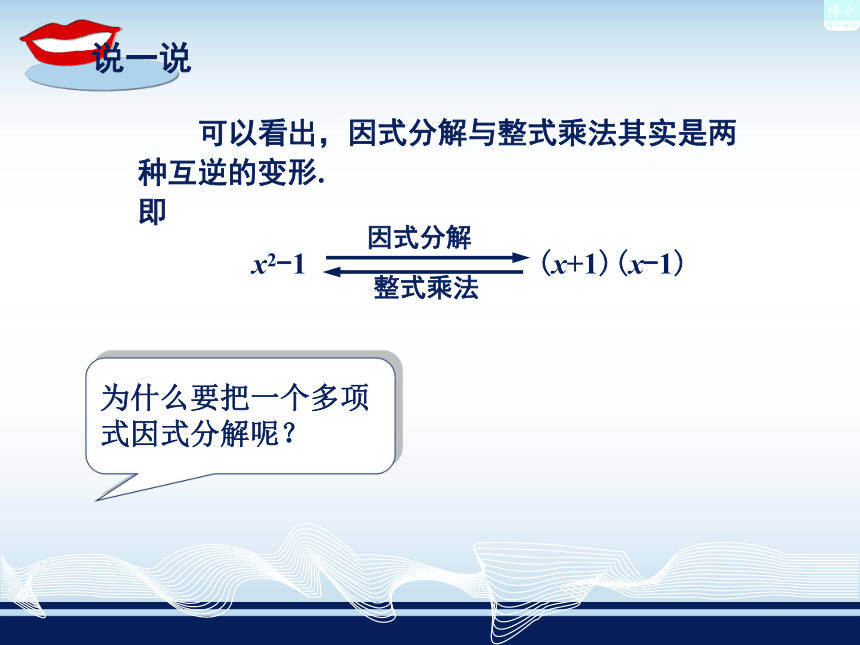
f 的一个因式. 把 x2-1写成 的形式,叫作把 x2-1 因式分解. 一般地,把一个含字母的多项式表示成若干个多项式的乘积的形式,称为把这个多项式因式分解. 可以看出,因式分解与整式乘法其实是两种互逆的变形.
即x2-1(x+1)(x-1)为什么要把一个多项式因式分解呢? 万里长城是由砖砌成的.不少房子也是用砖砌成的. 因此,砖是基本建筑块之一. 类似地,在数学中也经常要寻找那些“基本建筑块”. 例如,在正整数集中,像2,3,5,7,11,13,17,…这些大于1的数,它的因数只有1和它自身,称这样的正整数为质数或素数. 素数就是正整数集中的“基本建筑块”:每一个大于1的正整数都能表示成若干个素数的乘积的形式.例如 12=2×2×3, ①
30=2×3×5 ② 有了①式和②式,就容易求出12和30的最大公因数为2×3=6, 进而很容易把分数 约分:分子与分母同除以6,得 同样地,在系数为有理数(或系数为实数)的多项式组成的集合中,也有一些多项式起着“基本建筑块”的作用: 每一个多项式可以表示成若干个这种多项式的乘积的形式,从而为许多问题的解决架起了桥梁. 例如,以后我们要学习的分式的约分,解一元二次方程,解一元二次不等式等,
都需要把多项式因式分解. 因式分解还可以在许多实际问题中简化计算.例1 下列各式由左边到右边的变形,哪些是因式
分解,哪些不是,为什么?(1)(2)举
例解 (1) 是. 因为从左边到右边是把多项式 a 2+2ab+b 2表示成了多项式a+b与a+b的积的形式.(2) 不是. 因为(m+3)(m-2)+2不是几个多项式乘积的形式.例2 检验下列因式分解是否正确.(1)(2)(3)分析 检验因式分解是否正确,只要看等式右边的几个多项式的乘积与左边的多项式是否相等.举
例解 (1) 因为 x(x + y)=x2+xy,
所以因式分解 x2+ xy = x(x+ y)正确.
(2) 因为(a-2)(a-3)=a2 -5a+6,
所以因式分解 a2 -5a+6=(a-2)(a-3)正确.
(3) 因为(2m-n)(2m+n)=4m2 -n2≠2m2-n2 ,
所以因式分解2m2-n2=(2m-n)(2m+n)不正确.1. 求4,6,14 的最大公因数. 答:最大公因数是2.2. 下列各式由左边到右边的变形,哪些是因式分解,哪些不是,为什么?(1)(2)(3)(4)解 (1) 不是. 因为从左边到右边是整式乘法的过程而不是把多项式表示成几个多项式的积的形式.
(2)是. 因为从左边到右边是把多项式2x2y+4xy2
表示成了多项式 2xy与x+2y 的积的形式.
(3)不是.因为从左边到右边是整式乘法的过程而不是把多项式表示成几个多项式的积的形式.
(4)是. 因为从左边到右边是把多项式4a2-4a+1表示成了多项式2a-1的平方的形式. 一般地,对于两个多项 f 与 g,如果有多项式 h 使得 f = gh ,那么我们把 g 叫作 f 的一个因式,此时,h 也是 f 的一个因式.一般地,把一个含字母的多项式表示成若干个多项式的乘积的形式,称为把这个多项式因式分解.
个因式. 一般地,对于两个多项f与g,如果有多项式h使得
f = gh ,那么我们把g叫作f的一个因式,此时,h也是
f 的一个因式. 把 x2-1写成 的形式,叫作把 x2-1 因式分解. 一般地,把一个含字母的多项式表示成若干个多项式的乘积的形式,称为把这个多项式因式分解. 可以看出,因式分解与整式乘法其实是两种互逆的变形.
即x2-1(x+1)(x-1)为什么要把一个多项式因式分解呢? 万里长城是由砖砌成的.不少房子也是用砖砌成的. 因此,砖是基本建筑块之一. 类似地,在数学中也经常要寻找那些“基本建筑块”. 例如,在正整数集中,像2,3,5,7,11,13,17,…这些大于1的数,它的因数只有1和它自身,称这样的正整数为质数或素数. 素数就是正整数集中的“基本建筑块”:每一个大于1的正整数都能表示成若干个素数的乘积的形式.例如 12=2×2×3, ①
30=2×3×5 ② 有了①式和②式,就容易求出12和30的最大公因数为2×3=6, 进而很容易把分数 约分:分子与分母同除以6,得 同样地,在系数为有理数(或系数为实数)的多项式组成的集合中,也有一些多项式起着“基本建筑块”的作用: 每一个多项式可以表示成若干个这种多项式的乘积的形式,从而为许多问题的解决架起了桥梁. 例如,以后我们要学习的分式的约分,解一元二次方程,解一元二次不等式等,
都需要把多项式因式分解. 因式分解还可以在许多实际问题中简化计算.例1 下列各式由左边到右边的变形,哪些是因式
分解,哪些不是,为什么?(1)(2)举
例解 (1) 是. 因为从左边到右边是把多项式 a 2+2ab+b 2表示成了多项式a+b与a+b的积的形式.(2) 不是. 因为(m+3)(m-2)+2不是几个多项式乘积的形式.例2 检验下列因式分解是否正确.(1)(2)(3)分析 检验因式分解是否正确,只要看等式右边的几个多项式的乘积与左边的多项式是否相等.举
例解 (1) 因为 x(x + y)=x2+xy,
所以因式分解 x2+ xy = x(x+ y)正确.
(2) 因为(a-2)(a-3)=a2 -5a+6,
所以因式分解 a2 -5a+6=(a-2)(a-3)正确.
(3) 因为(2m-n)(2m+n)=4m2 -n2≠2m2-n2 ,
所以因式分解2m2-n2=(2m-n)(2m+n)不正确.1. 求4,6,14 的最大公因数. 答:最大公因数是2.2. 下列各式由左边到右边的变形,哪些是因式分解,哪些不是,为什么?(1)(2)(3)(4)解 (1) 不是. 因为从左边到右边是整式乘法的过程而不是把多项式表示成几个多项式的积的形式.
(2)是. 因为从左边到右边是把多项式2x2y+4xy2
表示成了多项式 2xy与x+2y 的积的形式.
(3)不是.因为从左边到右边是整式乘法的过程而不是把多项式表示成几个多项式的积的形式.
(4)是. 因为从左边到右边是把多项式4a2-4a+1表示成了多项式2a-1的平方的形式. 一般地,对于两个多项 f 与 g,如果有多项式 h 使得 f = gh ,那么我们把 g 叫作 f 的一个因式,此时,h 也是 f 的一个因式.一般地,把一个含字母的多项式表示成若干个多项式的乘积的形式,称为把这个多项式因式分解.
