人教版四年级下册数学三角形的内角和(课件)(共18张PPT)
文档属性
| 名称 | 人教版四年级下册数学三角形的内角和(课件)(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 17:04:27 | ||
图片预览





文档简介
(共18张PPT)
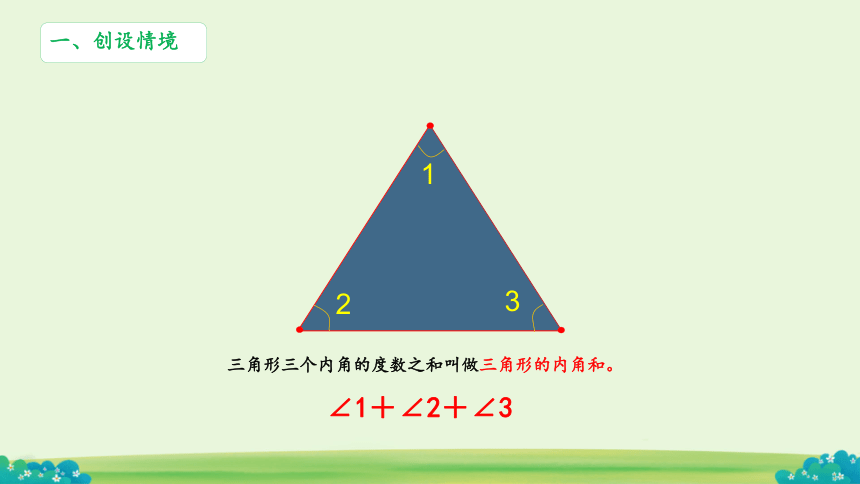
一、创设情境
三角形三个内角的度数之和叫做三角形的内角和。
1
2
3
∠1+∠2+∠3
到底谁的内角和大呢?
二、自主探究 合作交流
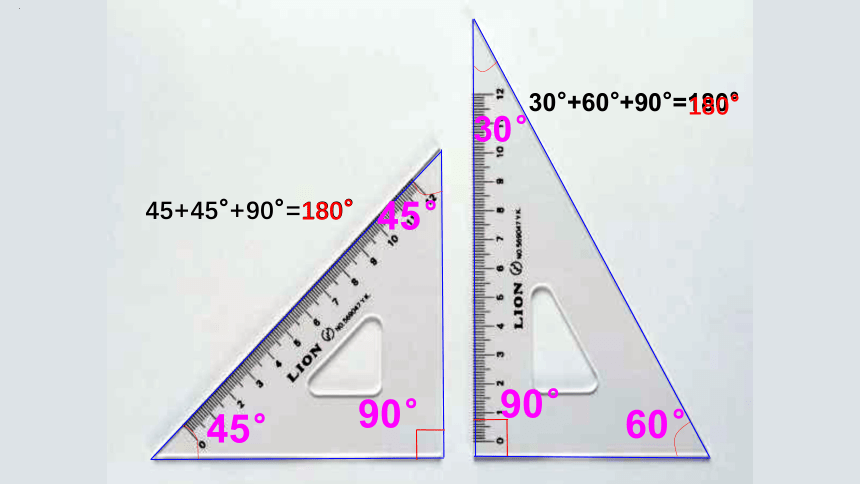
拿出一副三角尺,同桌之间互相说一说每个三角尺上3个角的度数,并分别求出这两个三角形的内角和。
45°
45°
30°
60°
90°
90°
45+45°+90°=180°
30°+60°+90°=180°
180°
180°
二、自主探究 合作交流
1、其他三角形的内角和是多少度呢?
2、是不是所有的三角形的内角和都是180°呢?
猜想:180°
能用什么方法来证明吗?
1.组长拿出准备好的直角三角形、
锐角三角形和钝角三角形学具各一个;
2.用量角器量出每个内角的度数;
3.求出每个三角形的内角和;
4.把结果记录在表格中。
(活动1)测量验证:
二、自主探究 合作交流
三角形 每个内角的度数 内角和
测量法
1.组长拿出准备好的直角三角形、锐角三角形
和钝角三角形学具各一个;
2.把每个三角形的三个内角剪下来,再拼在一起;(注:剪之前标注好角的序号哦!)
3.可以拼成一个什么角?
(活动2)剪拼验证:小组合作
3
平角:1800
平角:1800
平角:1800
剪拼法
锐角三角形
钝角三角形
直角三角形
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
折拼法
从中我们可以得出
一个怎样的结论?
我们的内角和一样大,都是180° 。
三、应用规律 解决问题
1、在一个三角形中,∠1=1400,∠3=250 ,
求∠2的度数。
∠2=180°-∠1-∠3
=180°-140°-25°
=25°
第一关
2、一个等腰三角形的风筝,它的一个底角 70°, 它的顶角是多少度?
方法一: 180°-70°-70°=40°
方法二: 180°-70°×2=40°
答:它的顶角是40°。
第二关
3、把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度
因为:三角形的内角和是180°,
所以:这个三角形沿虚线剪成两个小三角形,
每个小三角形的内角和也是180°。
第三关
通过本节课的学习,你有什么收获?
金字塔代表了目标和希望,希望同学们通过不断地学习,达到属于自己的金字塔尖。
一、创设情境
三角形三个内角的度数之和叫做三角形的内角和。
1
2
3
∠1+∠2+∠3
到底谁的内角和大呢?
二、自主探究 合作交流
拿出一副三角尺,同桌之间互相说一说每个三角尺上3个角的度数,并分别求出这两个三角形的内角和。
45°
45°
30°
60°
90°
90°
45+45°+90°=180°
30°+60°+90°=180°
180°
180°
二、自主探究 合作交流
1、其他三角形的内角和是多少度呢?
2、是不是所有的三角形的内角和都是180°呢?
猜想:180°
能用什么方法来证明吗?
1.组长拿出准备好的直角三角形、
锐角三角形和钝角三角形学具各一个;
2.用量角器量出每个内角的度数;
3.求出每个三角形的内角和;
4.把结果记录在表格中。
(活动1)测量验证:
二、自主探究 合作交流
三角形 每个内角的度数 内角和
测量法
1.组长拿出准备好的直角三角形、锐角三角形
和钝角三角形学具各一个;
2.把每个三角形的三个内角剪下来,再拼在一起;(注:剪之前标注好角的序号哦!)
3.可以拼成一个什么角?
(活动2)剪拼验证:小组合作
3
平角:1800
平角:1800
平角:1800
剪拼法
锐角三角形
钝角三角形
直角三角形
2
1
2
2
3
3
钝角三角形
1
1
1
3
3
锐角三角形
1
1
2
2
3
3
直角三角形
2
折拼法
从中我们可以得出
一个怎样的结论?
我们的内角和一样大,都是180° 。
三、应用规律 解决问题
1、在一个三角形中,∠1=1400,∠3=250 ,
求∠2的度数。
∠2=180°-∠1-∠3
=180°-140°-25°
=25°
第一关
2、一个等腰三角形的风筝,它的一个底角 70°, 它的顶角是多少度?
方法一: 180°-70°-70°=40°
方法二: 180°-70°×2=40°
答:它的顶角是40°。
第二关
3、把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度
因为:三角形的内角和是180°,
所以:这个三角形沿虚线剪成两个小三角形,
每个小三角形的内角和也是180°。
第三关
通过本节课的学习,你有什么收获?
金字塔代表了目标和希望,希望同学们通过不断地学习,达到属于自己的金字塔尖。
