高二数学之圆锥曲线培优专题 双曲线 学案
文档属性
| 名称 | 高二数学之圆锥曲线培优专题 双曲线 学案 | 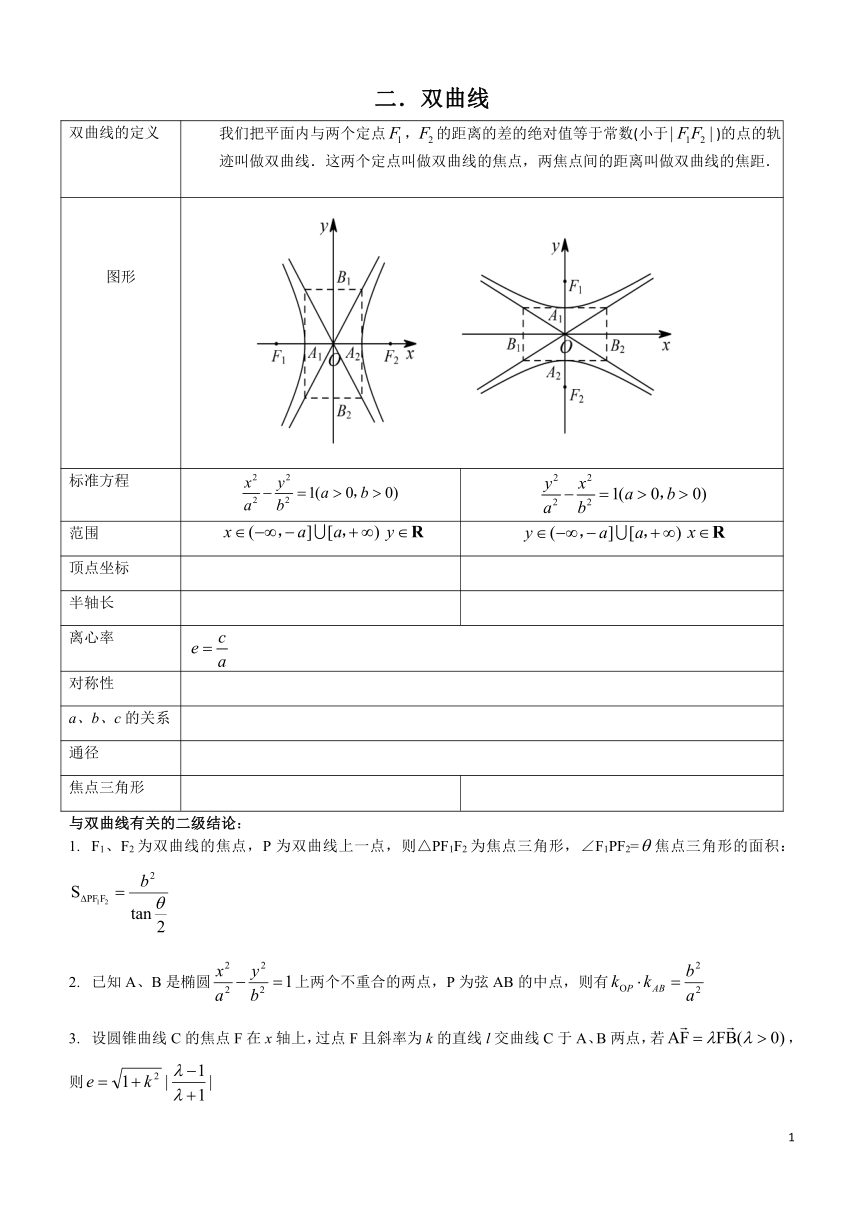 | |
| 格式 | |||
| 文件大小 | 445.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 21:54:37 | ||
图片预览




文档简介
二.双曲线
双曲线的定义 我们把平面内与两个定点 F1,F2 的距离的差的绝对值等于常数(小于 | F1F2 | )的点的轨
迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
图形
标准方程 x2 y2 2 2
2 2 1(a 0,b 0)
y x
2 2 1(a 0,b 0)a b a b
范围 x ( , a] [a, ) y R y ( , a] [a, ) x R
顶点坐标
半轴长
离心率 e c
a
对称性
a、b、c的关系
通径
焦点三角形
与双曲线有关的二级结论:
1. F1、F2 为双曲线的焦点,P 为双曲线上一点,则△PF1F2 为焦点三角形,∠F1PF2= 焦点三角形的面积:
S b
2
PF1F
2
tan
2
x2 y2 b2
2. 已知 A、B 是椭圆 2 2 1上两个不重合的两点,P 为弦 AB 的中点,则有 kOP ka b AB
a2
3. 设圆锥曲线 C 的焦点 F 在 x轴上,过点 F 且斜率为 k的直线 l交曲线 C 于 A、B 两点,若AF FB( 0),
则 e 1 k 2 | 1 |
1
1
x2 y2 xx yy
4. 过椭圆外一点 P(x0,y0)作椭圆 2 2 1的切线,则切点弦的方程为
0 02 1a b a b2
双曲线基本运算
x2 2
例 1 焦点为(0,6),且与双曲线 y 1有相同的渐近线的双曲线方程是( )
2
x2 y2 y2 x2 2 2 2 2
A. 1 B. 1 y x x yC. 1 D. 1
12 24 12 24 24 12 24 12
x2 2
例 2 双曲线 y 1的顶点到其渐近线的距离等于( )
4
2 4 2 5 4 5
A. B. C. D.
5 5 5 5
x2 y2 5
例 3 双曲线 C: 2 2 1的离心率为 ,则 C 的渐近线方程为( )a b 2
1 1 1
A. y= x B. y= x C. y= x D.y= x
4 3 2
0 x
2 y2 y2 x2
例 4 已知 ,则双曲线 C1: 2 1与 C2: 1的( )4 cos sin 2 sin 2 cos2
A.实轴长相等 B.虚轴长相等 C.焦距相等 D.离心率相等
离心率问题
x2 y2 3 x2 y2
例 1 若椭圆 2 2 1的离心率为 ,则双曲线 2 2 1的离心率为( )a b 2 a b
5 5 3 5
A. B. C. D.
4 2 2 4
2
x2 y2
例 2 双曲线 2 2 1的左右焦点分别为 F1、F2,过 F1 作倾斜角为 30°的直线交双曲线右支于 M 点,若 MF2a b
垂直于 x轴,则双曲线的离心率为( )
3
A. 6 B. 3 C. 2 D.
3
例 3 已知 F1、F2 是双曲线的两个焦点,以线段 F1F2 为边作正三角形 MF1F2,若边 MF1的中点在双曲线上,则
双曲线的离心率为( )
3 1
A. 4 2 3 B. 3 1 C. D. 3 1
2
2 2
例 4 设直线 x 3y m 0(m 0) x y与双曲线 2 2 1两条渐近线分别交于点 A、B,若点 P(m,0)满足 PA=PB,a b
则该双曲线的离心率为______
x2 y2
例 5 双曲线 2 2 1的两个焦点为 F1、F2,若 P 为其上一点,且 PF1=2PF2,则双曲线离心率的取值范围是( )a b
A. (1,3) B.(1,3] C.(3,+ ) D.[3,+ )
C x
2
6 F F : +y 2例 如图, 1、 2是椭圆 1 1与双曲线 C2 的公共焦点,A、B 分别是 C1,C2 在第二、四象限的公4
共点,若四边形 AF1BF2为矩形,则 C2 的离心率为( )
A. 2 B. 3
3 6
C. D.
2 2
3
例 7 已知 F1、F2是两个定点,点 P 是以 F1 和 F2为公共焦点的椭圆和双曲线的一个交点,并且 PF1⊥PF2,e1,e2
分别是上述椭圆和双曲线的离心率,则有( )
1 1 1 1
A. 2 2 4 B. 2 e e e e2
2
1 2 1 2
C. e21 e
2
2 4 D. e
2
1 e
2
2 2
例 8 已知 F1、F2 是椭圆和双曲线的公共焦点,P 是他们的一个公共点,且∠F1PF2= ,则椭圆和双曲线的离心
3
率的倒数之和的最大值为( )
4 3 2 3
A. B. C.3 D.2
3 3
x2 y2
例 9 已知双曲线 2 2 1的右焦点为 F,若过点 F 且倾斜角为 60°的直线与双曲线的右支有且只一个交点,a b
则此双曲线的离心率的取值范围是( )
A.(1,2] B.(1,2) C.[2,+ ) D.(2,+ )
x2 y2
例 10 斜率为 2 的直线 l 过双曲线 2 2 1的右焦点 F 且与双曲线的左右两支分别相交,则双曲线离心率的a b
取值范围是( )
A.(1,2) B.(1, 3 ) C.(1, 5 ) D.( 5 ,+ )
x2 y2
例 11 F1、F2 是双曲线 C: 2 2 1的两个焦点,P 是 C 上一点,若 PF1+PF2=6a,且△PF1F2的最小内角为 30°,a b
则 C 的离心率为________
4
双曲线有关的最值
y2
例 1 2若点 A 坐标为(2,2),F2是双曲线 x 1的右焦点,点 P 为双曲线的动点,则
3
(1)P 在双曲线右支,则 PA-PF2 的范围是_____________
(2)P 在双曲线左支,则 PA+PF2 的最大值是____________
x2 y2
例 2 已知 F是双曲线 1的左焦点,P是双曲线右支上的动点,若 A(1, 4),则 | PF | | PA | 的最小值
4 12
是__________.
x2 y2
例 3 2 2已知点 P为双曲线 1右支上的一点,M,N分别是圆 (x 5) y 4 和 (x 5)2 y2 1上的点,
9 16
则 | PM | | PN |的最大值为__________.
多选压轴题
x2 y2
(多选)1.已知 F1,F2 分别为双曲线 2 2 1(a>0,b>0)的左、右焦点,过点 F2 的直线与双曲线的a b
右支交于 A,B两点,记△AF1F2 的内切圆 O1 的半径为 r1,△BF1F2 的内切圆 O2 的半径为 r2.若双曲线的离
心率 e=2,则下列说法正确的是( )
A.以 O1O2 为直径的圆与直线 AB相切
B.r1r2=a2
C.O1,O2 在直线 x=a上
D.r1+r2 的范围是[2a,2 3a)
5
y22
(多选)2.如图,O为坐标原点,F1,F2 分别为双曲线 C: x 2 1的左、右焦点,过双曲线 C右支上一b
点 P作双曲线的切线 l分别交两渐近线于 A、B两点,交 x轴于点 D,则下列结论正确的是( )
A.|AB|min=2b
B.S△AOB=2S△AOP
C.S△AOB=2b
D.若存在点 P,使得S PF F 15 ,且F1D 2DF2 ,1 2
6
则双曲线 C的离心率为 2 或
2
x2 y2
(多选)3.已知 F1,F2 分别为双曲线 C: 2 2 1(a>0,b>0)的左、右焦点,P为双曲线 C的渐近线a b
在第一象限部分上的一点,线段 PF2 与双曲线交点为 Q,且|F1P|=|F1F2|=2|PF2|,O为坐标原点,则下列结
论正确的是( )
2 3
A.|OP|=2a B.双曲线 C的离心率 e=
3
12 6 x2 y2
C.|QF1|= a D.若△QF1F2 的内心的横坐标为 3,则双曲线 C的方程为 1
3 9 15
6
x2 y2
(多选)4.已知双曲线Γ: 2 2 1(a>0,b>0),左焦点为 F,左右顶点分别为 A1、A2,B(0,b),a b
P是Γ右支上一动点,且|PF|+|PB|的最小值为( 3 +2)a,P关于 x轴的对称点为 Q,则下列结论正确的是
( )
A.Γ的离心率为 2 B.PA2⊥A1Q
C.sin∠QPA1=sin∠QA2A1 D.4|PB|≥ 6 |PQ|
x2 y2 15 1 2 3
(多选)5.已知 F1,F2 是双曲线 C: 2 2 1的左、右焦点,A( , )是 C上一点,若 C的离心率为 ,a b 2 2 3
连结 AF2 交 C于点 B,则( )
x2
A 2.C的方程为 y 1
3
B.∠F1AF2=90°
C.△F1AF2 的周长为 2 5 2
D.△ABF1 的内切圆半径为 5 3
x2 y2
(多选)6.双曲线 C: 1的左、右焦点分别为 F1,F2,过点 F2 的直线与双曲线右支交于 A、B两点,
4 5
△AF1F2 和△BF1F2 内切圆半径分别为 r1 和 r2,则( )
A.双曲线 C的渐近线方程为 2x± 5 y=0
B.△AF1B面积的最小值为 15
C.△AF1F2 和△BF1F2 内切圆圆心的连线与 x轴垂直
D.r1 r2 为定值 1
7
x2 y2
(多选)7.双曲线 C: 2 2 1的左、右焦点分别为 F1,F2,倾斜角为 60°的直线 l过双曲线 C的右焦点a b
F2,与双曲线 C右支交于 A,B两点,且AF2 5F2B,则( )
A.双曲线 C的离心率为 2
B.△AF1F2 与△BF1F2 内切圆半径比为 3:1
C.△AF1F2 与△BF1F2 周长之比为 4:1
D.△AF1F2 与△BF1F2 面积之比为 5:1
x2 y2
(多选)8.若双曲线 C: 1,F1,F2 分别为左、右焦点,设点 P在双曲线上且在第一象限的动点,
4 5
点 I为△PF1F2 的内心,点 G为△PF1F2 的重心,则下列说法正确的是( )
3
A.双曲线 C的离心率为
2
B.点 I的运动轨迹为双曲线的一部分
2
C.若|PF1|=2|PF2|,PI xPF1 yPF2 ,则 y﹣x= 9
D.存在点 P,使得 IG∥F1F2
8
参考答案
双曲线基本运算
1. B 2.C 3.C 4.C
离心率问题
5
1. B 2.B 3.D 4. 5.B 6.D 7.B 8.A 9.C 10.D 11. 3
2
双曲线有关的最值
1. (1)[-1,2] (2)2 5 +4 2.9 3.9
多选压轴
1.ABC 2.AB 3.ACD 4.BCD 5.ABD 6.BCD 7.BD 8.ACD
9
双曲线的定义 我们把平面内与两个定点 F1,F2 的距离的差的绝对值等于常数(小于 | F1F2 | )的点的轨
迹叫做双曲线.这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
图形
标准方程 x2 y2 2 2
2 2 1(a 0,b 0)
y x
2 2 1(a 0,b 0)a b a b
范围 x ( , a] [a, ) y R y ( , a] [a, ) x R
顶点坐标
半轴长
离心率 e c
a
对称性
a、b、c的关系
通径
焦点三角形
与双曲线有关的二级结论:
1. F1、F2 为双曲线的焦点,P 为双曲线上一点,则△PF1F2 为焦点三角形,∠F1PF2= 焦点三角形的面积:
S b
2
PF1F
2
tan
2
x2 y2 b2
2. 已知 A、B 是椭圆 2 2 1上两个不重合的两点,P 为弦 AB 的中点,则有 kOP ka b AB
a2
3. 设圆锥曲线 C 的焦点 F 在 x轴上,过点 F 且斜率为 k的直线 l交曲线 C 于 A、B 两点,若AF FB( 0),
则 e 1 k 2 | 1 |
1
1
x2 y2 xx yy
4. 过椭圆外一点 P(x0,y0)作椭圆 2 2 1的切线,则切点弦的方程为
0 02 1a b a b2
双曲线基本运算
x2 2
例 1 焦点为(0,6),且与双曲线 y 1有相同的渐近线的双曲线方程是( )
2
x2 y2 y2 x2 2 2 2 2
A. 1 B. 1 y x x yC. 1 D. 1
12 24 12 24 24 12 24 12
x2 2
例 2 双曲线 y 1的顶点到其渐近线的距离等于( )
4
2 4 2 5 4 5
A. B. C. D.
5 5 5 5
x2 y2 5
例 3 双曲线 C: 2 2 1的离心率为 ,则 C 的渐近线方程为( )a b 2
1 1 1
A. y= x B. y= x C. y= x D.y= x
4 3 2
0 x
2 y2 y2 x2
例 4 已知 ,则双曲线 C1: 2 1与 C2: 1的( )4 cos sin 2 sin 2 cos2
A.实轴长相等 B.虚轴长相等 C.焦距相等 D.离心率相等
离心率问题
x2 y2 3 x2 y2
例 1 若椭圆 2 2 1的离心率为 ,则双曲线 2 2 1的离心率为( )a b 2 a b
5 5 3 5
A. B. C. D.
4 2 2 4
2
x2 y2
例 2 双曲线 2 2 1的左右焦点分别为 F1、F2,过 F1 作倾斜角为 30°的直线交双曲线右支于 M 点,若 MF2a b
垂直于 x轴,则双曲线的离心率为( )
3
A. 6 B. 3 C. 2 D.
3
例 3 已知 F1、F2 是双曲线的两个焦点,以线段 F1F2 为边作正三角形 MF1F2,若边 MF1的中点在双曲线上,则
双曲线的离心率为( )
3 1
A. 4 2 3 B. 3 1 C. D. 3 1
2
2 2
例 4 设直线 x 3y m 0(m 0) x y与双曲线 2 2 1两条渐近线分别交于点 A、B,若点 P(m,0)满足 PA=PB,a b
则该双曲线的离心率为______
x2 y2
例 5 双曲线 2 2 1的两个焦点为 F1、F2,若 P 为其上一点,且 PF1=2PF2,则双曲线离心率的取值范围是( )a b
A. (1,3) B.(1,3] C.(3,+ ) D.[3,+ )
C x
2
6 F F : +y 2例 如图, 1、 2是椭圆 1 1与双曲线 C2 的公共焦点,A、B 分别是 C1,C2 在第二、四象限的公4
共点,若四边形 AF1BF2为矩形,则 C2 的离心率为( )
A. 2 B. 3
3 6
C. D.
2 2
3
例 7 已知 F1、F2是两个定点,点 P 是以 F1 和 F2为公共焦点的椭圆和双曲线的一个交点,并且 PF1⊥PF2,e1,e2
分别是上述椭圆和双曲线的离心率,则有( )
1 1 1 1
A. 2 2 4 B. 2 e e e e2
2
1 2 1 2
C. e21 e
2
2 4 D. e
2
1 e
2
2 2
例 8 已知 F1、F2 是椭圆和双曲线的公共焦点,P 是他们的一个公共点,且∠F1PF2= ,则椭圆和双曲线的离心
3
率的倒数之和的最大值为( )
4 3 2 3
A. B. C.3 D.2
3 3
x2 y2
例 9 已知双曲线 2 2 1的右焦点为 F,若过点 F 且倾斜角为 60°的直线与双曲线的右支有且只一个交点,a b
则此双曲线的离心率的取值范围是( )
A.(1,2] B.(1,2) C.[2,+ ) D.(2,+ )
x2 y2
例 10 斜率为 2 的直线 l 过双曲线 2 2 1的右焦点 F 且与双曲线的左右两支分别相交,则双曲线离心率的a b
取值范围是( )
A.(1,2) B.(1, 3 ) C.(1, 5 ) D.( 5 ,+ )
x2 y2
例 11 F1、F2 是双曲线 C: 2 2 1的两个焦点,P 是 C 上一点,若 PF1+PF2=6a,且△PF1F2的最小内角为 30°,a b
则 C 的离心率为________
4
双曲线有关的最值
y2
例 1 2若点 A 坐标为(2,2),F2是双曲线 x 1的右焦点,点 P 为双曲线的动点,则
3
(1)P 在双曲线右支,则 PA-PF2 的范围是_____________
(2)P 在双曲线左支,则 PA+PF2 的最大值是____________
x2 y2
例 2 已知 F是双曲线 1的左焦点,P是双曲线右支上的动点,若 A(1, 4),则 | PF | | PA | 的最小值
4 12
是__________.
x2 y2
例 3 2 2已知点 P为双曲线 1右支上的一点,M,N分别是圆 (x 5) y 4 和 (x 5)2 y2 1上的点,
9 16
则 | PM | | PN |的最大值为__________.
多选压轴题
x2 y2
(多选)1.已知 F1,F2 分别为双曲线 2 2 1(a>0,b>0)的左、右焦点,过点 F2 的直线与双曲线的a b
右支交于 A,B两点,记△AF1F2 的内切圆 O1 的半径为 r1,△BF1F2 的内切圆 O2 的半径为 r2.若双曲线的离
心率 e=2,则下列说法正确的是( )
A.以 O1O2 为直径的圆与直线 AB相切
B.r1r2=a2
C.O1,O2 在直线 x=a上
D.r1+r2 的范围是[2a,2 3a)
5
y22
(多选)2.如图,O为坐标原点,F1,F2 分别为双曲线 C: x 2 1的左、右焦点,过双曲线 C右支上一b
点 P作双曲线的切线 l分别交两渐近线于 A、B两点,交 x轴于点 D,则下列结论正确的是( )
A.|AB|min=2b
B.S△AOB=2S△AOP
C.S△AOB=2b
D.若存在点 P,使得S PF F 15 ,且F1D 2DF2 ,1 2
6
则双曲线 C的离心率为 2 或
2
x2 y2
(多选)3.已知 F1,F2 分别为双曲线 C: 2 2 1(a>0,b>0)的左、右焦点,P为双曲线 C的渐近线a b
在第一象限部分上的一点,线段 PF2 与双曲线交点为 Q,且|F1P|=|F1F2|=2|PF2|,O为坐标原点,则下列结
论正确的是( )
2 3
A.|OP|=2a B.双曲线 C的离心率 e=
3
12 6 x2 y2
C.|QF1|= a D.若△QF1F2 的内心的横坐标为 3,则双曲线 C的方程为 1
3 9 15
6
x2 y2
(多选)4.已知双曲线Γ: 2 2 1(a>0,b>0),左焦点为 F,左右顶点分别为 A1、A2,B(0,b),a b
P是Γ右支上一动点,且|PF|+|PB|的最小值为( 3 +2)a,P关于 x轴的对称点为 Q,则下列结论正确的是
( )
A.Γ的离心率为 2 B.PA2⊥A1Q
C.sin∠QPA1=sin∠QA2A1 D.4|PB|≥ 6 |PQ|
x2 y2 15 1 2 3
(多选)5.已知 F1,F2 是双曲线 C: 2 2 1的左、右焦点,A( , )是 C上一点,若 C的离心率为 ,a b 2 2 3
连结 AF2 交 C于点 B,则( )
x2
A 2.C的方程为 y 1
3
B.∠F1AF2=90°
C.△F1AF2 的周长为 2 5 2
D.△ABF1 的内切圆半径为 5 3
x2 y2
(多选)6.双曲线 C: 1的左、右焦点分别为 F1,F2,过点 F2 的直线与双曲线右支交于 A、B两点,
4 5
△AF1F2 和△BF1F2 内切圆半径分别为 r1 和 r2,则( )
A.双曲线 C的渐近线方程为 2x± 5 y=0
B.△AF1B面积的最小值为 15
C.△AF1F2 和△BF1F2 内切圆圆心的连线与 x轴垂直
D.r1 r2 为定值 1
7
x2 y2
(多选)7.双曲线 C: 2 2 1的左、右焦点分别为 F1,F2,倾斜角为 60°的直线 l过双曲线 C的右焦点a b
F2,与双曲线 C右支交于 A,B两点,且AF2 5F2B,则( )
A.双曲线 C的离心率为 2
B.△AF1F2 与△BF1F2 内切圆半径比为 3:1
C.△AF1F2 与△BF1F2 周长之比为 4:1
D.△AF1F2 与△BF1F2 面积之比为 5:1
x2 y2
(多选)8.若双曲线 C: 1,F1,F2 分别为左、右焦点,设点 P在双曲线上且在第一象限的动点,
4 5
点 I为△PF1F2 的内心,点 G为△PF1F2 的重心,则下列说法正确的是( )
3
A.双曲线 C的离心率为
2
B.点 I的运动轨迹为双曲线的一部分
2
C.若|PF1|=2|PF2|,PI xPF1 yPF2 ,则 y﹣x= 9
D.存在点 P,使得 IG∥F1F2
8
参考答案
双曲线基本运算
1. B 2.C 3.C 4.C
离心率问题
5
1. B 2.B 3.D 4. 5.B 6.D 7.B 8.A 9.C 10.D 11. 3
2
双曲线有关的最值
1. (1)[-1,2] (2)2 5 +4 2.9 3.9
多选压轴
1.ABC 2.AB 3.ACD 4.BCD 5.ABD 6.BCD 7.BD 8.ACD
9
