7.2.2三角形的外角
图片预览



文档简介
课件17张PPT。7.2.2三角形的外角2、在△ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .1、三角形三个内角的和等于多少度?知识回顾3、在△ABC中,
∠A:∠B:∠C=2:3:4,则∠A= ,
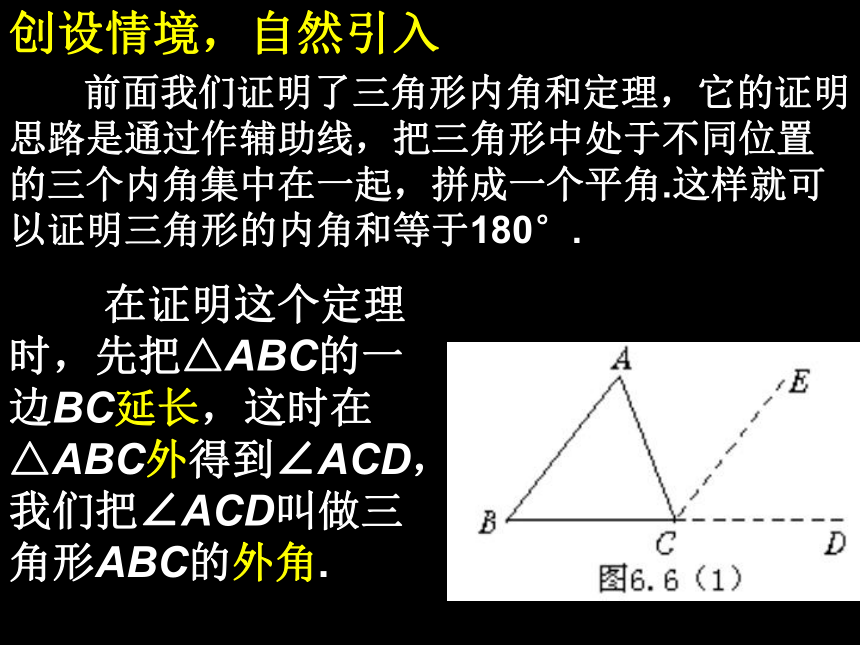
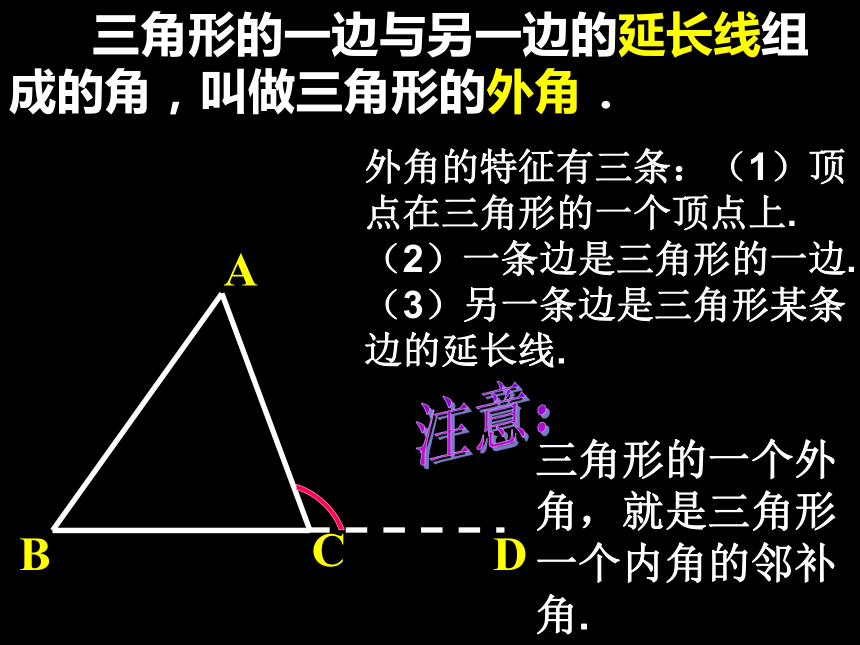
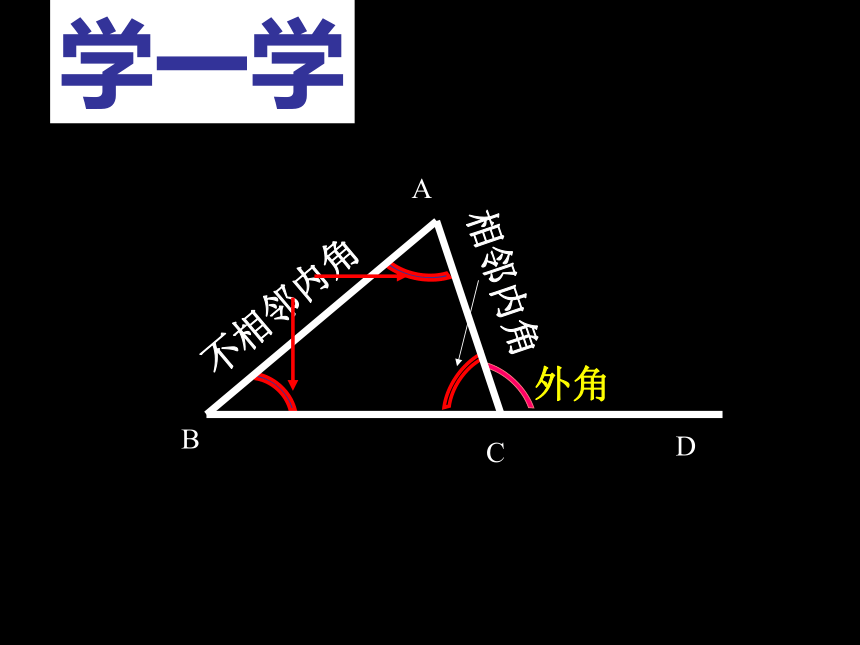
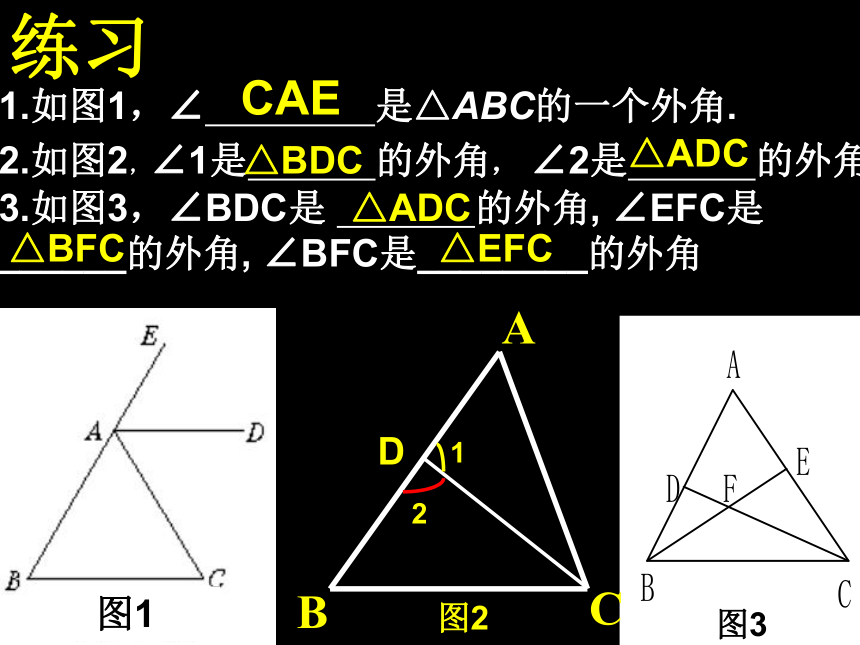
∠B= , ∠C= . 40°60°80°65°60°创设情境,自然引入 前面我们证明了三角形内角和定理,它的证明思路是通过作辅助线,把三角形中处于不同位置的三个内角集中在一起,拼成一个平角.这样就可以证明三角形的内角和等于180°. 在证明这个定理时,先把△ABC的一边BC延长,这时在△ABC外得到∠ACD,我们把∠ACD叫做三角形ABC的外角.D 三角形的一边与另一边的延长线组成的角,叫做三角形的外角.外角的特征有三条:(1)顶点在三角形的一个顶点上. (2)一条边是三角形的一边. (3)另一条边是三角形某条边的延长线. 三角形的一个外角,就是三角形一个内角的邻补角.注意:外角不相邻内角相邻内角ABCD学一学画图并思考: 画一个△ABC ,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?归纳:每一个三角形都有6个外角. 每一个顶点相对应的外角都有2个.它们是对顶角.因此相等.每个外角与相邻的内角是邻补角. 把三角形各边向两方延长,就可以画出一个三角形所有的外角. 练习1.如图1,∠ 是△ABC的一个外角.2.图1图22.如图2,∠1是 的外角, ∠2是 的外角.3.如图3,∠BDC是 的外角, ∠EFC是______的外角, ∠BFC是________的外角图3CAE△BDC△ADC△ADC△BFC△EFC2.图中若∠A=70°,∠B=60o,试求∠ACD的度数.并说出你的理由.如果能, ∠ACD与∠A, ∠B有什么关系?1. 图中哪些角是三角形的内角,哪些角是三角形的外角?∠ACD= 130°∠ACD=∠A+ ∠B∠ACD>∠A∠ACD>∠B任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?结论:3、三角形的一个外角大于与它不相邻的任何一个内角。2、三角形的一个外角等于与它不相邻的两个内角的和;1、三角形的一个外角与它相邻的内角互补;三角形的外角与内角的关系:范例 例1、如图,∠BAE,∠CBF ,∠ACD是△ABC的三个外角,它们的和是多少? 在三角形的每一个顶点处各取一个外角,这些外角的和叫做三角形的外角和.三角形的外角和等于360°判断题:1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )例2.已知:如图6.6(3),在△ABC中,AD平分外角∠EAC,∠B=∠C,求证:AD∥BC.证明:
∵∠EAC=∠B+∠C(三角形的一个外角等于和它不相邻的两个内角的和)
∠B=∠C (已知)
∴∠B= ∠EAC(等式的性质)
∵AD平分∠EAC(已知)
∴∠DAE= ∠EAC(角平分线的定义)
∴∠DAE=∠B(等量代换)
∴AD∥BC(同位角相等,两直线平行)练习1.如图,AB//CD,∠A=40°,∠D=45°,求∠1和∠2.P76—5解:∵AB//CD(已知),
∠A=40°(已知),
∴ ∠1= ∠A=40°(两直线平行,内错角相等)
∵∠D=45° (已知),
∴∠2= ∠1+ ∠D
=40°+ 45°= 85° (三角形的一个外角等于和它不相邻的两个内角的和).练习2.如图,AB//CD,∠A=45°,∠C=∠E,求∠C.P76—61解:∵AB//CD(已知),
∠A=45°(已知),
∴ ∠1= ∠A=45°(两直线平行,同位角相等)
∵ ∠C=∠E (已知),
∠1= ∠C+ ∠E
(三角形的一个外角等于和它不相邻的两个内角的和)
∴ ∠C= ∠1= 22.5° (等式的性质).3、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列练一练∠1>∠2>∠33、三角形的一个外角大于任何一个与它不相邻的内角。2、三角形的一个外角等于与它不相邻的两个内角的和;1、三角形的一个外角与它相邻的内角互补;三角形的外角与内角的关系:小结
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .1、三角形三个内角的和等于多少度?知识回顾3、在△ABC中,
∠A:∠B:∠C=2:3:4,则∠A= ,
∠B= , ∠C= . 40°60°80°65°60°创设情境,自然引入 前面我们证明了三角形内角和定理,它的证明思路是通过作辅助线,把三角形中处于不同位置的三个内角集中在一起,拼成一个平角.这样就可以证明三角形的内角和等于180°. 在证明这个定理时,先把△ABC的一边BC延长,这时在△ABC外得到∠ACD,我们把∠ACD叫做三角形ABC的外角.D 三角形的一边与另一边的延长线组成的角,叫做三角形的外角.外角的特征有三条:(1)顶点在三角形的一个顶点上. (2)一条边是三角形的一边. (3)另一条边是三角形某条边的延长线. 三角形的一个外角,就是三角形一个内角的邻补角.注意:外角不相邻内角相邻内角ABCD学一学画图并思考: 画一个△ABC ,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?归纳:每一个三角形都有6个外角. 每一个顶点相对应的外角都有2个.它们是对顶角.因此相等.每个外角与相邻的内角是邻补角. 把三角形各边向两方延长,就可以画出一个三角形所有的外角. 练习1.如图1,∠ 是△ABC的一个外角.2.图1图22.如图2,∠1是 的外角, ∠2是 的外角.3.如图3,∠BDC是 的外角, ∠EFC是______的外角, ∠BFC是________的外角图3CAE△BDC△ADC△ADC△BFC△EFC2.图中若∠A=70°,∠B=60o,试求∠ACD的度数.并说出你的理由.如果能, ∠ACD与∠A, ∠B有什么关系?1. 图中哪些角是三角形的内角,哪些角是三角形的外角?∠ACD= 130°∠ACD=∠A+ ∠B∠ACD>∠A∠ACD>∠B任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?结论:3、三角形的一个外角大于与它不相邻的任何一个内角。2、三角形的一个外角等于与它不相邻的两个内角的和;1、三角形的一个外角与它相邻的内角互补;三角形的外角与内角的关系:范例 例1、如图,∠BAE,∠CBF ,∠ACD是△ABC的三个外角,它们的和是多少? 在三角形的每一个顶点处各取一个外角,这些外角的和叫做三角形的外角和.三角形的外角和等于360°判断题:1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )例2.已知:如图6.6(3),在△ABC中,AD平分外角∠EAC,∠B=∠C,求证:AD∥BC.证明:
∵∠EAC=∠B+∠C(三角形的一个外角等于和它不相邻的两个内角的和)
∠B=∠C (已知)
∴∠B= ∠EAC(等式的性质)
∵AD平分∠EAC(已知)
∴∠DAE= ∠EAC(角平分线的定义)
∴∠DAE=∠B(等量代换)
∴AD∥BC(同位角相等,两直线平行)练习1.如图,AB//CD,∠A=40°,∠D=45°,求∠1和∠2.P76—5解:∵AB//CD(已知),
∠A=40°(已知),
∴ ∠1= ∠A=40°(两直线平行,内错角相等)
∵∠D=45° (已知),
∴∠2= ∠1+ ∠D
=40°+ 45°= 85° (三角形的一个外角等于和它不相邻的两个内角的和).练习2.如图,AB//CD,∠A=45°,∠C=∠E,求∠C.P76—61解:∵AB//CD(已知),
∠A=45°(已知),
∴ ∠1= ∠A=45°(两直线平行,同位角相等)
∵ ∠C=∠E (已知),
∠1= ∠C+ ∠E
(三角形的一个外角等于和它不相邻的两个内角的和)
∴ ∠C= ∠1= 22.5° (等式的性质).3、把图中∠1、 ∠2、 ∠3按由大到小的顺序排列练一练∠1>∠2>∠33、三角形的一个外角大于任何一个与它不相邻的内角。2、三角形的一个外角等于与它不相邻的两个内角的和;1、三角形的一个外角与它相邻的内角互补;三角形的外角与内角的关系:小结
