2.2.1直线与平面平行的判定 第一课时 课件(共19张PPT)
文档属性
| 名称 | 2.2.1直线与平面平行的判定 第一课时 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 19.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
2.2.1直线与平面平行的判定
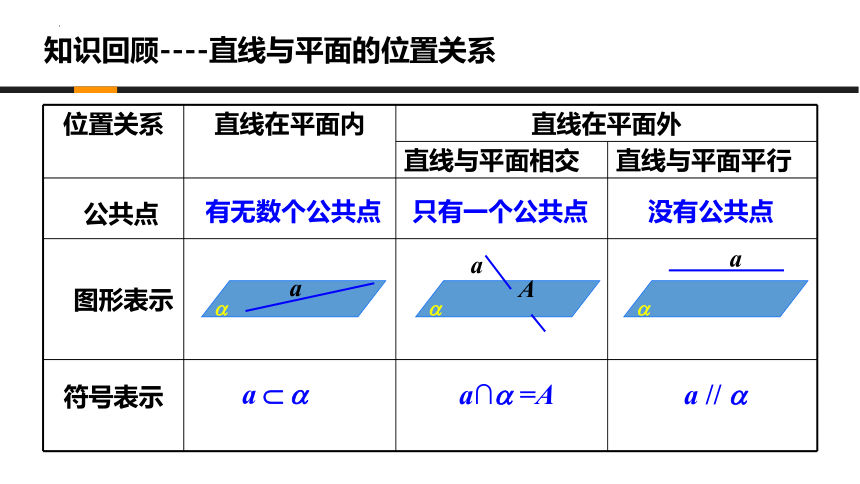
位置关系 直线在平面内 直线在平面外
直线与平面相交 直线与平面平行
公共点
有无数个公共点
只有一个公共点
没有公共点
图形表示
符号表示
a //
a∩ =A
a
a
a
a
A
知识回顾----直线与平面的位置关系
学习目标----直线与平面平行的判定
1、通过生活中的实例,抽象出几何模型,通过直观感知、操作确认,归纳出直线与平面平行的判定定理;
2、会用图形语言、文字语言、符号语言准确描述直线与平面平行的判定定理;
3、能运用直线与平面平行的判定定理证明一些简单的空间线面关系问题。
学习目标
4、体会在学习过程中蕴含的数学思想和学习几何定理的学习方法.
直观感知----直线与平面平行的判定
在这个教学楼中,哪些直线是和地面平行的
直观感知----直线与平面平行的判定
直观感知----直线与平面平行的判定
操作确认----直线与平面平行的判定
数学小实验: 实验用具:一条绳子,一把尺子。 实验要求:将绳子抻直,并保证其和地面平行。
A
B
A1
B1
你是怎么做的?请描述一下。
请同学们将此实例抽象成数学模型。并进一步思考:如何判定直线和平面平行?
操作确认----直线与平面平行的判定
直线 与平面 相交吗?
探究
不可能相交
你觉得应具备什么条件,才会使平面外的直线与平面 平行?
A
B
A1
B1
归纳总结----直线与平面平行的判定
请你试着用简洁的语言归纳出直线与平面平行的判定定理
图形语言:
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
文字语言:
符号语言:
空间问题
平面问题
降维转化
新知深化----直线与平面平行的判定
判断下列命题是否正确。
(1)
(2)
×
×
×
(3)
.
A
a
a
b
(2)
结论:证明直线与平面平行,三个条件必须具备,才能得到线面平行的结论.
α
a
b
(3)
新知运用----直线与平面平行的判定
M
N
(1)与AB平行的平面有 :
(2)过点E作出与平面 平行的线, 并证明平行关系;
例1、 正方体
中,E为棱
的中点,
新知运用----直线与平面平行的判定
例1、 正方体
中,E为棱
的中点,
(1)与AB平行的平面有 :
(2)过点E作出与平面 平行的线, 并证明平行关系;
(3)P为棱BC的中点,
证明:EP//平面
P
Q
新知运用----直线与平面平行的判定
变式
课堂小结----直线与平面平行的判定
本堂课你收获了什么?说一说
课堂小结----直线与平面平行的判定
1.证明直线与平面平行方法:
(1)利用定义;
(2)利用判定定理.
2.数学思想方法:转化的思想
空间问题
平面问题
线线平行
线面平行
要证线面平行,
只需线线平行
方法一:三角形的中位线定理;
方法三:平行四边形的平行关系。
方法二:平行线切割线段成比例定理。
方法四:平行公理
3.数学学习方法:找关键词
达标检测----直线与平面平行的判定
A.若 //平面 ,则 平行于 内的任何直线;
C.若 与平面 内的无数条直线平行,则 //平面 ;
B.若直线 在平面 外,则 //平面 ;
D.若直线 ∥b,b ,那么直线 就平行于平面 内
的无数条直线
1.下列说法正确的是( )
D
达标检测----直线与平面平行的判定
2.如图,P是平行四边形ABCD所在平面外一点,E为PB中点,O为AC、 BD的交点,则图中与EO平行的平面有 .
平面PDA,平面PDC
达标检测----直线与平面平行的判定
3.如图,在四棱锥P-ABCD中,ABCD是平行四边形, M、N分别是AB、PC的中点.
求证:MN//平面PAD
E
本节内容结束!再见
2.2.1直线与平面平行的判定
位置关系 直线在平面内 直线在平面外
直线与平面相交 直线与平面平行
公共点
有无数个公共点
只有一个公共点
没有公共点
图形表示
符号表示
a //
a∩ =A
a
a
a
a
A
知识回顾----直线与平面的位置关系
学习目标----直线与平面平行的判定
1、通过生活中的实例,抽象出几何模型,通过直观感知、操作确认,归纳出直线与平面平行的判定定理;
2、会用图形语言、文字语言、符号语言准确描述直线与平面平行的判定定理;
3、能运用直线与平面平行的判定定理证明一些简单的空间线面关系问题。
学习目标
4、体会在学习过程中蕴含的数学思想和学习几何定理的学习方法.
直观感知----直线与平面平行的判定
在这个教学楼中,哪些直线是和地面平行的
直观感知----直线与平面平行的判定
直观感知----直线与平面平行的判定
操作确认----直线与平面平行的判定
数学小实验: 实验用具:一条绳子,一把尺子。 实验要求:将绳子抻直,并保证其和地面平行。
A
B
A1
B1
你是怎么做的?请描述一下。
请同学们将此实例抽象成数学模型。并进一步思考:如何判定直线和平面平行?
操作确认----直线与平面平行的判定
直线 与平面 相交吗?
探究
不可能相交
你觉得应具备什么条件,才会使平面外的直线与平面 平行?
A
B
A1
B1
归纳总结----直线与平面平行的判定
请你试着用简洁的语言归纳出直线与平面平行的判定定理
图形语言:
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
文字语言:
符号语言:
空间问题
平面问题
降维转化
新知深化----直线与平面平行的判定
判断下列命题是否正确。
(1)
(2)
×
×
×
(3)
.
A
a
a
b
(2)
结论:证明直线与平面平行,三个条件必须具备,才能得到线面平行的结论.
α
a
b
(3)
新知运用----直线与平面平行的判定
M
N
(1)与AB平行的平面有 :
(2)过点E作出与平面 平行的线, 并证明平行关系;
例1、 正方体
中,E为棱
的中点,
新知运用----直线与平面平行的判定
例1、 正方体
中,E为棱
的中点,
(1)与AB平行的平面有 :
(2)过点E作出与平面 平行的线, 并证明平行关系;
(3)P为棱BC的中点,
证明:EP//平面
P
Q
新知运用----直线与平面平行的判定
变式
课堂小结----直线与平面平行的判定
本堂课你收获了什么?说一说
课堂小结----直线与平面平行的判定
1.证明直线与平面平行方法:
(1)利用定义;
(2)利用判定定理.
2.数学思想方法:转化的思想
空间问题
平面问题
线线平行
线面平行
要证线面平行,
只需线线平行
方法一:三角形的中位线定理;
方法三:平行四边形的平行关系。
方法二:平行线切割线段成比例定理。
方法四:平行公理
3.数学学习方法:找关键词
达标检测----直线与平面平行的判定
A.若 //平面 ,则 平行于 内的任何直线;
C.若 与平面 内的无数条直线平行,则 //平面 ;
B.若直线 在平面 外,则 //平面 ;
D.若直线 ∥b,b ,那么直线 就平行于平面 内
的无数条直线
1.下列说法正确的是( )
D
达标检测----直线与平面平行的判定
2.如图,P是平行四边形ABCD所在平面外一点,E为PB中点,O为AC、 BD的交点,则图中与EO平行的平面有 .
平面PDA,平面PDC
达标检测----直线与平面平行的判定
3.如图,在四棱锥P-ABCD中,ABCD是平行四边形, M、N分别是AB、PC的中点.
求证:MN//平面PAD
E
本节内容结束!再见
