第十二章全等三角形章节训练(含答案)2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 第十二章全等三角形章节训练(含答案)2023-2024学年人教版数学八年级上册 | 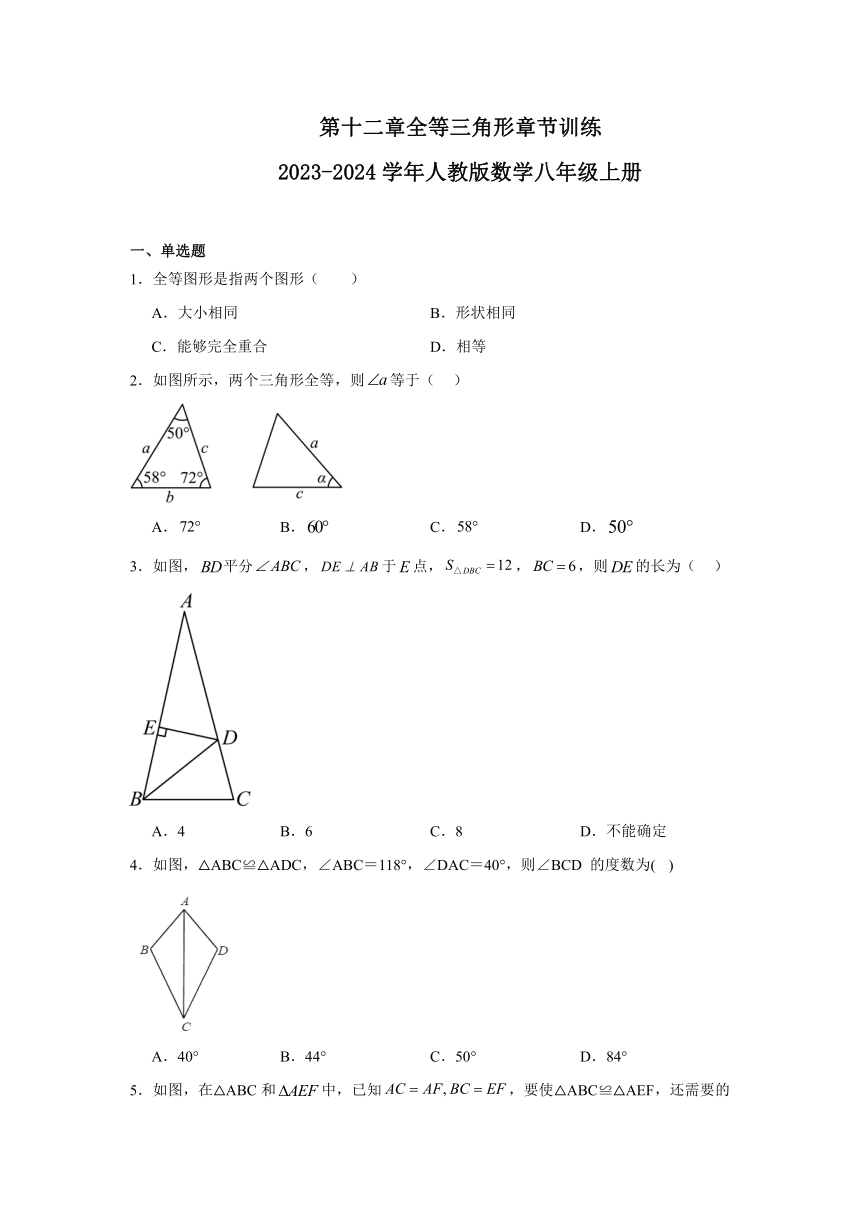 | |
| 格式 | docx | ||
| 文件大小 | 570.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 13:32:17 | ||
图片预览




文档简介
第十二章全等三角形章节训练
2023-2024学年人教版数学八年级上册
一、单选题
1.全等图形是指两个图形( )
A.大小相同 B.形状相同
C.能够完全重合 D.相等
2.如图所示,两个三角形全等,则等于( )
A. B. C. D.
3.如图,平分,于点,,,则的长为( )
A.4 B.6 C.8 D.不能确定
4.如图,△ABC≌△ADC,∠ABC=118°,∠DAC=40°,则∠BCD 的度数为( )
A.40° B.44° C.50° D.84°
5.如图,在△ABC和中,已知,要使△ABC≌△AEF,还需要的条件是( )
A. B.
C. D.
6.如图,在中,,,平分交于点,,垂足为,且,则的周长是( )
A. B. C. D.
7.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
A.① B.② C.③ D.①和②
8.如图,为测量池塘两侧A,B两点间距离,在地面上找一点C,连接,,使,然后在的延长线上确定点D,使,得到,通过测量的长,就能得出的长.那么的理由是( )
A. B. C. D.
9.如图,△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,连CD,下列结论:①AB-AC=CE;②∠CDB=135°;③S△ACE=2 S△CDB;④AB=3CD,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
11.如图为了测量B点到河对而的目标A之间的距离,在B点同侧选择了一点C,测得,,然后在M处立了标杆,使,,得到,所以测得的长就是A,B两点间的距离,这里判定的理由是( )
A. B. C. D.
二、填空题
12.如图,已知∠ABC=∠ABD,要使△ABC≌△ABD,请添加一个条件 .(不添加辅助线,只需写出一个条件即可)
13.如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=52°,则∠AEB= .
14.如图,在△ABC,△ADE中,,,,C,D,E三点在同一直线上,连接,以下四个结论
①;②;
③;④.
其中结论正确的是 .(把正确结论的序号填在横线上).
15.在如图所示的3×3正方形网格中, 度.
16.已知△ABC≌△DEF,△ABC的周长为12,则△DEF的周长为
17.如图,,,M、N分别是、的中点,若的面积为,则图中阴影部分的面积为 .
三、解答题
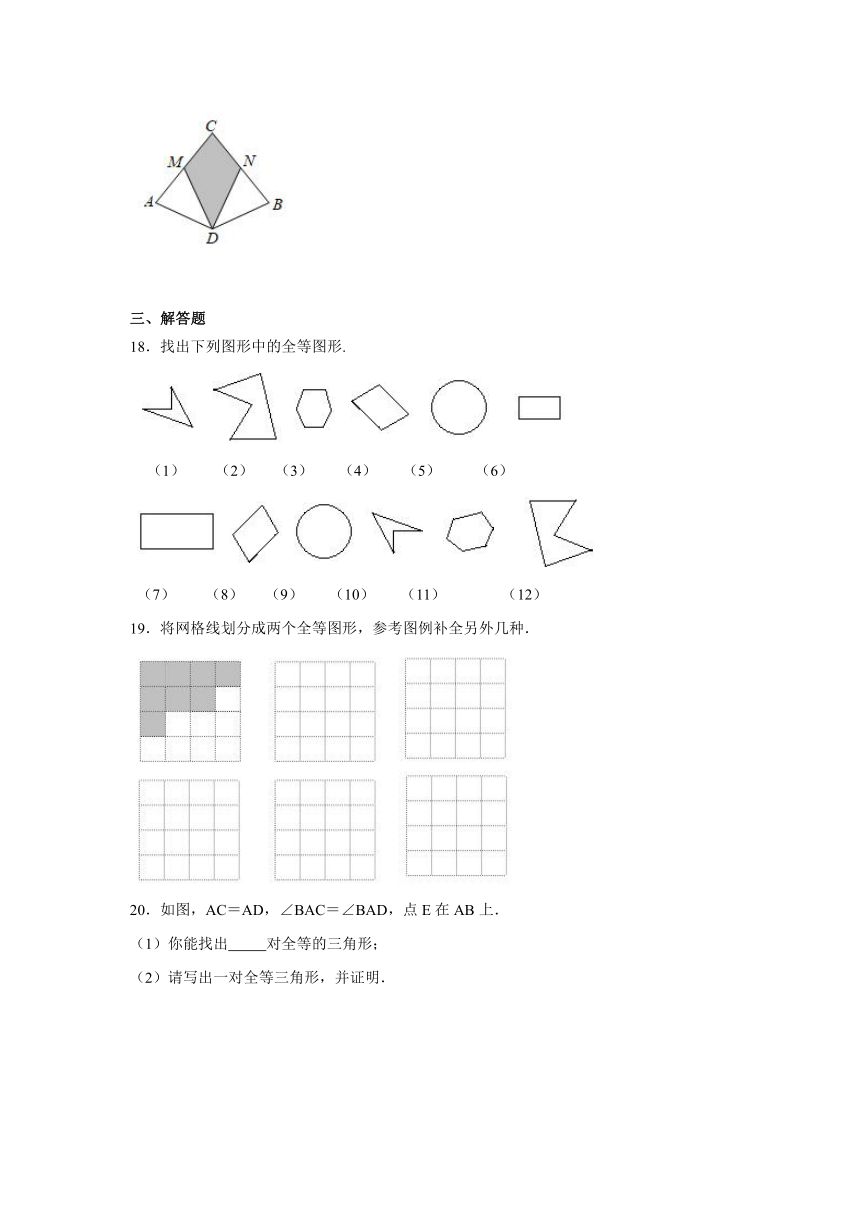
18.找出下列图形中的全等图形.
(1) (2) (3) (4) (5) (6)
(7) (8) (9) (10) (11) (12)
19.将网格线划分成两个全等图形,参考图例补全另外几种.
20.如图,AC=AD,∠BAC=∠BAD,点E在AB上.
(1)你能找出 对全等的三角形;
(2)请写出一对全等三角形,并证明.
21.如图,,点、在线段上,,.求证:.
22.如图,OC平分∠AOB,CD⊥OA,交OA于点D,CE⊥OB,交OB于点E,M,N分别在OA,OB上,且OM=ON.
求证:△CDM≌△CEN.
23.如图,点E是的中点,,平分.求证:
(1)平分;
(2).
24.已知:,,.
(1)如图1当点在上,______.
(2)如图2猜想△BDC与△ACE的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)
25.如图所示,在△ABC中:
(1)下列操作中,作的平分线的正确顺序是_________(将序号按正确的顺序写在横线上).
①分别以点,为圆心,大于的长为半径画弧,在内,两弧交于点.
②以点为圆心,适当长为半径画弧,交于点,交于点.
③画射线,交于点D.
(2)能说明的依据是_________(填序号).
①. ②. ③. ④角平分线上的点到角两边的距离相等.
(3)若S△ABC=90,过点作于点,求的长.
参考答案:
1.C
2.D
3.A
4.B
5.B
6.D
7.C
8.A
9.B
10.C
11.C
12.BC=BD.
13.142°
14.①③④
15.
16.12
17.3
18.(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形
19.如图所示,(答案不唯一)
20.本题要判全等三角形,已知AC=AD,∠BAC=∠BAD,点E在AB上.具备了一组边对应相等,一组对应角相等,可分别根据SSS、SAS、AAS,ASA能判定有几对全等三角形.
21.根据,得出,再利用证明直角三角形全等,即可得出结论.
22.证明:∵OC平分∠AOC,
∴∠DOC=∠EOC,
在△OMC和△ONC中,
∵OM=ON,∠DOC=∠EOC,OC=OC
∴△OMC≌△ONC(SAS),
∴MC=NC,
∵OC平分∠AOC,CD⊥OA,CE⊥OB,
∴CD=CE,
在Rt△DMC和Rt△ENC中
∵DC=CE,CM=CN,
∴Rt△DMC≌Rt△ENC(HL).
23.(1)证明:如下图,过E作于F,
∵,平分,
∴,
∵点E是的中点,
∴,
∴,
∵,
∴,
在Rt△EFD和Rt△ECD中
,
∴Rt△EFD≌Rt△ECD(HL)
∴,
∴平分;
(2)解:由(1)知Rt△EFD≌Rt△ECD
∴,
在Rt△AEF和Rt△AEB中
,
∴Rt△AEF≌Rt△AEB(HL)
∴,
∵,
∴.
24.(1)
(2) S△BDC=S△ACE
25.(1)②①③
(2)①
(3)
2023-2024学年人教版数学八年级上册
一、单选题
1.全等图形是指两个图形( )
A.大小相同 B.形状相同
C.能够完全重合 D.相等
2.如图所示,两个三角形全等,则等于( )
A. B. C. D.
3.如图,平分,于点,,,则的长为( )
A.4 B.6 C.8 D.不能确定
4.如图,△ABC≌△ADC,∠ABC=118°,∠DAC=40°,则∠BCD 的度数为( )
A.40° B.44° C.50° D.84°
5.如图,在△ABC和中,已知,要使△ABC≌△AEF,还需要的条件是( )
A. B.
C. D.
6.如图,在中,,,平分交于点,,垂足为,且,则的周长是( )
A. B. C. D.
7.小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
A.① B.② C.③ D.①和②
8.如图,为测量池塘两侧A,B两点间距离,在地面上找一点C,连接,,使,然后在的延长线上确定点D,使,得到,通过测量的长,就能得出的长.那么的理由是( )
A. B. C. D.
9.如图,△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于D,连CD,下列结论:①AB-AC=CE;②∠CDB=135°;③S△ACE=2 S△CDB;④AB=3CD,其中正确的有( )
A.4个 B.3个 C.2个 D.1个
10.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角∠ACB与∠DEF的度数和为( )
A.60° B.75° C.90° D.120°
11.如图为了测量B点到河对而的目标A之间的距离,在B点同侧选择了一点C,测得,,然后在M处立了标杆,使,,得到,所以测得的长就是A,B两点间的距离,这里判定的理由是( )
A. B. C. D.
二、填空题
12.如图,已知∠ABC=∠ABD,要使△ABC≌△ABD,请添加一个条件 .(不添加辅助线,只需写出一个条件即可)
13.如图,AC=BC,DC=EC,∠ACB=∠ECD=90°,且∠EBD=52°,则∠AEB= .
14.如图,在△ABC,△ADE中,,,,C,D,E三点在同一直线上,连接,以下四个结论
①;②;
③;④.
其中结论正确的是 .(把正确结论的序号填在横线上).
15.在如图所示的3×3正方形网格中, 度.
16.已知△ABC≌△DEF,△ABC的周长为12,则△DEF的周长为
17.如图,,,M、N分别是、的中点,若的面积为,则图中阴影部分的面积为 .
三、解答题
18.找出下列图形中的全等图形.
(1) (2) (3) (4) (5) (6)
(7) (8) (9) (10) (11) (12)
19.将网格线划分成两个全等图形,参考图例补全另外几种.
20.如图,AC=AD,∠BAC=∠BAD,点E在AB上.
(1)你能找出 对全等的三角形;
(2)请写出一对全等三角形,并证明.
21.如图,,点、在线段上,,.求证:.
22.如图,OC平分∠AOB,CD⊥OA,交OA于点D,CE⊥OB,交OB于点E,M,N分别在OA,OB上,且OM=ON.
求证:△CDM≌△CEN.
23.如图,点E是的中点,,平分.求证:
(1)平分;
(2).
24.已知:,,.
(1)如图1当点在上,______.
(2)如图2猜想△BDC与△ACE的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)
25.如图所示,在△ABC中:
(1)下列操作中,作的平分线的正确顺序是_________(将序号按正确的顺序写在横线上).
①分别以点,为圆心,大于的长为半径画弧,在内,两弧交于点.
②以点为圆心,适当长为半径画弧,交于点,交于点.
③画射线,交于点D.
(2)能说明的依据是_________(填序号).
①. ②. ③. ④角平分线上的点到角两边的距离相等.
(3)若S△ABC=90,过点作于点,求的长.
参考答案:
1.C
2.D
3.A
4.B
5.B
6.D
7.C
8.A
9.B
10.C
11.C
12.BC=BD.
13.142°
14.①③④
15.
16.12
17.3
18.(1)和(10),(2)和(12),(4)和(8),(5)和(9)是全等图形
19.如图所示,(答案不唯一)
20.本题要判全等三角形,已知AC=AD,∠BAC=∠BAD,点E在AB上.具备了一组边对应相等,一组对应角相等,可分别根据SSS、SAS、AAS,ASA能判定有几对全等三角形.
21.根据,得出,再利用证明直角三角形全等,即可得出结论.
22.证明:∵OC平分∠AOC,
∴∠DOC=∠EOC,
在△OMC和△ONC中,
∵OM=ON,∠DOC=∠EOC,OC=OC
∴△OMC≌△ONC(SAS),
∴MC=NC,
∵OC平分∠AOC,CD⊥OA,CE⊥OB,
∴CD=CE,
在Rt△DMC和Rt△ENC中
∵DC=CE,CM=CN,
∴Rt△DMC≌Rt△ENC(HL).
23.(1)证明:如下图,过E作于F,
∵,平分,
∴,
∵点E是的中点,
∴,
∴,
∵,
∴,
在Rt△EFD和Rt△ECD中
,
∴Rt△EFD≌Rt△ECD(HL)
∴,
∴平分;
(2)解:由(1)知Rt△EFD≌Rt△ECD
∴,
在Rt△AEF和Rt△AEB中
,
∴Rt△AEF≌Rt△AEB(HL)
∴,
∵,
∴.
24.(1)
(2) S△BDC=S△ACE
25.(1)②①③
(2)①
(3)
