四川省成都市蓉城名校联盟2023-2024学年高二上学期期中联考数学试题(含解析)
文档属性
| 名称 | 四川省成都市蓉城名校联盟2023-2024学年高二上学期期中联考数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 773.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-04 00:00:00 | ||
图片预览




文档简介
成都市蓉城名校联盟2023-2024学年高二上学期期中联考
数学
考试时间120分钟,满分150分
注意事项:
1.答题前,考生务必在答题卡上将自己的姓名、座位号、准考证号用0.5毫米的黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“贴条形码区”。
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米的黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.袋中装有4个大小、质地完全相同的带有不同标号的小球,其中2个红球,2个绿球,甲摸一个后不放回,乙再摸一个,试验所有可能的结果数为( )
A.8 B.9 C.12 D.16
2.某大型联考有16000名学生参加,已知所有学生成绩的第60百分位数是515分,则成绩在515分以上的人数至少有( )
A.6000人 B.6240人 C.6300人 D.6400人
3.给出下列命题:
①若空间向量,满足,则与的夹角为钝角;
②空间任意两个单位向量必相等;
③对于非零向量,若,则;
④若为空间的一个基底,则构成空间的另一个基底.其中说法正确的个数为( )
A.0 B.1 C.2 D.3
4.某地高校有100人参加2023数学建模竞赛,成绩频数分布表如下,根据该表估计该校大学生数学建模竞赛成绩的平均分为( )
成绩分组/分
人数/人 4 25 50 15 6
A.59 B.59.4 C.69 D.69.4
5.若,则事件与的关系为( )
A.相互独立 B.互为对立 C.互斥 D.无法判断
6.把边长为的正方形沿对角线折起,使得平面与平面所成二面角的大小为,则异面直线与所成角的余弦值为( )
A. B. C. D.
7.某校2023年秋季入学考试,某班数学平均分为125分,方差为.成绩分析时发现有三名同学的成绩录入有误,同学实际成绩137分,被错录为118分;同学实际成绩115分,被错录为103分;同学实际成绩98分,被错录为129分,更正后重新统计,得到方差为,则与的大小关系为( )
A. B. C. D.不能确定
8.如图所示的多面体是由底面为的长方体被截面所截得到的,其中,则中点到平面的距离为( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求;全部选对的得5分,选对但不全的得2分,有选错的得0分。
9.一组数据的平均数为,方差为,新数据的平均值为,方差为.下列结论正确的是( )
A. B. C. D.
10.下面结论正确的是( )
A.若事件与相互独立,则与也相互独立
B.若事件与是互斥事件,则与也是互斥事件
C.若与相互独立,则
D.若,则与互为对立事件
11.某单位健康体测,男性平均体重为64千克,方差为151;女性平均体重为56千克,方差为159,男女人数之比为,该单位全体工作人员平均体重和方差分别为( )
A. B. C. D.
12.如图,在四棱锥中,底面是正方形,底面,点是中点,点是棱上的动点(与端点不重合).下列说法正确的是( )
A.从六个点中任取三点恰能确定一个平面的概率为
B.从六个点中任取四点恰能构成三棱锥的概率为
C.存在点,使直线与所成的角为
D.不存在点,使平面
三、填空题:本题共4小题,每小题5分,共20分。
13.某射击运动员每次击中靶心的概率均为0.6.现采用随机模拟的方法估计该运动员射击4次至少击中2次的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1,2,3表示没有击中靶心,4,5,6,7,8,9表示击中靶心;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
8636 0293 7140 9857 5727 0347 4373 9647 4698 3312
6710 0371 6233 2616 9597 8045 6011 3661 4281 7424
据此估计,该射击运动员射击4次至少击中2次靶心的概率为________.
14.某区从11000名小学生、10000名初中生和4000名高中生中采用分层抽样方法抽取n名学生进行视力测试,若初中生比高中生多抽取60人,则________.
15.某高中的独孤与无极两支排球队在校运会中采用五局三胜制(有球队先胜三局则比赛结束).第一局独孤队获胜概率为0.4,独孤队发挥受情绪影响较大,若前一局获胜,下一局获胜概率增加0.1,反之降低0.1.则独孤队不超过四局获胜的概率为________.
16.已知空间向量两两之间的夹角均为,且,若向量分别满足与,则的最小值为________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
某稻谷试验田试种了两个品种的水稻各10亩,并在稻谷成熟后统计了这20亩地的稻谷产量如下表,记两个品种各10亩产量的平均数分别为和,方差分别为和.
(单位:) 60 63 50 76 71 85 75 63 63 64
(单位:) 56 62 60 68 78 75 76 62 63 70
(1)分别求这两个品种产量的极差和中位数;
(2)求;
(3)依据以上计算结果进行分析,推广种植品种还是品种水稻更合适.
18.(12分)
如图,在四棱锥中,底面为正方形,底面,,点为的中点,点在线段上且.
(1)用向量表示向量;
(2)求的长.
19.(12分)
药品监督局检测某种产品的两个质量指标,用综合指标核定该产品的等级.若,则核定该产品为一等品.现从一批该产品中随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
质量指标
产品编号
质量指标
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取2件产品,设事件为“在抽取的2件产品中,每件产品的综合指标均满足”,求事件的概率.
20.(12分)
如图四边形是平行四边形,,四边形是梯形,,且,沿将四边形翻折后使得平面平面.
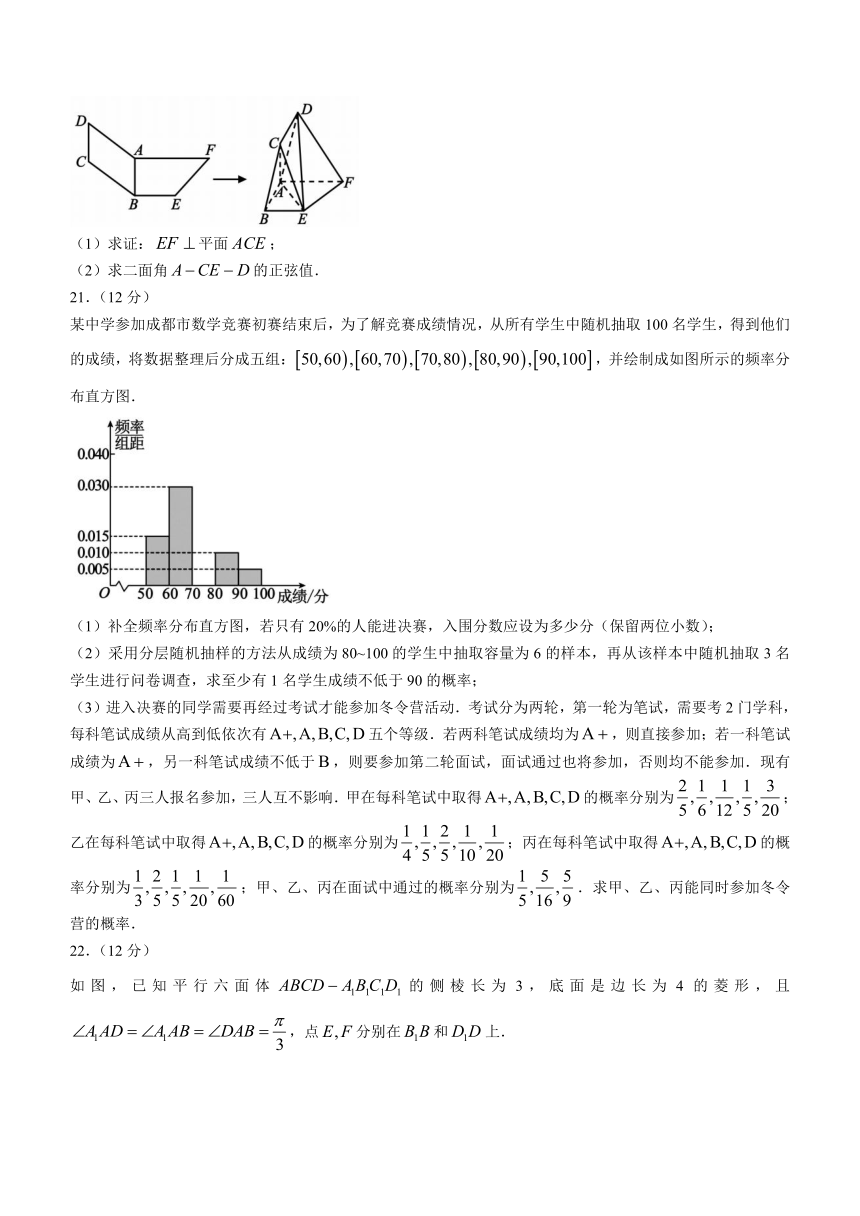
(1)求证:平面;
(2)求二面角的正弦值.
21.(12分)
某中学参加成都市数学竞赛初赛结束后,为了解竞赛成绩情况,从所有学生中随机抽取100名学生,得到他们的成绩,将数据整理后分成五组:,并绘制成如图所示的频率分布直方图.
(1)补全频率分布直方图,若只有20%的人能进决赛,入围分数应设为多少分(保留两位小数);
(2)采用分层随机抽样的方法从成绩为80~100的学生中抽取容量为6的样本,再从该样本中随机抽取3名学生进行问卷调查,求至少有1名学生成绩不低于90的概率;
(3)进入决赛的同学需要再经过考试才能参加冬令营活动.考试分为两轮,第一轮为笔试,需要考2门学科,每科笔试成绩从高到低依次有五个等级.若两科笔试成绩均为,则直接参加;若一科笔试成绩为,另一科笔试成绩不低于,则要参加第二轮面试,面试通过也将参加,否则均不能参加.现有甲、乙、丙三人报名参加,三人互不影响.甲在每科笔试中取得的概率分别为;乙在每科笔试中取得的概率分别为;丙在每科笔试中取得的概率分别为;甲、乙、丙在面试中通过的概率分别为.求甲、乙、丙能同时参加冬令营的概率.
22.(12分)
如图,已知平行六面体的侧棱长为3,底面是边长为4的菱形,且,点分别在和上.
(1)若,求证:四点共面;
(2)求;
(3)若,点为线段上(包括端点)的动点,求直线与平面所成角的正弦值的取值范围.
成都市蓉城名校联盟2023-2024学年高二上学期期中联考
数学参考答案及评分标准
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1 2 3 4 5 6 7 8
C D B D A D C D
1.解:设4个小球分别为,则试验结果为.
2.解:.
4.解:.
5.解:,得,
又.
6解:取中点,连接,以分别为轴建立空间直角坐标系,则,,用余弦定理可求出结果为.
7.解:设班级人数为,因为,所以更正前后平均分不变,且,所以.
8.解:以为原点,分别以所在直线为轴,轴,轴建立空间直角坐标系,则,,
设为平面的法向量,,
由,得,令
所以,又,
点到平面的距离为.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求;全部选对的得5分,选对但不全的得2分,有选错的得0分。
9 10 11 12
CD AC AD ABC
9.解:方差只与系数有关.
11.解:依题意,设男性人数为,女性人数为,该单位全体人员体重的平均数为:
,
所以该单位全体人员体重的方差为:.
12.解:任取3点,有20个样本点,除开和分别共线,其余18种均不共线,故概率为;任取4点,共有15个样本点;每条直线上任取2个点,则共有9个样本点,故概率为.故A、B正确.
以为空间原点建立空间直角坐标系,设,则,,解得,方程有解,故C正确.
设平面的法向量,由,可得,故D错误.
三、填空题:本题共4小题,每小题5分,共20分。
13. 14.250 15.0.236 16.
13.解:恰好0次击中包含3321一个样本点,恰好1次击中包含6233,0293,0371,6011四个样本点,故至多击中一次包含五个样本点,对立事件至少2次击中则包含15个样本点,故概率为.
14.解:,解得,从而求出.
15.解:由题意,甲取胜的可能结果为四个互斥事件:,
.
16.解:,
因为,所以,
,所以,
令,则,且,
由,得,所以,
所以,当且仅当共线时等号成立,故答案为.
几何法:令,设,令,则;
令,则,过点作平面,使得;
过点作平面,使得;
,即点在平面上;,即点在平面上;
由,即点在以点为球心的球面上;
故,此时三点共线,且,
即共线.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
解:(1)由题意可知,极差:产品为35,产品为22,
中位数:产品为63.5,产品为65.5;
(2)由题意:,
,
;
(3)结合第(2)问可知两个品种水稻的产量平均数一样,但是的方差较小,较稳定,所以推广品种水稻更合适.
18.(12分)
解:(1);
(2),
,
.
19.(12分)
解:(1)一等品率为0.6;
(2),
.
20.(12分)
解:(1),
,连接,
,
平面平面,平面平面,
平面,
平面;
(2)以为原点建立空间直角坐标系,,
,
设平面和平面的法向量分别为,
,取,
,取,
,
,即二面角的正弦值为.
21.(12分)
解:(1)的频率为,
;
(2)抽取4人,抽取2人,设事件:“至少有1名学生成绩不低于90”,
;
(3),
,
,
所以.
22.(12分)
解:(1),
,所以四点共面;
(2)平面,
上的所有的点到平面的距离都相等,同理上所有的点到的距离也相等,
,
,
点在平面的射影落在上,过点作,过点作,
底面是边长为4的菱形,侧棱长为3,,
;
(3)建立如图所示空间直角坐标系,由(2)可知,
,
,
设为平面的法向量,,
取,
,
,,
,
.
数学
考试时间120分钟,满分150分
注意事项:
1.答题前,考生务必在答题卡上将自己的姓名、座位号、准考证号用0.5毫米的黑色签字笔填写清楚,考生考试条形码由监考老师粘贴在答题卡上的“贴条形码区”。
2.选择题使用2B铅笔填涂在答题卡上对应题目标号的位置上,如需改动,用橡皮擦擦干净后再填涂其它答案;非选择题用0.5毫米的黑色签字笔在答题卡的对应区域内作答,超出答题区域答题的答案无效;在草稿纸上、试卷上答题无效。
3.考试结束后由监考老师将答题卡收回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.袋中装有4个大小、质地完全相同的带有不同标号的小球,其中2个红球,2个绿球,甲摸一个后不放回,乙再摸一个,试验所有可能的结果数为( )
A.8 B.9 C.12 D.16
2.某大型联考有16000名学生参加,已知所有学生成绩的第60百分位数是515分,则成绩在515分以上的人数至少有( )
A.6000人 B.6240人 C.6300人 D.6400人
3.给出下列命题:
①若空间向量,满足,则与的夹角为钝角;
②空间任意两个单位向量必相等;
③对于非零向量,若,则;
④若为空间的一个基底,则构成空间的另一个基底.其中说法正确的个数为( )
A.0 B.1 C.2 D.3
4.某地高校有100人参加2023数学建模竞赛,成绩频数分布表如下,根据该表估计该校大学生数学建模竞赛成绩的平均分为( )
成绩分组/分
人数/人 4 25 50 15 6
A.59 B.59.4 C.69 D.69.4
5.若,则事件与的关系为( )
A.相互独立 B.互为对立 C.互斥 D.无法判断
6.把边长为的正方形沿对角线折起,使得平面与平面所成二面角的大小为,则异面直线与所成角的余弦值为( )
A. B. C. D.
7.某校2023年秋季入学考试,某班数学平均分为125分,方差为.成绩分析时发现有三名同学的成绩录入有误,同学实际成绩137分,被错录为118分;同学实际成绩115分,被错录为103分;同学实际成绩98分,被错录为129分,更正后重新统计,得到方差为,则与的大小关系为( )
A. B. C. D.不能确定
8.如图所示的多面体是由底面为的长方体被截面所截得到的,其中,则中点到平面的距离为( )
A. B. C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求;全部选对的得5分,选对但不全的得2分,有选错的得0分。
9.一组数据的平均数为,方差为,新数据的平均值为,方差为.下列结论正确的是( )
A. B. C. D.
10.下面结论正确的是( )
A.若事件与相互独立,则与也相互独立
B.若事件与是互斥事件,则与也是互斥事件
C.若与相互独立,则
D.若,则与互为对立事件
11.某单位健康体测,男性平均体重为64千克,方差为151;女性平均体重为56千克,方差为159,男女人数之比为,该单位全体工作人员平均体重和方差分别为( )
A. B. C. D.
12.如图,在四棱锥中,底面是正方形,底面,点是中点,点是棱上的动点(与端点不重合).下列说法正确的是( )
A.从六个点中任取三点恰能确定一个平面的概率为
B.从六个点中任取四点恰能构成三棱锥的概率为
C.存在点,使直线与所成的角为
D.不存在点,使平面
三、填空题:本题共4小题,每小题5分,共20分。
13.某射击运动员每次击中靶心的概率均为0.6.现采用随机模拟的方法估计该运动员射击4次至少击中2次的概率:先由计算器算出0到9之间取整数值的随机数,指定0,1,2,3表示没有击中靶心,4,5,6,7,8,9表示击中靶心;因为射击4次,故以每4个随机数为一组,代表射击4次的结果.经随机模拟产生了20组随机数:
8636 0293 7140 9857 5727 0347 4373 9647 4698 3312
6710 0371 6233 2616 9597 8045 6011 3661 4281 7424
据此估计,该射击运动员射击4次至少击中2次靶心的概率为________.
14.某区从11000名小学生、10000名初中生和4000名高中生中采用分层抽样方法抽取n名学生进行视力测试,若初中生比高中生多抽取60人,则________.
15.某高中的独孤与无极两支排球队在校运会中采用五局三胜制(有球队先胜三局则比赛结束).第一局独孤队获胜概率为0.4,独孤队发挥受情绪影响较大,若前一局获胜,下一局获胜概率增加0.1,反之降低0.1.则独孤队不超过四局获胜的概率为________.
16.已知空间向量两两之间的夹角均为,且,若向量分别满足与,则的最小值为________.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
某稻谷试验田试种了两个品种的水稻各10亩,并在稻谷成熟后统计了这20亩地的稻谷产量如下表,记两个品种各10亩产量的平均数分别为和,方差分别为和.
(单位:) 60 63 50 76 71 85 75 63 63 64
(单位:) 56 62 60 68 78 75 76 62 63 70
(1)分别求这两个品种产量的极差和中位数;
(2)求;
(3)依据以上计算结果进行分析,推广种植品种还是品种水稻更合适.
18.(12分)
如图,在四棱锥中,底面为正方形,底面,,点为的中点,点在线段上且.
(1)用向量表示向量;
(2)求的长.
19.(12分)
药品监督局检测某种产品的两个质量指标,用综合指标核定该产品的等级.若,则核定该产品为一等品.现从一批该产品中随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
质量指标
产品编号
质量指标
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品的一等品中,随机抽取2件产品,设事件为“在抽取的2件产品中,每件产品的综合指标均满足”,求事件的概率.
20.(12分)
如图四边形是平行四边形,,四边形是梯形,,且,沿将四边形翻折后使得平面平面.
(1)求证:平面;
(2)求二面角的正弦值.
21.(12分)
某中学参加成都市数学竞赛初赛结束后,为了解竞赛成绩情况,从所有学生中随机抽取100名学生,得到他们的成绩,将数据整理后分成五组:,并绘制成如图所示的频率分布直方图.
(1)补全频率分布直方图,若只有20%的人能进决赛,入围分数应设为多少分(保留两位小数);
(2)采用分层随机抽样的方法从成绩为80~100的学生中抽取容量为6的样本,再从该样本中随机抽取3名学生进行问卷调查,求至少有1名学生成绩不低于90的概率;
(3)进入决赛的同学需要再经过考试才能参加冬令营活动.考试分为两轮,第一轮为笔试,需要考2门学科,每科笔试成绩从高到低依次有五个等级.若两科笔试成绩均为,则直接参加;若一科笔试成绩为,另一科笔试成绩不低于,则要参加第二轮面试,面试通过也将参加,否则均不能参加.现有甲、乙、丙三人报名参加,三人互不影响.甲在每科笔试中取得的概率分别为;乙在每科笔试中取得的概率分别为;丙在每科笔试中取得的概率分别为;甲、乙、丙在面试中通过的概率分别为.求甲、乙、丙能同时参加冬令营的概率.
22.(12分)
如图,已知平行六面体的侧棱长为3,底面是边长为4的菱形,且,点分别在和上.
(1)若,求证:四点共面;
(2)求;
(3)若,点为线段上(包括端点)的动点,求直线与平面所成角的正弦值的取值范围.
成都市蓉城名校联盟2023-2024学年高二上学期期中联考
数学参考答案及评分标准
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1 2 3 4 5 6 7 8
C D B D A D C D
1.解:设4个小球分别为,则试验结果为.
2.解:.
4.解:.
5.解:,得,
又.
6解:取中点,连接,以分别为轴建立空间直角坐标系,则,,用余弦定理可求出结果为.
7.解:设班级人数为,因为,所以更正前后平均分不变,且,所以.
8.解:以为原点,分别以所在直线为轴,轴,轴建立空间直角坐标系,则,,
设为平面的法向量,,
由,得,令
所以,又,
点到平面的距离为.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求;全部选对的得5分,选对但不全的得2分,有选错的得0分。
9 10 11 12
CD AC AD ABC
9.解:方差只与系数有关.
11.解:依题意,设男性人数为,女性人数为,该单位全体人员体重的平均数为:
,
所以该单位全体人员体重的方差为:.
12.解:任取3点,有20个样本点,除开和分别共线,其余18种均不共线,故概率为;任取4点,共有15个样本点;每条直线上任取2个点,则共有9个样本点,故概率为.故A、B正确.
以为空间原点建立空间直角坐标系,设,则,,解得,方程有解,故C正确.
设平面的法向量,由,可得,故D错误.
三、填空题:本题共4小题,每小题5分,共20分。
13. 14.250 15.0.236 16.
13.解:恰好0次击中包含3321一个样本点,恰好1次击中包含6233,0293,0371,6011四个样本点,故至多击中一次包含五个样本点,对立事件至少2次击中则包含15个样本点,故概率为.
14.解:,解得,从而求出.
15.解:由题意,甲取胜的可能结果为四个互斥事件:,
.
16.解:,
因为,所以,
,所以,
令,则,且,
由,得,所以,
所以,当且仅当共线时等号成立,故答案为.
几何法:令,设,令,则;
令,则,过点作平面,使得;
过点作平面,使得;
,即点在平面上;,即点在平面上;
由,即点在以点为球心的球面上;
故,此时三点共线,且,
即共线.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
解:(1)由题意可知,极差:产品为35,产品为22,
中位数:产品为63.5,产品为65.5;
(2)由题意:,
,
;
(3)结合第(2)问可知两个品种水稻的产量平均数一样,但是的方差较小,较稳定,所以推广品种水稻更合适.
18.(12分)
解:(1);
(2),
,
.
19.(12分)
解:(1)一等品率为0.6;
(2),
.
20.(12分)
解:(1),
,连接,
,
平面平面,平面平面,
平面,
平面;
(2)以为原点建立空间直角坐标系,,
,
设平面和平面的法向量分别为,
,取,
,取,
,
,即二面角的正弦值为.
21.(12分)
解:(1)的频率为,
;
(2)抽取4人,抽取2人,设事件:“至少有1名学生成绩不低于90”,
;
(3),
,
,
所以.
22.(12分)
解:(1),
,所以四点共面;
(2)平面,
上的所有的点到平面的距离都相等,同理上所有的点到的距离也相等,
,
,
点在平面的射影落在上,过点作,过点作,
底面是边长为4的菱形,侧棱长为3,,
;
(3)建立如图所示空间直角坐标系,由(2)可知,
,
,
设为平面的法向量,,
取,
,
,,
,
.
同课章节目录
