13.3.2 等腰三角形的判定 课件(共16张PPT)
文档属性
| 名称 | 13.3.2 等腰三角形的判定 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 792.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-05 19:04:07 | ||
图片预览



文档简介
(共16张PPT)
等腰三角形的判定
复习旧知
两个三角形全等的判定方法有哪些?
两边一角
(SAS)
两角一边
(ASA,AAS)
三边 (SSS)
直角三角形(HL)
A
B
C
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
3、这个命题正确吗?你能证明吗?
怎么证明呢?
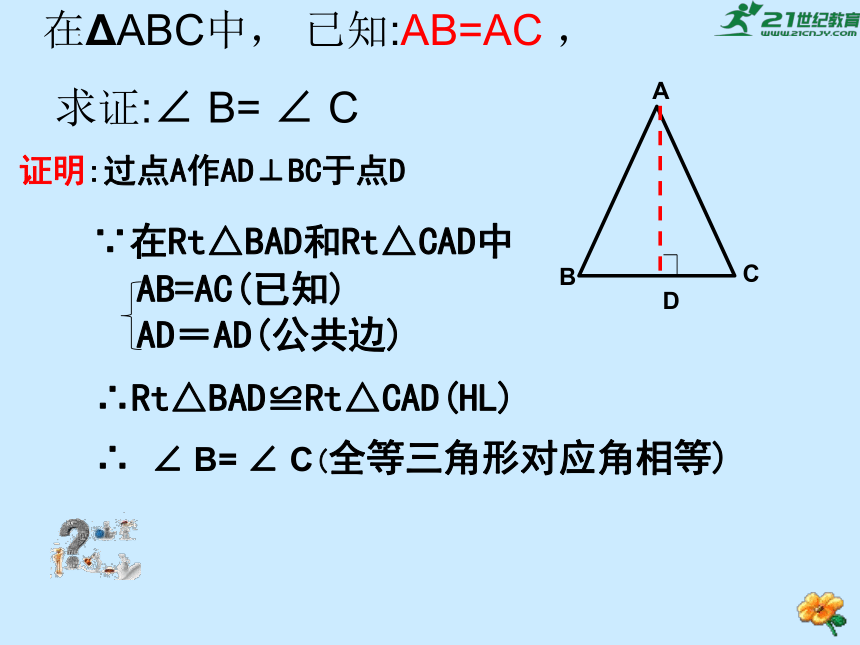
在ΔABC中, 已知:AB=AC ,
求证:∠ B= ∠ C
证明:过点A作AD⊥BC于点D
∵在Rt△BAD和Rt△CAD中
∴Rt△BAD≌Rt△CAD(HL)
∴ ∠ B= ∠ C(全等三角形对应角相等)
AB=AC(已知)
AD=AD(公共边)
B
C
A
D
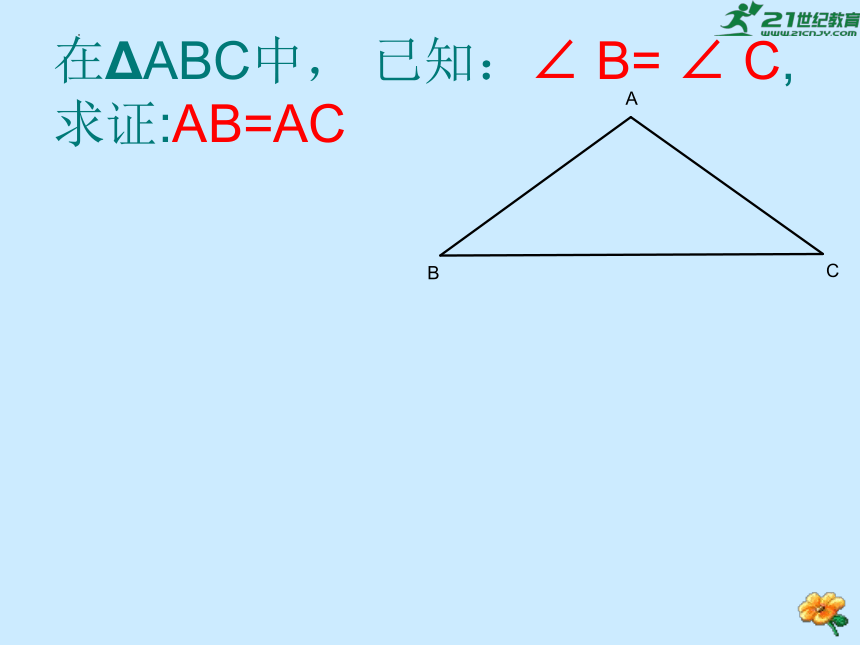
在ΔABC中, 已知:∠ B= ∠ C, 求证:AB=AC
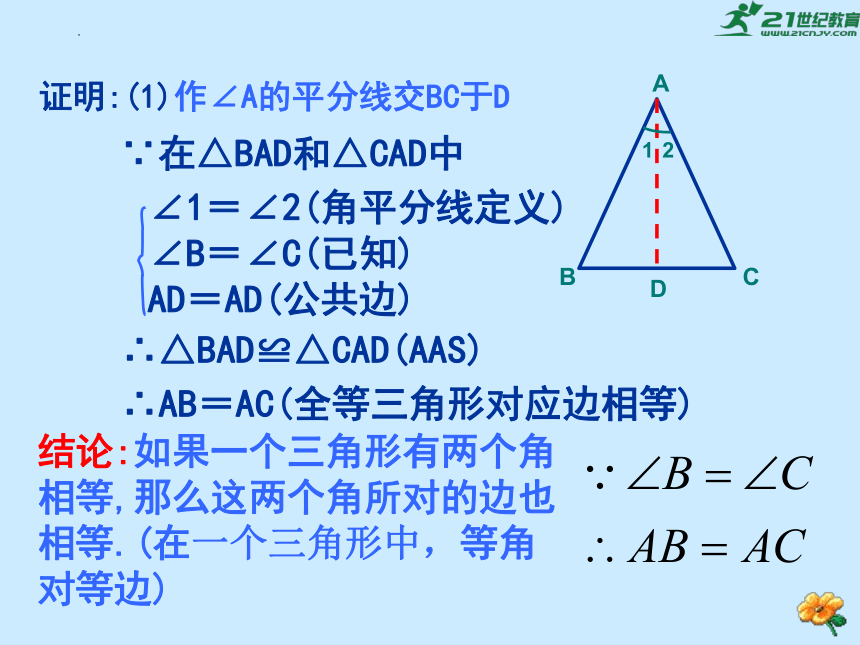
证明:(1)作∠A的平分线交BC于D
A
B
C
D
∴AB=AC(全等三角形对应边相等)
结论:如果一个三角形有两个角相等,那么这两个角所对的边也相等.(在一个三角形中,等角对等边)
1
2
∴△BAD≌△CAD(AAS)
∠1=∠2(角平分线定义) ∠B=∠C(已知)
AD=AD(公共边)
∵在△BAD和△CAD中
1、说出定理“等边三角形的三个内角都相等”
的逆命题,并证明该逆命题为真命题.
做一做
(等角对等边)
(等边对等角)
逆命题:
三个内角都相等的三角形是等边三角形.
已知: 如图,在△ABC中,
∠ A = ∠B=∠C.
求证: AB =BC =AC.
证明:
∵AD∥BC
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边)。
A
B
C
D
E
1
2
例2 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形吗?
如图:已知AD平分∠EAC,AD∥BC,求证:AB=AC
练习:如图在△ABC中AB=AC,过BA的延长线上点F作FD⊥BC于点D,交AC于点E.求证: △ AEF是等腰三角形
F
E
A
B
C
D
证明:∵在△ABC中,AB=AC
∴∠B=∠C(等边对等角)
∵FD ⊥BC(已知)
∴∠BDF=∠CDF= 90 °(垂直的定义)
∴∠B+∠F= 90 °, ∠C+∠CED= 90 °
∵ ∠B=∠C
∴∠F=∠CED(等角的余角相等)
又∵ ∠AEF=∠CED(对顶角相等)
∴∠F=∠AEF(等量代换)
∴AE=AF(等角对等边)
∴ △ AEF是等腰三角形
例:一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60 °角的AC方向前进至C,在C处测得∠C=30 ° .量出AC的长,它就是河宽(即A,B之间的距离).这个方法正确吗?请说明理由.
60 °
B
A
C
解:小聪的测量方法正确.理由如下:
∵ ∠DAC= ∠ABC+ ∠C
(三角形的外角的性质)
∴ ∠ABC= ∠DAC- ∠C
=60 ° -30 ° =30 °
∴ ∠ABC= ∠C
∴AB=AC(在一个三角形中,等角对等边)
D
应用
练习1
在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么
练习2
如图,已知∠A=36°,∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 图中的等腰三角形有
_______________________.
A
B
D
1
2
C
36°
72°
ABC, BCD, ABD
2. 如图,已知P、Q是△ABC的边BC上两点,
并且BP=PQ=QC=AP=AQ,求∠BAC的大小.
做一做
(等角对等边)
(等边对等角)
A
B
P
Q
C
实践与思考
画一个顶角为36°的等腰三角形,怎样将三角形分割成两个等腰三角形 说出你的方案.
画一个底角为36°的等腰三角形,怎样将三角形分割成两个等腰三角形 说出你的方案.
A
B
C
2.等角对等边
1.两边相等
等腰三角形的判定方法有哪些?
小结
谢
谢
大
家
!
等腰三角形的判定
复习旧知
两个三角形全等的判定方法有哪些?
两边一角
(SAS)
两角一边
(ASA,AAS)
三边 (SSS)
直角三角形(HL)
A
B
C
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
3、这个命题正确吗?你能证明吗?
怎么证明呢?
在ΔABC中, 已知:AB=AC ,
求证:∠ B= ∠ C
证明:过点A作AD⊥BC于点D
∵在Rt△BAD和Rt△CAD中
∴Rt△BAD≌Rt△CAD(HL)
∴ ∠ B= ∠ C(全等三角形对应角相等)
AB=AC(已知)
AD=AD(公共边)
B
C
A
D
在ΔABC中, 已知:∠ B= ∠ C, 求证:AB=AC
证明:(1)作∠A的平分线交BC于D
A
B
C
D
∴AB=AC(全等三角形对应边相等)
结论:如果一个三角形有两个角相等,那么这两个角所对的边也相等.(在一个三角形中,等角对等边)
1
2
∴△BAD≌△CAD(AAS)
∠1=∠2(角平分线定义) ∠B=∠C(已知)
AD=AD(公共边)
∵在△BAD和△CAD中
1、说出定理“等边三角形的三个内角都相等”
的逆命题,并证明该逆命题为真命题.
做一做
(等角对等边)
(等边对等角)
逆命题:
三个内角都相等的三角形是等边三角形.
已知: 如图,在△ABC中,
∠ A = ∠B=∠C.
求证: AB =BC =AC.
证明:
∵AD∥BC
∴∠1=∠B(两直线平行,
同位角相等),
∠2=∠C(两直线平行,
内错角相等)。
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等角对等边)。
A
B
C
D
E
1
2
例2 求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形吗?
如图:已知AD平分∠EAC,AD∥BC,求证:AB=AC
练习:如图在△ABC中AB=AC,过BA的延长线上点F作FD⊥BC于点D,交AC于点E.求证: △ AEF是等腰三角形
F
E
A
B
C
D
证明:∵在△ABC中,AB=AC
∴∠B=∠C(等边对等角)
∵FD ⊥BC(已知)
∴∠BDF=∠CDF= 90 °(垂直的定义)
∴∠B+∠F= 90 °, ∠C+∠CED= 90 °
∵ ∠B=∠C
∴∠F=∠CED(等角的余角相等)
又∵ ∠AEF=∠CED(对顶角相等)
∴∠F=∠AEF(等量代换)
∴AE=AF(等角对等边)
∴ △ AEF是等腰三角形
例:一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60 °角的AC方向前进至C,在C处测得∠C=30 ° .量出AC的长,它就是河宽(即A,B之间的距离).这个方法正确吗?请说明理由.
60 °
B
A
C
解:小聪的测量方法正确.理由如下:
∵ ∠DAC= ∠ABC+ ∠C
(三角形的外角的性质)
∴ ∠ABC= ∠DAC- ∠C
=60 ° -30 ° =30 °
∴ ∠ABC= ∠C
∴AB=AC(在一个三角形中,等角对等边)
D
应用
练习1
在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么
练习2
如图,已知∠A=36°,∠DBC=36°, ∠C=72°,则∠1= ,∠2= , 图中的等腰三角形有
_______________________.
A
B
D
1
2
C
36°
72°
ABC, BCD, ABD
2. 如图,已知P、Q是△ABC的边BC上两点,
并且BP=PQ=QC=AP=AQ,求∠BAC的大小.
做一做
(等角对等边)
(等边对等角)
A
B
P
Q
C
实践与思考
画一个顶角为36°的等腰三角形,怎样将三角形分割成两个等腰三角形 说出你的方案.
画一个底角为36°的等腰三角形,怎样将三角形分割成两个等腰三角形 说出你的方案.
A
B
C
2.等角对等边
1.两边相等
等腰三角形的判定方法有哪些?
小结
谢
谢
大
家
!
