苏科版九年级上册《14.3 欧姆定律》2023年同步练习卷(含解析)
文档属性
| 名称 | 苏科版九年级上册《14.3 欧姆定律》2023年同步练习卷(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 383.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-11-04 00:00:00 | ||
图片预览



文档简介
苏科版九年级上册《14.3 欧姆定律》2023年同步练习卷
一、选择题
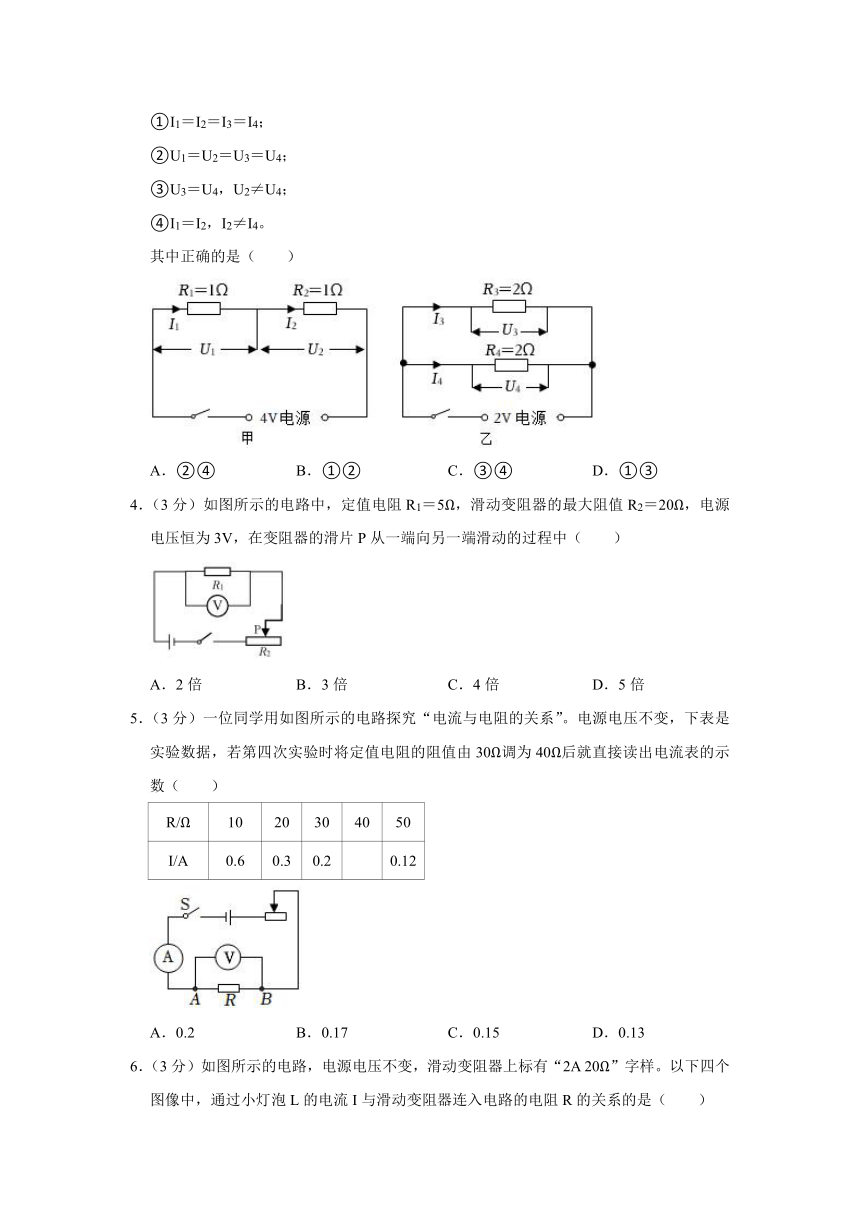
1.(3分)如图所示,是“探究电流与电压的关系”的实验电路图,R1为定值电阻,R2为滑动变阻器,电源电压恒定。闭合开关S,调节滑动变阻器滑片1、R2两端的电压的变化关系图象如图所示,其中正确的是( )
A. B.
C. D.
2.(3分)在如图所示的电路中,电源电压保持不变,R0为定值电阻闭合开关S后,将滑动变阻器的滑片P从中间某个位置移到最右端,电压表V1、V2和电流表的示数分别变化了ΔU1、ΔU2和ΔI。下列分析错误的是( )
A.不变 B.变大
C.不变 D.>
3.关于图甲、乙中各物理量的关系有以下的描述:
①I1=I2=I3=I4;
②U1=U2=U3=U4;
③U3=U4,U2≠U4;
④I1=I2,I2≠I4。
其中正确的是( )
A.②④ B.①② C.③④ D.①③
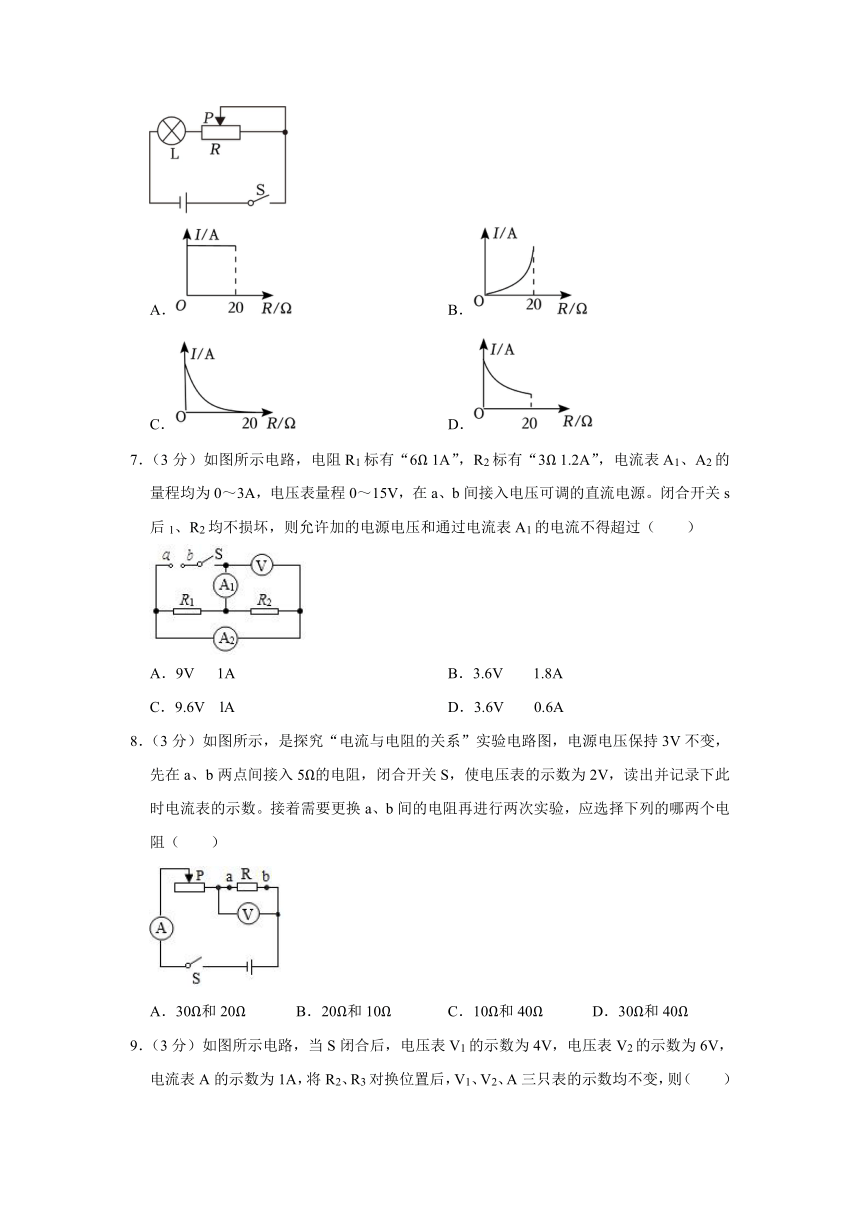
4.(3分)如图所示的电路中,定值电阻R1=5Ω,滑动变阻器的最大阻值R2=20Ω,电源电压恒为3V,在变阻器的滑片P从一端向另一端滑动的过程中( )
A.2倍 B.3倍 C.4倍 D.5倍
5.(3分)一位同学用如图所示的电路探究“电流与电阻的关系”。电源电压不变,下表是实验数据,若第四次实验时将定值电阻的阻值由30Ω调为40Ω后就直接读出电流表的示数( )
R/Ω 10 20 30 40 50
I/A 0.6 0.3 0.2 0.12
A.0.2 B.0.17 C.0.15 D.0.13
6.(3分)如图所示的电路,电源电压不变,滑动变阻器上标有“2A 20Ω”字样。以下四个图像中,通过小灯泡L的电流I与滑动变阻器连入电路的电阻R的关系的是( )
A. B.
C. D.
7.(3分)如图所示电路,电阻R1标有“6Ω 1A”,R2标有“3Ω 1.2A”,电流表A1、A2的量程均为0~3A,电压表量程0~15V,在a、b间接入电压可调的直流电源。闭合开关s后1、R2均不损坏,则允许加的电源电压和通过电流表A1的电流不得超过( )
A.9V 1A B.3.6V 1.8A
C.9.6V lA D.3.6V 0.6A
8.(3分)如图所示,是探究“电流与电阻的关系”实验电路图,电源电压保持3V不变,先在a、b两点间接入5Ω的电阻,闭合开关S,使电压表的示数为2V,读出并记录下此时电流表的示数。接着需要更换a、b间的电阻再进行两次实验,应选择下列的哪两个电阻( )
A.30Ω和20Ω B.20Ω和10Ω C.10Ω和40Ω D.30Ω和40Ω
9.(3分)如图所示电路,当S闭合后,电压表V1的示数为4V,电压表V2的示数为6V,电流表A的示数为1A,将R2、R3对换位置后,V1、V2、A三只表的示数均不变,则( )
A.通过三只电阻R1、R2、R3的电流之和是1A
B.R3的电阻值是2Ω
C.电源电压U=10V
D.R2两端的电压为3V
二、填空题
10.(3分)在某一温度下,两个电路元件甲和乙中的电流与电压的关系如图所示。若元件甲为R1,元件乙为R2,将元件甲、乙如图并联后接在电压为2V的电源两端,则A1与A2读数之比 ;若将元件甲、乙串联到3V的电源两端,则流过乙的电流是 A。
11.(3分)在相距80km的甲、乙两地间沿直线架设两条输电线,输电线的电阻与其长度成正比。若输电线在某处发生短路,为确定短路位置,并分别进行了如下测量:将测量仪连接ab时,电流表示数为0.4A,电流表示数为1.2A.由此判断短路位置离甲地距离为 km。
12.如图所示的电路,电阻R0为12Ω。闭合开关S1,将单刀双掷开关S2掷于b端,电阻R0与Rx是 联的,电压表示数为1.5V;将S2切换到a端,电压表示数为2.5V,则电阻Rx的阻值为 Ω。
13.(3分)如图所示电路,电源电压为6V,电阻R2为10Ω,滑动变阻器R1的最大阻值是20Ω,当滑片P移到a端时,电压表读数是 V,当滑片P移到b端时,电压表读数是 V。
14.(3分)如图所示电路,电源电压保持不变,当开关S1、S2都闭合时,电流表的示数为0.5A,电压表的示数为3V,只闭合开关S2,电流表的示数为0.2A。则定值电阻R1的阻值为 Ω,R2的阻值是 Ω。
15.(3分)如图甲所示的电路中,R1为定值电阻,R2为滑动变阻器,电源电压为6V,电流表示数I与电压表示数U的变化关系如图乙所示。闭合开关S后,电压表示数与电流表示数比值 (选填“变大”“变小”或“不变”),R1的阻值为 Ω,R2的最大值为 Ω。
16.(3分)如图甲所示,R2为电阻箱,调节R2时电流表示数I随之变化。如图乙所示是电阻箱阻值R2与电流表示数的倒数的图象。则定值电阻R1 Ω,电源电压 V。
三、实验探究题
17.用图甲所示电路探究电流与电阻的关系,电源电压为6V,四个定值电阻为5Ω、10Ω、20Ω和25Ω。
(1)请根据图甲所示电路图,用笔画线代替导线,将图乙实物图连接完整。
(2)连接电路时,开关应处于 状态,滑动变阻器的滑片应置于最 端。
(3)实验时,先将5Ω的定值电阻接入电路,并调节滑动变阻器的滑片,读出电流表的示数并记录。断开开关,将定值电阻换成I0Ω的再闭合开关 移动,直至电压表的示数为2V。
(4)依次更换不同的电阻完成实验,其中更换25Ω电阻时,电流表的读数应为 A。
(5)根据实验数据绘制的图象如图丙所示,可得出结论: 。
(6)为完成该实验,滑动变阻器的最大阻值应该不低于 Ω。
18.(3分)小明同学在“探究通过导体的电流与电阻的关系”时,他用如图所示的电路进行实验,可供选择的定值电阻分别为2.5Ω、5Ω、10Ω、15Ω、20Ω、25Ω。实验中电阻R两端的电压始终保持3V不变
(1)请用笔画线代替导线,将图中实物电路连接完整,要求滑动变阻器的滑片P向B端移动时接入电路的电阻变大。
(2)闭合开关,移动滑片P,记下多组对应的电压表和电流表的示数 (选填“减小实验误差”或“寻找普遍规律”)。
(3)实验中,不能被选用的电阻为 Ω。
(4)保证可用电阻均能正常进行实验,电源电压应该控制在 V至 V之间。
19.(3分)实验小组在探究电流与电阻的关系中,使用的器材有:电源、电流表、电压表、滑动变阻器各一个,开关一个(5Ω、10Ω、15Ω、20Ω、25Ω),导线若干,设计了如图甲所示的电路图。
(1)闭合开关前,电流表指针如图乙所示,对电流表的操作应该是 。
(2)小组在探究时,先将5Ω的电阻连入电路中,闭合开关后,电流表的示数如图丙所示,该示数为 A,接着断开开关,将5Ω电阻更换成10Ω电阻,接下来应做的操作是 ,直至电压表示数为 V,记下此时电流表的示数。
(3)实验小组收集的数据如下表,分析表中数据,发现第 次实验的数据存在错误,反思产生的原因,回忆是某次将定值电阻的阻值由 Ω变换为错误数据点对应阻值时(实验过程并未按表中序号顺序进行),未调节滑片P就读取电流而造成的。根据出现的数据,求出电源的电压是 V。
实验序号 1 2 3 4 5
电阻R/Ω 5 10 15 20 25
电流I/A 0.20 0.10 0.10 0.08
四、计算题
20.(3分)在如图所示的电路中,电源电压为6V不变,滑动变阻器上标有“20Ω 2A”字样。若电流表接0~0.6A、电压表接0~3V量程,移动滑动变阻器的滑片P,电流表示数的最大变化量为0.2A。
(1)移动滑动变阻器的滑片P,发现当电流最小时滑动变阻器无法达到20Ω,求此时电压表的示数U2。
(2)通过计算求出电阻R1可能的阻值。
苏科版九年级上册《14.3 欧姆定律》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【解答】解:
AB、由电路图可知1与滑动变阻器R2串联,电压表V7测定值电阻R1两端的电压,电压表V2测滑动变阻器R4两端的电压,电流表测电路中的电流,
由欧姆定律可得,R1两端的电压:U1=IR7,因R1的阻值不变,电流I与R1两端的电压成正比,A错误;
由串联电路的分压特点和欧姆定律可得,滑动变阻器两端的电压:U5=U﹣U1=U﹣IR1,因电源电压U和R3的阻值不变,所以2关系图象为一次函数图象,故CD错误。
故选:B。
2.【解答】解:由图可知,R0、R1与R6串联,电压表V1测R1两端的电压,电压表V7测R2两端的电压,电流表中的电流为流过R1和R5的电流;
滑动变阻器的滑片P从中间某个位置移到最右端时,滑动变阻器接入电路的电阻变大,根据欧姆定律可知;根据U=IR可知,R0、R1两端的电压变小,根据串联电路的电压规律可知,R5两端的电压变大;由于电源电压不变,R2两端的电压变化量等于R0和R5两端的电压变化量之和,所以R2两端的电压变化量大于R1两端的电压变化量,即ΔU6<ΔU2;
设滑动触头P向右滑动前后,电路中的电流分别为I1、I7,
由I=可得,R1两端的电压分别为:U1=I6R1,U1′=I3R1,
则ΔU1=U2′﹣U1=I2R5﹣I1R1=(I3﹣I1)R1=ΔIR4,即=R1,保持不变,故A正确;
由于ΔU2<ΔU2,所以<,故D正确;
根据并联电路的电压规律可知,R0、R1两端的电压变化量等于R6两端的电压的变化量,即:ΔU01=ΔU2;
滑片移动前后,R0、R3两端的电压为:U01=I1(R0+R3),U01′=I2(R0+R2);
则ΔU01=U01﹣U01′=I1(R0+R8)﹣I2(R0+R8)=(I2﹣I1)(R6+R1)=ΔI(R0+R4),
所以:=(R0+R1),由于ΔU01=ΔU2,则:=(R0+R2),保持不变,C正确。
故选:B。
3.【解答】解:图1中,R1与R4串联,
因串联电路中各处的电流相等,所以
I1=I2===2A,
两电阻两端的电压:
U7=U2=IR1=2A×1Ω=2V;
图2中,R3与R4并联,
因并联电路中各支路两端的电压相等,
所以,U4=U4=U′=2V,
通过两电阻的电流:
I5=I4===1A,
综上可知,I6=I2≠I3=I3,U1=U2=U3=U4,故②④正确。
故选:A。
4.【解答】解:当滑片滑到最右端时,滑动变阻器连入电阻为20Ω,则电路中电流:
I===0.12A;
电压表的示数U1=I×R5=0.12A×5Ω=7.6V;
当滑片滑到最左端时,滑动变阻器连入电阻为0,R2两端电压等于电源电压,即U1′=3V;
电压表的示数的最大值U6′与最小值U1的比值:U1′:U8=3V:0.2V=5:1。
故选:D。
5.【解答】解:研究通过导体的电流与电阻的关系要保持导体两端的电压不变,
电阻两端的电压U电阻箱=I1R1=2.6A×10Ω=6V,
当电阻R的阻值为40Ω时,电路中的电流应该为:I′==,
小华将电阻R的阻值从30Ω调为40Ω后,要保持电阻两端电压不变,
应向右移动滑动变阻器滑片,使滑动变阻器接入电路的阻值变大,
从而使电阻两端电压减小保持不变,因此,电路中的电流应该大于0.15A而小于8.2A,
故选:B。
6.【解答】解:此电路为串联电路,通过小灯泡的电流和通过滑动变阻器的电流相等,电压一定时,所以可排除A,当滑动变阻器的阻值最大为20Ω时,但不可能为0所以可排除C选项。
故选:D。
7.【解答】解:开关闭合后,两电阻并联,电流表A1测干路电流,电流表A2测通过电阻R5的电流,等效电路图如下图所示:
(1)∵电阻R1标有“6Ω 8A”,R2标有“3Ω 2.2A”,
∴根据欧姆定律可得:
电阻R1两端允许的最大电压为U2=I1R1=5A×6Ω=6V,
电阻R6两端允许的最大电压为U2=I2R6=1.2A×3Ω=3.6V,
∵并联电路,各支路电压相等,
∴为了保护电阻R8,电源电压不能超过3.6V。
(2)此时通过电阻R6的电流为:
I1===8.6A,
∵并联电路中干路电流等于各支路电流之和,
∴干路电流表A1的示数I=I2+I2=0.7A+1.2A=4.8A。
故选:B。
8.【解答】解:探究“电流与电阻的关系”实验中应控制电阻两端的电压即电压表的示数不变,
因串联电路中总电压等于各分电压之和,
所以,滑动变阻器两端的电压:
U滑=U﹣UR=3V﹣2V=6V,
因串联电路中各处的电流相等,
所以,根据欧姆定律可得:
====,
当滑动变阻器接入电路中的电阻为10Ω时,定值电阻的最大阻值:
Rmax=2R滑max=6×10Ω=20Ω,
即定值电阻的最大阻值不能超过20Ω,
结合选项可知,B符合题意。
故选:B。
9.【解答】解:A、因为三个电阻串联,故电路中电流的都相等1、R2、R8的电流均为1A;故A选项错误;
B、V1测R4、R2的电压,V2测R2、R3的电压,由欧姆定律I=
R1+R3===4Ω,
R2+R3===6Ω,
将R2和R2对换位置后,电流表,说明:R2=R3,则R5=R3=3Ω,R8=1Ω;B错误;
C、由电阻的串联和欧姆定律
U=IR=I(R1+R2+R3)=1A×(7Ω+3Ω+3Ω)=3V;C错误;
D、由欧姆定律,R2两端的电压:U2=IR6=1A×3Ω=2V.D正确。
故选:D。
二、填空题
10.【解答】解:由电路图知R1和R2并联,电流表A6测量电阻R2的电流,电流表A2测量干路的总电流;
(1)因并联电路中各支路两端的电压相等,
所以,将元件甲,U甲=U乙=2V,
由图象可知,I甲=0.4A,I乙=7.2A,
所以电流表A1的示数为5.2A,电流表A2的示数为2.2A+0.5A=0.6A,
则A3与A2读数之比为:0.4A:0.6A=7:3;
(2)将元件甲、乙串联后接在电压为3V的电源两端时,
因串联电路中各处的电流相等,且总电压等于各分电压之和,
所以,由图象可知甲′=I乙′=3.2A时,U甲=1V、U乙=5V,符合电源电压为3V,
则流过元件乙的电流是0.8A。
故答案为:1:3;3.2。
11.【解答】解:已知输电线的电阻与其长度成正比,设每km输电线的电阻为R0,
导线的短路位置离甲地为s,短路位置离乙地为80km﹣s,
则Rab=2sR3,Rcd=2(80km﹣s)R0,
由欧姆定律得:U=IabRab,U=IcdRcd,
所以,IabRab=IcdRcd,
即:4.4A×2sR2=1.2A×8(80km﹣s)R0,
解得:s=60km;
故答案为:60。
12.【解答】解:已知电阻R0与Rx串联,闭合开关S1,将单刀双掷开关S3掷于a端时,电压表测量总电压2切换到b端时,电压表测量电阻R0两端的电压,
由串联电路电流处处相等和串联电路中各用电器两端电压之和等于电源电压可得:
=,
即:=,
解得:Rx=4Ω。
故答案为:串;8。
13.【解答】解:当滑片P移到a端时,电压表测电源的电压;
当滑片P移到b端时,电压表测R2两端的电压,
电路中的电流I===0.3A,
电压表的示数为U2=IR2=5.2A×10Ω=2V。
故答案为:7;2。
14.【解答】解:(1)当开关S1、S2都闭合时,两电阻并联,则电源的电压U=3V1支路的电流,
由I=可知1的阻值:
R3===6Ω;
(2)将电压表、电流表的位置互换8,两电阻串联,电压表测电源的电压,
由I=可知,
此时电路中的总电阻:
R===15Ω,
因串联电路中总电阻等于各分电阻之和,
所以,电阻R2的阻值:
R2=R﹣R8=15Ω﹣6Ω=9Ω。
故答案为:2;9。
15.【解答】解:由图甲可知,两电阻串联2两端的电压,电流表测电路中的电流。
电压表示数与电流表示数比值即为滑动变阻器的电阻,当滑片P从b端移动到a端时,所以滑片P从b端移动到a端;
当滑动变阻器接入电路中的电阻为0时,电路中的电流最大7=1.2A,
根据欧姆定律可得,
R4===5Ω;
当滑动变阻器接入电路中的电阻最大时,电路中的电流最小,I8=0.4A,U8=4V,
根据I=得,滑动变阻器的最大阻值:
R2===10Ω。
故答案为:变小;5;10。
16.【解答】解:由电路图可知,R1与R2串联,电流表测电路中的电流,
由图乙可知,当R8=0Ω时,=2A﹣1,则电路中的电流I1=3.5A,
此时只有R1接入电路,则由I=,电源的电压:
U=I8R1=0.2A×R1,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
当R2=10Ω时,=6A﹣1,则电路中的电流I7=A,
因串联电路中总电阻等于各分电阻之和,
所以,电源的电压:
U=I7(R1+R2)=A×(R1+10Ω),﹣﹣﹣﹣﹣﹣﹣﹣②
因电源的电压不变,
所以,8.5A×R1=A×(R1+10Ω),
解得:R4=5Ω,
电源的电压U=I1R5=0.5A×2Ω=2.5V。
故答案为:5;2.5。
三、实验探究题
17.【解答】解:(1)由图丙可知,定值电阻两端电压为UV=IR=0.4A×8Ω=……=0.1A×20Ω=4V,故电压表选用小量程并联在定值电阻两端
;
(2)为了保护电路,连接电路时,滑动变阻器的滑片应置于阻值最大处;
(3)实验中,当把5Ω的电阻换成10Ω的电阻后,电阻两端的电压变大,根据串联电路电压的规律,由分压原理,故应把滑动变阻器滑片向右移动,直至电压表的示数为2V;
(4)研究电流与电阻的关系时,定值电阻两端的电压不变,更换25Ω电阻时
I7===4.08A;
(5)由(1)可知,定值电阻的电流与电阻的乘积为一定值,通过导体的电流与导体的电阻成反比;
(6)实验中使用的定值电阻阻值最大为25Ω,定值电阻两端的电压始终保持UV=2V,根据串联电路电压的规律滑=U﹣UV=6V﹣3V=4V,滑动变阻器分得的电压为电压表示数的,根据分压原理,滑动变阻器连入电路中的电阻为:R滑=2×25Ω=50Ω,即所选择的滑动变阻器的最大阻值不能小于50Ω。
故答案为:(1)见解答图;(2)断开;右;(4)0.08,通过导体的电流与导体的电阻成反比。
18.【解答】解:(1)滑动变阻器的滑片P向B端移动时接入电路的电阻变大,说明滑动变阻器接入电路的电阻丝变长,如图所示:
;
(2)闭合开关,移动滑片P,多次测量的目的是避免实验的偶然性;
(3)因为电流表的量程为0~0.5A,滑动变阻器允许通过的最大电流为1A,电路中的最大电流为0.5A,
由欧姆定律可知,定值电阻的最小阻值:R最小===5Ω>2.3Ω;
(4)探究电流与电阻的关系,应保持电阻两端的电压不变,定值电阻两端的电压为UR=3V,由串联电路的特点可知,此时电源电压为最小:U最小=UV=3V,
当电阻最大为25Ω且变阻器接入最大阻值时,电源电压为最大=,所以电源电压最大值:UE=×UR=×5V=4.8V。
故答案为:(1)如图所示;(2)寻找普遍规律;(4)8。
19.【解答】解:(1)闭合开关前,电流表指针如图乙所示。
(2)电压表的示数为:U=IR=5Ω×0.3A=10Ω×0.20A=﹣﹣﹣﹣﹣=2V;
电流表的示数如图丙所示,电流表选用小量程,该示数为6.40A;
接着断开开关,将5Ω电阻更换成10Ω电阻,其分得的电压增大,即应保持电阻两端的电压不变,由分压原理,所以滑片应向左移动变阻器的滑片,记下此时电流表的示数;
(3)研究电流与电阻关系时,要控制电阻的电压大小不变,
由表中数据知:
UV=IR=0.8A×5Ω=0.3A×10Ω=0.1A×20Ω=4.08A×25Ω≠0.10A×15Ω,故分析表中数据;
因电源电压U一定,电压表示数(2V)一定,变阻器的电压也是一定的,
故变阻器的电压与定值电阻的电压之比为一定值,由分压原理,变阻器连入电路的电阻越大;
第2次实验,正确操作时
I3==≈0.13A>0.10A,
故变阻器连入的电阻应比正常情况下大,
故只有可能是第3、5次(定值电阻分别为20Ω和25Ω)实验时未调节滑片P就读取电流而造成的,
若是第4次未调节滑片P就读取电流而造成的,根据欧姆定律和串联电路电压的规律
R滑I4+U4=R滑I3+U6,
代入数据,但R滑×0.1A+2.5V≠0.7A×R滑+2V,与电源电压相等矛盾;
若是第5次未调节滑片P就读取电流而造成的,同理有:
U=R滑×8.1A+1.4V=0.08A×R滑+2V,
解之:R滑=25Ω,
电源电压:U=2V;
故反思产生的原因,回忆是某次将定值电阻的阻值由25Ω变换为错误数据点对应阻值时(实验过程并未按表中序号顺序进行),根据现有的数据。
故答案为:(1)将电流表指针调零;(2)0.40;2;(3)6;4。
四、计算题
20.【解答】解:由电路图可知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。
(1)移动变阻器的滑片P,当电流最小时滑动变阻器无法达到20Ω,
则此时电压表示数已达到量程,即电压表的示数U2=3V;
(2)当电压表的示数为4V时电路中的电流最小,
因串联电路中总电压等于各分电压之和,
所以,电路中的最小电流:
I小====;
若电路中的最大电流I大=0.6A,
因移动变阻器的滑片P,电流表示数的最大变化量为8.2A,
所以,I大﹣I小=0.7A﹣=7.2A,
解得:R1=3.5Ω;
若电路中的最大电流为:I大==<0.6A,
则:I大﹣I小=﹣==0.2A,
解得:R4=15Ω;
综上,电阻R1可能的阻值为7.5Ω、15Ω。
答:(1)移动滑动变阻器的滑片P,发现当电流最小时滑动变阻器无法达到20Ω2为3V。
(2)电阻R2可能的阻值为7.5Ω、15Ω。
一、选择题
1.(3分)如图所示,是“探究电流与电压的关系”的实验电路图,R1为定值电阻,R2为滑动变阻器,电源电压恒定。闭合开关S,调节滑动变阻器滑片1、R2两端的电压的变化关系图象如图所示,其中正确的是( )
A. B.
C. D.
2.(3分)在如图所示的电路中,电源电压保持不变,R0为定值电阻闭合开关S后,将滑动变阻器的滑片P从中间某个位置移到最右端,电压表V1、V2和电流表的示数分别变化了ΔU1、ΔU2和ΔI。下列分析错误的是( )
A.不变 B.变大
C.不变 D.>
3.关于图甲、乙中各物理量的关系有以下的描述:
①I1=I2=I3=I4;
②U1=U2=U3=U4;
③U3=U4,U2≠U4;
④I1=I2,I2≠I4。
其中正确的是( )
A.②④ B.①② C.③④ D.①③
4.(3分)如图所示的电路中,定值电阻R1=5Ω,滑动变阻器的最大阻值R2=20Ω,电源电压恒为3V,在变阻器的滑片P从一端向另一端滑动的过程中( )
A.2倍 B.3倍 C.4倍 D.5倍
5.(3分)一位同学用如图所示的电路探究“电流与电阻的关系”。电源电压不变,下表是实验数据,若第四次实验时将定值电阻的阻值由30Ω调为40Ω后就直接读出电流表的示数( )
R/Ω 10 20 30 40 50
I/A 0.6 0.3 0.2 0.12
A.0.2 B.0.17 C.0.15 D.0.13
6.(3分)如图所示的电路,电源电压不变,滑动变阻器上标有“2A 20Ω”字样。以下四个图像中,通过小灯泡L的电流I与滑动变阻器连入电路的电阻R的关系的是( )
A. B.
C. D.
7.(3分)如图所示电路,电阻R1标有“6Ω 1A”,R2标有“3Ω 1.2A”,电流表A1、A2的量程均为0~3A,电压表量程0~15V,在a、b间接入电压可调的直流电源。闭合开关s后1、R2均不损坏,则允许加的电源电压和通过电流表A1的电流不得超过( )
A.9V 1A B.3.6V 1.8A
C.9.6V lA D.3.6V 0.6A
8.(3分)如图所示,是探究“电流与电阻的关系”实验电路图,电源电压保持3V不变,先在a、b两点间接入5Ω的电阻,闭合开关S,使电压表的示数为2V,读出并记录下此时电流表的示数。接着需要更换a、b间的电阻再进行两次实验,应选择下列的哪两个电阻( )
A.30Ω和20Ω B.20Ω和10Ω C.10Ω和40Ω D.30Ω和40Ω
9.(3分)如图所示电路,当S闭合后,电压表V1的示数为4V,电压表V2的示数为6V,电流表A的示数为1A,将R2、R3对换位置后,V1、V2、A三只表的示数均不变,则( )
A.通过三只电阻R1、R2、R3的电流之和是1A
B.R3的电阻值是2Ω
C.电源电压U=10V
D.R2两端的电压为3V
二、填空题
10.(3分)在某一温度下,两个电路元件甲和乙中的电流与电压的关系如图所示。若元件甲为R1,元件乙为R2,将元件甲、乙如图并联后接在电压为2V的电源两端,则A1与A2读数之比 ;若将元件甲、乙串联到3V的电源两端,则流过乙的电流是 A。
11.(3分)在相距80km的甲、乙两地间沿直线架设两条输电线,输电线的电阻与其长度成正比。若输电线在某处发生短路,为确定短路位置,并分别进行了如下测量:将测量仪连接ab时,电流表示数为0.4A,电流表示数为1.2A.由此判断短路位置离甲地距离为 km。
12.如图所示的电路,电阻R0为12Ω。闭合开关S1,将单刀双掷开关S2掷于b端,电阻R0与Rx是 联的,电压表示数为1.5V;将S2切换到a端,电压表示数为2.5V,则电阻Rx的阻值为 Ω。
13.(3分)如图所示电路,电源电压为6V,电阻R2为10Ω,滑动变阻器R1的最大阻值是20Ω,当滑片P移到a端时,电压表读数是 V,当滑片P移到b端时,电压表读数是 V。
14.(3分)如图所示电路,电源电压保持不变,当开关S1、S2都闭合时,电流表的示数为0.5A,电压表的示数为3V,只闭合开关S2,电流表的示数为0.2A。则定值电阻R1的阻值为 Ω,R2的阻值是 Ω。
15.(3分)如图甲所示的电路中,R1为定值电阻,R2为滑动变阻器,电源电压为6V,电流表示数I与电压表示数U的变化关系如图乙所示。闭合开关S后,电压表示数与电流表示数比值 (选填“变大”“变小”或“不变”),R1的阻值为 Ω,R2的最大值为 Ω。
16.(3分)如图甲所示,R2为电阻箱,调节R2时电流表示数I随之变化。如图乙所示是电阻箱阻值R2与电流表示数的倒数的图象。则定值电阻R1 Ω,电源电压 V。
三、实验探究题
17.用图甲所示电路探究电流与电阻的关系,电源电压为6V,四个定值电阻为5Ω、10Ω、20Ω和25Ω。
(1)请根据图甲所示电路图,用笔画线代替导线,将图乙实物图连接完整。
(2)连接电路时,开关应处于 状态,滑动变阻器的滑片应置于最 端。
(3)实验时,先将5Ω的定值电阻接入电路,并调节滑动变阻器的滑片,读出电流表的示数并记录。断开开关,将定值电阻换成I0Ω的再闭合开关 移动,直至电压表的示数为2V。
(4)依次更换不同的电阻完成实验,其中更换25Ω电阻时,电流表的读数应为 A。
(5)根据实验数据绘制的图象如图丙所示,可得出结论: 。
(6)为完成该实验,滑动变阻器的最大阻值应该不低于 Ω。
18.(3分)小明同学在“探究通过导体的电流与电阻的关系”时,他用如图所示的电路进行实验,可供选择的定值电阻分别为2.5Ω、5Ω、10Ω、15Ω、20Ω、25Ω。实验中电阻R两端的电压始终保持3V不变
(1)请用笔画线代替导线,将图中实物电路连接完整,要求滑动变阻器的滑片P向B端移动时接入电路的电阻变大。
(2)闭合开关,移动滑片P,记下多组对应的电压表和电流表的示数 (选填“减小实验误差”或“寻找普遍规律”)。
(3)实验中,不能被选用的电阻为 Ω。
(4)保证可用电阻均能正常进行实验,电源电压应该控制在 V至 V之间。
19.(3分)实验小组在探究电流与电阻的关系中,使用的器材有:电源、电流表、电压表、滑动变阻器各一个,开关一个(5Ω、10Ω、15Ω、20Ω、25Ω),导线若干,设计了如图甲所示的电路图。
(1)闭合开关前,电流表指针如图乙所示,对电流表的操作应该是 。
(2)小组在探究时,先将5Ω的电阻连入电路中,闭合开关后,电流表的示数如图丙所示,该示数为 A,接着断开开关,将5Ω电阻更换成10Ω电阻,接下来应做的操作是 ,直至电压表示数为 V,记下此时电流表的示数。
(3)实验小组收集的数据如下表,分析表中数据,发现第 次实验的数据存在错误,反思产生的原因,回忆是某次将定值电阻的阻值由 Ω变换为错误数据点对应阻值时(实验过程并未按表中序号顺序进行),未调节滑片P就读取电流而造成的。根据出现的数据,求出电源的电压是 V。
实验序号 1 2 3 4 5
电阻R/Ω 5 10 15 20 25
电流I/A 0.20 0.10 0.10 0.08
四、计算题
20.(3分)在如图所示的电路中,电源电压为6V不变,滑动变阻器上标有“20Ω 2A”字样。若电流表接0~0.6A、电压表接0~3V量程,移动滑动变阻器的滑片P,电流表示数的最大变化量为0.2A。
(1)移动滑动变阻器的滑片P,发现当电流最小时滑动变阻器无法达到20Ω,求此时电压表的示数U2。
(2)通过计算求出电阻R1可能的阻值。
苏科版九年级上册《14.3 欧姆定律》2023年同步练习卷
参考答案与试题解析
一、选择题
1.【解答】解:
AB、由电路图可知1与滑动变阻器R2串联,电压表V7测定值电阻R1两端的电压,电压表V2测滑动变阻器R4两端的电压,电流表测电路中的电流,
由欧姆定律可得,R1两端的电压:U1=IR7,因R1的阻值不变,电流I与R1两端的电压成正比,A错误;
由串联电路的分压特点和欧姆定律可得,滑动变阻器两端的电压:U5=U﹣U1=U﹣IR1,因电源电压U和R3的阻值不变,所以2关系图象为一次函数图象,故CD错误。
故选:B。
2.【解答】解:由图可知,R0、R1与R6串联,电压表V1测R1两端的电压,电压表V7测R2两端的电压,电流表中的电流为流过R1和R5的电流;
滑动变阻器的滑片P从中间某个位置移到最右端时,滑动变阻器接入电路的电阻变大,根据欧姆定律可知;根据U=IR可知,R0、R1两端的电压变小,根据串联电路的电压规律可知,R5两端的电压变大;由于电源电压不变,R2两端的电压变化量等于R0和R5两端的电压变化量之和,所以R2两端的电压变化量大于R1两端的电压变化量,即ΔU6<ΔU2;
设滑动触头P向右滑动前后,电路中的电流分别为I1、I7,
由I=可得,R1两端的电压分别为:U1=I6R1,U1′=I3R1,
则ΔU1=U2′﹣U1=I2R5﹣I1R1=(I3﹣I1)R1=ΔIR4,即=R1,保持不变,故A正确;
由于ΔU2<ΔU2,所以<,故D正确;
根据并联电路的电压规律可知,R0、R1两端的电压变化量等于R6两端的电压的变化量,即:ΔU01=ΔU2;
滑片移动前后,R0、R3两端的电压为:U01=I1(R0+R3),U01′=I2(R0+R2);
则ΔU01=U01﹣U01′=I1(R0+R8)﹣I2(R0+R8)=(I2﹣I1)(R6+R1)=ΔI(R0+R4),
所以:=(R0+R1),由于ΔU01=ΔU2,则:=(R0+R2),保持不变,C正确。
故选:B。
3.【解答】解:图1中,R1与R4串联,
因串联电路中各处的电流相等,所以
I1=I2===2A,
两电阻两端的电压:
U7=U2=IR1=2A×1Ω=2V;
图2中,R3与R4并联,
因并联电路中各支路两端的电压相等,
所以,U4=U4=U′=2V,
通过两电阻的电流:
I5=I4===1A,
综上可知,I6=I2≠I3=I3,U1=U2=U3=U4,故②④正确。
故选:A。
4.【解答】解:当滑片滑到最右端时,滑动变阻器连入电阻为20Ω,则电路中电流:
I===0.12A;
电压表的示数U1=I×R5=0.12A×5Ω=7.6V;
当滑片滑到最左端时,滑动变阻器连入电阻为0,R2两端电压等于电源电压,即U1′=3V;
电压表的示数的最大值U6′与最小值U1的比值:U1′:U8=3V:0.2V=5:1。
故选:D。
5.【解答】解:研究通过导体的电流与电阻的关系要保持导体两端的电压不变,
电阻两端的电压U电阻箱=I1R1=2.6A×10Ω=6V,
当电阻R的阻值为40Ω时,电路中的电流应该为:I′==,
小华将电阻R的阻值从30Ω调为40Ω后,要保持电阻两端电压不变,
应向右移动滑动变阻器滑片,使滑动变阻器接入电路的阻值变大,
从而使电阻两端电压减小保持不变,因此,电路中的电流应该大于0.15A而小于8.2A,
故选:B。
6.【解答】解:此电路为串联电路,通过小灯泡的电流和通过滑动变阻器的电流相等,电压一定时,所以可排除A,当滑动变阻器的阻值最大为20Ω时,但不可能为0所以可排除C选项。
故选:D。
7.【解答】解:开关闭合后,两电阻并联,电流表A1测干路电流,电流表A2测通过电阻R5的电流,等效电路图如下图所示:
(1)∵电阻R1标有“6Ω 8A”,R2标有“3Ω 2.2A”,
∴根据欧姆定律可得:
电阻R1两端允许的最大电压为U2=I1R1=5A×6Ω=6V,
电阻R6两端允许的最大电压为U2=I2R6=1.2A×3Ω=3.6V,
∵并联电路,各支路电压相等,
∴为了保护电阻R8,电源电压不能超过3.6V。
(2)此时通过电阻R6的电流为:
I1===8.6A,
∵并联电路中干路电流等于各支路电流之和,
∴干路电流表A1的示数I=I2+I2=0.7A+1.2A=4.8A。
故选:B。
8.【解答】解:探究“电流与电阻的关系”实验中应控制电阻两端的电压即电压表的示数不变,
因串联电路中总电压等于各分电压之和,
所以,滑动变阻器两端的电压:
U滑=U﹣UR=3V﹣2V=6V,
因串联电路中各处的电流相等,
所以,根据欧姆定律可得:
====,
当滑动变阻器接入电路中的电阻为10Ω时,定值电阻的最大阻值:
Rmax=2R滑max=6×10Ω=20Ω,
即定值电阻的最大阻值不能超过20Ω,
结合选项可知,B符合题意。
故选:B。
9.【解答】解:A、因为三个电阻串联,故电路中电流的都相等1、R2、R8的电流均为1A;故A选项错误;
B、V1测R4、R2的电压,V2测R2、R3的电压,由欧姆定律I=
R1+R3===4Ω,
R2+R3===6Ω,
将R2和R2对换位置后,电流表,说明:R2=R3,则R5=R3=3Ω,R8=1Ω;B错误;
C、由电阻的串联和欧姆定律
U=IR=I(R1+R2+R3)=1A×(7Ω+3Ω+3Ω)=3V;C错误;
D、由欧姆定律,R2两端的电压:U2=IR6=1A×3Ω=2V.D正确。
故选:D。
二、填空题
10.【解答】解:由电路图知R1和R2并联,电流表A6测量电阻R2的电流,电流表A2测量干路的总电流;
(1)因并联电路中各支路两端的电压相等,
所以,将元件甲,U甲=U乙=2V,
由图象可知,I甲=0.4A,I乙=7.2A,
所以电流表A1的示数为5.2A,电流表A2的示数为2.2A+0.5A=0.6A,
则A3与A2读数之比为:0.4A:0.6A=7:3;
(2)将元件甲、乙串联后接在电压为3V的电源两端时,
因串联电路中各处的电流相等,且总电压等于各分电压之和,
所以,由图象可知甲′=I乙′=3.2A时,U甲=1V、U乙=5V,符合电源电压为3V,
则流过元件乙的电流是0.8A。
故答案为:1:3;3.2。
11.【解答】解:已知输电线的电阻与其长度成正比,设每km输电线的电阻为R0,
导线的短路位置离甲地为s,短路位置离乙地为80km﹣s,
则Rab=2sR3,Rcd=2(80km﹣s)R0,
由欧姆定律得:U=IabRab,U=IcdRcd,
所以,IabRab=IcdRcd,
即:4.4A×2sR2=1.2A×8(80km﹣s)R0,
解得:s=60km;
故答案为:60。
12.【解答】解:已知电阻R0与Rx串联,闭合开关S1,将单刀双掷开关S3掷于a端时,电压表测量总电压2切换到b端时,电压表测量电阻R0两端的电压,
由串联电路电流处处相等和串联电路中各用电器两端电压之和等于电源电压可得:
=,
即:=,
解得:Rx=4Ω。
故答案为:串;8。
13.【解答】解:当滑片P移到a端时,电压表测电源的电压;
当滑片P移到b端时,电压表测R2两端的电压,
电路中的电流I===0.3A,
电压表的示数为U2=IR2=5.2A×10Ω=2V。
故答案为:7;2。
14.【解答】解:(1)当开关S1、S2都闭合时,两电阻并联,则电源的电压U=3V1支路的电流,
由I=可知1的阻值:
R3===6Ω;
(2)将电压表、电流表的位置互换8,两电阻串联,电压表测电源的电压,
由I=可知,
此时电路中的总电阻:
R===15Ω,
因串联电路中总电阻等于各分电阻之和,
所以,电阻R2的阻值:
R2=R﹣R8=15Ω﹣6Ω=9Ω。
故答案为:2;9。
15.【解答】解:由图甲可知,两电阻串联2两端的电压,电流表测电路中的电流。
电压表示数与电流表示数比值即为滑动变阻器的电阻,当滑片P从b端移动到a端时,所以滑片P从b端移动到a端;
当滑动变阻器接入电路中的电阻为0时,电路中的电流最大7=1.2A,
根据欧姆定律可得,
R4===5Ω;
当滑动变阻器接入电路中的电阻最大时,电路中的电流最小,I8=0.4A,U8=4V,
根据I=得,滑动变阻器的最大阻值:
R2===10Ω。
故答案为:变小;5;10。
16.【解答】解:由电路图可知,R1与R2串联,电流表测电路中的电流,
由图乙可知,当R8=0Ω时,=2A﹣1,则电路中的电流I1=3.5A,
此时只有R1接入电路,则由I=,电源的电压:
U=I8R1=0.2A×R1,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
当R2=10Ω时,=6A﹣1,则电路中的电流I7=A,
因串联电路中总电阻等于各分电阻之和,
所以,电源的电压:
U=I7(R1+R2)=A×(R1+10Ω),﹣﹣﹣﹣﹣﹣﹣﹣②
因电源的电压不变,
所以,8.5A×R1=A×(R1+10Ω),
解得:R4=5Ω,
电源的电压U=I1R5=0.5A×2Ω=2.5V。
故答案为:5;2.5。
三、实验探究题
17.【解答】解:(1)由图丙可知,定值电阻两端电压为UV=IR=0.4A×8Ω=……=0.1A×20Ω=4V,故电压表选用小量程并联在定值电阻两端
;
(2)为了保护电路,连接电路时,滑动变阻器的滑片应置于阻值最大处;
(3)实验中,当把5Ω的电阻换成10Ω的电阻后,电阻两端的电压变大,根据串联电路电压的规律,由分压原理,故应把滑动变阻器滑片向右移动,直至电压表的示数为2V;
(4)研究电流与电阻的关系时,定值电阻两端的电压不变,更换25Ω电阻时
I7===4.08A;
(5)由(1)可知,定值电阻的电流与电阻的乘积为一定值,通过导体的电流与导体的电阻成反比;
(6)实验中使用的定值电阻阻值最大为25Ω,定值电阻两端的电压始终保持UV=2V,根据串联电路电压的规律滑=U﹣UV=6V﹣3V=4V,滑动变阻器分得的电压为电压表示数的,根据分压原理,滑动变阻器连入电路中的电阻为:R滑=2×25Ω=50Ω,即所选择的滑动变阻器的最大阻值不能小于50Ω。
故答案为:(1)见解答图;(2)断开;右;(4)0.08,通过导体的电流与导体的电阻成反比。
18.【解答】解:(1)滑动变阻器的滑片P向B端移动时接入电路的电阻变大,说明滑动变阻器接入电路的电阻丝变长,如图所示:
;
(2)闭合开关,移动滑片P,多次测量的目的是避免实验的偶然性;
(3)因为电流表的量程为0~0.5A,滑动变阻器允许通过的最大电流为1A,电路中的最大电流为0.5A,
由欧姆定律可知,定值电阻的最小阻值:R最小===5Ω>2.3Ω;
(4)探究电流与电阻的关系,应保持电阻两端的电压不变,定值电阻两端的电压为UR=3V,由串联电路的特点可知,此时电源电压为最小:U最小=UV=3V,
当电阻最大为25Ω且变阻器接入最大阻值时,电源电压为最大=,所以电源电压最大值:UE=×UR=×5V=4.8V。
故答案为:(1)如图所示;(2)寻找普遍规律;(4)8。
19.【解答】解:(1)闭合开关前,电流表指针如图乙所示。
(2)电压表的示数为:U=IR=5Ω×0.3A=10Ω×0.20A=﹣﹣﹣﹣﹣=2V;
电流表的示数如图丙所示,电流表选用小量程,该示数为6.40A;
接着断开开关,将5Ω电阻更换成10Ω电阻,其分得的电压增大,即应保持电阻两端的电压不变,由分压原理,所以滑片应向左移动变阻器的滑片,记下此时电流表的示数;
(3)研究电流与电阻关系时,要控制电阻的电压大小不变,
由表中数据知:
UV=IR=0.8A×5Ω=0.3A×10Ω=0.1A×20Ω=4.08A×25Ω≠0.10A×15Ω,故分析表中数据;
因电源电压U一定,电压表示数(2V)一定,变阻器的电压也是一定的,
故变阻器的电压与定值电阻的电压之比为一定值,由分压原理,变阻器连入电路的电阻越大;
第2次实验,正确操作时
I3==≈0.13A>0.10A,
故变阻器连入的电阻应比正常情况下大,
故只有可能是第3、5次(定值电阻分别为20Ω和25Ω)实验时未调节滑片P就读取电流而造成的,
若是第4次未调节滑片P就读取电流而造成的,根据欧姆定律和串联电路电压的规律
R滑I4+U4=R滑I3+U6,
代入数据,但R滑×0.1A+2.5V≠0.7A×R滑+2V,与电源电压相等矛盾;
若是第5次未调节滑片P就读取电流而造成的,同理有:
U=R滑×8.1A+1.4V=0.08A×R滑+2V,
解之:R滑=25Ω,
电源电压:U=2V;
故反思产生的原因,回忆是某次将定值电阻的阻值由25Ω变换为错误数据点对应阻值时(实验过程并未按表中序号顺序进行),根据现有的数据。
故答案为:(1)将电流表指针调零;(2)0.40;2;(3)6;4。
四、计算题
20.【解答】解:由电路图可知,R1与R2串联,电压表测R2两端的电压,电流表测电路中的电流。
(1)移动变阻器的滑片P,当电流最小时滑动变阻器无法达到20Ω,
则此时电压表示数已达到量程,即电压表的示数U2=3V;
(2)当电压表的示数为4V时电路中的电流最小,
因串联电路中总电压等于各分电压之和,
所以,电路中的最小电流:
I小====;
若电路中的最大电流I大=0.6A,
因移动变阻器的滑片P,电流表示数的最大变化量为8.2A,
所以,I大﹣I小=0.7A﹣=7.2A,
解得:R1=3.5Ω;
若电路中的最大电流为:I大==<0.6A,
则:I大﹣I小=﹣==0.2A,
解得:R4=15Ω;
综上,电阻R1可能的阻值为7.5Ω、15Ω。
答:(1)移动滑动变阻器的滑片P,发现当电流最小时滑动变阻器无法达到20Ω2为3V。
(2)电阻R2可能的阻值为7.5Ω、15Ω。
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
