18.1.1平行四边形的性质(第1课时)
文档属性
| 名称 | 18.1.1平行四边形的性质(第1课时) |  | |
| 格式 | zip | ||
| 文件大小 | 746.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 09:09:56 | ||
图片预览







文档简介
课件21张PPT。数 学新课标(RJ) 八年级下册第十八章 平行四边形 18.1 平行四边形18.1.1 平行四边形的性质第1课时 平行四边形的性质(1)第1课时 平行四边形的性质(1) 教材【第42页例1】改编题
如图18-1-1所示,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:AE=CF;
(2)若∠A=60°,AD=4,AB=7,求?ABCD的面积.图18-1-1第1课时 平行四边形的性质(1)解:(1)证明:方法一:∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB.
又∵∠AED=∠CFB=90°,∴△ADE≌△CBF,∴AE=CF.
方法二:∵四边形ABCD是平行四边形,∴AB∥CD,AD=CB.
又∵DE⊥AB,BF⊥CD,∴∠AED=∠CFB=90°,DE∥BF,
∴DE=BF(平行线间的平行线段相等),
∴△ADE≌△CBF(HL),∴AE=CF.第1课时 平行四边形的性质(1)方法三:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴DF∥EB.
又∵DE⊥AB,BF⊥CD,∴DE∥BF,
∴四边形DEBF是平行四边形,∴EB=FD.
∵AE=AB-EB,CF=CD-FD,∴AE=CF.第1课时 平行四边形的性质(1) ? 活动1 知识准备第1课时 平行四边形的性质(1)1.四边形的内角和为_______________.
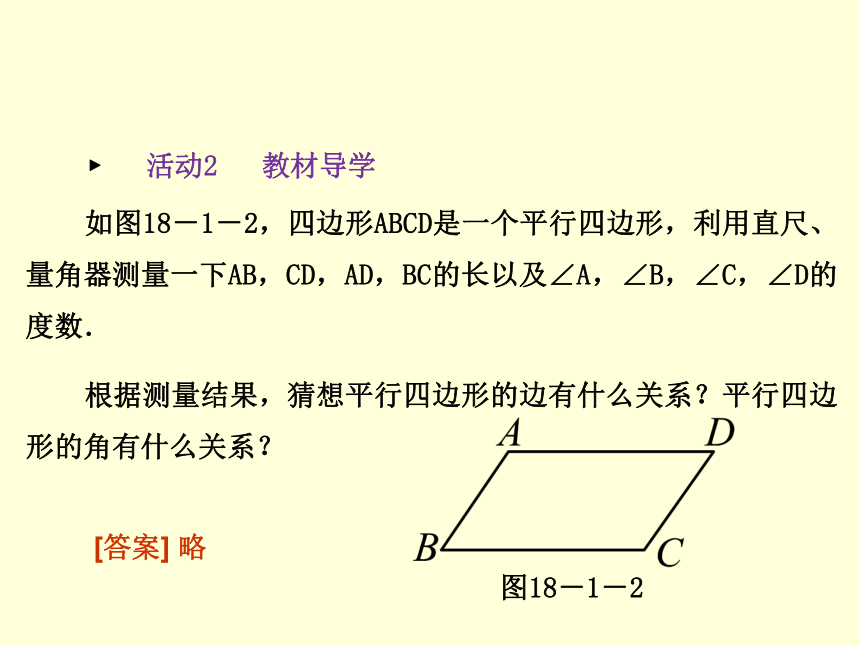
2.在小学,学过一些特殊的四边形,它们是__________、___________、________________和____________.360°长方形正方形平行四边形梯形 ? 活动2 教材导学 第1课时 平行四边形的性质(1)如图18-1-2,四边形ABCD是一个平行四边形,利用直尺、量角器测量一下AB,CD,AD,BC的长以及∠A,∠B,∠C,∠D的度数.
根据测量结果,猜想平行四边形的边有什么关系?平行四边形的角有什么关系?图18-1-2[答案] 略 ? 知识点一 平行四边形的概念及表示 第1课时 平行四边形的性质(1)定义:两组对边分别________的四边形叫做平行四边形.
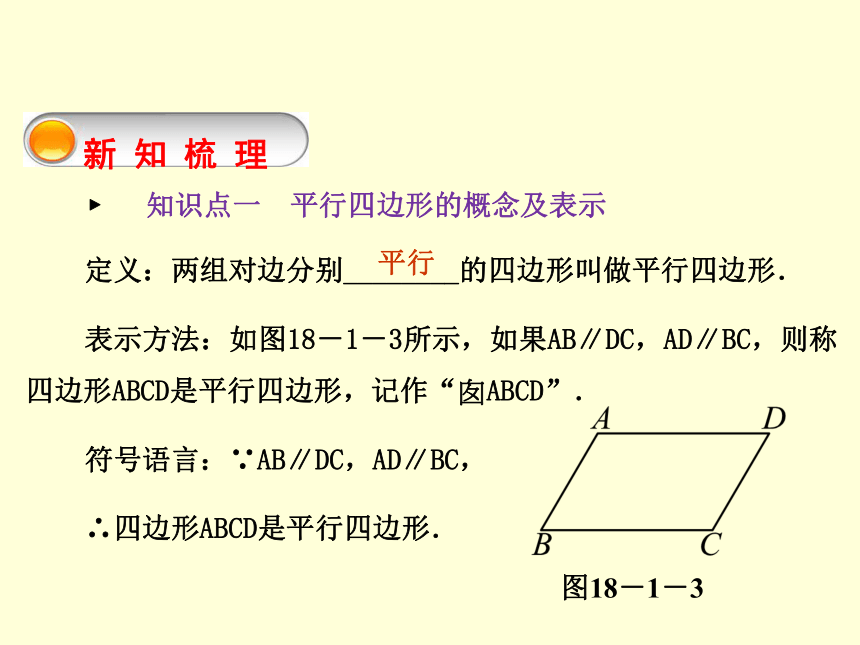
表示方法:如图18-1-3所示,如果AB∥DC,AD∥BC,则称四边形ABCD是平行四边形,记作“?ABCD”.
符号语言:∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形.平行图18-1-3第1课时 平行四边形的性质(1) ? 知识点二 平行四边形有关边和角的性质定理 性质1:平行四边形的对边________.
符号语言:∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC.
性质2:平行四边形的________相等.
符号语言:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D.相等对角第1课时 平行四边形的性质(1) ? 知识点三 两条平行线之间的距离 定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.如图18-1-4,a∥b,A是a上的任意一点,AB⊥b,B是垂足,线段AB的长就是a,b之间的距离.图18-1-4性质:两条平行线间的距离处处相等. 探究问题一 平行四边形边角性质的简单应用 第1课时 平行四边形的性质(1)CB第1课时 平行四边形的性质(1)[解析] (1)C 在?ABCD中,∠A+∠B=180°,∠A=∠C.又因为∠A+∠C=200°,所以∠A=100°,所以∠B=180°-∠A=80°.
(2)B 在?ABCD中,AD∥BC,所以∠DEC=∠ECB.又因为CE平分∠BCD,所以∠DCE=∠BCE,所以∠DCE=∠DEC,所以DC=DE.因为AB=CD,AD=2AB,所以AD=AE+DE=AE+AB=2AB,而AE=3,所以AB=3.第1课时 平行四边形的性质(1)[归纳总结] 平行四边形的性质中存在着线段、角之间的数量关系,可以证明线段相等、角相等或进行线段、角的计算,另外,还可以用以列方程,从而巧妙地解决有关问题. 第1课时 平行四边形的性质(1)探究问题二 平行线间距离的应用 例2 如图18-1-6,在?ABCD中,点E在边AD上,连接AC,BE,EC.
求证:S△ABC=S△EBC.图18-1-6第1课时 平行四边形的性质(1)[解析] 根据“两平行线间的距离处处相等”可得△ABC与△EBC在BC边上的高相等,再根据“同底等高的三角形的面积相等”得到结论.
证明:分别过点A,E作AF⊥BC于点F,EG⊥BC于点G.∵四边形ABCD是平行四边形,∴AD∥BC.又由作法知AF和EG分别是AD上的点A,E到直线BC的距离,∴AF=EG(两平行线间的距离处处相等),∴S△ABC=S△EBC(同底等高的两个三角形的面积相等).第1课时 平行四边形的性质(1)[归纳总结] 两平行线间的距离相等是两平行线间的平行线段相等的特例,因为两平行线与它们之间的平行线段形成平行四边形.第1课时 平行四边形的性质(1)探究问题三 平行四边形边、角性质的综合运用 例3 如图18-1-7所示,在?ABCD中,∠BAD=32°,分别以BC,CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E,C两点之间,连接AE,AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数. 图18-1-7第1课时 平行四边形的性质(1)[解析] (1)利用平行四边形对角相等证∠ADF=∠ABE,再利用平行四边形对边相等证夹上述两角的两边对应相等.
(2)利用全等三角形的对应角相等,将其转化为求∠EAB+∠FAD的度数.第1课时 平行四边形的性质(1)解:(1)证明:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD=BC=BE,DF=DC=AB.
在△ABE和△FDA中,AB=FD,BE=DA,
∠ABE=360°-∠ABC-∠EBC=360°-∠ADC-∠CDF=∠ADF,
∴△ABE≌△FDA(SAS).
(2)由(1)得∠AEB=∠FAD,∴∠EBH=∠AEB+∠EAB=∠EAB+∠FAD=90°-∠BAD=90°-32°=58°,即∠EBH=58°.第1课时 平行四边形的性质(1)[归纳总结] (1)平行四边形对边相等、对角相等的性质,常常为我们提供证明两个三角形全等边角相等的条件.
(2)对于四边形的问题,我们常常把它转化为三角形的问题来解决,平行四边形也是如此.
如图18-1-1所示,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.
(1)求证:AE=CF;
(2)若∠A=60°,AD=4,AB=7,求?ABCD的面积.图18-1-1第1课时 平行四边形的性质(1)解:(1)证明:方法一:∵四边形ABCD是平行四边形,∴∠A=∠C,AD=CB.
又∵∠AED=∠CFB=90°,∴△ADE≌△CBF,∴AE=CF.
方法二:∵四边形ABCD是平行四边形,∴AB∥CD,AD=CB.
又∵DE⊥AB,BF⊥CD,∴∠AED=∠CFB=90°,DE∥BF,
∴DE=BF(平行线间的平行线段相等),
∴△ADE≌△CBF(HL),∴AE=CF.第1课时 平行四边形的性质(1)方法三:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴DF∥EB.
又∵DE⊥AB,BF⊥CD,∴DE∥BF,
∴四边形DEBF是平行四边形,∴EB=FD.
∵AE=AB-EB,CF=CD-FD,∴AE=CF.第1课时 平行四边形的性质(1) ? 活动1 知识准备第1课时 平行四边形的性质(1)1.四边形的内角和为_______________.
2.在小学,学过一些特殊的四边形,它们是__________、___________、________________和____________.360°长方形正方形平行四边形梯形 ? 活动2 教材导学 第1课时 平行四边形的性质(1)如图18-1-2,四边形ABCD是一个平行四边形,利用直尺、量角器测量一下AB,CD,AD,BC的长以及∠A,∠B,∠C,∠D的度数.
根据测量结果,猜想平行四边形的边有什么关系?平行四边形的角有什么关系?图18-1-2[答案] 略 ? 知识点一 平行四边形的概念及表示 第1课时 平行四边形的性质(1)定义:两组对边分别________的四边形叫做平行四边形.
表示方法:如图18-1-3所示,如果AB∥DC,AD∥BC,则称四边形ABCD是平行四边形,记作“?ABCD”.
符号语言:∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形.平行图18-1-3第1课时 平行四边形的性质(1) ? 知识点二 平行四边形有关边和角的性质定理 性质1:平行四边形的对边________.
符号语言:∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC.
性质2:平行四边形的________相等.
符号语言:∵四边形ABCD是平行四边形,
∴∠A=∠C,∠B=∠D.相等对角第1课时 平行四边形的性质(1) ? 知识点三 两条平行线之间的距离 定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.如图18-1-4,a∥b,A是a上的任意一点,AB⊥b,B是垂足,线段AB的长就是a,b之间的距离.图18-1-4性质:两条平行线间的距离处处相等. 探究问题一 平行四边形边角性质的简单应用 第1课时 平行四边形的性质(1)CB第1课时 平行四边形的性质(1)[解析] (1)C 在?ABCD中,∠A+∠B=180°,∠A=∠C.又因为∠A+∠C=200°,所以∠A=100°,所以∠B=180°-∠A=80°.
(2)B 在?ABCD中,AD∥BC,所以∠DEC=∠ECB.又因为CE平分∠BCD,所以∠DCE=∠BCE,所以∠DCE=∠DEC,所以DC=DE.因为AB=CD,AD=2AB,所以AD=AE+DE=AE+AB=2AB,而AE=3,所以AB=3.第1课时 平行四边形的性质(1)[归纳总结] 平行四边形的性质中存在着线段、角之间的数量关系,可以证明线段相等、角相等或进行线段、角的计算,另外,还可以用以列方程,从而巧妙地解决有关问题. 第1课时 平行四边形的性质(1)探究问题二 平行线间距离的应用 例2 如图18-1-6,在?ABCD中,点E在边AD上,连接AC,BE,EC.
求证:S△ABC=S△EBC.图18-1-6第1课时 平行四边形的性质(1)[解析] 根据“两平行线间的距离处处相等”可得△ABC与△EBC在BC边上的高相等,再根据“同底等高的三角形的面积相等”得到结论.
证明:分别过点A,E作AF⊥BC于点F,EG⊥BC于点G.∵四边形ABCD是平行四边形,∴AD∥BC.又由作法知AF和EG分别是AD上的点A,E到直线BC的距离,∴AF=EG(两平行线间的距离处处相等),∴S△ABC=S△EBC(同底等高的两个三角形的面积相等).第1课时 平行四边形的性质(1)[归纳总结] 两平行线间的距离相等是两平行线间的平行线段相等的特例,因为两平行线与它们之间的平行线段形成平行四边形.第1课时 平行四边形的性质(1)探究问题三 平行四边形边、角性质的综合运用 例3 如图18-1-7所示,在?ABCD中,∠BAD=32°,分别以BC,CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF.延长AB交边EC于点H,点H在E,C两点之间,连接AE,AF.
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBH的度数. 图18-1-7第1课时 平行四边形的性质(1)[解析] (1)利用平行四边形对角相等证∠ADF=∠ABE,再利用平行四边形对边相等证夹上述两角的两边对应相等.
(2)利用全等三角形的对应角相等,将其转化为求∠EAB+∠FAD的度数.第1课时 平行四边形的性质(1)解:(1)证明:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,AD=BC=BE,DF=DC=AB.
在△ABE和△FDA中,AB=FD,BE=DA,
∠ABE=360°-∠ABC-∠EBC=360°-∠ADC-∠CDF=∠ADF,
∴△ABE≌△FDA(SAS).
(2)由(1)得∠AEB=∠FAD,∴∠EBH=∠AEB+∠EAB=∠EAB+∠FAD=90°-∠BAD=90°-32°=58°,即∠EBH=58°.第1课时 平行四边形的性质(1)[归纳总结] (1)平行四边形对边相等、对角相等的性质,常常为我们提供证明两个三角形全等边角相等的条件.
(2)对于四边形的问题,我们常常把它转化为三角形的问题来解决,平行四边形也是如此.
