18.1.2平行四边形的判定(第1课时)
文档属性
| 名称 | 18.1.2平行四边形的判定(第1课时) |  | |
| 格式 | zip | ||
| 文件大小 | 714.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 09:09:37 | ||
图片预览







文档简介
课件35张PPT。数 学新课标(RJ) 八年级下册第十八章 平行四边形 18.1 平行四边形18.1.2 平行四边形的判定第1课时 平行四边形的判定(1)第1课时 平行四边形的判定(1)教材重难处理 教材【第46页例3】改编题
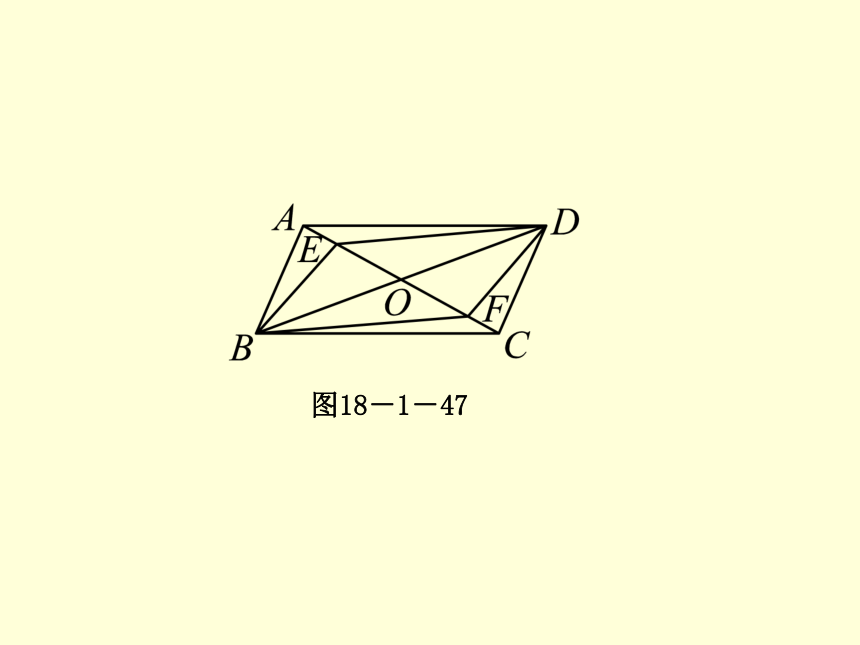
如图18-1-47所示,?ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.
(1)线段BE,DF有怎样的数量关系和位置关系?请说明理由;
(2)线段BF,DE有怎样的数量关系和位置关系?请说明理由;
(3)求证:四边形BFDE是平行四边形.第1课时 平行四边形的判定(1)图18-1-47第1课时 平行四边形的判定(1)[解析] 由平行四边形的性质可得,AO=CO,BO=DO,AB=CD,AB∥CD,AD=CB,AD∥CB.又由AB∥CD可得,∠BAE=∠DCF.由AD∥CB可得,∠DAE=∠BCF,再结合已知条件AE=CF可证得△ABE≌△CDF,△ADE≌△CBF,EO=FO,由全等三角形的性质可得,BE=DF,DE=BF,∠AEB=∠CFD,∠AED=∠CFB,再根据等角的补角相等可得,∠BEO=∠DFO,∠DEO=∠BFO,由此可得,BE∥DF,DE∥BF.有了前面的推理,目前自然就有三种方法“两组对边分别平行、两组对边分别相等和对角线互相平分”证明四边形BFDE是平行四边形.第1课时 平行四边形的判定(1)解:(1)BE=DF,BE∥DF.理由如下:
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,
∴∠BAE=∠DCF.又∵AE=CF,∴△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD.
又∵∠AEB+∠BEO=180°,∠CFD+∠DFO=180°,
∴∠BEO=∠DFO,∴BE∥DF.
(2)BF=DE,BF∥DE.理由略(过程推理类似(1)).第1课时 平行四边形的判定(1)(3)证明:方法一:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO.∵AE=CF,∴AO-AE=CO-CF,即EO=FO.又∵BO=DO,∴四边形BFDE是平行四边形.
方法二:由(1),(2)有BE∥DF,DE∥BF,∴四边形BFDE是平行四边形.
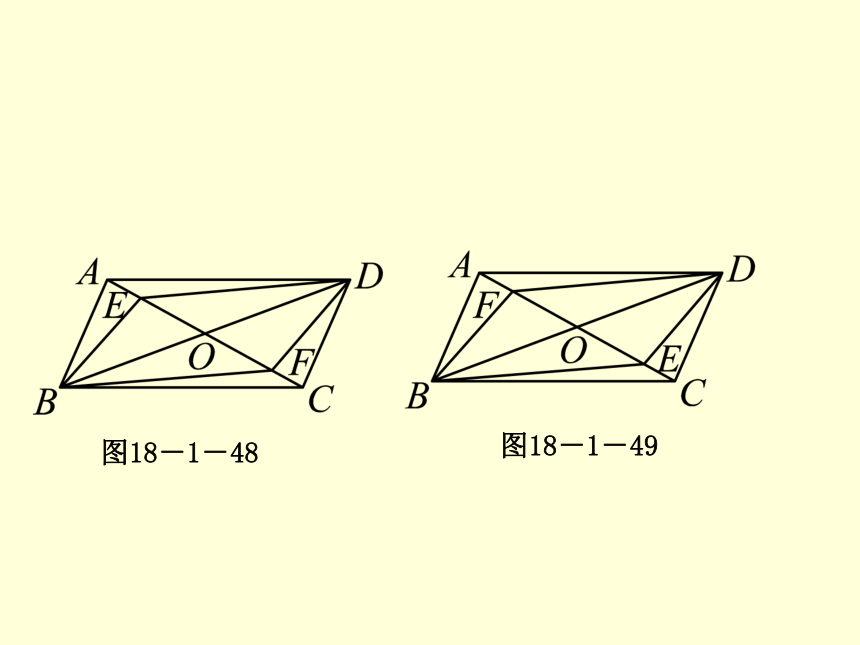
方法三:由(1),(2)有BE=DF,DE=BF,∴四边形BFDE是平行四边形.第1课时 平行四边形的判定(1)变式1 如图18-1-48,当点E,F是线段AC上的两动点,且在运动时始终有AE=CF,其他条件不变,改编题中的结论还成立吗?为什么?
解:应分三种情况,其中一种就是改编题的情形.第二种是当点E,O,F三点重合时,显然只有(1),(2)中的相等关系成立,其他均不成立.第三种情形如图18-1-49所示,同改编题思路及分析,此时结论都成立.第1课时 平行四边形的判定(1)图18-1-48
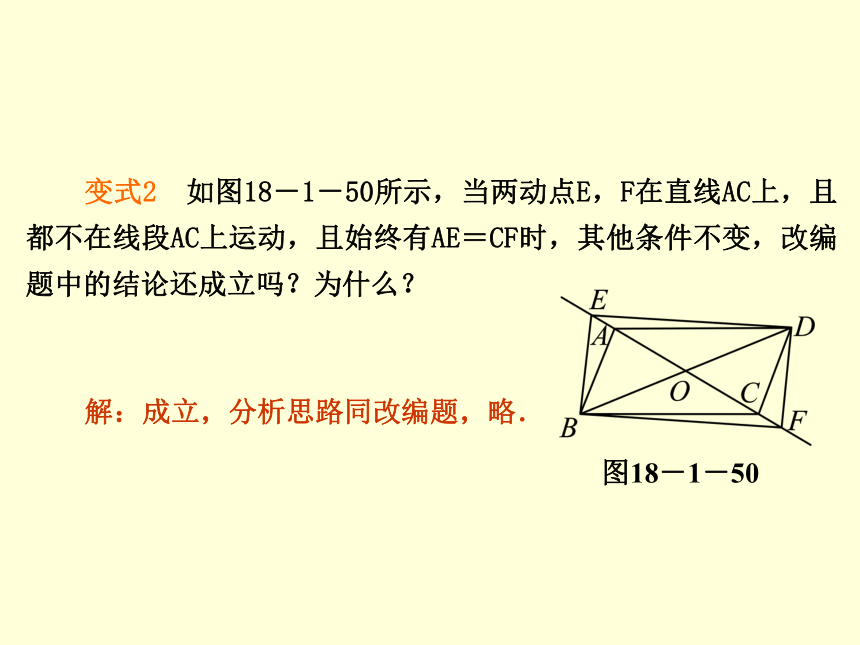
图18-1-49第1课时 平行四边形的判定(1)变式2 如图18-1-50所示,当两动点E,F在直线AC上,且都不在线段AC上运动,且始终有AE=CF时,其他条件不变,改编题中的结论还成立吗?为什么?
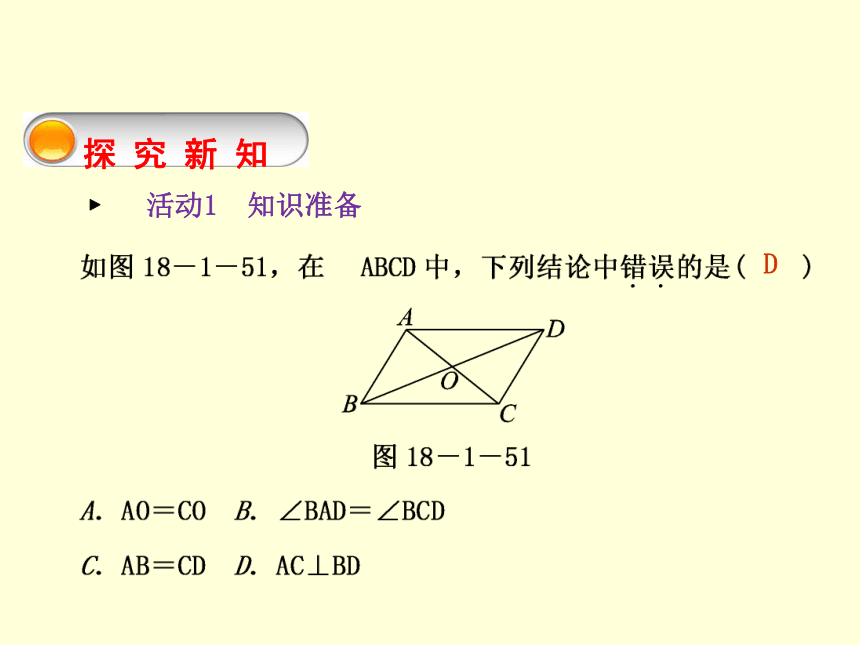
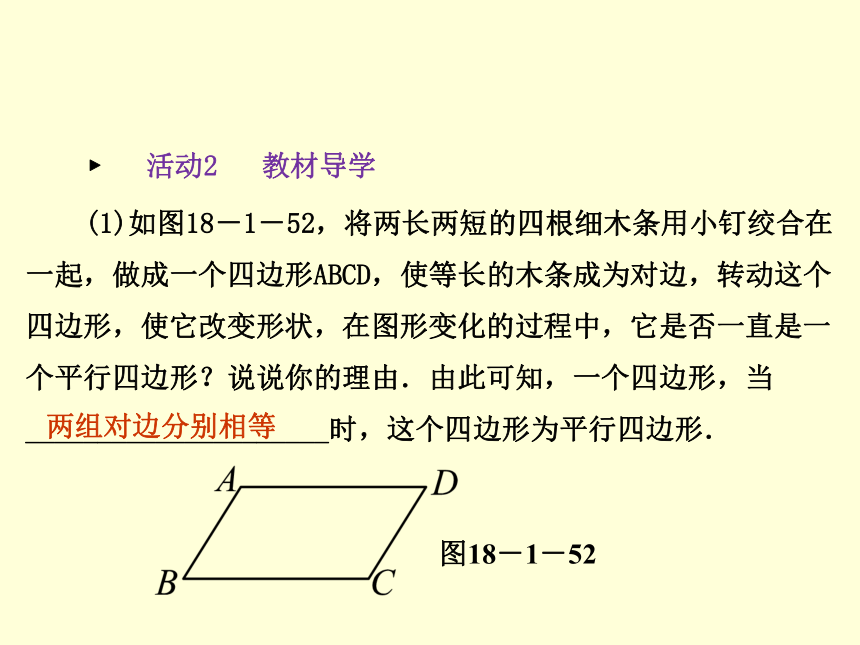
解:成立,分析思路同改编题,略. 图18-1-50 探 究 新 知 ? 活动1 知识准备第1课时 平行四边形的判定(1)D ? 活动2 教材导学 第1课时 平行四边形的判定(1)(1)如图18-1-52,将两长两短的四根细木条用小钉绞合在一起,做成一个四边形ABCD,使等长的木条成为对边,转动这个四边形,使它改变形状,在图形变化的过程中,它是否一直是一个平行四边形?说说你的理由.由此可知,一个四边形,当_____________________时,这个四边形为平行四边形.图18-1-52两组对边分别相等第1课时 平行四边形的判定(1)[答案] 四边形ABCD一直是一个平行四边形.理由如下:
如图18-1-53,连接AC.∵AB=CD,AD=CB,AC=CA,∴△ABC≌△CDA,
∴∠1=∠2,∠3=∠4,∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.图18-1-53第1课时 平行四边形的判定(1)◆链接知识——[新知梳理]知识点一
(2)我们知道平行四边形的对角相等,那么对角相等的四边形一定是平行四边形吗?图18-1-54第1课时 平行四边形的判定(1)如图18-1-54所示,在四边形ABCD中,如果∠A=∠C,∠B=∠D,四边形ABCD一定是平行四边形吗?说说你的理由.由此可知,一个四边形,当_________________时,这个四边形为平行四边形.两组对角分别相等图18-1-54第1课时 平行四边形的判定(1)[答案] 四边形ABCD一定是一个平行四边形.理由如下:
∵∠A=∠C,∠B=∠D,∠A+∠C+∠B+∠D=360°,∴∠A+∠B=180°,∠A+∠D=180°,
∴AD∥BC,AB∥CD,∴四边形ABCD是平行四边形.第1课时 平行四边形的判定(1)◆链接知识——[新知梳理]知识点二
(3)如图18-1-55,将两根细木条AC,BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两个木条,四边形ABCD一直是一个平行四边形吗?说说你的理由.由此可知,一个四边形,当两条对角线互相平分 时,这个四边形为平行四边形. 图18-1-55第1课时 平行四边形的判定(1)[答案] 四边形ABCD一直是一个平行四边形.理由如下:
∵AO=CO,∠AOD=∠COB,DO=BO,
∴△AOD≌△COB,∴AD=BC.同理AB=DC,
∴四边形ABCD是平行四边形.新 知 梳 理 ? 知识点一 由对边的数量关系判定平行四边形 第1课时 平行四边形的判定(1)定理1:两组对边分别___________的四边形是平行四边形.
符号语言:如图18-1-56所示,在四边形ABCD中,图18-1-56相等第1课时 平行四边形的判定(1)∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
[注意] (1)平行四边形的概念实际上是从两组边的位置关系(平行)来判定一个四边形是平行四边形的,所以按照四边形对边的数量关系和位置关系均能判定它是否是平行四边形;(2)平行四边形的性质定理和判定定理为互逆定理.第1课时 平行四边形的判定(1) ? 知识点二 由对角的数量关系判定平行四边形 定理2:两组对角分别__________的四边形是平行四边形.
符号语言:如图18-1-57所示,
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
[说明] 从邻角的关系也能判定一个四边形是否是平行四边形.如果四边形的一个内角与它的两个邻角都互补,那么这个四边形是平行四边形.相等第1课时 平行四边形的判定(1)图18-1-57第1课时 平行四边形的判定(1) ? 知识点三 由对角线的平分关系判定平行四边形 定理3:对角线_____________的四边形是平行四边形.
符号语言:如图18-1-58所示,在四边形ABCD中,对角线AC,BD相交于点O.
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形.图18-1-58 互相平分重难互动探究探究问题一 由对角的数量关系判定平行四边形 第1课时 平行四边形的判定(1)例1 已知:如图18-1-59,在四边形ABCD中,AD∥BC,∠A=∠C.求证:四边形ABCD是平行四边形. 图18-1-59第1课时 平行四边形的判定(1)[解析] 方法一:已知一组对边平行,可以通过证明另一组对边也平行,利用定义证明四边形是平行四边形.(同学们自己完成证明)
方法二:已知四边形的一组对角相等,可以通过证明另一组对角也相等,从而证明四边形是平行四边形.第1课时 平行四边形的判定(1)证明: (方法二)∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°.
∵∠A=∠C,∴∠B=∠D,
∴四边形ABCD是平行四边形.
[归纳总结] 平行四边形的两组对角分别相等,反之,利用一个四边形两组对角的这种数量关系也可以来证明一个四边形是平行四边形.延伸下去,可以得到两组对边平行的位置关系和两组对边分别相等的数量关系,完成由角的条件到边的条件的转化.第1课时 平行四边形的判定(1)探究问题二 由对边的数量关系判定平行四边形 例2 如图18-1-60,点E,F是?ABCD的对角线AC上的两点,且AE=CF.
求证:四边形DEBF是平行四边形. 图18-1-60第1课时 平行四边形的判定(1)[解析] 已知AE=CF,结合四边形ABCD是平行四边形可通过证明△ADE≌△CBF得到DE=BF,由△ABE≌△CDF得到BE=DF,运用两组对边分别相等的四边形是平行四边形来证明.第1课时 平行四边形的判定(1)第1课时 平行四边形的判定(1)第1课时 平行四边形的判定(1)[归纳总结] 平行四边形的两组对边分别相等,反之,利用四边形两组对边的这种数量关系也可以来证明一个四边形是平行四边形.如果延伸下去,可以得到两组对边的平行,从而通过对边的数量关系,得出对边的位置关系.第1课时 平行四边形的判定(1)探究问题三 由对角线的平分关系判定平行四边形 例3 如图18-1-61,过?ABCD的对角线的交点O作直线EF,分别交AD于点E,交BC于点F,G,H分别为OD,OB的中点.求证:四边形EHFG是平行四边形.图18-1-61第1课时 平行四边形的判定(1)[解析] 所证四边形EHFG中两条对角线交于点O,且OG=OH,为此只需证明OE=OF即可,由已知条件可证△AOE≌△COF.第1课时 平行四边形的判定(1)第1课时 平行四边形的判定(1)[归纳总结] 若所证四边形中有对角线出现或原已知四边形中出现了对角线的,则用“对角线互相平分的四边形是平行四边形”这一定理解决问题最为简便.
如图18-1-47所示,?ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.
(1)线段BE,DF有怎样的数量关系和位置关系?请说明理由;
(2)线段BF,DE有怎样的数量关系和位置关系?请说明理由;
(3)求证:四边形BFDE是平行四边形.第1课时 平行四边形的判定(1)图18-1-47第1课时 平行四边形的判定(1)[解析] 由平行四边形的性质可得,AO=CO,BO=DO,AB=CD,AB∥CD,AD=CB,AD∥CB.又由AB∥CD可得,∠BAE=∠DCF.由AD∥CB可得,∠DAE=∠BCF,再结合已知条件AE=CF可证得△ABE≌△CDF,△ADE≌△CBF,EO=FO,由全等三角形的性质可得,BE=DF,DE=BF,∠AEB=∠CFD,∠AED=∠CFB,再根据等角的补角相等可得,∠BEO=∠DFO,∠DEO=∠BFO,由此可得,BE∥DF,DE∥BF.有了前面的推理,目前自然就有三种方法“两组对边分别平行、两组对边分别相等和对角线互相平分”证明四边形BFDE是平行四边形.第1课时 平行四边形的判定(1)解:(1)BE=DF,BE∥DF.理由如下:
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,
∴∠BAE=∠DCF.又∵AE=CF,∴△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD.
又∵∠AEB+∠BEO=180°,∠CFD+∠DFO=180°,
∴∠BEO=∠DFO,∴BE∥DF.
(2)BF=DE,BF∥DE.理由略(过程推理类似(1)).第1课时 平行四边形的判定(1)(3)证明:方法一:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO.∵AE=CF,∴AO-AE=CO-CF,即EO=FO.又∵BO=DO,∴四边形BFDE是平行四边形.
方法二:由(1),(2)有BE∥DF,DE∥BF,∴四边形BFDE是平行四边形.
方法三:由(1),(2)有BE=DF,DE=BF,∴四边形BFDE是平行四边形.第1课时 平行四边形的判定(1)变式1 如图18-1-48,当点E,F是线段AC上的两动点,且在运动时始终有AE=CF,其他条件不变,改编题中的结论还成立吗?为什么?
解:应分三种情况,其中一种就是改编题的情形.第二种是当点E,O,F三点重合时,显然只有(1),(2)中的相等关系成立,其他均不成立.第三种情形如图18-1-49所示,同改编题思路及分析,此时结论都成立.第1课时 平行四边形的判定(1)图18-1-48
图18-1-49第1课时 平行四边形的判定(1)变式2 如图18-1-50所示,当两动点E,F在直线AC上,且都不在线段AC上运动,且始终有AE=CF时,其他条件不变,改编题中的结论还成立吗?为什么?
解:成立,分析思路同改编题,略. 图18-1-50 探 究 新 知 ? 活动1 知识准备第1课时 平行四边形的判定(1)D ? 活动2 教材导学 第1课时 平行四边形的判定(1)(1)如图18-1-52,将两长两短的四根细木条用小钉绞合在一起,做成一个四边形ABCD,使等长的木条成为对边,转动这个四边形,使它改变形状,在图形变化的过程中,它是否一直是一个平行四边形?说说你的理由.由此可知,一个四边形,当_____________________时,这个四边形为平行四边形.图18-1-52两组对边分别相等第1课时 平行四边形的判定(1)[答案] 四边形ABCD一直是一个平行四边形.理由如下:
如图18-1-53,连接AC.∵AB=CD,AD=CB,AC=CA,∴△ABC≌△CDA,
∴∠1=∠2,∠3=∠4,∴AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.图18-1-53第1课时 平行四边形的判定(1)◆链接知识——[新知梳理]知识点一
(2)我们知道平行四边形的对角相等,那么对角相等的四边形一定是平行四边形吗?图18-1-54第1课时 平行四边形的判定(1)如图18-1-54所示,在四边形ABCD中,如果∠A=∠C,∠B=∠D,四边形ABCD一定是平行四边形吗?说说你的理由.由此可知,一个四边形,当_________________时,这个四边形为平行四边形.两组对角分别相等图18-1-54第1课时 平行四边形的判定(1)[答案] 四边形ABCD一定是一个平行四边形.理由如下:
∵∠A=∠C,∠B=∠D,∠A+∠C+∠B+∠D=360°,∴∠A+∠B=180°,∠A+∠D=180°,
∴AD∥BC,AB∥CD,∴四边形ABCD是平行四边形.第1课时 平行四边形的判定(1)◆链接知识——[新知梳理]知识点二
(3)如图18-1-55,将两根细木条AC,BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD.转动两个木条,四边形ABCD一直是一个平行四边形吗?说说你的理由.由此可知,一个四边形,当两条对角线互相平分 时,这个四边形为平行四边形. 图18-1-55第1课时 平行四边形的判定(1)[答案] 四边形ABCD一直是一个平行四边形.理由如下:
∵AO=CO,∠AOD=∠COB,DO=BO,
∴△AOD≌△COB,∴AD=BC.同理AB=DC,
∴四边形ABCD是平行四边形.新 知 梳 理 ? 知识点一 由对边的数量关系判定平行四边形 第1课时 平行四边形的判定(1)定理1:两组对边分别___________的四边形是平行四边形.
符号语言:如图18-1-56所示,在四边形ABCD中,图18-1-56相等第1课时 平行四边形的判定(1)∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
[注意] (1)平行四边形的概念实际上是从两组边的位置关系(平行)来判定一个四边形是平行四边形的,所以按照四边形对边的数量关系和位置关系均能判定它是否是平行四边形;(2)平行四边形的性质定理和判定定理为互逆定理.第1课时 平行四边形的判定(1) ? 知识点二 由对角的数量关系判定平行四边形 定理2:两组对角分别__________的四边形是平行四边形.
符号语言:如图18-1-57所示,
在四边形ABCD中,∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
[说明] 从邻角的关系也能判定一个四边形是否是平行四边形.如果四边形的一个内角与它的两个邻角都互补,那么这个四边形是平行四边形.相等第1课时 平行四边形的判定(1)图18-1-57第1课时 平行四边形的判定(1) ? 知识点三 由对角线的平分关系判定平行四边形 定理3:对角线_____________的四边形是平行四边形.
符号语言:如图18-1-58所示,在四边形ABCD中,对角线AC,BD相交于点O.
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形.图18-1-58 互相平分重难互动探究探究问题一 由对角的数量关系判定平行四边形 第1课时 平行四边形的判定(1)例1 已知:如图18-1-59,在四边形ABCD中,AD∥BC,∠A=∠C.求证:四边形ABCD是平行四边形. 图18-1-59第1课时 平行四边形的判定(1)[解析] 方法一:已知一组对边平行,可以通过证明另一组对边也平行,利用定义证明四边形是平行四边形.(同学们自己完成证明)
方法二:已知四边形的一组对角相等,可以通过证明另一组对角也相等,从而证明四边形是平行四边形.第1课时 平行四边形的判定(1)证明: (方法二)∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°.
∵∠A=∠C,∴∠B=∠D,
∴四边形ABCD是平行四边形.
[归纳总结] 平行四边形的两组对角分别相等,反之,利用一个四边形两组对角的这种数量关系也可以来证明一个四边形是平行四边形.延伸下去,可以得到两组对边平行的位置关系和两组对边分别相等的数量关系,完成由角的条件到边的条件的转化.第1课时 平行四边形的判定(1)探究问题二 由对边的数量关系判定平行四边形 例2 如图18-1-60,点E,F是?ABCD的对角线AC上的两点,且AE=CF.
求证:四边形DEBF是平行四边形. 图18-1-60第1课时 平行四边形的判定(1)[解析] 已知AE=CF,结合四边形ABCD是平行四边形可通过证明△ADE≌△CBF得到DE=BF,由△ABE≌△CDF得到BE=DF,运用两组对边分别相等的四边形是平行四边形来证明.第1课时 平行四边形的判定(1)第1课时 平行四边形的判定(1)第1课时 平行四边形的判定(1)[归纳总结] 平行四边形的两组对边分别相等,反之,利用四边形两组对边的这种数量关系也可以来证明一个四边形是平行四边形.如果延伸下去,可以得到两组对边的平行,从而通过对边的数量关系,得出对边的位置关系.第1课时 平行四边形的判定(1)探究问题三 由对角线的平分关系判定平行四边形 例3 如图18-1-61,过?ABCD的对角线的交点O作直线EF,分别交AD于点E,交BC于点F,G,H分别为OD,OB的中点.求证:四边形EHFG是平行四边形.图18-1-61第1课时 平行四边形的判定(1)[解析] 所证四边形EHFG中两条对角线交于点O,且OG=OH,为此只需证明OE=OF即可,由已知条件可证△AOE≌△COF.第1课时 平行四边形的判定(1)第1课时 平行四边形的判定(1)[归纳总结] 若所证四边形中有对角线出现或原已知四边形中出现了对角线的,则用“对角线互相平分的四边形是平行四边形”这一定理解决问题最为简便.
