18.1.2 平行四边形的判定(第2课时)
文档属性
| 名称 | 18.1.2 平行四边形的判定(第2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 750.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 00:00:00 | ||
图片预览






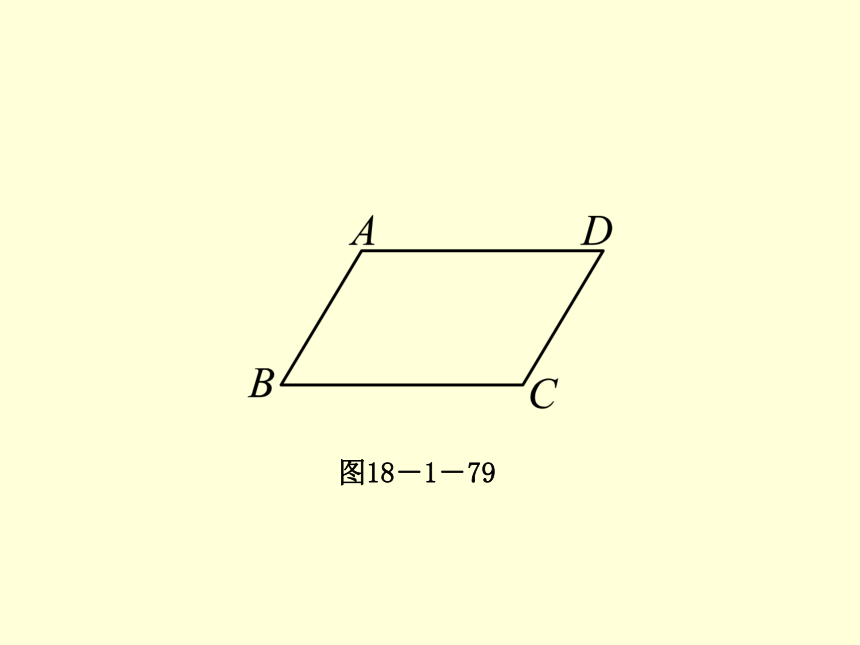
文档简介
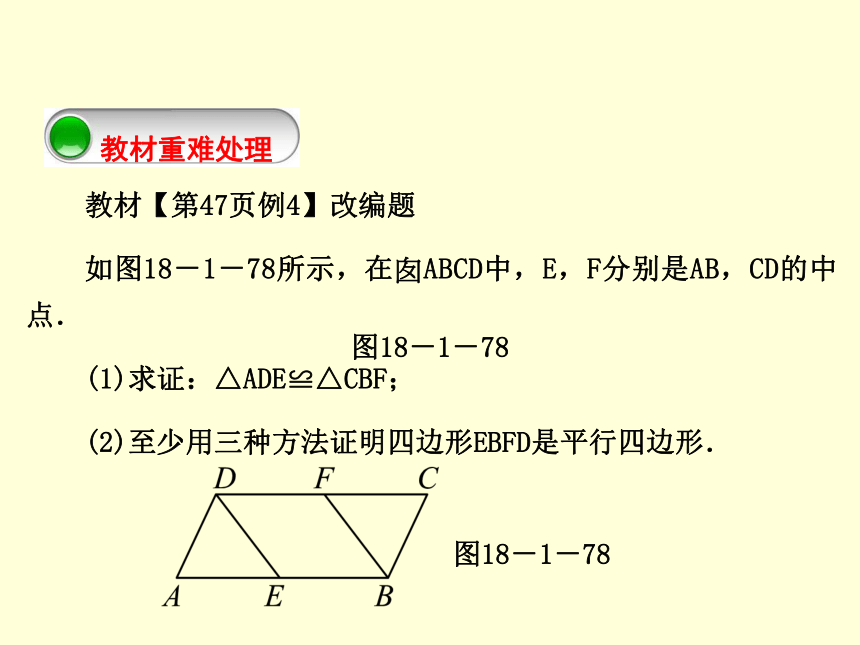
课件22张PPT。数 学新课标(RJ) 八年级下册第十八章 平行四边形 18.1 平行四边形18.1.2 平行四边形的判定第2课时 平行四边形的判定(2)第2课时 平行四边形的判定(2)教材【第47页例4】改编题
如图18-1-78所示,在?ABCD中,E,F分别是AB,CD的中点.
(1)求证:△ADE≌△CBF;
(2)至少用三种方法证明四边形EBFD是平行四边形.图18-1-78图18-1-78第2课时 平行四边形的判定(2)第2课时 平行四边形的判定(2)第2课时 平行四边形的判定(2)方法三:∵四边形ABCD是平行四边形,∴∠ADC=∠CBA.
又∵△ADE≌△CBF,∴∠ADE=∠CBF,∠AED=∠CFB.
∵∠EDF=∠ADC-∠ADE,∠FBE=∠CBA-∠CBF,∠AED+∠DEB=180°,∠CFB+∠BFD=180°,
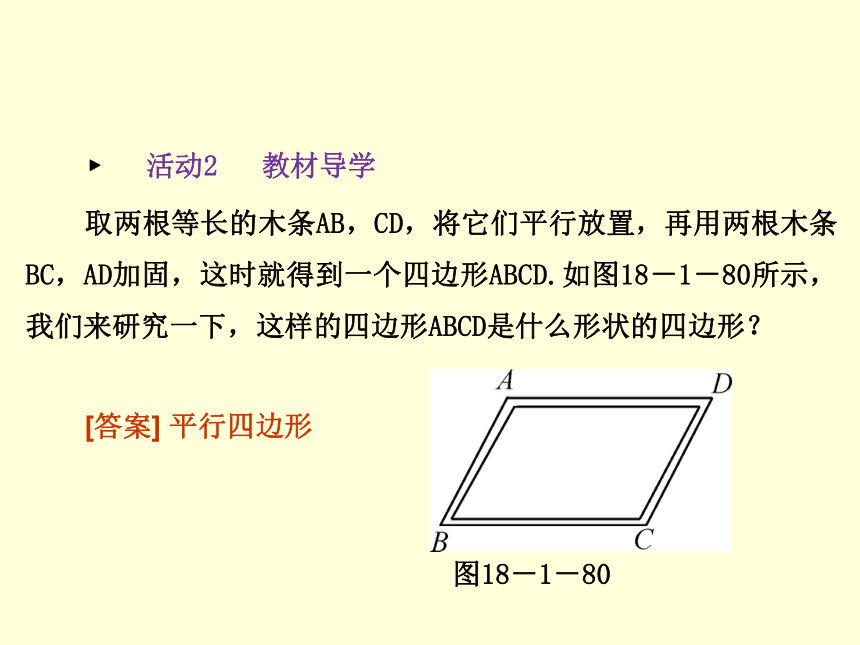
∴∠EDF=∠FBE,∠DEB=∠BFD,∴四边形EBFD是平行四边形. ? 活动1 知识准备第2课时 平行四边形的判定(2)如图18-1-79,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是____________________________________________________________________________________________________________.答案不唯一,如:AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等第2课时 平行四边形的判定(2)图18-1-79 ? 活动2 教材导学 第2课时 平行四边形的判定(2)取两根等长的木条AB,CD,将它们平行放置,再用两根木条BC,AD加固,这时就得到一个四边形ABCD.如图18-1-80所示,我们来研究一下,这样的四边形ABCD是什么形状的四边形?[答案] 平行四边形图18-1-80 ? 知识点一 由一组对边的位置和数量关系判定平行四边形 第2课时 平行四边形的判定(2)定理4:一组对边_______且______的四边形是平行四边形.
符号语言:如图18-1-81所示,在四边形ABCD中,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
[说明] 如果两条线段AB,CD既平行又相等,即AB∥CD且AB=CD,也可记作AB CD图18-1-81平行相等探究问题一 用一组对边的关系判定平行四边形 第2课时 平行四边形的判定(2)例1 如图18-1-82,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边三角形ACD,等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.由以上条件请你证明四边形ADFE是平行四边形. 图18-1-82[解析] 证明AD∥EF且AC=EF=AD即可.第2课时 平行四边形的判定(2)证明:易证AC=EF.
∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=60°+30°=90°.
又∵FE⊥AB,
∴∠EFA=90°=∠DAB,
∴AD∥EF .第2课时 平行四边形的判定(2)又∵AC=EF(已证),AC=AD,
∴AD=EF,
∴四边形ADFE是平行四边形.
[归纳总结] 证明一个四边形是平行四边形的方法较多,但在选择证明方法时,通常结合题目中的条件(含图形)进行分析,选择最简便的方法或最有效的方法.一般判定一个四边形是平行四边形的思路如下:第2课时 平行四边形的判定(2)第2课时 平行四边形的判定(2)探究问题二 平行四边形的性质与判定的综合运用 例2 如图18-1-83所示,在?ABCD中,AB>BC,∠A与∠D的平分线交于点E,∠B与∠C的平分线交于点F,连接EF.
(1)延长DE交AB于点M,则图中与线段EM一定相等的线段有哪几条?说明理由;(不再另外添加字母和辅助线)
(2)EF,BC与AB之间有怎样的数量关系?为什么?第2课时 平行四边形的判定(2)图18-1-83第2课时 平行四边形的判定(2)解:(1)图中与线段EM一定相等的线段有2条,ED和BF.
理由:∵四边形ABCD是平行四边形,
∴∠ADC+∠BAD=180°.
∵AE,DE分别平分∠DAB和∠ADC,
∴AE⊥DM,
∴△AED≌△AEM,
∴ED=EM.第2课时 平行四边形的判定(2)∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD.
∵AE,CF是∠DAB和∠BCD的平分线,
∴∠DAE=∠BCF.
同理∠ADE=∠CBF.
又∵AD=CB,
∴△ADE≌△CBF,第2课时 平行四边形的判定(2)∴DE=BF,
∴BF=EM.
(2)EF+BC=AB.
理由:由(1)易证∠AMD=∠ABF=∠ADM,
∴EM∥BF.由(1)得EM=BF,
∴四边形EFBM是平行四边形,
∴EF=MB,BC=AD=AM,
∴EF+BC=AB.第2课时 平行四边形的判定(2)[归纳总结] 在平行四边形的综合运用时,往往需要利用平行四边形的性质转化为全等三角形,再通过全等三角形的性质转化出判定平行四边形的条件.转化关系如下:第2课时 平行四边形的判定(2)同时,有关平行四边形的问题也有一些典型的模型,本例中就有两个典型的模型:
1.“平行线+角平分线”构造直角三角形.如图18-1-84所示,∠E=∠F=90°.图18-1-84第2课时 平行四边形的判定(2)2.“平行线+角平分线”构造等腰三角形,如图18-1-85所示,AD=AM.图18-1-85
如图18-1-78所示,在?ABCD中,E,F分别是AB,CD的中点.
(1)求证:△ADE≌△CBF;
(2)至少用三种方法证明四边形EBFD是平行四边形.图18-1-78图18-1-78第2课时 平行四边形的判定(2)第2课时 平行四边形的判定(2)第2课时 平行四边形的判定(2)方法三:∵四边形ABCD是平行四边形,∴∠ADC=∠CBA.
又∵△ADE≌△CBF,∴∠ADE=∠CBF,∠AED=∠CFB.
∵∠EDF=∠ADC-∠ADE,∠FBE=∠CBA-∠CBF,∠AED+∠DEB=180°,∠CFB+∠BFD=180°,
∴∠EDF=∠FBE,∠DEB=∠BFD,∴四边形EBFD是平行四边形. ? 活动1 知识准备第2课时 平行四边形的判定(2)如图18-1-79,在四边形ABCD中,AB∥CD,请你添加一个条件,使得四边形ABCD成为平行四边形,你添加的条件是____________________________________________________________________________________________________________.答案不唯一,如:AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等第2课时 平行四边形的判定(2)图18-1-79 ? 活动2 教材导学 第2课时 平行四边形的判定(2)取两根等长的木条AB,CD,将它们平行放置,再用两根木条BC,AD加固,这时就得到一个四边形ABCD.如图18-1-80所示,我们来研究一下,这样的四边形ABCD是什么形状的四边形?[答案] 平行四边形图18-1-80 ? 知识点一 由一组对边的位置和数量关系判定平行四边形 第2课时 平行四边形的判定(2)定理4:一组对边_______且______的四边形是平行四边形.
符号语言:如图18-1-81所示,在四边形ABCD中,
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形.
[说明] 如果两条线段AB,CD既平行又相等,即AB∥CD且AB=CD,也可记作AB CD图18-1-81平行相等探究问题一 用一组对边的关系判定平行四边形 第2课时 平行四边形的判定(2)例1 如图18-1-82,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边三角形ACD,等边三角形ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.由以上条件请你证明四边形ADFE是平行四边形. 图18-1-82[解析] 证明AD∥EF且AC=EF=AD即可.第2课时 平行四边形的判定(2)证明:易证AC=EF.
∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=60°+30°=90°.
又∵FE⊥AB,
∴∠EFA=90°=∠DAB,
∴AD∥EF .第2课时 平行四边形的判定(2)又∵AC=EF(已证),AC=AD,
∴AD=EF,
∴四边形ADFE是平行四边形.
[归纳总结] 证明一个四边形是平行四边形的方法较多,但在选择证明方法时,通常结合题目中的条件(含图形)进行分析,选择最简便的方法或最有效的方法.一般判定一个四边形是平行四边形的思路如下:第2课时 平行四边形的判定(2)第2课时 平行四边形的判定(2)探究问题二 平行四边形的性质与判定的综合运用 例2 如图18-1-83所示,在?ABCD中,AB>BC,∠A与∠D的平分线交于点E,∠B与∠C的平分线交于点F,连接EF.
(1)延长DE交AB于点M,则图中与线段EM一定相等的线段有哪几条?说明理由;(不再另外添加字母和辅助线)
(2)EF,BC与AB之间有怎样的数量关系?为什么?第2课时 平行四边形的判定(2)图18-1-83第2课时 平行四边形的判定(2)解:(1)图中与线段EM一定相等的线段有2条,ED和BF.
理由:∵四边形ABCD是平行四边形,
∴∠ADC+∠BAD=180°.
∵AE,DE分别平分∠DAB和∠ADC,
∴AE⊥DM,
∴△AED≌△AEM,
∴ED=EM.第2课时 平行四边形的判定(2)∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD.
∵AE,CF是∠DAB和∠BCD的平分线,
∴∠DAE=∠BCF.
同理∠ADE=∠CBF.
又∵AD=CB,
∴△ADE≌△CBF,第2课时 平行四边形的判定(2)∴DE=BF,
∴BF=EM.
(2)EF+BC=AB.
理由:由(1)易证∠AMD=∠ABF=∠ADM,
∴EM∥BF.由(1)得EM=BF,
∴四边形EFBM是平行四边形,
∴EF=MB,BC=AD=AM,
∴EF+BC=AB.第2课时 平行四边形的判定(2)[归纳总结] 在平行四边形的综合运用时,往往需要利用平行四边形的性质转化为全等三角形,再通过全等三角形的性质转化出判定平行四边形的条件.转化关系如下:第2课时 平行四边形的判定(2)同时,有关平行四边形的问题也有一些典型的模型,本例中就有两个典型的模型:
1.“平行线+角平分线”构造直角三角形.如图18-1-84所示,∠E=∠F=90°.图18-1-84第2课时 平行四边形的判定(2)2.“平行线+角平分线”构造等腰三角形,如图18-1-85所示,AD=AM.图18-1-85
