18.2.2菱形的性质第1课时
文档属性
| 名称 | 18.2.2菱形的性质第1课时 |  | |
| 格式 | zip | ||
| 文件大小 | 487.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 09:06:38 | ||
图片预览






文档简介
课件20张PPT。数 学新课标(RJ) 八年级下册第十八章 平行四边形18.2 特殊的平行四边形18.2.2 菱形第1课时 菱形的性质探 究 新 知 ? 活动1 知识准备第1课时 菱形的性质1.矩形的性质与一般平行四边形的性质的区别主要表现在____和__________两个方面,其判定也主要从这两个方面来寻求条件.
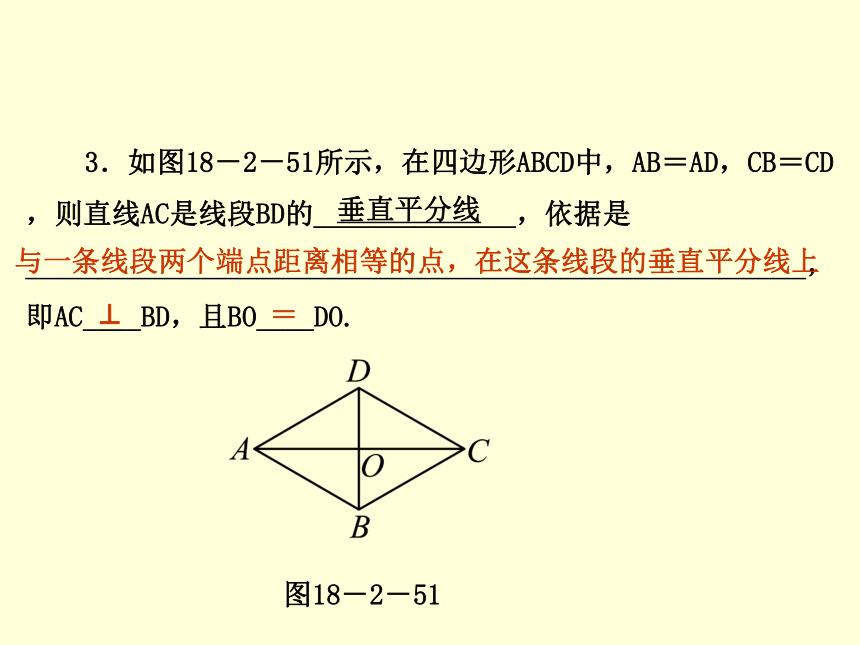
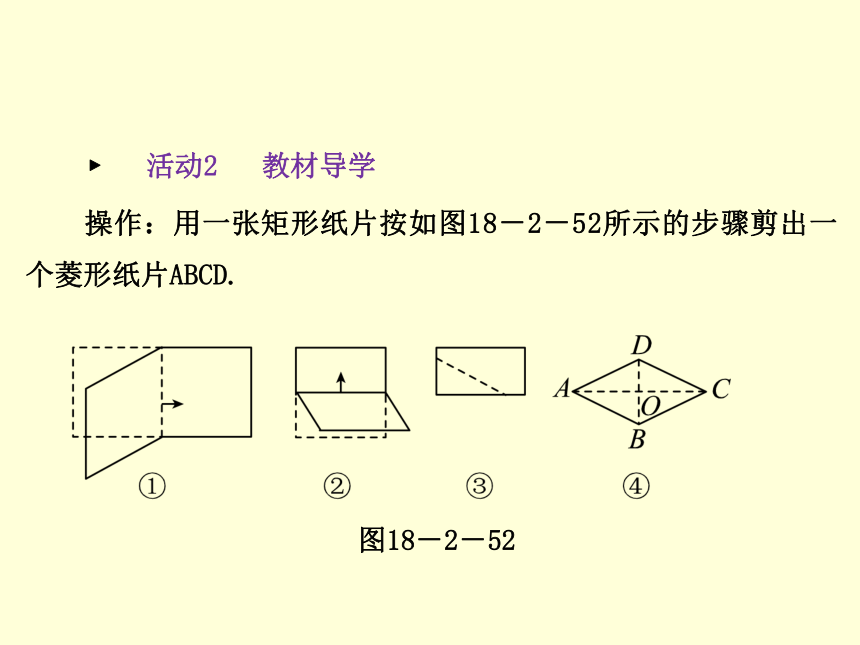
2.在等腰三角形中,______________、________________、_____________________线三线合一.角对角线顶角的平分线底边上的高线底边上的中第1课时 菱形的性质3.如图18-2-51所示,在四边形ABCD中,AB=AD,CB=CD,则直线AC是线段BD的______________,依据是______________________________________________________,即AC____BD,且BO____DO.图18-2-51垂直平分线与一条线段两个端点距离相等的点,在这条线段的垂直平分线上⊥= ? 活动2 教材导学 第1课时 菱形的性质操作:用一张矩形纸片按如图18-2-52所示的步骤剪出一个菱形纸片ABCD.图18-2-52第1课时 菱形的性质通过上面的操作过程,你的发现有:
(1)菱形ABCD的边:AB____BC____CD____DA(用“=”或“≠”填空),即___________________________;
(2)菱形的两条对角线把菱形分成四个______的直角三角形,所以菱形的面积还可以转化成一个______三角形面积的____倍;===菱形的四条边都相等全等直角4第1课时 菱形的性质(3)菱形ABCD的对角线AC____BD,∠DAO____∠BAO____∠DCO____∠BCO,∠ABO____∠CBO____∠ADO____∠CDO,即______________________________________________________;
(4)菱形ABCD是________图形,它的_________所在的直线是它的对称轴.⊥======菱形的两条对角线互相垂直,并且每一条对角线平分一组对角轴对称对角线新 知 梳 理 ? 知识点一 菱形的概念 第1课时 菱形的性质定义:有一组邻边_______的平行四边形叫做菱形.
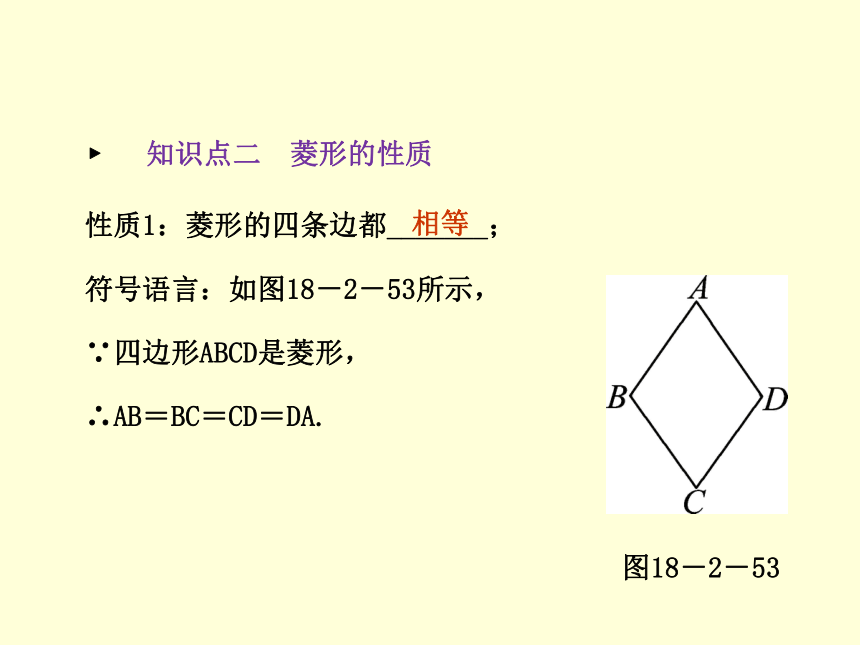
菱形是特殊的平行四边形,它是轴对称图形,对角线所在的直线就是它的对称轴.菱形满足的两个条件:一是平行四边形,二是一组邻边相等,二者缺一不可.相等第1课时 菱形的性质 ? 知识点二 菱形的性质 性质1:菱形的四条边都_______;
符号语言:如图18-2-53所示,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.图18-2-53相等第1课时 菱形的性质性质2:菱形的两条对角线________________,并且每一条对角线平分_____________.
符号语言:如图18-2-54所示,互相垂直一组对角图18-2-54第1课时 菱形的性质∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∠ABD=∠CBD,∠ADB=∠CDB,∠BAC=∠DAC,∠BCA=∠DCA. 第1课时 菱形的性质 ? 知识点三 菱形的面积 公式:(1)菱形的面积等于底×高.
(2)菱形的面积等于两条对角线__________________.乘积的一半重难互动探究探究问题一 利用菱形的性质进行计算第1课时 菱形的性质例1 如图18-2-55,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过点O作OE⊥AB,垂足为E.
(1)求∠ABD的度数;
(2)求线段BE的长.图18-2-55第1课时 菱形的性质解:(1)在菱形ABCD中,AB=AD,∠A=60°,
∴△ABD为等边三角形,
∴∠ABD=60°.
(2)由(1)可知BD=AB=4.
又∵O为BD的中点,
∴OB=2.
又∵OE⊥AB,∠ABD=60°,
∴∠BOE=30°,
∴BE=1.第1课时 菱形的性质[归纳总结] 菱形的四条边都相等,如果菱形中出现“30°”“60°”“120°”“一边等于最短的对角线”这些词语时,那么可得出等边三角形.又因为菱形的对角线互相垂直,所以还往往用到勾股定理.第1课时 菱形的性质探究问题二 利用菱形的性质进行证明 例2 如图18-2-56所示,菱形ABCD中,E,F分别是BC,CD上的点,且BE=DF.
(1)求证:AE=AF;
(2)若∠B=60°,点E,F分别为BC,CD的中点,求证:△AEF为等边三角形.图18-2-56第1课时 菱形的性质[解析] (1)证明△ABE≌△ADF.
(2)连接AC,△ABC是等边三角形,E是BC的中点,∴∠CAE=30°,同理∠CAF=30°,∴∠EAF=60°,即可证△AEF为等边三角形.第1课时 菱形的性质证明:(1)∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
又∵BE=DF,
∴△ABE≌△ADF,
∴AE=AF.图18-2-57第1课时 菱形的性质(2)连接AC,如图18-2-57所示.
∵AB=BC,∠B=60°,
∴△ABC是等边三角形.
又∵E是BC的中点,
∴AE⊥BC,
∴∠CAE=30°.
同理∠CAF=30°,
∴∠EAF=∠CAE+∠CAF=60°.
又∵AE=AF,
∴△AEF是等边三角形.第1课时 菱形的性质[归纳总结] 菱形的每条对角线把菱形分成两个全等的等腰三角形,两条对角线把菱形分成四个全等的直角三角形,所以有关菱形的一些证明或计算问题常可以应用等腰三角形或直角三角形的知识来解决.
2.在等腰三角形中,______________、________________、_____________________线三线合一.角对角线顶角的平分线底边上的高线底边上的中第1课时 菱形的性质3.如图18-2-51所示,在四边形ABCD中,AB=AD,CB=CD,则直线AC是线段BD的______________,依据是______________________________________________________,即AC____BD,且BO____DO.图18-2-51垂直平分线与一条线段两个端点距离相等的点,在这条线段的垂直平分线上⊥= ? 活动2 教材导学 第1课时 菱形的性质操作:用一张矩形纸片按如图18-2-52所示的步骤剪出一个菱形纸片ABCD.图18-2-52第1课时 菱形的性质通过上面的操作过程,你的发现有:
(1)菱形ABCD的边:AB____BC____CD____DA(用“=”或“≠”填空),即___________________________;
(2)菱形的两条对角线把菱形分成四个______的直角三角形,所以菱形的面积还可以转化成一个______三角形面积的____倍;===菱形的四条边都相等全等直角4第1课时 菱形的性质(3)菱形ABCD的对角线AC____BD,∠DAO____∠BAO____∠DCO____∠BCO,∠ABO____∠CBO____∠ADO____∠CDO,即______________________________________________________;
(4)菱形ABCD是________图形,它的_________所在的直线是它的对称轴.⊥======菱形的两条对角线互相垂直,并且每一条对角线平分一组对角轴对称对角线新 知 梳 理 ? 知识点一 菱形的概念 第1课时 菱形的性质定义:有一组邻边_______的平行四边形叫做菱形.
菱形是特殊的平行四边形,它是轴对称图形,对角线所在的直线就是它的对称轴.菱形满足的两个条件:一是平行四边形,二是一组邻边相等,二者缺一不可.相等第1课时 菱形的性质 ? 知识点二 菱形的性质 性质1:菱形的四条边都_______;
符号语言:如图18-2-53所示,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA.图18-2-53相等第1课时 菱形的性质性质2:菱形的两条对角线________________,并且每一条对角线平分_____________.
符号语言:如图18-2-54所示,互相垂直一组对角图18-2-54第1课时 菱形的性质∵四边形ABCD是菱形,
∴AC⊥BD,AO=CO,BO=DO,
∠ABD=∠CBD,∠ADB=∠CDB,∠BAC=∠DAC,∠BCA=∠DCA. 第1课时 菱形的性质 ? 知识点三 菱形的面积 公式:(1)菱形的面积等于底×高.
(2)菱形的面积等于两条对角线__________________.乘积的一半重难互动探究探究问题一 利用菱形的性质进行计算第1课时 菱形的性质例1 如图18-2-55,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过点O作OE⊥AB,垂足为E.
(1)求∠ABD的度数;
(2)求线段BE的长.图18-2-55第1课时 菱形的性质解:(1)在菱形ABCD中,AB=AD,∠A=60°,
∴△ABD为等边三角形,
∴∠ABD=60°.
(2)由(1)可知BD=AB=4.
又∵O为BD的中点,
∴OB=2.
又∵OE⊥AB,∠ABD=60°,
∴∠BOE=30°,
∴BE=1.第1课时 菱形的性质[归纳总结] 菱形的四条边都相等,如果菱形中出现“30°”“60°”“120°”“一边等于最短的对角线”这些词语时,那么可得出等边三角形.又因为菱形的对角线互相垂直,所以还往往用到勾股定理.第1课时 菱形的性质探究问题二 利用菱形的性质进行证明 例2 如图18-2-56所示,菱形ABCD中,E,F分别是BC,CD上的点,且BE=DF.
(1)求证:AE=AF;
(2)若∠B=60°,点E,F分别为BC,CD的中点,求证:△AEF为等边三角形.图18-2-56第1课时 菱形的性质[解析] (1)证明△ABE≌△ADF.
(2)连接AC,△ABC是等边三角形,E是BC的中点,∴∠CAE=30°,同理∠CAF=30°,∴∠EAF=60°,即可证△AEF为等边三角形.第1课时 菱形的性质证明:(1)∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D.
又∵BE=DF,
∴△ABE≌△ADF,
∴AE=AF.图18-2-57第1课时 菱形的性质(2)连接AC,如图18-2-57所示.
∵AB=BC,∠B=60°,
∴△ABC是等边三角形.
又∵E是BC的中点,
∴AE⊥BC,
∴∠CAE=30°.
同理∠CAF=30°,
∴∠EAF=∠CAE+∠CAF=60°.
又∵AE=AF,
∴△AEF是等边三角形.第1课时 菱形的性质[归纳总结] 菱形的每条对角线把菱形分成两个全等的等腰三角形,两条对角线把菱形分成四个全等的直角三角形,所以有关菱形的一些证明或计算问题常可以应用等腰三角形或直角三角形的知识来解决.
