18.1.1平行四边形的性质(第2课时)
文档属性
| 名称 | 18.1.1平行四边形的性质(第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 797.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-04-28 09:06:17 | ||
图片预览




文档简介
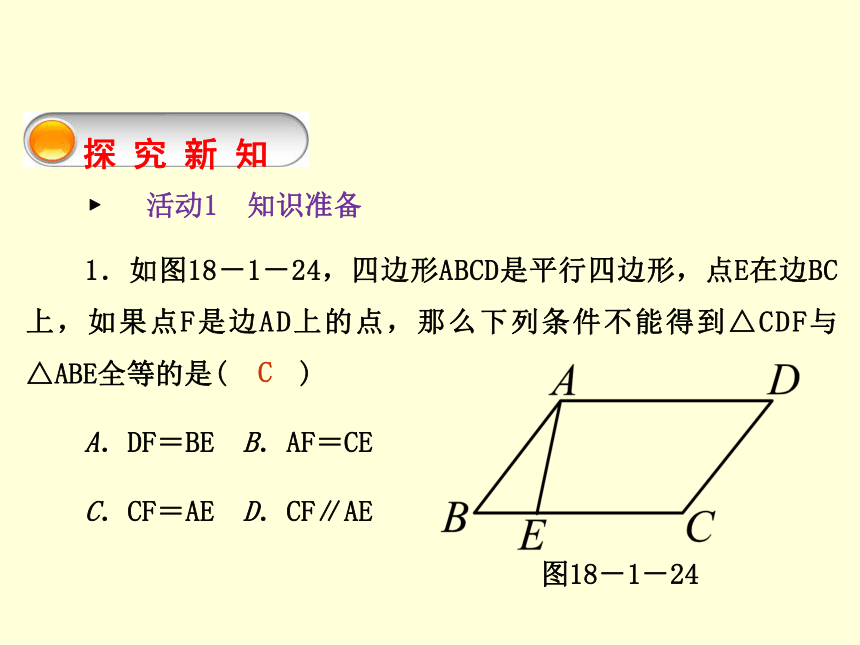
课件14张PPT。数 学新课标(RJ) 八年级下册第十八章 平行四边形 18.1 平行四边形18.1.1 平行四边形的性质第2课时 平行四边形的性质(2)探 究 新 知 ? 活动1 知识准备第2课时 平行四边形的性质(2)1.如图18-1-24,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么下列条件不能得到△CDF与△ABE全等的是( )
A.DF=BE B.AF=CE
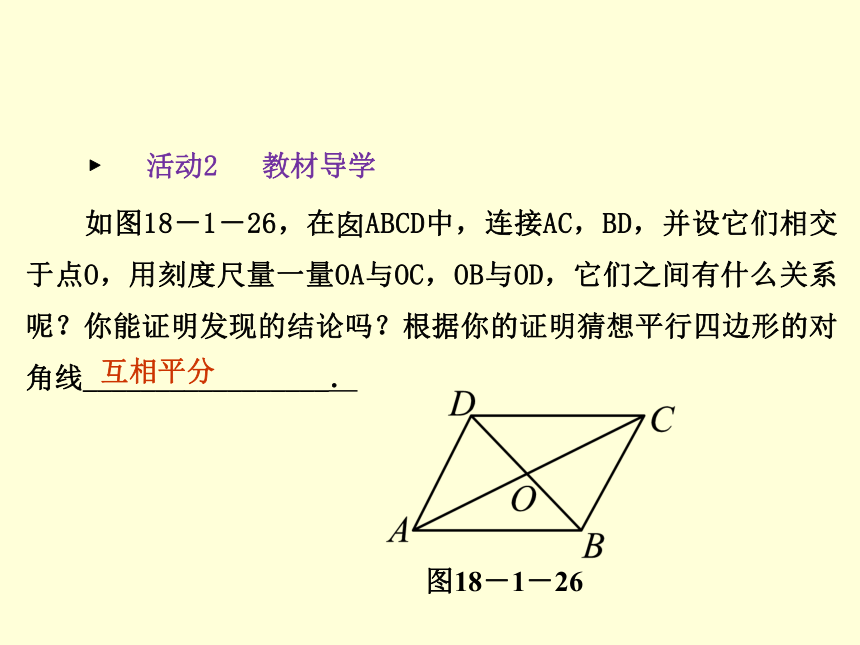
C.CF=AE D.CF∥AE图18-1-24C第2课时 平行四边形的性质(2)2.如图18-1-25所示,l1∥l2,BE∥CF,BA⊥l1,DC⊥l2,下面给出四个结论:①AB=CD;②BE=CF;③S△ABE=S△DCF;④S?ABCD=S?BCFE.其中正确的结论是___________(填序号).①②③④图18-1-25 ? 活动2 教材导学 第2课时 平行四边形的性质(2)如图18-1-26,在?ABCD中,连接AC,BD,并设它们相交于点O,用刻度尺量一量OA与OC,OB与OD,它们之间有什么关系呢?你能证明发现的结论吗?根据你的证明猜想平行四边形的对角线_________________.图18-1-26互相平分第2课时 平行四边形的性质(2)[答案] OA=OC,OB=OD.证明如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠DCO=∠BAO,∠CDO=∠ABO,
∴△ABO≌△CDO,
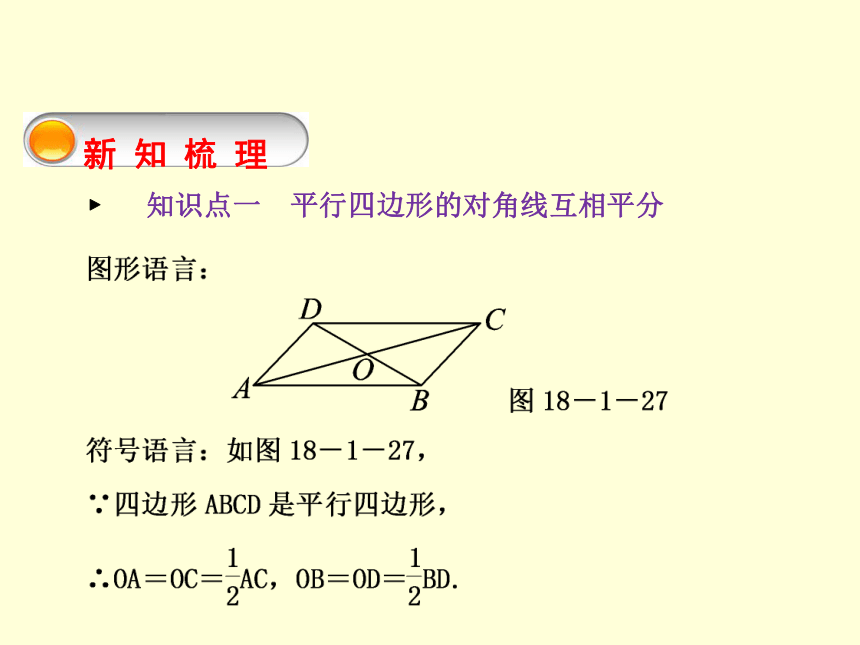
∴OA=OC,OB=OD.新 知 梳 理 ? 知识点一 平行四边形的对角线互相平分 第2课时 平行四边形的性质(2)重难互动探究探究问题一 平行四边形对角线性质定理的运用 第2课时 平行四边形的性质(2)例1 如图18-1-28所示,已知?ABCD和?EBFD,点A,E,F,C在一条直线上.
求证:AE=CF.图18-1-28第2课时 平行四边形的性质(2)[解析] 要证AE=CF,用我们熟知的三角形全等可以证明,但由于题设中有两个平行四边形,所以我们也可以利用平行四边形的性质来证明.第2课时 平行四边形的性质(2)证明:如图18-1-28,连接BD,交AC于点O.
∵四边形ABCD,四边形EBFD是平行四边形,
∴AO=CO,EO=FO,
∴AO-EO=CO-FO,
∴AE=CF.
[归纳总结] 在解证平行四边形的有关问题时,除可以考虑证明三角形全等以外,更应注意运用平行四边形的性质.连接对角线是平行四边形中常作的辅助线.第2课时 平行四边形的性质(2)探究问题二 平行四边形性质的综合运用 例2 如图18-1-29,在?ABCD中,AC,BD相交于点O,点E,A,C,F在同一条直线上,∠E=∠F.
求证:∠ABE=∠CDF.图18-1-29第2课时 平行四边形的性质(2)[解析] 由平行四边形对角线的性质可得OB=OD,可根据AAS得到△OBE≌△ODF,在得到∠OBE=∠ODF后,再结合由AB∥CD得到的∠ABO=∠CDO可得结论.第2课时 平行四边形的性质(2)证明:∵在?ABCD中,AC,BD相交于O,
∴OB=OD,AB∥CD.
在△OBE与△ODF中,
∵∠BOE=∠DOF,∠E=∠F,OB=OD,
∴△OBE≌△ODF,
∴∠OBE=∠ODF.
∵AB∥CD,第2课时 平行四边形的性质(2)∴∠ABO=∠CDO,
∴∠OBE-∠ABO =∠ODF-∠CDO,
∴∠ABE=∠CDF.
[归纳总结] 平行四边形的性质提供了边的平行与相等、角的相等与互补、对角线的互相平分,当所给条件在对角线上时,往往利用平行四边形的对角线互相平分这一性质.
A.DF=BE B.AF=CE
C.CF=AE D.CF∥AE图18-1-24C第2课时 平行四边形的性质(2)2.如图18-1-25所示,l1∥l2,BE∥CF,BA⊥l1,DC⊥l2,下面给出四个结论:①AB=CD;②BE=CF;③S△ABE=S△DCF;④S?ABCD=S?BCFE.其中正确的结论是___________(填序号).①②③④图18-1-25 ? 活动2 教材导学 第2课时 平行四边形的性质(2)如图18-1-26,在?ABCD中,连接AC,BD,并设它们相交于点O,用刻度尺量一量OA与OC,OB与OD,它们之间有什么关系呢?你能证明发现的结论吗?根据你的证明猜想平行四边形的对角线_________________.图18-1-26互相平分第2课时 平行四边形的性质(2)[答案] OA=OC,OB=OD.证明如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠DCO=∠BAO,∠CDO=∠ABO,
∴△ABO≌△CDO,
∴OA=OC,OB=OD.新 知 梳 理 ? 知识点一 平行四边形的对角线互相平分 第2课时 平行四边形的性质(2)重难互动探究探究问题一 平行四边形对角线性质定理的运用 第2课时 平行四边形的性质(2)例1 如图18-1-28所示,已知?ABCD和?EBFD,点A,E,F,C在一条直线上.
求证:AE=CF.图18-1-28第2课时 平行四边形的性质(2)[解析] 要证AE=CF,用我们熟知的三角形全等可以证明,但由于题设中有两个平行四边形,所以我们也可以利用平行四边形的性质来证明.第2课时 平行四边形的性质(2)证明:如图18-1-28,连接BD,交AC于点O.
∵四边形ABCD,四边形EBFD是平行四边形,
∴AO=CO,EO=FO,
∴AO-EO=CO-FO,
∴AE=CF.
[归纳总结] 在解证平行四边形的有关问题时,除可以考虑证明三角形全等以外,更应注意运用平行四边形的性质.连接对角线是平行四边形中常作的辅助线.第2课时 平行四边形的性质(2)探究问题二 平行四边形性质的综合运用 例2 如图18-1-29,在?ABCD中,AC,BD相交于点O,点E,A,C,F在同一条直线上,∠E=∠F.
求证:∠ABE=∠CDF.图18-1-29第2课时 平行四边形的性质(2)[解析] 由平行四边形对角线的性质可得OB=OD,可根据AAS得到△OBE≌△ODF,在得到∠OBE=∠ODF后,再结合由AB∥CD得到的∠ABO=∠CDO可得结论.第2课时 平行四边形的性质(2)证明:∵在?ABCD中,AC,BD相交于O,
∴OB=OD,AB∥CD.
在△OBE与△ODF中,
∵∠BOE=∠DOF,∠E=∠F,OB=OD,
∴△OBE≌△ODF,
∴∠OBE=∠ODF.
∵AB∥CD,第2课时 平行四边形的性质(2)∴∠ABO=∠CDO,
∴∠OBE-∠ABO =∠ODF-∠CDO,
∴∠ABE=∠CDF.
[归纳总结] 平行四边形的性质提供了边的平行与相等、角的相等与互补、对角线的互相平分,当所给条件在对角线上时,往往利用平行四边形的对角线互相平分这一性质.
